Python数据分析-股票分析和可视化(深证指数)
一、内容简介
股市指数作为衡量股市整体表现的重要工具,不仅反映了市场的即时状态,也提供了经济健康状况的关键信号。在全球经济体系中,股市指数被广泛用于预测经济活动,评估投资环境,以及制定财政和货币政策。在中国,深证指数作为深圳证券交易所的主要指数之一,它包含了深市的所有上市公司,因此能够全面地反映中国改革开放后经济发展的成果以及区域经济的活跃度。通过分析深证指数,可以得到中国经济特别是南方经济的宏观走向,这对投资者和政策制定者而言具有重要意义。
本项目采用了2022年的深证指数数据,主要目的是通过数据分析工具对该数据集进行深入分析和可视化。
二、问题讨论
数据清洗与预处理
数据加载:首先,使用Pandas的read_csv函数加载CSV格式的数据文件。
日期格式转换:将trade_date列中的日期字符串转换为Pandas的datetime对象,这是时间序列分析的重要步骤,因为它允许使用日期作为索引进行高效操作。
缺失值处理:检查数据中是否存在缺失值,如果存在,使用前向填充法(ffill)。这种方法假设数据的连续性,即前一个时间点的观察可以代替缺失值。
读取数据
数据和代码
报告代码数据
# 加载数据
file_path = 'sz_index_2022.csv'
if os.path.exists(file_path):df = pd.read_csv(file_path)
else:sys.exit("File not found.") 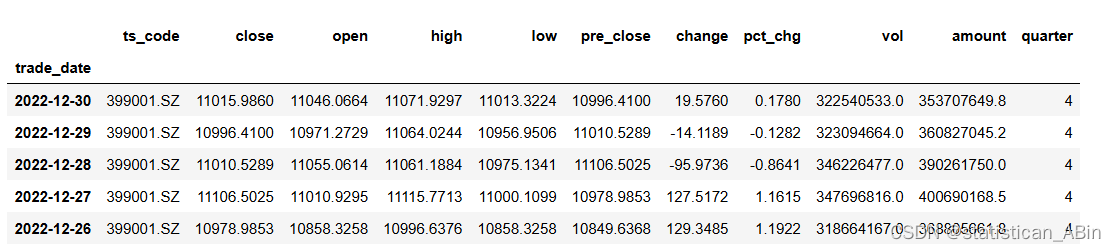
描述性统计分析
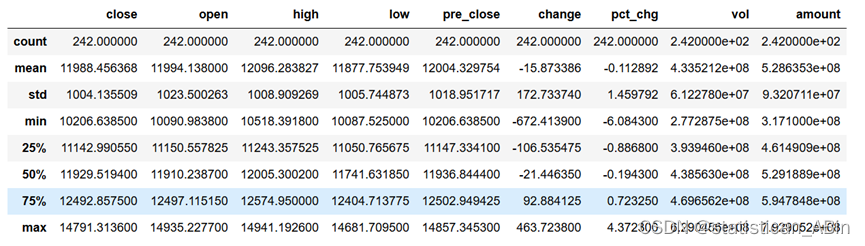
这些描述性统计结果展示了242个观测值的金融指标总结。具体来说,收盘价的平均值为11988.456368,标准差为1004.135569,最低值为10206.638500,最高值为14791.313600。开盘价的平均值为11994.138000,标准差为1023.500263,最低值为10090.983800,最高值为14935.227700。
接下来进行可视化
plt.figure(figsize=(10, 5))
plt.plot(df.index, df['close'], label='Closing Price') # 绘制收盘价折线图
plt.title('Shenzhen Index 2022 Closing Prices') # 设置标题
plt.xlabel('Date') # 设置X轴标签
plt.ylabel('Closing Price') # 设置Y轴标签
plt.legend()
plt.show()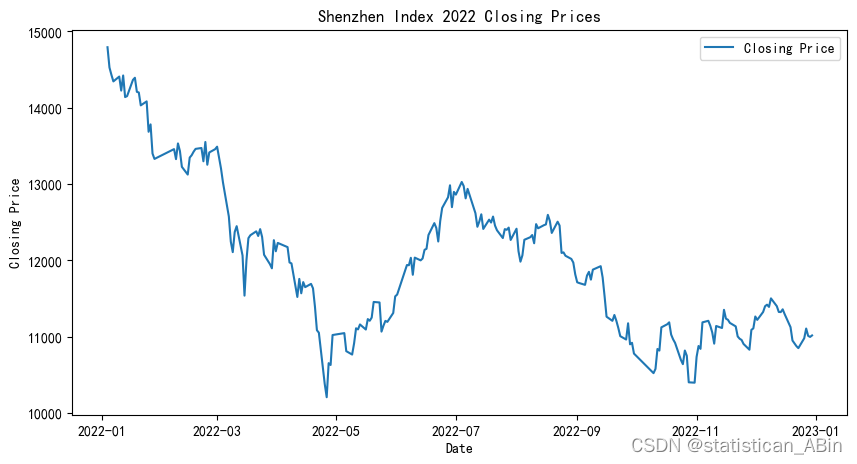
这个图表展示了2022年深圳指数的收盘价走势。从图中可以看出,整个2022年深圳指数经历了较大的波动:年初至3月,指数从约15000点大幅下跌至约12000点,显示出市场在这一段时间内表现较为疲软。
plt.figure(figsize=(10, 5))
plt.boxplot([df['open'], df['high'], df['low'], df['close']], labels=['Open', 'High', 'Low', 'Close']) # 绘制箱线图
plt.title('Box Plot of Opening, Highest, Lowest, and Closing Prices') # 设置标题
plt.show()

这个箱线图展示了2022年深圳指数的开盘价、最高价、最低价和收盘价的分布情况。从图中可以看出,开盘价(Open),中位数接近12000点,数据分布较为对称,范围从约10000点到14900点。上方存在一些离群值,表示有几天的开盘价异常高。。。
条形图用于展示不同类别数据的比较。我们绘制了开盘价、最高价、最低价和收盘价的平均值条形图。
avg_prices = [summary_stats[col]['mean'] for col in ['open', 'high', 'low', 'close']]
plt.figure(figsize=(10, 5))
plt.bar(['Open', 'High', 'Low', 'Close'], avg_prices, color=['blue', 'green', 'red', 'orange']) # 绘制条形图
plt.title('Average Prices') # 设置标题
plt.xlabel('Price Type') # 设置X轴标签
plt.ylabel('Average Price') # 设置Y轴标签
plt.show()
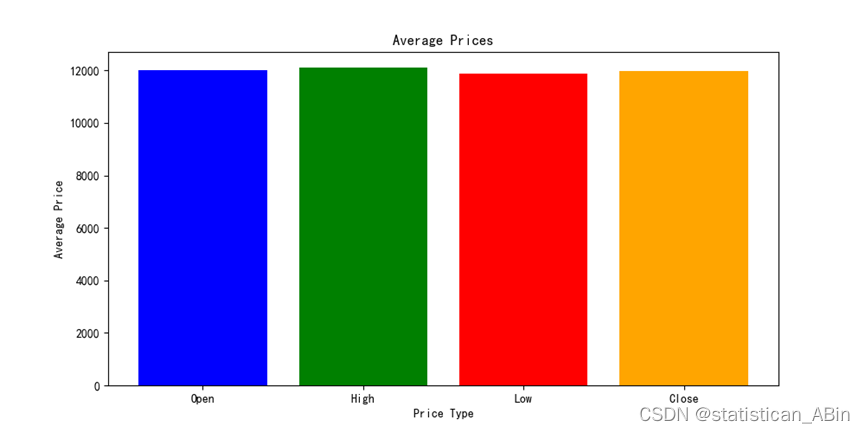
这个条形图展示了开盘价、最高价、最低价和收盘价的平均值。每个价格类型都用不同颜色的条形表示:开盘价(Open)平均开盘价接近12000点。说明市场在开盘时的价格大致稳定在这一水平。
直方图展示了数据的分布情况。我们绘制了2022年深圳指数收盘价的直方图。
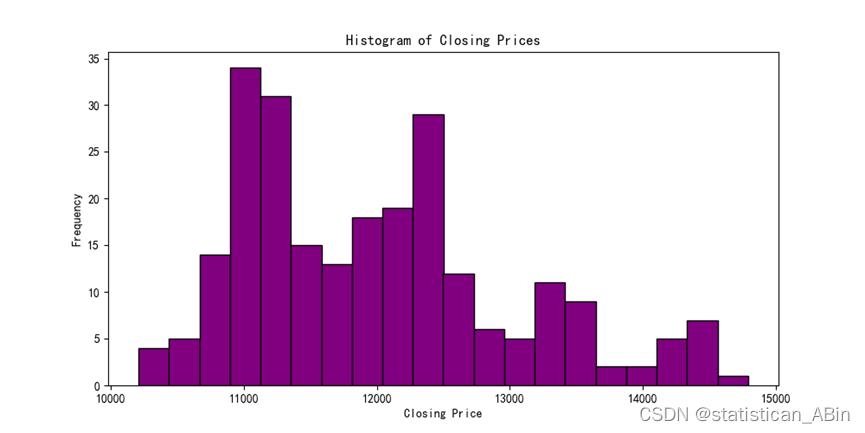
这个直方图展示了2022年深圳指数收盘价的分布情况。收盘价主要集中在11000点到13000点之间。在11000点到12000点之间的频率最高,显示出这一范围内的收盘价出现次数最多。
饼图用于展示各部分占总体的比例。我们绘制了2022年每个季度交易量占全年总交易量的比例。
df['quarter'] = df.index.quarter
volume_by_quarter = df.groupby('quarter')['vol'].sum() # 计算每季度总成交量
plt.figure(figsize=(10, 5))
plt.pie(volume_by_quarter, labels=['Q1', 'Q2', 'Q3', 'Q4'], autopct='%1.1f%%',colors=['gold', 'yellowgreen', 'lightcoral', 'lightskyblue']) # 绘制饼图
plt.title('Proportion of Total Trading Volume by Quarter') # 设置标题
plt.show()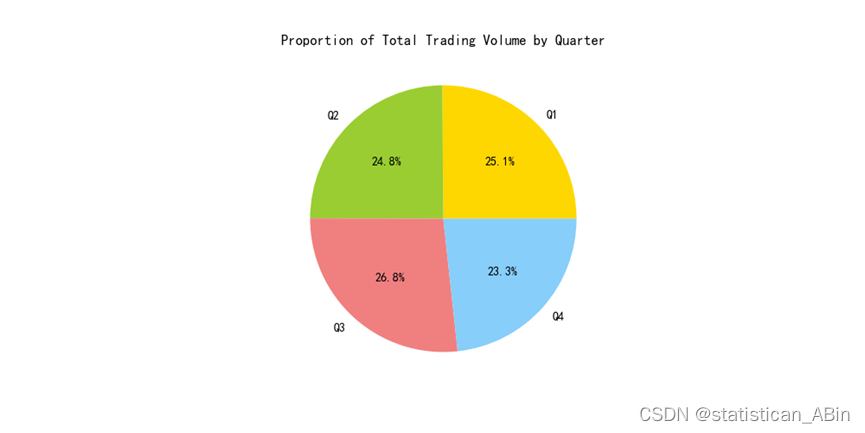
其中第一季度占比为25.1%,是全年交易量最高的季度。这一比例表明第一季度的市场交易活动较为活跃。第二季度占比为24.8%,略低于第一季度。这一比例显示第二季度的交易量与第一季度相当,市场活跃度持续。。。
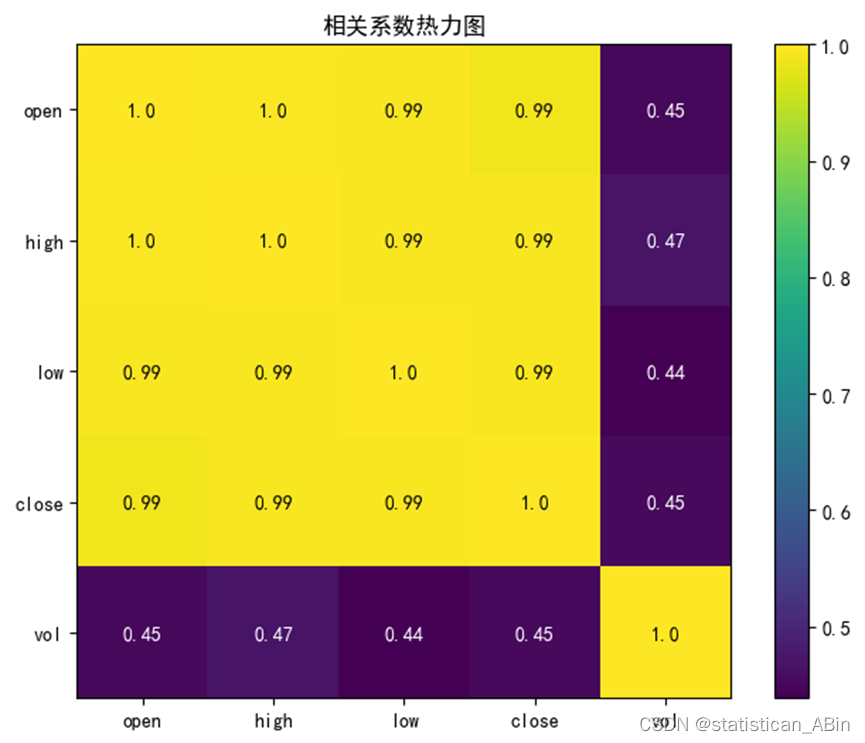
接下来计算相关矩阵 绘制散点图
# 计算相关矩阵
correlation_matrix = df[['open', 'high', 'low', 'close', 'vol', 'amount']].corr()
print("Correlation matrix:\n", correlation_matrix)# 绘制散点图
plt.figure(figsize=(12, 8))
for i, predictor in enumerate(['open', 'high', 'low', 'vol', 'amount']):plt.subplot(2, 3, i + 1)plt.scatter(df[predictor], df['close'], alpha=0.5)plt.xlabel(predictor)plt.ylabel('Close')
plt.tight_layout()
plt.show()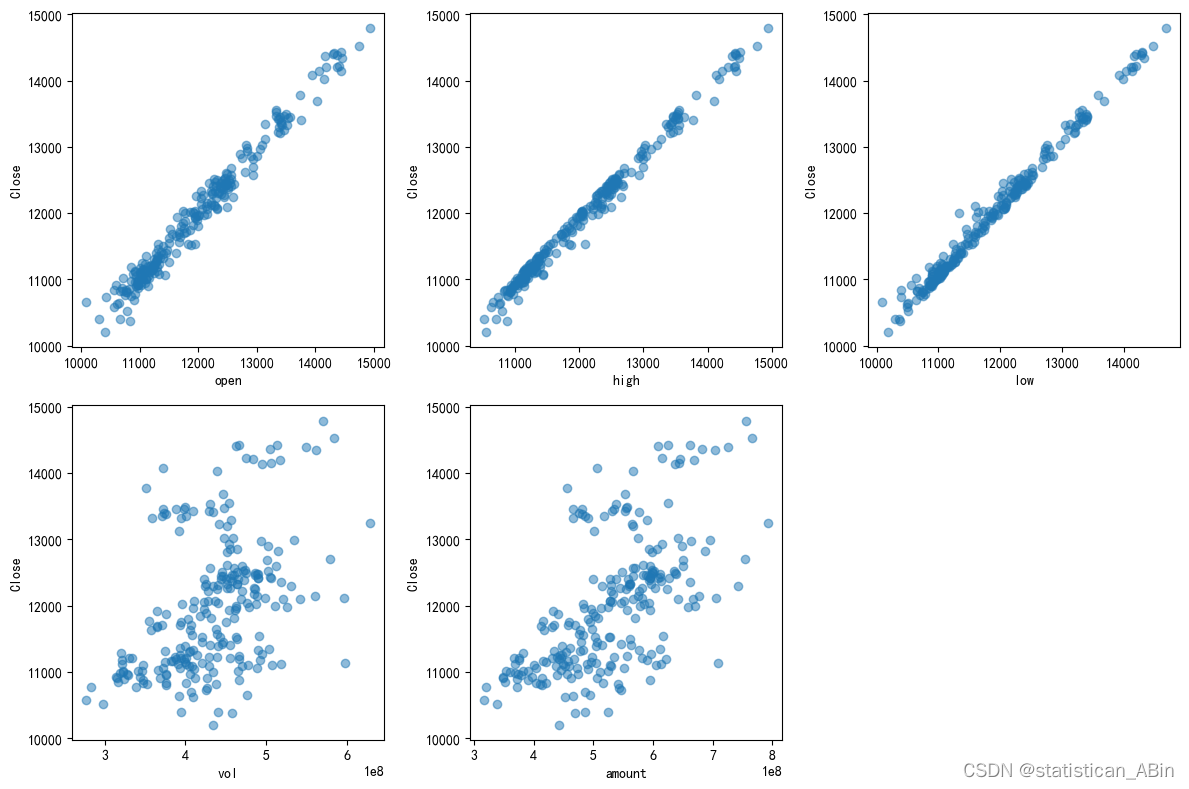
从图中可以看到,收盘价与开盘价、最高价、最低价之间有很强的线性关系,点几乎沿对角线分布。这表明这些特征之间有高度相关性。而收盘价与交易量和交易金额之间的相关性较低,点的分布较为分散。
 接下来线性回归分析
接下来线性回归分析
多元线性回归:建立以开盘价、最高价和最低价为自变量,收盘价为因变量的回归模型。计算并报告每个变量的系数,评估模型的效力和各变量的影响力。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
predictors = ['open', 'high', 'low', 'vol', 'amount']
X = df[predictors].values
y = df['close'].values
# 增加一个截距列
X = np.column_stack((np.ones(X.shape[0]), X))# 计算回归系数 (beta)
# beta = (X^T * X)^-1 * X^T * y
X_transpose = X.T
beta = np.linalg.inv(X_transpose @ X) @ X_transpose @ y# 计算预测值
y_pred = X @ beta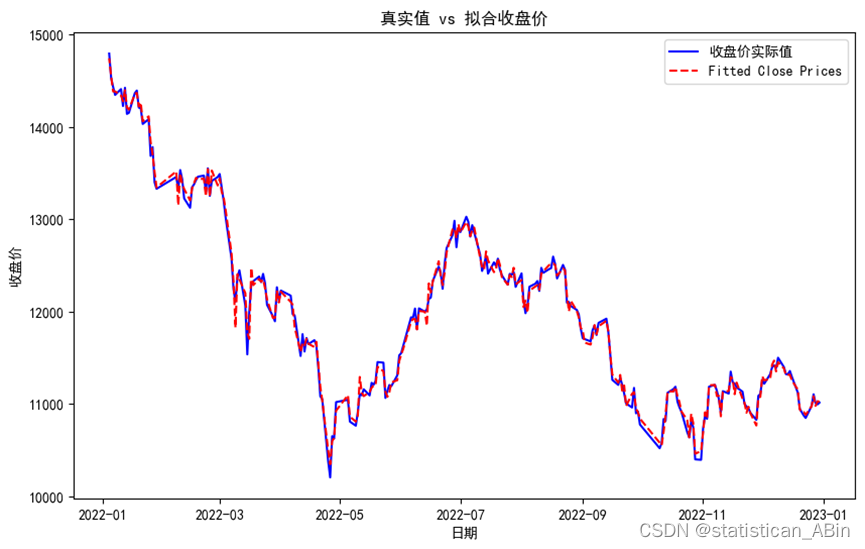
图中红色虚线(拟合收盘价)与蓝色实线(实际收盘价)基本重合,这表明模型对收盘价的预测非常准确。在大多数时间段内,拟合值与实际值的波动趋势基本一致。
三、结论
通过对2022年深证指数数据的综合分析,我们得出了以下主要结论:
在数据清洗与预处理方面,我们对数据进行了日期格式转换和缺失值处理,确保了分析的准确性和数据的连续性。这些步骤为后续的时间序列分析和可视化提供了可靠的基础。在描述性统计分析方面,通过计算开盘价、最高价、最低价和收盘价等主要金融指标的平均值、标准差、最大值和最小值,我们对市场的波动情况和价格分布有了基本了解。。。。
创作不易,希望大家多点赞关注评论!!!(类似代码或报告定制可以私信)
相关文章:

Python数据分析-股票分析和可视化(深证指数)
一、内容简介 股市指数作为衡量股市整体表现的重要工具,不仅反映了市场的即时状态,也提供了经济健康状况的关键信号。在全球经济体系中,股市指数被广泛用于预测经济活动,评估投资环境,以及制定财政和货币政策。在中国…...
Linux如何安装openjdk1.8
文章目录 Centosyum安装jdk和JRE配置全局环境变量验证ubuntu使用APT(适用于Ubuntu 16.04及以上版本)使用PPA(可选,适用于需要特定版本或旧版Ubuntu)Centos yum安装jdk和JRE yum install java-1.8.0-openjdk-devel.x86_64 安装后的目录 配置全局环境变量 vim /etc/pr…...

【LLVM】LTO学习
看这篇文章,文中的代码都是错的,给出的命令行也是错的。 真不如参考文献中也是华为的外国员工写的PPT。 但是,上述的文件中的指令也存在报错,还是官方文档看着舒服。...
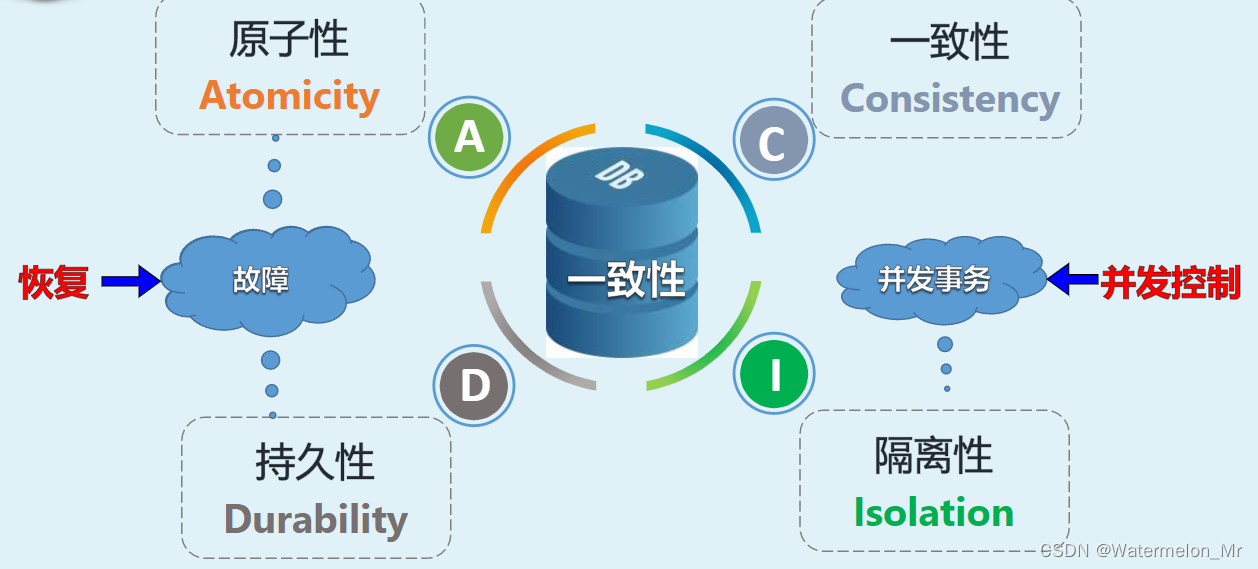
事务的特性-原子性(Atomicity)、一致性(Consistency)、隔离性(Asolation)、持久性(Durability)
一、引言 1、数据库管理系统DBMS为保证定义的事务是一个逻辑工作单元,达到引入事务的目的,实现的事务机制要保证事务具有原子性、一致性、隔离性和持久性,事务的这四个特性也统称为事务的ACID特性 2、当事务保持了ACID特性,才能…...
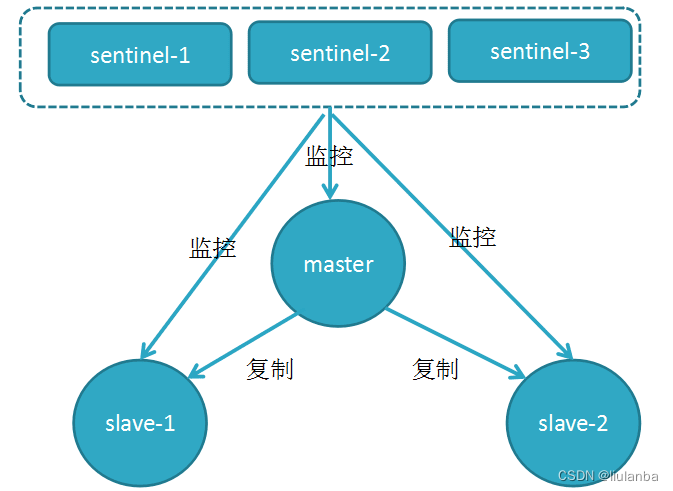
redis哨兵模式(Redis Sentinel)
哨兵模式的背景 当主服务器宕机后,需要手动把一台从服务器切换为主服务器,这就需要人工干预,费事费力,还会造成一段时间内服务不可用。这不是一种推荐的方式。 为了解决单点故障和提高系统的可用性,需要一种自动化的监…...

【牛客】牛客小白月赛97 题解 A - E
文章目录 A - 三角形B - 好数组C - 前缀平方和序列D - 走一个大整数迷宫E - 前缀和前缀最大值 A - 三角形 map存一下每个数出现了多少次,再遍历map #include <bits/stdc.h>using namespace std;#define int long long using i64 long long;typedef pair<…...

Spring Boot中泛型参数的灵活运用:最佳实践与性能优化
泛型是Java中一种强大的特性,它提供了编写通用代码的能力,使得代码更加灵活和可复用。在Spring Boot应用程序中,泛型参数的灵活运用可以带来诸多好处,包括增强代码的可读性、提高系统的健壮性以及优化系统的性能。本文将深入探讨在…...

MySQL建表时的注意事项
以下是我对MySQL建表时的注意事项。其实,建表事项有很多,我的总结如下: 1 存储引擎的选择,一般做开发,都是要支持事务的,所以选择InnoDB 2 对字段类型的选择: 对于日期类型如果要记录时分…...
Advanced RAG 09:『提示词压缩』技术综述
编者按: 如何最大限度地发挥 LLMs 的强大能力,同时还能控制其推理成本?这是当前业界研究的一个热点课题。 针对这一问题,本期精心选取了一篇关于"提示词压缩"(Prompt Compression)技术的综述文章。正如作者所说…...
DroneCAN 适配器节点(二))
(13)DroneCAN 适配器节点(二)
文章目录 前言 2 固件 2.1 基于F103 2.2 基于F303 2.3 基于F431 3 ArduPilot固件DroneCAN设置 3.1 f303-通用设置示例 4 DroneCAN适配器节点 前言 这些节点允许现有的 ArduPilot 支持的外围设备作为 DroneCAN 或 MSP 设备适应 CAN 总线。这也允许扩展自动驾驶仪硬件的…...
摸鱼大数据——Spark基础——Spark环境安装——Spark Local[*]搭建
一、虚拟机配置 查看每一台的虚拟机的IP地址和网关地址 查看路径: cat /etc/sysconfig/network-scripts/ifcfg-ens33 2.修改 VMware的网络地址: 使用VMnet8 3.修改windows的对应VMware的网卡地址 4.通过finalshell 或者其他的shell连接工具即可连接使用即可, 连接后, 测试一…...
)
函数内部结构分层浅析(从MVC分层架构联想)
函数内部结构分层浅析(从MVC分层架构联想) 分层架构:一种将软件代码按不同功能进行划分的架构模式。 优点包括: 可维护性:各层职责明确,易于单独修改维护。 可扩展性:方便添加或修改某一层,不…...

【three.js案例二】时空隧道
import * as THREE from ./build/three.module.js // 引入轨道控制器扩展库OrbitControls.js import { OrbitControls } from three/addons/controls/OrbitControls.js; // 引入dat.gui.js的一个类GUI import { GUI } from three/addons/libs/lil-gui.module.min.js;// 场景 co…...

动手学深度学习(Pytorch版)代码实践 -计算机视觉-48全连接卷积神经网络(FCN)
48全连接卷积神经网络(FCN) 1.构造函数 import torch import torchvision from torch import nn from torch.nn import functional as F import matplotlib.pyplot as plt import liliPytorch as lp from d2l import torch as d2l# 构造模型 pretrained…...

【Python游戏】猫和老鼠
本文收录于 《一起学Python趣味编程》专栏,从零基础开始,分享一些Python编程知识,欢迎关注,谢谢! 文章目录 一、前言二、代码示例三、知识点梳理四、总结一、前言 本文介绍如何使用Python的海龟画图工具turtle,开发猫和老鼠游戏。 什么是Python? Python是由荷兰人吉多范…...

【无标题】c# WEBAPI 读写表到Redis
//c# WEBAPI 读写表到Redis using System; using System.Collections.Generic; using System.Linq; using System.Net; using System.Net.Http; using System.Web.Http; using Newtonsoft.Json; using StackExchange.Redis; using System.Data; using System.Web; namespace …...
)
【剑指Offer系列】53-0到n中缺失的数字(index)
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。 示例 1: 输入:nums [3,0,1] 输出:2 解释:n 3,因为有 3 个数字,所以所有的数字都在范围 [0,3]…...

docker compose部署zabbix7.0官方方法快速搭建
环境介绍: 系统:centos7 官方文档:https://www.zabbix.com/documentation/current/zh/manual/installation/containers docker镜像加速 vi /etc/docker/daemon.json{"registry-mirrors": ["https://docker.1panel.live&quo…...
?)
分库分表之后如何设计主键ID(分布式ID)?
文章目录 1、数据库的自增序列步长方案2、分表键结合自增序列3、UUID4、雪花算法5、redis的incr方案总结 在进行数据库的分库分表操作后,必然要面临的一个问题就是主键id如何生成,一定是需要一个全局的id来支持,所以分库分表之后,…...
秋招突击——6/28、6.29——复习{数位DP——度的数量}——新作{}
文章目录 引言复习数位DP——度的数量个人实现参考实现 总结 引言 头一次产生了那么强烈的动摇,对于未来没有任何的感觉的,不知道将会往哪里走,不知道怎么办。可能还是因为实习吧,再加上最近复习也没有什么进展,并不知…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
