推荐系统三十六式学习笔记:原理篇.模型融合14|一网打尽协同过滤、矩阵分解和线性模型
目录
- 从特征组合说起
- FM模型
- 1.原理
- 2.模型训练
- 3.预测阶段
- 4.一网打尽其他模型
- 5.FFM
- 总结
在上一篇文章中,我们讲到了使用逻辑回归和梯度提升决策树组合的模型融合办法,用于CTR预估,给这个组合起了个名字,叫“辑度组合”。这对组合中,梯度提升决策树GBDT,所起的作用就是对原始的特征做各种有效的组合,一颗树一个叶子节点就是一种特征组合。
从特征组合说起
从逻辑回归最朴素的特征组合就是二阶笛卡尔乘积,但是这种暴力组合存在如下问题:
1.两两组合导致特征维度灾难;
2.组合后的特征不见得都有效,事实上大部分可能无效;
3.组合后的特征样本非常稀疏,即组合容易,但是样本中可能不存在对应的组合,也就没办法在训练时更新参数。
如果把包含了特征两两组合的逻辑回归线性部分写出来,就是:
y ^ = ω 0 + ∑ i = 1 n ω i x i + ∑ i = 1 n ∑ j = j + 1 n ω i j x i x j \hat{y} = ω_0 +\sum_{i=1}^n{ω_ix_i} +\sum_{i=1}^n\sum_{j=j+1}^n{ω_{ij}x_ix_j} y^=ω0+i=1∑nωixi+i=1∑nj=j+1∑nωijxixj
这和原始的逻辑回归相比,多了后面的部分,特征两两组合,也需要去学习对应的参数权重。
问题是两两组合后可能没有样本能欧学习到$w_{ij},在应用中,对于这些组合,也只能放弃,因为没有学到权重。
针对这个问题,就有了一个新的算法模型:因子分解机模型,也叫FM,即Factorization Machine。因子分解机也常常用来做模型融合。
FM模型
1.原理
因子分解机模型是在2010年被提出,因为逻辑回归在做特征组合时样本稀疏,无法学习到很多特征组合的权重,所以因子分解机的提出者就想,能否对上面那个公式中的 w i j w_{ij} wij做解耦,让每一个特征学习一个隐因子向量出来。
正如矩阵分解时,为每一个用户和每一个物品各自都学习一个隐因子向量,这样,任何两个特征需要组合时,只需隐因子变量做向量点积,就是两者组合特征的权重了。
针对逻辑回归的线性部分:
y ^ = ω 0 + ∑ i = 1 n ω i x i + ∑ i = 1 n ∑ j = i + 1 n < v i , v j > x i x j \hat{y} =\omega_{0} + \sum_{i=1}^n{\omega_{i}x_{i}} + \sum_{i=1}^{n}{\sum_{j=i+1}^{n}}{<v_i,v_j>x_ix_j} y^=ω0+i=1∑nωixi+i=1∑nj=i+1∑n<vi,vj>xixj
这个公式和前面特征组合的公式相比,不同之处就是原来有个\omega_{ij},变成了两个隐因子向量的点积<V_i,V_j>。
它认为两个特征之间,即便没有出现在一条样本中,也是有间接联系的。比如特征A和特征B,出现在一些样本中,特征B和特征C也出现在一些样本中,那么特征A和特征C无论是否出现在一些样本中,我们有理由认为两个特征仍然有些联系。
如果在实际预测CTR时,特征A和特征C真的同时出现在一些样本中,如果你用的是因子分解模型,你可以直接取特征A和特征C的隐因子向量,进行点积计算,就得到两者组合的权重。因子分解机的先进之处就在于此。
既然二阶组合特征可以学到隐因子向量,那么三阶、四阶、五阶呢?实际上,组合越多,计算复杂度就会陡增,一般在实际使用中,因子分解机多用在二阶特征组合中。
2.模型训练
因子分解机的参数学习并无特别之处,看目标函数,这里是把他当做融合模型来看的,用来做CTR预估,因预测目标是一个二分类,因子分解机的输出还需要经过sigmoid函数变换:
σ ( y ^ ) = 1 1 + e − y ^ \sigma(\hat{y}) =\frac{1}{1+ e^{-\hat{y}}} σ(y^)=1+e−y^1
因此损失目标函数为:
l o s s ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( σ ( y ^ ) ) + ( 1 − y ( i ) ) l o g ( 1 − σ ( y ^ ) ] loss(\theta) = - \frac{1}{m}\sum_{i=1}^m{[y^{(i)} log(\sigma(\hat{y})) + (1-y^{(i)})log(1-\sigma(\hat{y}) ]} loss(θ)=−m1i=1∑m[y(i)log(σ(y^))+(1−y(i))log(1−σ(y^)]
公式中 σ ( y ^ ) \sigma(\hat{y}) σ(y^) 是因子分解机的预测输出后经过sigma函数变换得到的预估CTR, y ^ \hat{y} y^是真实样本的类别标记,正样本为1,负样本为0,m是样本总数。
对于这个损失目标函数使用梯度下降或者随机梯度下降,就可以得到模型的参数,注意函数实际上还需要加上正则项。
3.预测阶段
因子分解机中二阶特征组合那一部分,在实际计算时,复杂度有点高,如果隐因子向量的维度是k,特征维度是n,那么这个复杂度为O(kn^2),其中n方是特征要两两组合,k是每次组合都要对k维向量计算
点积。需稍微改造一下,改造过程如下:
loop1 begin: 循环k次,k就是隐因子向量的维度,其中,循环到第f次时做以下事情loop2 begin:循环n个特征,第i次循环时做这样的事情1. 从第i个特征的隐因子向量中拿出第f维的值2. 计算两个值:A是特征值和f维的值相乘,B是A的平方loop2 end把n个A累加起来,并平方得到C,把n个B也累加起来,得到D用C减D,得到Eloop1 end把k次循环得到的k个E累加起来,除以2这就是因子分解机中,二阶组合部分的实际计算方法,目前复杂度下降为O(kn)。
4.一网打尽其他模型
下面继续带你见识一些因子分解机的神奇之处。看下面这张图:

下面继续带你见识一些因子分解机的神奇之处。看下面这张图:
这张图中的每一条样本都记录了用户对电影的评分,最右边的y是评分,也就是预测目标;左边的特征有五种,用户ID、当前评分的电影ID、曾经评过的其他分、评分时间、上一次评分的电影。
现在我们来看因子分解机如何一网打尽其他模型的,这里说的打败是说模型可以变形成其他模型。
前面例子,因子分解机实现了带有特征组合的逻辑回归。
现在假设图中的样本特征只留下用户ID和电影ID,因子分解机模型就变成:
y ^ = ω 0 + ω u + ω i + < V u , V i > \hat{y} =\omega_{0} + \omega_{u} + \omega_{i} + <V_{u},V_{i}> y^=ω0+ωu+ωi+<Vu,Vi>
用户ID和电影ID,在一条样本中,各自都只有一个维度1,其他都是0。所以在一阶部分就没有了求和符号,直接是 w u w_u wu和 w i w_i wi,二阶部分乘积也只剩下了1,其他都为0,就转变为偏置信息的SVD。
继续,在SVD基础上把样本中的特征加上用户历史评分过的电影ID,再求隐因子向量,就转变为SVD++;再加上时间信息,就变成了time-SVD。
因子分解机把前面讲过的矩阵分解一网打尽了,顺便还干起了逻辑回归的工作。正因为如此,因子分解机常常用来做模型融合,在推荐系统的排序阶段肩负起对召回结果做重排序的任务。
5.FFM
在因子分解机基础上可以进行改进,改进思路是:不但认为特征和特征之间潜藏着一些关系,还认为特征和特征类型也有千丝万缕的关系。
这个特征类型,就是某些特征实际上来自数据的同一个字段。比如用户id,占据了很多维度,变成了很多特征,但他们都属于同一个类型,都叫做用户ID。这个特征类型就是字段,即Field.所以这种改进叫做Field-aware Factorization Machines ,简称FFM。
因子分解机模型如下:
y ^ = ω 0 + ∑ i = 1 n ω i x i + ∑ i = 1 n ∑ j = i + 1 n < V i , V j > x i x j \hat{y} =\omega_{0} + \sum_{i=1}^n{\omega_{i} x_{i}} + \sum_{i=1}^n{\sum_{j=i+1}^{n}{<V_i,V_j>x_ix_j}} y^=ω0+i=1∑nωixi+i=1∑nj=i+1∑n<Vi,Vj>xixj
之前因子分解机认为每个特征有一个隐因子向量,FFM改进的是二阶组合那部分,改进的模型认为每个特征有f个隐因子向量,这里的f就是特征一共来自都少个字段(Field),二阶组合部分改进后如下:
∑ j = 1 n ∑ j = i + 1 n < V i , f j , V j , f i > x i x j \sum_{j=1}^n{\sum_{j=i+1}^n{<V_{i,fj},V_{j,fi}>x_ix_j}} j=1∑nj=i+1∑n<Vi,fj,Vj,fi>xixj
FFM模型也常用来做CTR预估,在FM和FFM事件过程中,记得要对样本和特征做归一化。
总结
今天,我给你介绍了另一种常用来做CTR预估的模型,因子分解机。因子分解机最早提出在2010年,在一些数据挖掘比赛中取得了不错的成绩,后来被引入到工业界做模型融合,也表现不俗。
严格来说,因子分解机也算是矩阵分解算法的一种,因为它的学习结果也是隐因子向量,也是用隐因子向量的乘积来代替单个权重参数。
相关文章:

推荐系统三十六式学习笔记:原理篇.模型融合14|一网打尽协同过滤、矩阵分解和线性模型
目录 从特征组合说起FM模型1.原理2.模型训练3.预测阶段4.一网打尽其他模型5.FFM 总结 在上一篇文章中,我们讲到了使用逻辑回归和梯度提升决策树组合的模型融合办法,用于CTR预估,给这个组合起了个名字,叫“辑度组合”。这对组合中&…...
如何使用mapXplore将SQLMap数据转储到关系型数据库中
关于mapXplore mapXplore是一款功能强大的SQLMap数据转储与管理工具,该工具基于模块化的理念开发,可以帮助广大研究人员将SQLMap数据提取出来,并转储到类似PostgreSQL或SQLite等关系型数据库中。 功能介绍 当前版本的mapXplore支持下列功能…...
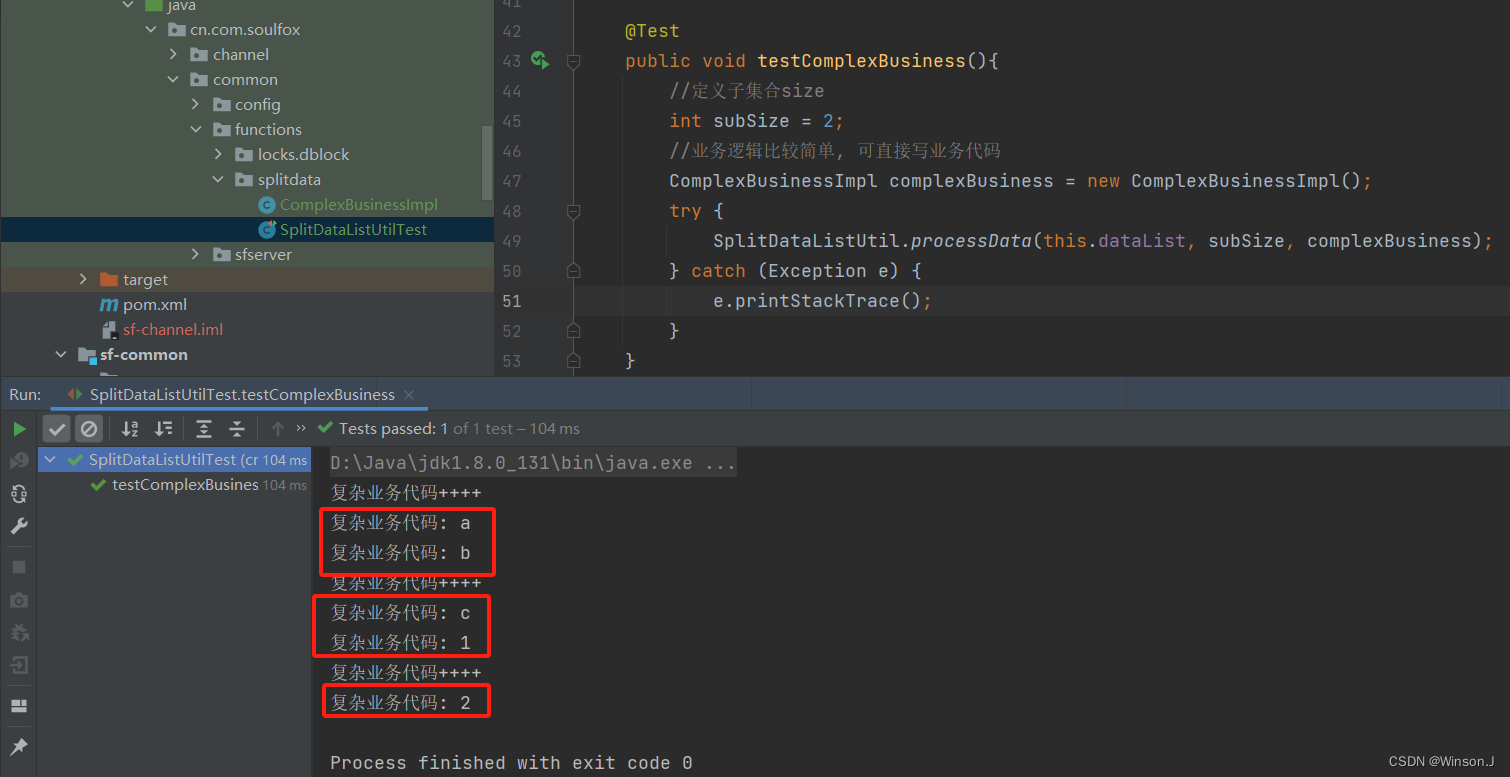
JAVA设计模式-大集合数据拆分
背景 我们在做软件开发时,经常会遇到把大集合的数据,拆分成子集合处理。例如批量数据插入数据库时,一次大约插入5000条数据比较合理,但是有时候待插入的数据远远大于5000条。这时候就需要进行数据拆分。数据拆分基本逻辑并不复杂&…...

如何使用sr2t将你的安全扫描报告转换为表格格式
关于sr2t sr2t是一款针对安全扫描报告的格式转换工具,全称为“Scanning reports to tabular”,该工具可以获取扫描工具的输出文件,并将文件数据转换为表格格式,例如CSV、XLSX或文本表格等,能够为广大研究人员提供一个…...

ansible自动化运维,(2)ansible-playbook
三种常见的数据格式: XML:可扩展标记语言,用于数据交换和配置 JSON:对象标记法,主要用来数据交换或配置,不支持注释 YAML:不是一种标记语言,主要用来配置,大小写敏感&…...

一分钟学习数据安全—自主管理身份SSI分布式标识DID介绍
SSI标准化的两大支柱,一个是VC,之前简单介绍过,另一个就是DID。基本层次上,DID就是一种新型的全局唯一标识符,跟浏览器的URL没有什么不同。深层次上,DID是互联网分布式数字身份和PKI新层级的原子构件。 一…...

[单master节点k8s部署]11.服务service
service service是一个固定接入层,客户端 可以访问service的ip和端口,访问到service关联的后端pod,这个service工作依赖于dns服务(coredns) 每一个k8s节点上都有一个组件叫做kube-proxy,始终监视着apiser…...

ES6面试题——箭头函数和普通函数有什么区别
1. this指向问题 <script> let obj {a: function () {console.log(this); // 打印出:{a: ƒ, b: ƒ}},b: () > {console.log(this); // 打印出Window {window: Window, self: Window,...}}, }; obj.a(); obj.b(); </script> 箭头函数中的this是在箭…...
WordPress中文网址导航栏主题风格模版HaoWa
模板介绍 WordPress响应式网站中文网址导航栏主题风格模版HaoWa1.3.1源码 HaoWA主题风格除行为主体导航栏目录外,对主题风格需要的小控制模块都开展了敞开式的HTML在线编辑器方式的作用配备,另外预埋出默认设置的编码构造,便捷大伙儿在目前…...

ThreadPoolExecutor基于ctl变量的声明周期管理
个人博客 ThreadPoolExecutor基于ctl变量的声明周期管理 | iwts’s blog 总集 想要完整了解下ThreadPoolExecutor?可以参考: 基于源码详解ThreadPoolExecutor实现原理 | iwts’s blog ctl字段的应用 线程池内部使用一个变量ctl维护两个值ÿ…...

运维锅总详解Prometheus
本文尝试从Prometheus简介、架构、各重要组件详解、relable_configs最佳实践、性能能优化及常见高可用解决方案等方面对Prometheus进行详细阐述。希望对您有所帮助! 一、Prometheus简介 Prometheus 是一个开源的系统监控和报警工具,最初由 SoundCloud …...
)
深入解析Tomcat:Java Web服务器(上)
深入解析Tomcat:Java Web服务器(上) Apache Tomcat是一个开源的Java Web服务器和Servlet容器,用于运行Java Servlets和JavaServer Pages (JSP)。Tomcat在Java Web应用开发中扮演着重要角色。本文将详细介绍Tomcat的基本概念、安装…...

【第9章】MyBatis-Plus持久层接口之SimpleQuery
文章目录 前言一、使用步骤1.引入 SimpleQuery 工具类2.使用 SimpleQuery 进行查询 二、使用提示三、功能详解1. keyMap1.1 方法签名1.2 参数说明1.3 使用示例1.4 使用提示 2. map2.1 方法签名2.2 参数说明2.3 使用示例2.4 使用提示 3. group3.1 方法签名3.2 参数说明3.3 使用示…...
一文带你了解乐观锁和悲观锁的本质区别!
文章目录 悲观锁是什么?乐观锁是什么?如何实现乐观锁?什么是CAS应用局限性ABA问题是什么? 悲观锁是什么? 悲观锁它总是假设最坏的情况,它会认为共享资源在每次被访问的时候就会出现线程安全问题࿰…...
Android Studio环境搭建(4.03)和报错解决记录
1.本地SDK包导入 安装好IDE以及下好SDK包后,先不要管IDE的引导配置,直接新建一个新工程,进到开发界面。 SDK路径配置:File---->>Other Settings---->>Default Project Structure 拷贝你SDK解压的路径来这,…...

基于协同过滤的电影推荐与大数据分析的可视化系统
基于协同过滤的电影推荐与大数据分析的可视化系统 在大数据时代,数据分析和可视化是从大量数据中提取有价值信息的关键步骤。本文将介绍如何使用Python进行数据爬取,Hive进行数据分析,ECharts进行数据可视化,以及基于协同过滤算法…...
修复vcruntime140.dll方法分享
修复vcruntime140.dll方法分享 最近在破解typora的时候出现了缺失vcruntime140.dll文件的报错导致软件启动失败。所以找了一番资料发现都不是很方便的处理,甚至有的dll处理工具还需要花钱????,我本来就是为…...

PostgreSQL的系统视图pg_stat_wal_receiver
PostgreSQL的系统视图pg_stat_wal_receiver 在 PostgreSQL 中,pg_stat_wal_receiver 视图提供了关于 WAL(Write-Ahead Logging)接收进程的统计信息。WAL 接收器是 PostgreSQL 集群中流复制的一部分,它在从节点中工作,…...
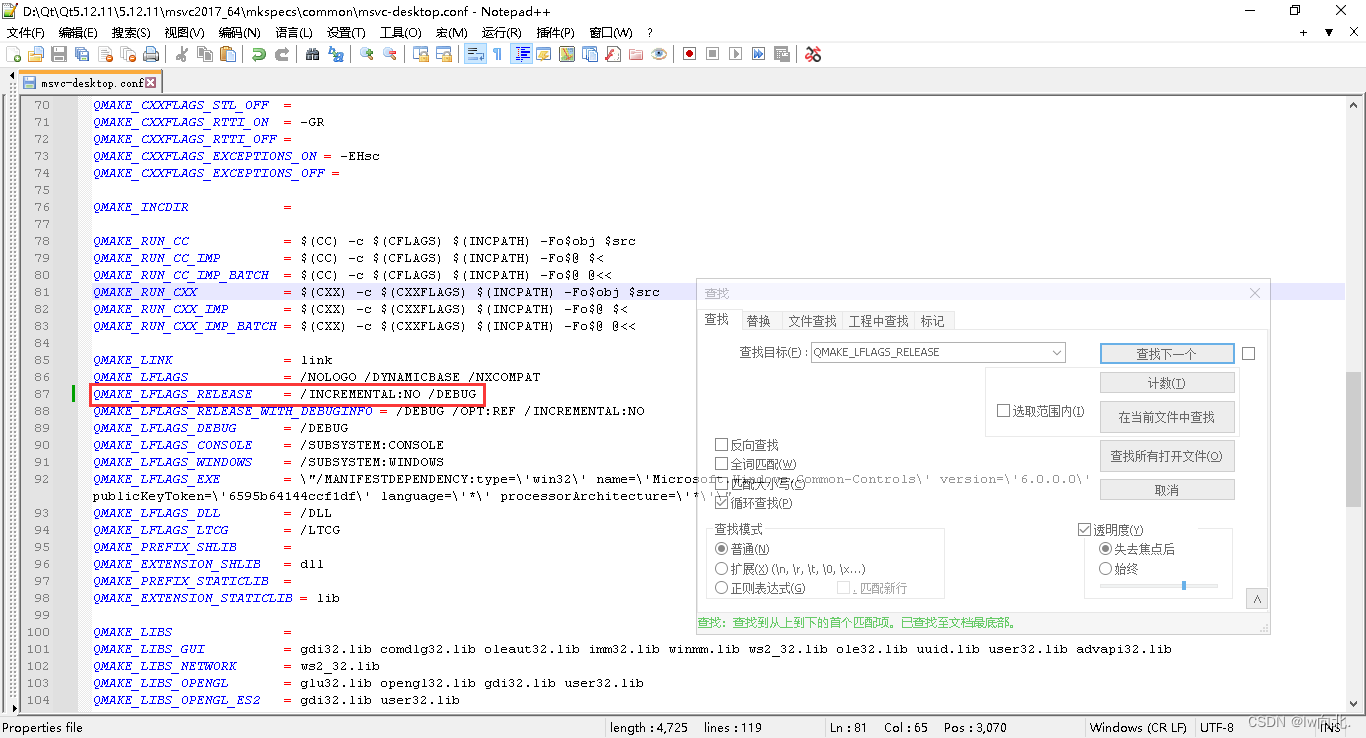
Qt之Pdb生成及Dump崩溃文件生成与调试(含注释和源码)
文章目录 一、Pdb生成及Dump文件使用示例图1.Pdb文件生成2.Dump文件调试3.参数不全Pdb生成的Dump文件调试 二、个人理解1.生成Pdb文件的方式2.Dump文件不生产的情况 三、源码Pro文件mian.cppMainWindowUi文件 总结 一、Pdb生成及Dump文件使用示例图 1.Pdb文件生成 下图先通过…...

视频号视频怎么保存到手机,视频号视频怎么保存到手机相册里,苹果手机电脑都可以用
随着数字媒体的蓬勃发展,视频已成为我们日常生活中不可或缺的一部分。视频号作为众多视频分享平台中的一员,吸引了大量用户上传和分享各类精彩视频。然而,有时我们可能希望将视频号上的视频下载下来,以下将详细介绍如何将视频号的视频。 方法…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
