力扣每日一题 6/30 记忆化搜索/动态规划
- 博客主页:誓则盟约
- 系列专栏:IT竞赛 专栏
- 关注博主,后期持续更新系列文章
- 如果有错误感谢请大家批评指出,及时修改
- 感谢大家点赞👍收藏⭐评论✍



494.目标和【中等】
题目:
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
分析问题:
设 nums 的元素和为 s,添加正号的元素之和为 p,添加负号的元素(绝对值)之和为 q,那么有
- p+q=s
- p-q=target
化简得:
- p = (s+target) / 2
- q = (s-target) / 2
我们找所有元素里面选取出来的元素和恰好为p的方案个数,那么这就变成了一道经典的0-1背包问题的变形,找恰好装capacity,求方案数/最大/最小价值和,capacity指的是容量,也就是这里的负数的和的绝对值。
那么我们就可以根据传统的0-1背包问题的求解过程来解题,带上cache数组以便达到记忆化的一个效果。

此处也可以进行进一步的优化,用一个二维数组f来替代递推函数dfs:
首先创建一个二维数组f,其中n表示数组的长度,target表示目标值,该数组用于记录不同状态下的结果。
然后将f[0][0]初始化为1,这是一个基础的起始条件。接下来通过两个嵌套循环进行计算。外层循环遍历一个名为nums的数组,其中的每个元素x代表物品的价值。内层循环遍历目标值target的所有可能取值。在循环内部,根据不同条件更新f数组的值。
- 如果c小于x,说明当前考虑的物品价值x大于当前的目标值c,无法选择该物品,所以f[i + 1][c]保持与f[i][c]相同。
- 如果c大于或等于x,那么f[i + 1][c]等于f[i][c]加上f[i][c - x],这表示在这种情况下,可以选择该物品,所以要将不选择该物品的情况(f[i][c])和选择该物品的情况(f[i][c - x])的结果相加。
最后,函数返回f[n][target],即最终在考虑了所有物品和目标值的情况下的结果。
代码实现:
优化前:
class Solution:def findTargetSumWays(self, nums: list[int], target: int) -> int:# p = (s+t) /2target += sum(nums)if target < 0 or target % 2:return 0target //=2n=len(nums)@cache # 保存记忆def dfs(i,c): # i是剩余多少个物品没装 c是当前背包剩余容量if i<0:return 1 if c==0 else 0if c < nums[i]:return dfs(i-1,c)return dfs(i-1,c)+dfs(i-1,c-nums[i])return dfs(n-1,target)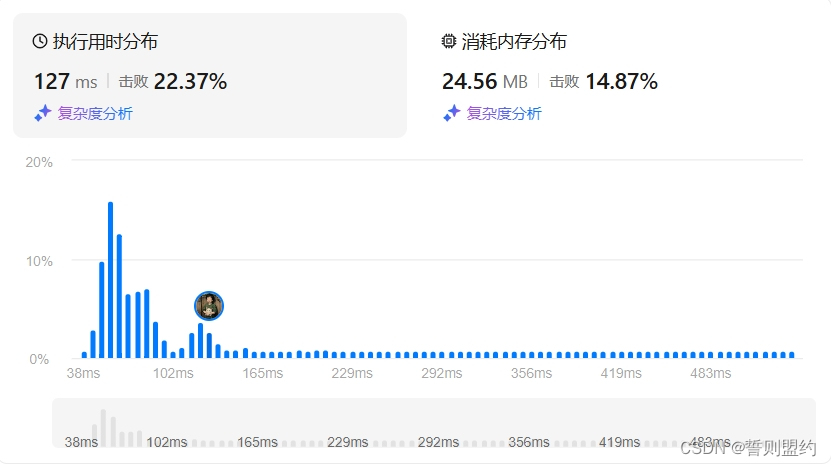
优化后:
class Solution:def findTargetSumWays(self, nums: list[int], target: int) -> int:# p = (s+t) /2target += sum(nums)if target < 0 or target % 2:return 0target //=2n=len(nums)f=[[0]*(target+1) for _ in range(n+1)]f[0][0]=1for i,x in enumerate(nums):for c in range(target+1):if c<x: f[i+1][c] = f[i][c]else: f[i+1][c] = f[i][c] + f[i][c-x]return f[n][target]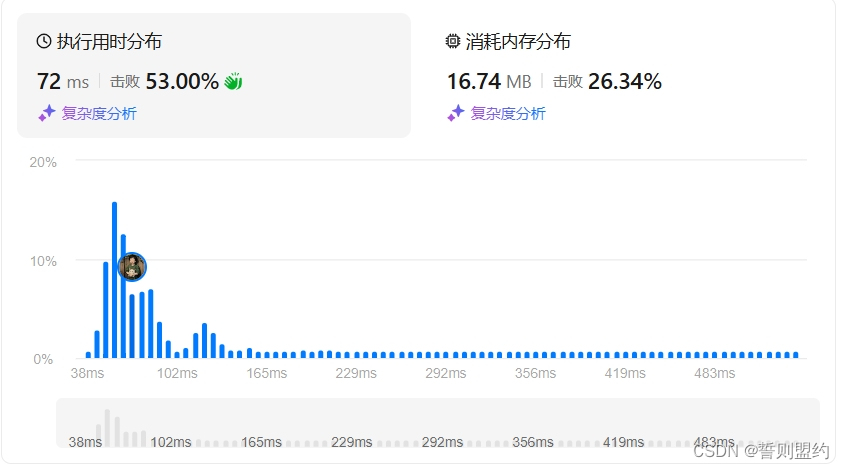
总结:
优化后代码详细解释:
target += sum(nums):将target值加上数组nums的元素总和,得到p的2倍。if target < 0 or target % 2::检查新的target值是否小于0或是否为奇数。如果是,则直接返回0,表示无法得到目标值。target //= 2:将target值除以2,得到用于后续计算的新值。n = len(nums):获取数组nums的长度。f = [[0] * (target + 1) for _ in range(n + 1)]:创建一个二维数组f,用于动态规划的计算。f[0][0] = 1:设置初始状态,即当没有元素且目标值为0时,有一种方法可以达到。- 通过两个嵌套循环进行动态规划计算:
- 外层循环
for i, x in enumerate(nums):遍历数组nums的每个元素。 - 内层循环
for c in range(target + 1):遍历所有可能的目标值。 - 在循环内部,根据当前元素
x和目标值c的关系更新f[i + 1][c]的值。如果c < x,则f[i + 1][c] = f[i][c],表示无法选择当前元素来达到目标值;如果c >= x,则f[i + 1][c] = f[i][c] + f[i][c - x],表示可以选择或不选择当前元素来达到目标值,将两种情况的方法数相加。
- 外层循环
- 最后,函数返回
f[n][target],即使用整个数组nums达到最终目标值的方法数。
考点:
- 动态规划的应用:通过构建二维数组来记录不同状态下的结果,根据状态转移方程进行计算。
- 对问题的数学转化:将原问题转化为通过加减运算得到特定值的问题,并进行了一些预处理和条件判断。
收获:
- 深入理解了动态规划的思想和应用方法,学会如何根据问题的特点构建合适的状态和状态转移方程。
- 提高了对问题进行数学分析和转化的能力,能够将复杂的问题简化为可计算的形式。
- 增强了对数组操作和循环的熟练程度,能够灵活运用这些基本编程技巧来解决实际问题。

“对于我们的幸福来说,别人的看法在本质上来讲并不十分重要。”——《人生的智慧》
相关文章:

力扣每日一题 6/30 记忆化搜索/动态规划
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 494.目标和【中等】 题目: 给你一个非负整数数组 nums 和一个…...

图像基础知识入门【图像概念不同图像格式】
图像基础知识入门【图像概念&不同图像格式】 最近有在处理图像转换,因此稍微补足了一下图像相关知识,特在此记录。下面汇总是我根据自己理解和网上查阅资料而来。如有错误,欢迎大家指正。 1 基础概念 像素/分辨率 像素(Pixel)ÿ…...

HP服务器基于SNMP-ilo4的硬件监控指标解读
监控易是一款功能全面的IT基础设施监控软件,它通过SNMP协议与HP服务器内置的ilo4远程管理卡进行通信,实现对HP服务器硬件状态的实时监控。本文将针对监控易中基于SNMP-ilo4的HP服务器硬件监控指标进行解读,帮助运维团队更好地理解和应用这些监…...

Android13系统导航栏添加音量加减键按钮功能
不知道为什么拿到芯片原厂发布给我们的Android13系统源码编译后,导航栏没有音量加减键,客户有反馈这个问题,所以特意加了一下,修改记录如下:frameworks/base目录下 commit 9cb2244d61a237cab03c540bfcca6e4fac2bea2c …...

普及GIS知识,推动产业发展
915 GIS节:普及GIS知识,推动产业发展 自2008年起,每年的9月15日被定为“GIS节”,这一特殊的节日由超图首次发起倡议,旨在打造一个普及和传播GIS(地理信息系统)知识的平台,促进大众对…...
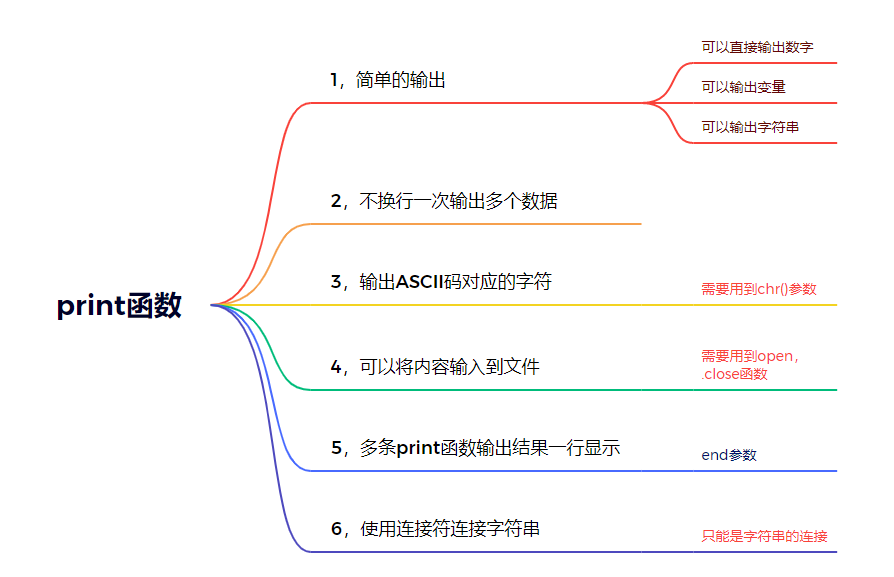
第2章-Python编程基础
#本章目标 1,了解什么是计算机程序 2,了解什么是编程语言 3,了解编程语言的分类 4,了解静态语言与脚本语言的区别 5,掌握IPO程序编写方法 6,熟练应用输出函数print与输入函数input 7,掌握Python…...
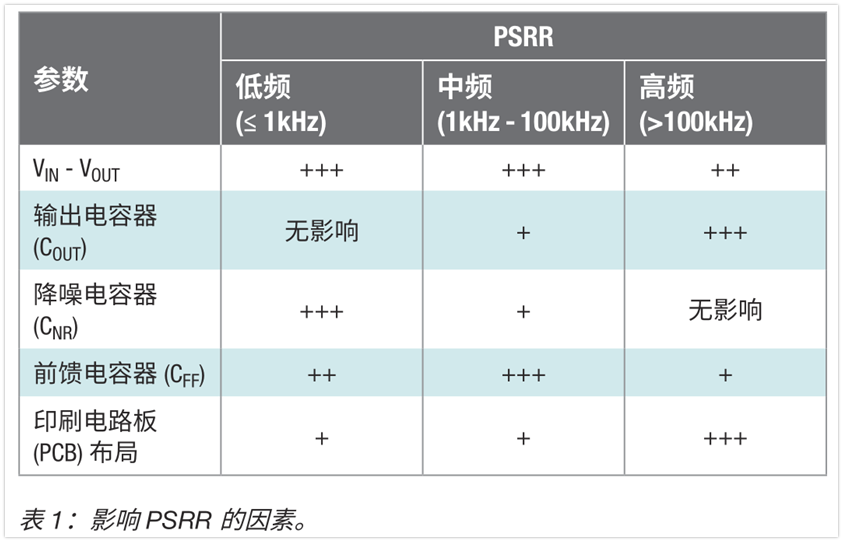
LDO产品的基础知识解析
低压降稳压器 (LDO)是一种用于调节较高电压输入产生的输出电压的简单方法。在大多数情况下,低压降稳压器都易于设计和使用。然而,如今的现代应用都包括各种各样的模拟和数字系统,而有些系统和工作条件将决定哪种LDO最适合相关电路,…...
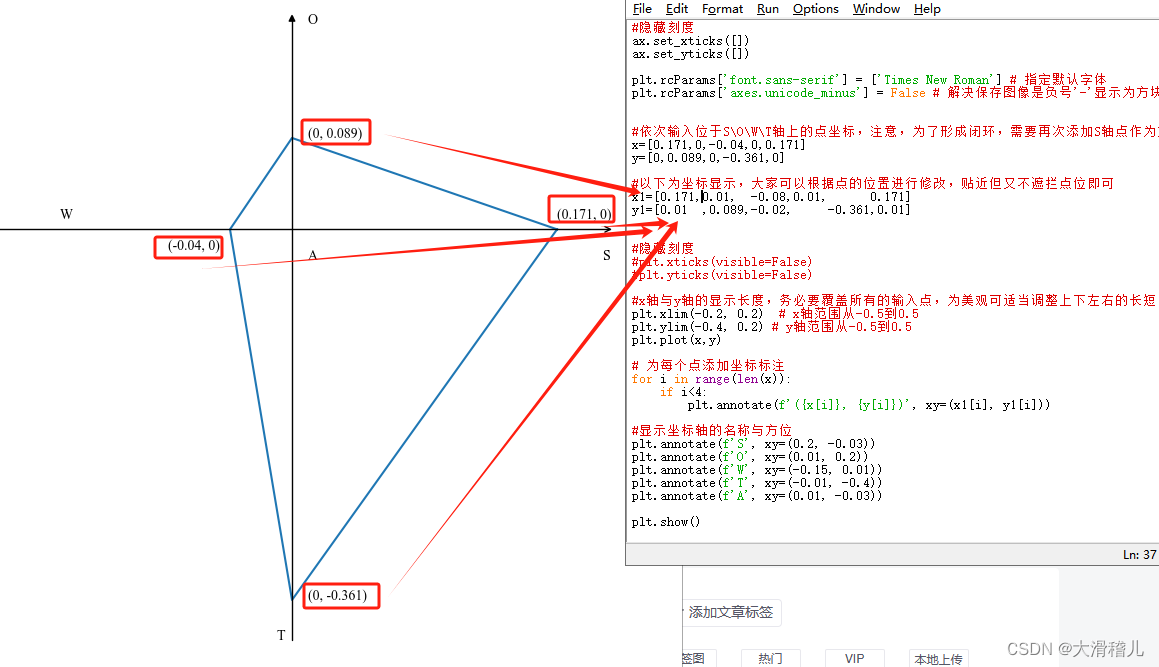
如何利用python画出AHP-SWOT的战略四边形(四象限图)
在企业或产业发展的相关论文分析中,常用到AHP-SWOT法进行定量分析,形成判断矩阵后,如何构造整洁的战略四边形是分析的最后一个环节,本文现将相关代码发布如下: import mpl_toolkits.axisartist as axisartist import …...

适用于智慧城市、智慧文旅等在线场景的轻量级3D数字人引擎MyAvatar简介
本人研发的国内首个纯面向web应用和小程序的轻量级3D虚拟人引擎MyAvatar。 功能简述 支持3D模型定制(写实或卡通风格均可,人物模型需实现绑定和变形)动画可以内置于模型中,也可以单独以glb或fbx格式导出并动态加载支持readyplay…...
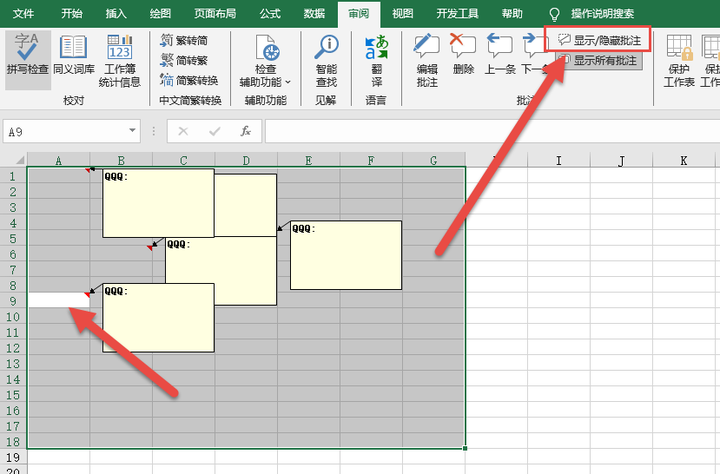
Excel显示/隐藏批注按钮为什么是灰色?
在excel中,经常使用批注来加强数据信息的提示,有时候会把很多的批注显示出来,但是再想将它们隐藏起来,全选工作表后,“显示/隐藏批注”按钮是灰色的,不可用。 二、可操作方法 批注在excel、WPS表格中都是按…...

ArtTS系统能力-通知的学习(3.1)
上篇回顾: ArtTS语言基础类库-容器类库内容的学习(2.10.2) 本篇内容: ArtTS系统能力-通知的学习(3.1) 一、 知识储备 1. 基础类型通知 按内容分成四类: 类型描述NOTIFICATION_CONTENT_BASIC_TEXT普通文…...
—— public_road_planner)
Apollo9.0 PNC源码学习之Planning模块(三)—— public_road_planner
前面文章: (1)Apollo9.0 PNC源码学习之Planning模块(一)—— 规划概览 (2)Apollo9.0 PNC源码学习之Planning模块(二)—— planning_component 1 planning_interface_base 规划接口基类: planning\planning_interface_base\planner_base\planner.h #pragma once#in…...

【Elasticsearch】linux使用supervisor常驻Elasticsearch,centos6.10安装 supervisor
背景: linux服务器,CentOS 6操作系统,默认版本python2.6.6,避免安装过多的依赖不升级python 在网上查的资料python2.6.6兼容supervisor版本 3.1.3 安装supervisor 手动在python官网下载supervisor,并上传到服务器 下…...

推荐系统三十六式学习笔记:原理篇.模型融合14|一网打尽协同过滤、矩阵分解和线性模型
目录 从特征组合说起FM模型1.原理2.模型训练3.预测阶段4.一网打尽其他模型5.FFM 总结 在上一篇文章中,我们讲到了使用逻辑回归和梯度提升决策树组合的模型融合办法,用于CTR预估,给这个组合起了个名字,叫“辑度组合”。这对组合中&…...
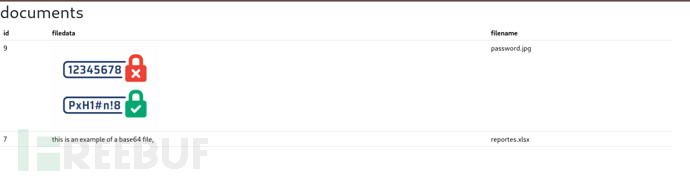
如何使用mapXplore将SQLMap数据转储到关系型数据库中
关于mapXplore mapXplore是一款功能强大的SQLMap数据转储与管理工具,该工具基于模块化的理念开发,可以帮助广大研究人员将SQLMap数据提取出来,并转储到类似PostgreSQL或SQLite等关系型数据库中。 功能介绍 当前版本的mapXplore支持下列功能…...
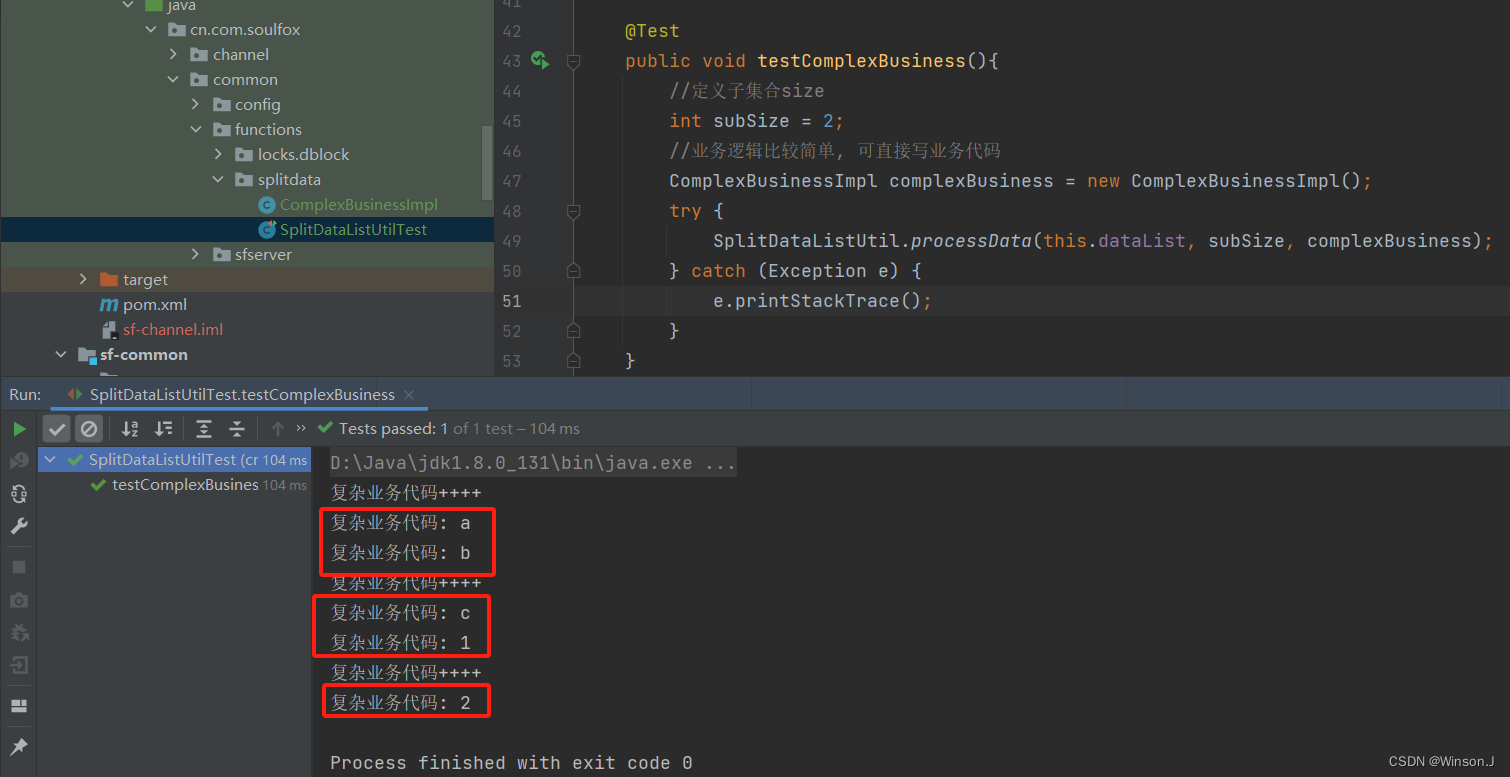
JAVA设计模式-大集合数据拆分
背景 我们在做软件开发时,经常会遇到把大集合的数据,拆分成子集合处理。例如批量数据插入数据库时,一次大约插入5000条数据比较合理,但是有时候待插入的数据远远大于5000条。这时候就需要进行数据拆分。数据拆分基本逻辑并不复杂&…...

如何使用sr2t将你的安全扫描报告转换为表格格式
关于sr2t sr2t是一款针对安全扫描报告的格式转换工具,全称为“Scanning reports to tabular”,该工具可以获取扫描工具的输出文件,并将文件数据转换为表格格式,例如CSV、XLSX或文本表格等,能够为广大研究人员提供一个…...

ansible自动化运维,(2)ansible-playbook
三种常见的数据格式: XML:可扩展标记语言,用于数据交换和配置 JSON:对象标记法,主要用来数据交换或配置,不支持注释 YAML:不是一种标记语言,主要用来配置,大小写敏感&…...

一分钟学习数据安全—自主管理身份SSI分布式标识DID介绍
SSI标准化的两大支柱,一个是VC,之前简单介绍过,另一个就是DID。基本层次上,DID就是一种新型的全局唯一标识符,跟浏览器的URL没有什么不同。深层次上,DID是互联网分布式数字身份和PKI新层级的原子构件。 一…...

[单master节点k8s部署]11.服务service
service service是一个固定接入层,客户端 可以访问service的ip和端口,访问到service关联的后端pod,这个service工作依赖于dns服务(coredns) 每一个k8s节点上都有一个组件叫做kube-proxy,始终监视着apiser…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
