决策树划分属性依据
划分依据
- 基尼系数
- 基尼系数的应用
- 信息熵
- 信息增益
- 信息增益的使用
- 信息增益准则的局限性
最近在学习项目的时候经常用到随机森林,所以对决策树进行探索学习。
基尼系数
基尼系数用来判断不确定性或不纯度,数值范围在0~0.5之间,数值越低,数据集越纯。
基尼系数的计算:
假设数据集有K个类别,类别K在数据集中出现的概率为Pk,则基尼系数为:
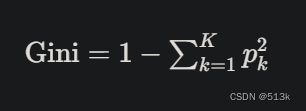
上式是用来求某个节点的基尼系数,要求某个属性的基尼系数用下面的公式:
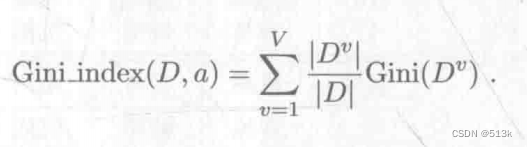
最后选择基尼系数最小的属性进行划分即可。
基尼系数的应用
在决策树中,假如某个节点的基尼系数就是0,此时被分类到这个节点的数据集是纯的,意思就是按照此叶节点的父节点的分类方法来说,此叶节点都是同一个类别的,不需要再次分裂决策。
信息熵
信息熵和基尼系数作用相同,都是用来度量样本集合纯度的指标。
计算方法:
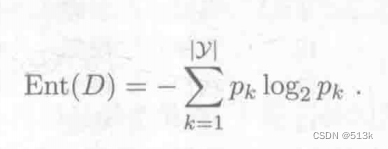
Pk是当前样本集合中第k类样本所占比例,Ent(D)(信息熵)越小,集合D的纯度越高。
这里约定当Pk为0时Ent(D)=0;
信息增益
计算公式: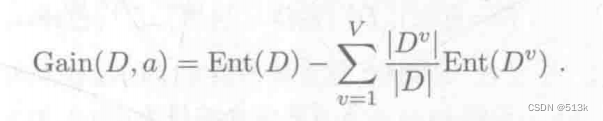
假设现在对集合D使用属性a来进行划分,属性a有v个取值,也就是有v个节点,上式中Dv是第v个节点就是取值为v的样本个数。
信息增益的使用
信息增益越大,说明使用属性a来划分所获得的纯度提升越大,决策树越好。
信息增益准则的局限性
从上面的公式可以看出,信息增益偏好可取值数目较多的属性,假如某个属性可取值达到了n,也就是每个样本都不一样,比如“编号”属性,那可以计算出这个属性的信息增益接近1,选择这样的属性来划分很可能不具有泛化能力。
改进:
使用增益率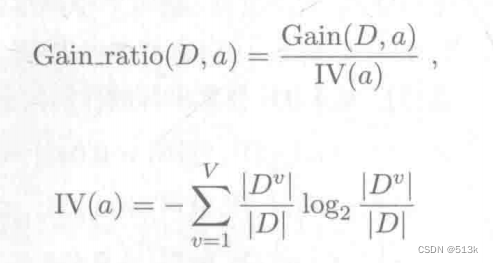
对于这个公式,当属性a的可取值越多时,则IV(a)会越大,增益率变小,进行了平衡。同样的,增益率准则也有局限,它对可取值较少的属性又有所偏好。
最终:先找出信息增益高于平均水平的属性,再从中选择增益率最高的即可。
相关文章:
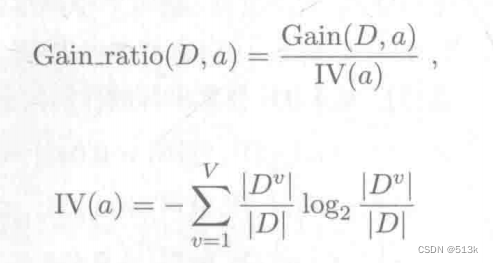
决策树划分属性依据
划分依据 基尼系数基尼系数的应用信息熵信息增益信息增益的使用信息增益准则的局限性 最近在学习项目的时候经常用到随机森林,所以对决策树进行探索学习。 基尼系数 基尼系数用来判断不确定性或不纯度,数值范围在0~0.5之间,数值越低&#x…...
短视频利器 ffmpeg (2)
ffmpeg 官网这样写到 Converting video and audio has never been so easy. 如何轻松简单的使用: 1、下载 官网:http://www.ffmpeg.org 安装参考文档: https://blog.csdn.net/qq_36765018/article/details/139067654 2、安装 # 启用RPM …...
【计算机毕业设计】基于Springboot的智能物流管理系统【源码+lw+部署文档】
包含论文源码的压缩包较大,请私信或者加我的绿色小软件获取 免责声明:资料部分来源于合法的互联网渠道收集和整理,部分自己学习积累成果,供大家学习参考与交流。收取的费用仅用于收集和整理资料耗费时间的酬劳。 本人尊重原创作者…...

【2024】LeetCode HOT 100——图论
目录 1. 岛屿数量1.1 C++实现1.2 Python实现1.3 时空分析2. 腐烂的橘子2.1 C++实现2.2 Python实现2.3 时空分析3. 课程表3.1 C++实现3.2 Python实现3.3 时空分析4. 实现 Trie (前缀树)4.1 C++实现4.2 Python实现4.3 时空分析1. 岛屿数量 🔗 原题链接:200. 岛屿数量 经典的Fl…...

解析Java中1000个常用类:Currency类,你学会了吗?
在线工具站 推荐一个程序员在线工具站:程序员常用工具(http://cxytools.com),有时间戳、JSON格式化、文本对比、HASH生成、UUID生成等常用工具,效率加倍嘎嘎好用。程序员资料站 推荐一个程序员编程资料站:程序员的成长之路(http://cxyroad.com),收录了一些列的技术教程…...

5.x86游戏实战-CE定位基地址
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 本次游戏没法给 内容参考于:微尘网络安全 上一个内容:4.x86游戏实战-人物状态标志位 上一个内容通过CE未知的初始值、未变动的数值、…...

istitle()方法——判断首字母是否大写其他字母小写
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 语法参考 istitle()方法用于判断字符串中所有的单词首字母是否为大写而其他字母为小写。istitle()方法的语法格式如下: str.istitle() …...

Linux实用命令练习
目录 一、常用命令 二、系统命令 三、用户和组 四、权限 五、文件相关命令 六、查找 七、正则表达式 八、输入输出重定向 九、进程控制 十、其他命令 1、远程文件复制:scp 2、locate查找 3、which命令 4、设置或显示环境变量:export 5、修…...

刷题——二叉搜索树与双向链表
二叉搜索树与双向链表_牛客题霸_牛客网 方法一: void dfs(TreeNode* pRootOfTree, TreeNode* &pre){if(pRootOfTree NULL)return;dfs(pRootOfTree->left, pre);//所有左子树if(pre)pre->right pRootOfTree;pRootOfTree->left pre;pre pRootOfTree…...
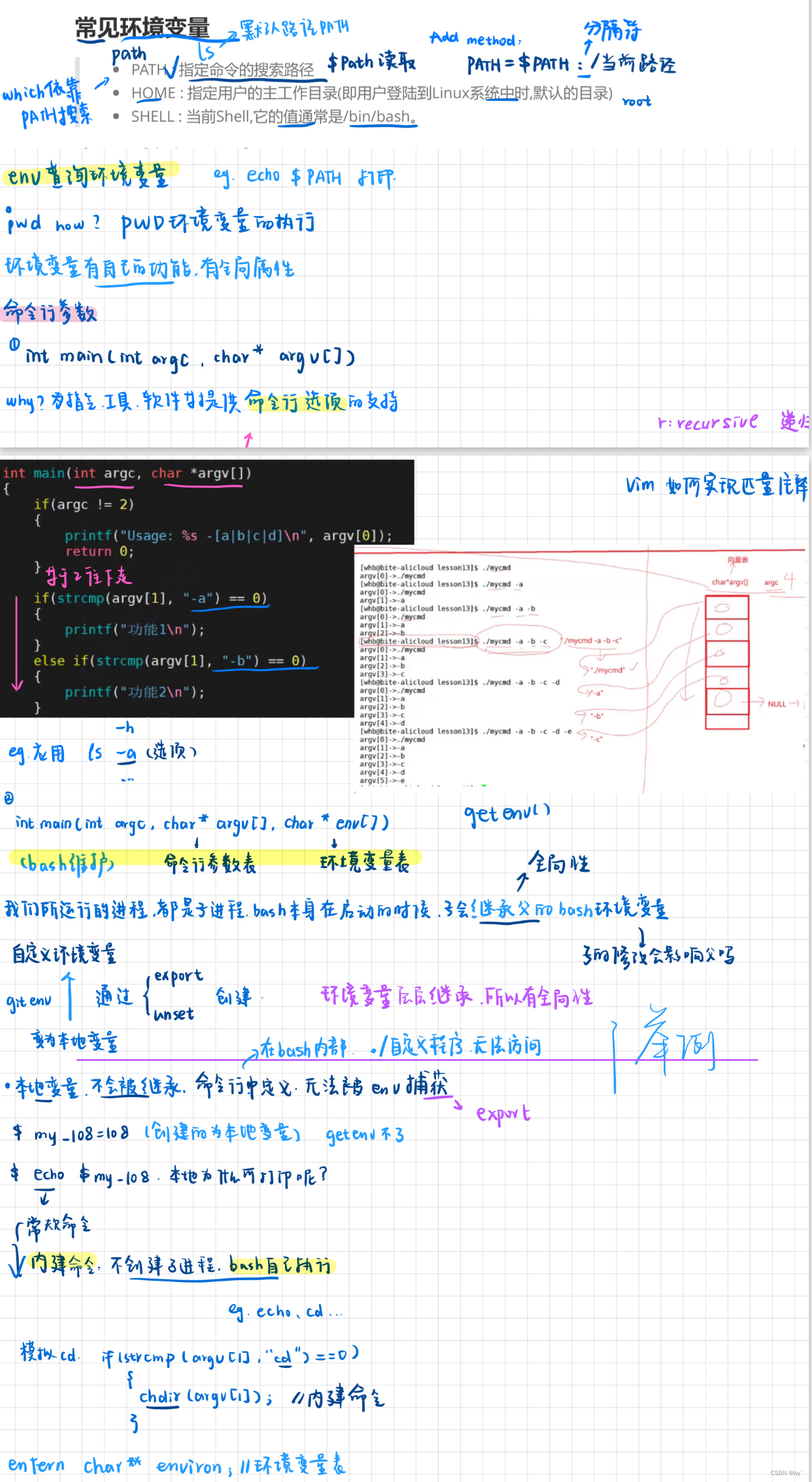
【Linux】进程优先级 | 环境变量
目录 Ⅰ. 进程优先级(Process Priority) 1. 什么是进程优先级? 2. 查看系统进程 3. 修改进程优先级 4.优先级调度原理 Ⅱ. 进程的切换(Process Switch) 1. 竞争与独立 2. 并行与并发 3. 进程抢占 4.实现切换…...

最新手动迁移WordPress方法
手动迁移WordPress网站主要步骤有:迁移文件、迁移数据库、修复数据库连接。 对于WordPress Installations,只有两个主要组件,您需要访问手动将安装迁移到新主机:文件和数据库。 迁移文件 将文件从旧主机迁移到新的最简单方法之…...
ChatGPT在程序开发中的应用:提升生产力的秘密武器
在当今飞速发展的科技时代,程序开发已经成为许多企业和个人必不可少的技能。然而,编写代码并非总是顺风顺水,面对复杂的算法、繁琐的调试、持续不断的需求变更,程序员们常常感到压力山大。在这种情况下,ChatGPT应运而生…...

AI与Python共舞:如何利用深度学习优化推荐系统?
AI与Python共舞:如何利用深度学习优化推荐系统? 当你在浏览新闻、电影或是购物平台时,那些仿佛读懂你心思的个性化推荐背后,正是AI技术与Python语言的精妙协作。今天,我们将通过一个实际案例,探索如何利用…...

URLSearchParams: 浏览器中的查询字符串处理利器
一、 概述 在Web开发中,处理URL的查询字符串是一个常见任务。URLSearchParams API 提供了一种简单而强大的方法来处理Web URL的查询参数。它是一个内置的浏览器API,允许你以名称/值对的形式轻松地创建、读取、更新和删除查询参数。 二、URLSearchParam…...
2024最新初级会计职称题库来啦!!!
16.根据增值税法律制度的规定,下列各项中,属于"提供加工、修理修配劳务"的是()。 A.修理小汽车 B.修缮办公楼 C.爆破 D.矿山穿孔 答案:A 解析:选项AB:修理有形动产(…...

Stirling PDF 部署 - 强大的PDF Web在线编辑工具箱
简介 这是一个强大的、可本地托管的、基于 Web 的 PDF 操作工具,可使用 Docker部署。它使您能够对 PDF 文件执行各种操作,包括拆分、合并、转换、重组、添加图像、旋转、压缩等。这个本地托管的 Web 应用程序已经发展到包含一套全面的功能,可…...
)
大数据面试题之MapReduce(3)
目录 reduce任务什么时候开始? MapReduce的reduce使用的是什么排序? MapReduce怎么确定MapTask的数量? Map数量由什么决定 MapReduce的map进程和reducer进程的ivm垃圾回收器怎么选择可以提高吞吐量? MapReduce的task数目划分 MapReduce作业执行的过程中,中…...

[leetcode]squares-of-a-sorted-array. 有序数组的平方
. - 力扣(LeetCode) class Solution { public:vector<int> sortedSquares(vector<int>& nums) {int n nums.size();vector<int> ans(n);for (int i 0, j n - 1, pos n - 1; i < j;) {if (nums[i] * nums[i] > nums[j] *…...

使用Spring Boot和Spring Data JPA进行数据库操作
使用Spring Boot和Spring Data JPA进行数据库操作 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在现代的Web应用开发中,数据库操作是不可或缺的一…...
《昇思25天学习打卡营第17天 | 昇思MindSporeCycleGAN图像风格迁移互换》
17天 本节学习了CycleGAN图像风格迁移互换。 CycleGAN即循环对抗生成网络,该模型实现了一种在没有配对示例的情况下学习将图像从源域 X 转换到目标域 Y 的方法。该模型一个重要应用领域是域迁移,可以通俗地理解为图像风格迁移。其实在 CycleGAN 之前&a…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
