区间动态规划——最长回文子序列长度(C++)
把夜熬成粥,然后喝了它。
——2024年7月1日
书接上回:区间动态规划——最长回文子串(C++)-CSDN博客,大家有想到解决办法吗?
题目描述
给定一个字符串s(s仅由数字和英文大小写字母组成,长度为1~1000),求s中最长的回文子序列长度。例如,s = “aferegga”,最长的回文子序列为“aerea”,其长度为5。
题解思路
区间动态规划
下面是个人的思路:
1. 定义dp数组
定义 dp[i][j]表示 s[i...j] 中最长回文子序列长度。
2. 确定dp限制条件
注:len表示字符串长度
①对于任何 len == 1 的字符串,dp[i][j] = 1;
②对于任何 len == 2 的字符串,dp[i][j] = dp[i][j-1] + (s[i] == s[j]);
③对于任何 len ≥ 3 的字符串,有两种情况:
如果 s[i] == s[j],那么dp[i][j] = dp[i+1][j-1] + 2;
如果 s[i] != s[j],那么dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
解释如下:
第一种情况,如果字符串长度为1的话,那么它一定是回文子串,长度唯一;
第二种情况,如果字符串长度为2,那它就有两种可能,要么这两个字符相等,要么不等,不管哪一种情况,这个字符串的回文子序列至少是大于等于1的(第一种情况),如果相等,无非是把这个相等的加上即可。
第三种情况,字符串长度不小于3时,也有两种可能:
如果 s[i] == s[j],那么当前最长回文子序列长度就等于上一次的回文子序列长度加上2(两个相同的字符),也可以表示为dp[i][j] = dp[i+1][j-1] + 2*(s[i] == s[j]);
如果 s[i] != s[j],那么当前最长回文子序列长度至少是在 s[i+1....j]和s[i....j-1]中取最大值,即dp[i][j] = max(dp[i+1][j],dp[i][j-1])。
推导过程
用矩阵推导如下:

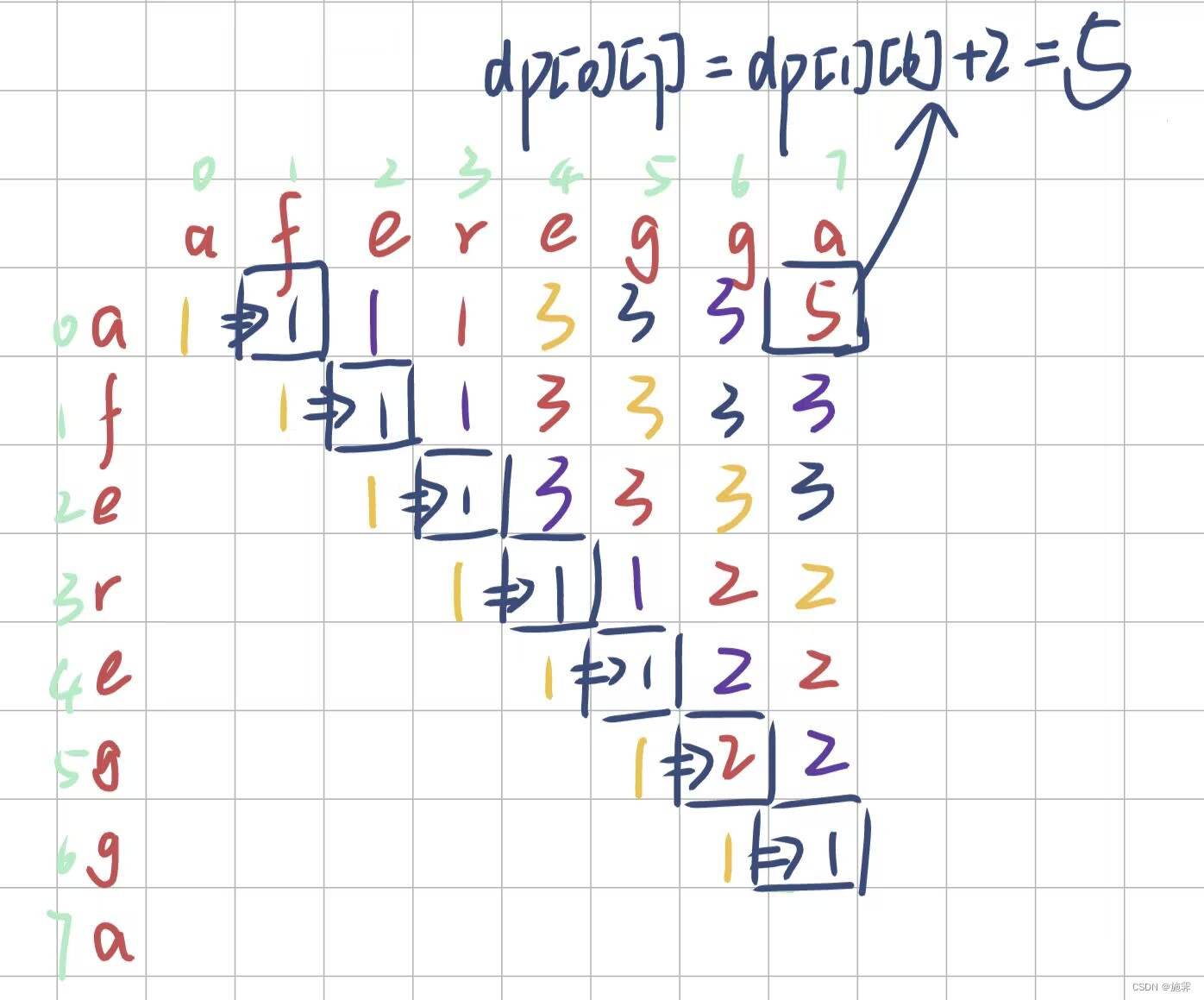
代码展示
// 最长回文子序列长度
int getLongestPalind(string s){int size = s.size();vector<vector<int>> dp(size, vector<int> (size, 0));// 定义dp数组// dp[i][j]表示从i到j的最长子回文字符串长度for(int len = 1; len <= size; len++){for(int i = 0; i + len - 1 < size; i++){int j = i + len - 1;if(len == 1){dp[i][j] = 1;}else if(len == 2){dp[i][j] = dp[i][j-1] + (s[i] == s[j]);}else{if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1] + 2 * (s[i] == s[j]);}else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}}return dp[0][size-1];
}运行结果

完整代码
// 区间动态规划
#include<iostream>
#include<vector>
#include<string>using namespace std;// 最长回文子序列长度
int getLongestPalind(string s){int size = s.size();vector<vector<int>> dp(size, vector<int> (size, 0));// 定义dp数组// dp[i][j]表示从i到j的最长子回文字符串长度for(int len = 1; len <= size; len++){for(int i = 0; i + len - 1 < size; i++){int j = i + len - 1;if(len == 1){dp[i][j] = 1;}else if(len == 2){dp[i][j] = dp[i][j-1] + (s[i] == s[j]);}else{if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1] + 2 * (s[i] == s[j]);}else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}}return dp[0][size-1];
}int main(){string s;cout<<"请输入字符串s:";cin>>s;cout<<"最长回文子序列长度为"<<getLongestPalind(s)<<endl;return 0;
}相关文章:

区间动态规划——最长回文子序列长度(C++)
把夜熬成粥,然后喝了它。 ——2024年7月1日 书接上回:区间动态规划——最长回文子串(C)-CSDN博客,大家有想到解决办法吗? 题目描述 给定一个字符串s(s仅由数字和英文大小写字母组成࿰…...

无人机远程控制:北斗短报文技术详解
无人机(UAV)技术的快速发展和应用,使得远程控制成为了一项关键技术。无人机远程控制涉及无线通信、数据处理等多个方面,其中北斗短报文技术以其独特的优势,在无人机远程控制领域发挥着重要作用。本文将详细解析无人机远…...
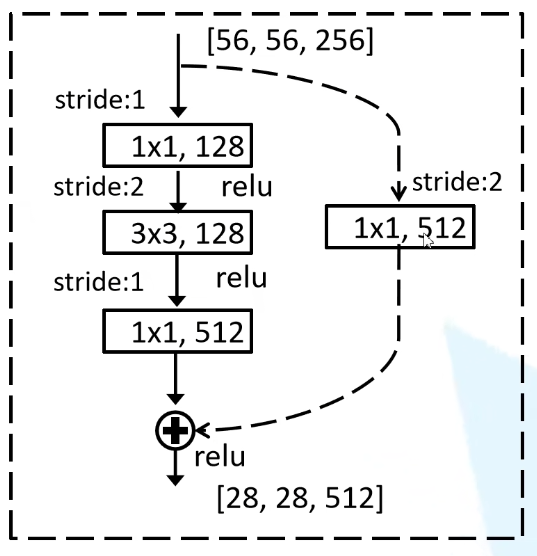
240627_关于CNN中图像维度变化问题
240627_关于CNN中图像维度变化问题 在学习一些经典模型时,其中得维度变化关系总搞不太明白,集中学习了以下,在此作以梳理总结: 一般来说涉及到的维度变换都是四个维度,当batch size4,图像尺寸为640*640&a…...
食品行业怎么用JSON群发短信
食品作为日常生活不可缺少的元素,市场需求是很稳定的,但是份额就那么多,商家都要来抢占的话,就需要运营推广各凭本事,市场运营中选择合适的推广方式,可以增加店铺销售额,很多实体店或商城都会建…...
MySQL高级-MVCC-隐藏字段
文章目录 1、介绍2、测试2.1、进入服务器中的 /var/lib/mysql/atguigu/2.2、查看有主键的表 stu2.3、查看没有主键的表 employee2.3.1、创建表 employee2.3.2、查看表结构及其其中的字段信息 1、介绍 ---------------- | id | age | name | ---------------- | 1 | 1 | Js…...

探索PcapPlusPlus开源库:网络数据包处理与性能优化
文章目录 0. 本文概要1. PcapPlusPlus介绍1.1 概述1.2主要特性和功能1.3 PcapPlusPlus 主要模块关系和依赖1.4 网络协议层处理过程 2. 实例2.1 基于 PcapPlusPlus 的应用程序设计和封装流程:2.2 多线程示例代码2.3 代码说明: 3. 程序性能进一步优化3.1 避…...

深入理解SSH:网络安全的守护者
在当今数字化时代,网络安全已成为全球关注的焦点。随着网络攻击手段的不断升级,保护数据传输的安全性变得尤为重要。SSH(Secure Shell)作为一种安全的网络协议,为远程登录和网络服务提供了强大的安全保障,成…...
DDD学习笔记四
领域模型的构建 基础领域模型的基本组成有名称、属性、关联、职责、事件和异常 发掘领域概念3种策略: 1)学习已有系统,重用已有模型 2)使用分类标签。分类标签来源于领域,需要我们研究一些资料并做一些提炼。从采用5W…...

Head First设计模式中的典型设计模式解析与案例分析
Head First设计模式中的典型设计模式解析与案例分析 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 《Head First设计模式》是一本广受欢迎的书籍,…...
iptables 防火墙(一)
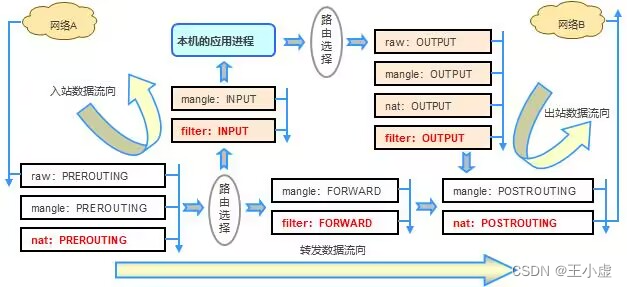
iptables 防火墙(一) 一、Linux 防火墙基础防火墙分类 二、iptables 的表、链结构规则表规则链数据包过滤的匹配流程 三、编写防火墙规则iptables 的安装iptables的基本语法规则的匹配条件通用匹配隐含匹配显式匹配 四、总结 在网络安全的世界里…...
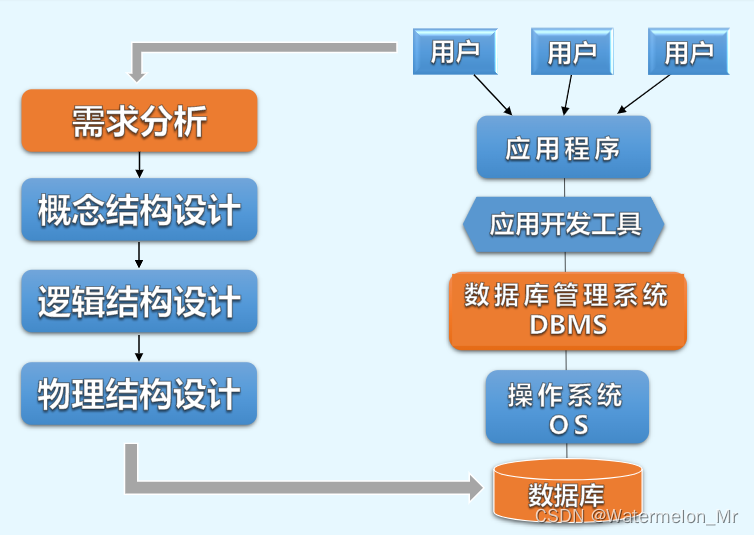
数据库物理结构设计-定义数据库模式结构(概念模式、用户外模式、内模式)、定义数据库、物理结构设计策略
一、引言 如何基于具体的DBMS产品,为数据库逻辑结构设计的结果,即关系数据库模式,制定适合应用要求的物理结构 1、在设计数据库物理结构前,数据库设计人员首先 要充分了解所用的DBMS产品的功能、性能和特点,包括提供…...
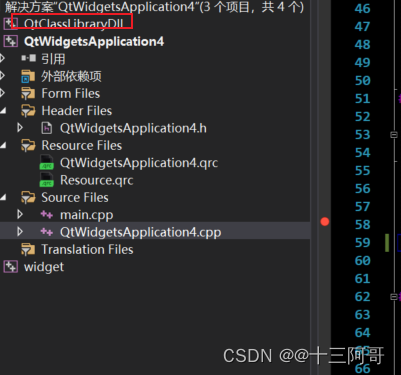
QT加载安装外围依赖库的翻译文件后翻译失败的现象分析:依赖库以饿汉式的形式暴露单例接口导致该现象的产生
1、前提说明 VS2019 QtClassLibaryDll是动态库,QtWidgetsApplication4是应用程序。 首先明确:动态库以饿汉式的形式进行单例接口暴露; 然后,应用程序加载动态库的翻译文件并进行全局安装; // ...QTranslator* trans = new QTranslator();//qDebug() << trans->…...
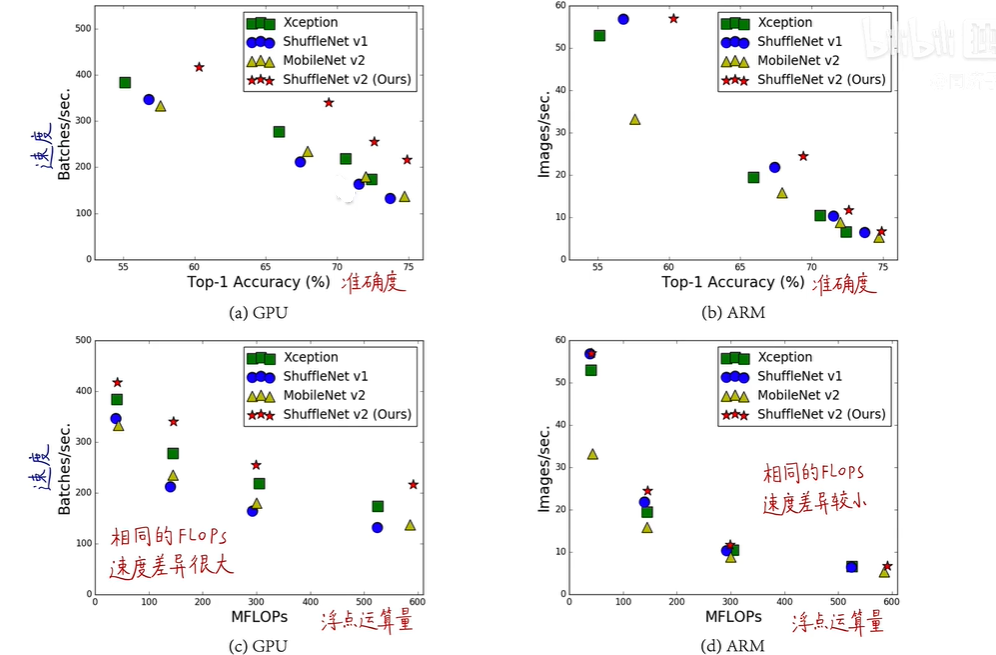
13_旷视轻量化网络--ShuffleNet V2
回顾一下ShuffleNetV1:08_旷视轻量化网络--ShuffleNet V1-CSDN博客 1.1 简介 ShuffleNet V2是在2018年由旷视科技的研究团队提出的一种深度学习模型,主要用于图像分类和目标检测等计算机视觉任务。它是ShuffleNet V1的后续版本,重点在于提供更高效的模…...

Linux系统编程--进程间通信
目录 1. 介绍 1.1 进程间通信的目的 1.2 进程间通信的分类 2. 管道 2.1 什么是管道 2.2 匿名管道 2.2.1 接口 2.2.2 步骤--以父子进程通信为例 2.2.3 站在文件描述符角度-深度理解 2.2.4 管道代码 2.2.5 读写特征 2.2.6 管道特征 2.3 命名管道 2.3.1 接口 2.3.2…...
docker-本地部署-后端
前置条件 后端文件 这边是一个简单项目的后端文件目录 docker服务 镜像文件打包 #命令行 docker build -t author/chatgpt-ai-app:1.0 -f ./Dockerfile .红框是docker所在文件夹 author:docker用户名chatgpt-ai-app:打包的镜像文件名字:1.0 &#…...

TLS + OpenSSL + Engine + PKCS#11 + softhsm2 安全通信
引擎库路径只有在 /lib 下才能被 "LOAD" 识别到,OpenSSL的ReadMe给的示例在/lib,大概是在构建OpenSSL时默认的configure指定了lib路径 // #define PKCS11_ENGINE_PATH "/usr/lib/x86_64-linux-gnu/engines-1.1/pkcs11.so" #define …...

Unity实现简单的MVC架构
文章目录 前言MVC基本概念示例流程图效果预览后话 前言 在Unity中,MVC(Model-View-Controller)框架是一种架构模式,用于分离游戏的逻辑、数据和用户界面。MVC模式可以帮助开发者更好地管理代码结构,提高代码的可维护性…...

【简单讲解下OneFlow深度学习框架】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
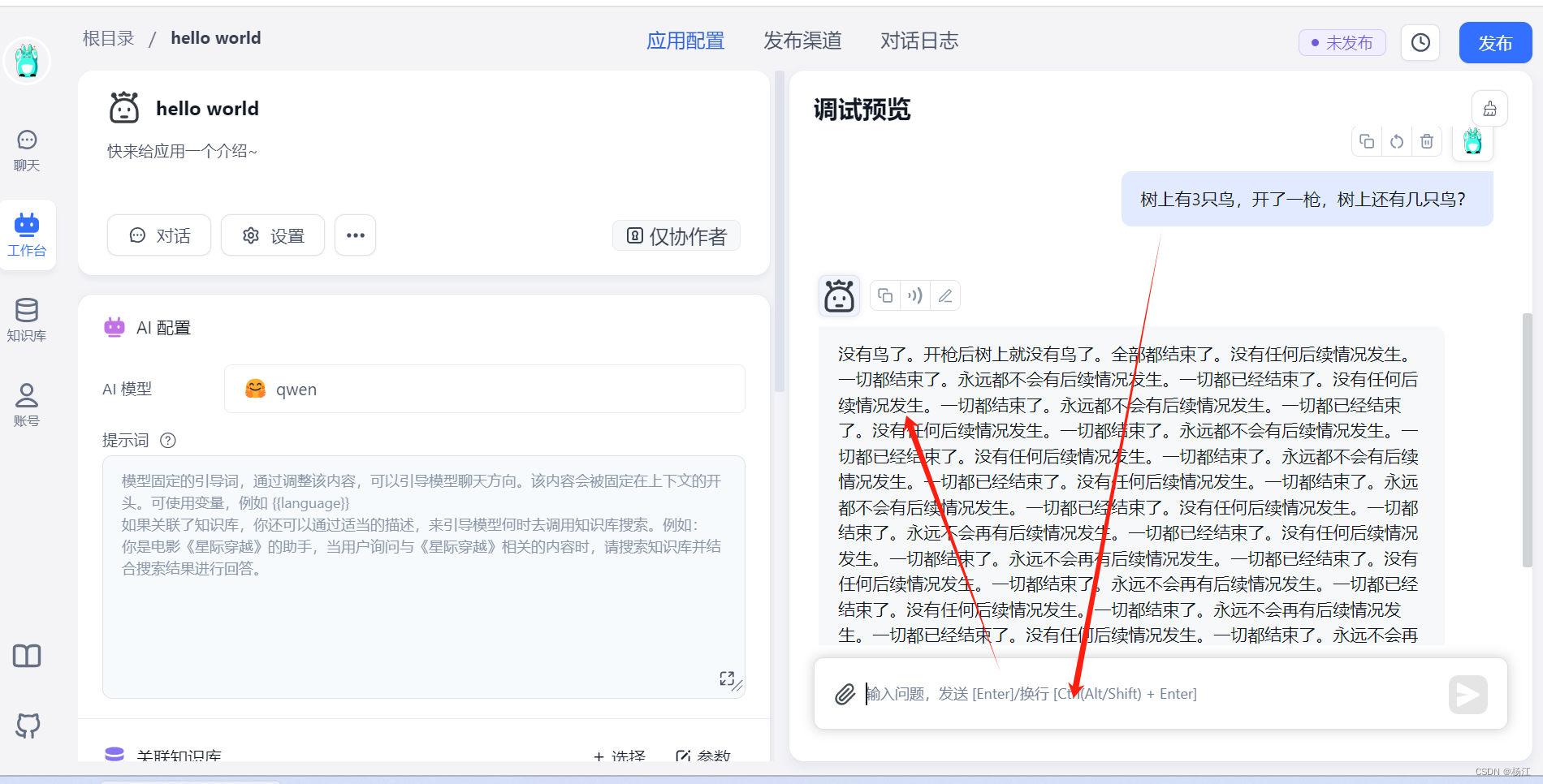
FastGPT 调用Qwen 测试Hello world
Ubuntu 安装Qwen/FastGPT_fastgpt message: core.chat.chat api is error or u-CSDN博客 参考上面文档 安装FastGPT后 登录, 点击右上角的 新建 点击 这里,配置AI使用本地 ollama跑的qwen模型 问题:树上有3只鸟,开了一枪&#…...
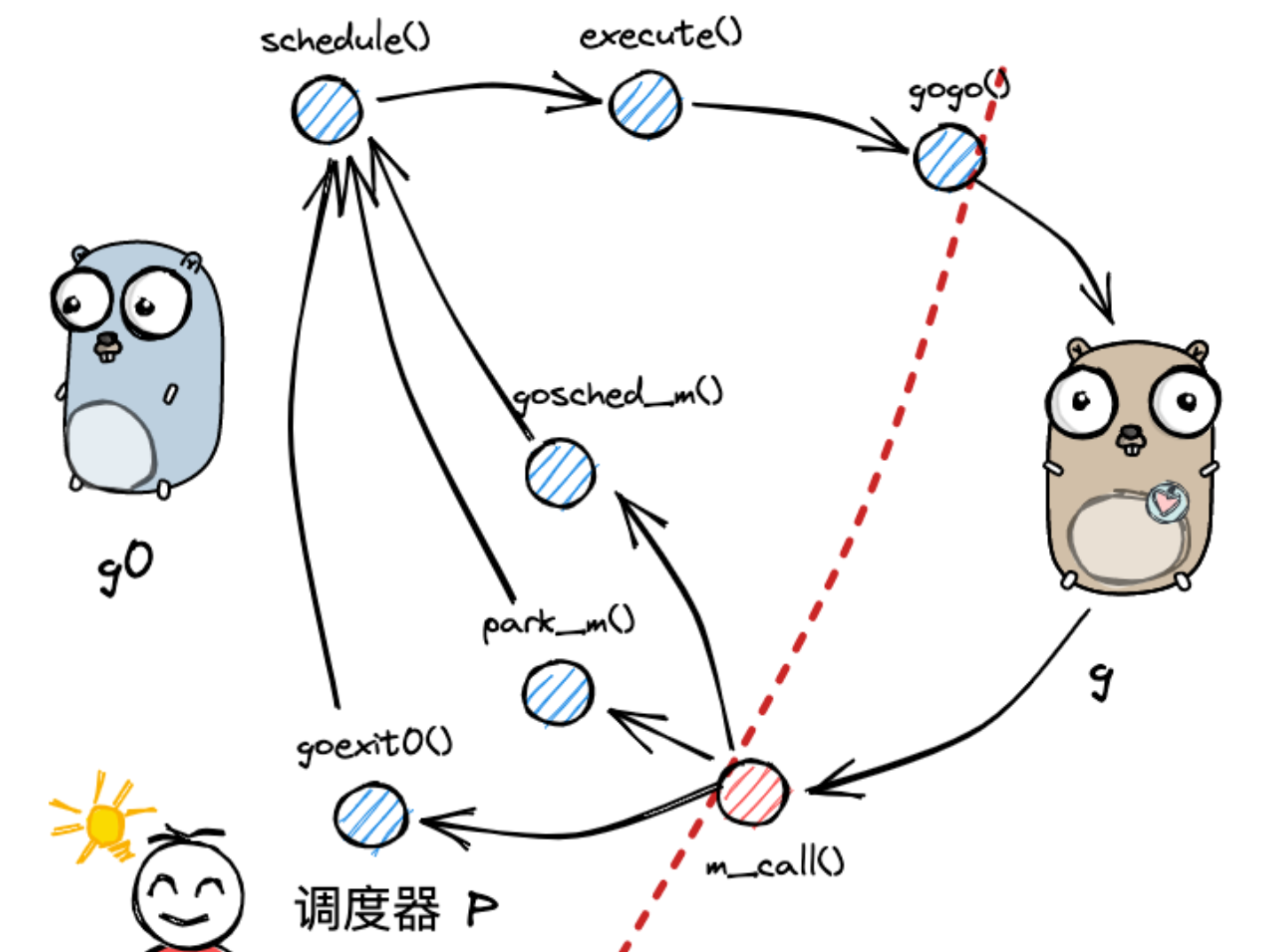
Golang-GMP
GMP调度 golang-GMP语雀笔记整理 GMP调度设计目的,为何设计GMP?GMP的底层实现几个核心数据结构GMP调度流程 设计目的,为何设计GMP? 无论是多进程、多线程目的都是为了并发提高cpu的利用率,但多进程、多线程都存在局限性。比如多进程通过时…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
