IMU 积分的误差状态空间方程推导
文章目录
- 0. 前言
- 1. 离散时间的IMU运动学方程
- 2. 状态变量定义
- 3. 补充公式
- 4. IMU误差状态空间方程推导
0. 前言
本文推导的是 IMU 积分的误差状态空间方程,预积分的推导要比积分复杂,但是推到方法和本文是一样的,因此这里只给出积分的推导方式。
另外,本文的推导方式参考了 R2Live Supplementary Material 中给出的推导,这种方法是基于李群李代数使用 全增量 的方法计算误差状态空间方程,非常好理解。
1. 离散时间的IMU运动学方程
{pi+1=pi+viΔt+12[Ri(ami−bai−nai)−g]Δt2vi+1=vi+[Ri(ami−bai−nai)−g]ΔtRi+1=Riexp[(ωmi−bωi−nωi)Δt]bωi+1=bωi+nbωiΔtbai+1=bai+nbaiΔt\left\{\begin{array}{l} \mathbf{p}_{i+1}=\mathbf{p}_i+\mathbf{v}_i \Delta t+\frac{1}{2}\left[\mathbf{R}_i\left(\mathbf{a}_{m i}-\mathbf{b}_{a_i}-\mathbf{n}_{a i}\right)-\mathbf{g}\right] \Delta t^2 \\ \mathbf{v}_{i+1}=\mathbf{v}_i+\left[\mathbf{R}_i\left(\mathbf{a}_{m i}-\mathbf{b}_{a i}-\mathbf{n}_{a i}\right)-\mathbf{g}\right] \Delta t \\ \mathbf{R}_{i+1}=\mathbf{R}_i \exp \left[\left(\mathbf{\omega}_{mi}-\mathbf{b}_{\omega i}-\mathbf{n}_{\omega i}\right) \Delta t\right] \\ \mathbf{b}_{\omega i+1}=\mathbf{b}_{\omega i}+\mathbf{n}_{b_\omega i} \Delta t \\ \mathbf{b}_{a_i+1}=\mathbf{b}_{a i}+\mathbf{n}_{b_a i} \Delta t \end{array}\right. ⎩⎨⎧pi+1=pi+viΔt+21[Ri(ami−bai−nai)−g]Δt2vi+1=vi+[Ri(ami−bai−nai)−g]ΔtRi+1=Riexp[(ωmi−bωi−nωi)Δt]bωi+1=bωi+nbωiΔtbai+1=bai+nbaiΔt
- 式中忽略了参考坐标系,一般可以选择 worldworldworld 系 W{W}W,此时 g=[0,0,9.8]Tg=[0, 0, 9.8]^Tg=[0,0,9.8]T;
- nai,nωi\mathbf{n}_{a i},\mathbf{n}_{\omega i}nai,nωi 为IMU读数的高斯白噪声;
- nbai,nbωi\mathbf{n}_{b_a i},\mathbf{n}_{b_\omega i}nbai,nbωi 为IMU零偏的随机游走的高斯分布。
2. 状态变量定义
- 名义状态 x^\hat{\mathbf{x}}x^:估计出来的状态,真正能算出来的状态;
- 真实状态 x\mathbf{x}x:无法计算出来的状态,永远不知道的状态,只能用公式表示出来;
- 误差状态 δx\mathbf{\delta x}δx:真实状态 x\mathbf{x}x 与 名义状态 x^\hat{\mathbf{x}}x^ 的差值,关系式为:x=x^+δx\mathbf{x} = \hat{\mathbf{x}} + \mathbf{\delta x}x=x^+δx,即 真实状态 = 名义状态 + 误差状态。
比如:
-
角速度 ω\mathbf{\omega}ω 的名义状态和真实状态:
{名义值:ωi^=ωmi−b^ωi真实值:ωi=ωi^−δb^ωi−nωi=ωmi−b^ωi−δb^ωi−nωi\left\{\begin{array}{l} 名义值:\hat{\mathbf{\omega}_i} = \mathbf{\omega}_{m i} - \hat{\mathbf{b}}_{\omega i} \\ 真实值:\mathbf{\omega}_i = \hat{\mathbf{\omega}_i} - \delta\hat{\mathbf{b}}_{\omega i} - \mathbf{n}_{\omega i} = \mathbf{\omega}_{m i} - \hat{\mathbf{b}}_{\omega i} - \delta\hat{\mathbf{b}}_{\omega i} - \mathbf{n}_{\omega i} \end{array}\right. {名义值:ωi^=ωmi−b^ωi真实值:ωi=ωi^−δb^ωi−nωi=ωmi−b^ωi−δb^ωi−nωi -
加速度 a\mathbf{a}a 的名义状态和真实状态:
{名义值:ai^=ami−b^ai真实值:ai=ai^−δb^ai−nai=ami−b^ai−δb^ai−nai\left\{\begin{array}{l} 名义值:\hat{\mathbf{a}_i} = \mathbf{a}_{m i} - \hat{\mathbf{b}}_{a i} \\ 真实值:\mathbf{a}_i = \hat{\mathbf{a}_i} - \delta\hat{\mathbf{b}}_{a i} - \mathbf{n}_{a i} = \mathbf{a}_{m i} - \hat{\mathbf{b}}_{a i} - \delta\hat{\mathbf{b}}_{a i} - \mathbf{n}_{a i} \end{array}\right. {名义值:ai^=ami−b^ai真实值:ai=ai^−δb^ai−nai=ami−b^ai−δb^ai−nai
3. 补充公式
-
李代数上的增量和李群上的扰动之间的关系:
exp(ϕ+Δϕ)=exp(JlΔϕ)⋅exp(ϕ)=exp(ϕ)⋅exp(JrΔϕ)\begin{align} \exp (\phi+\Delta \phi) =\exp (J_l \Delta \phi) \cdot \exp (\phi) =\exp (\phi) \cdot \exp (J_r \Delta \phi)\end{align} exp(ϕ+Δϕ)=exp(JlΔϕ)⋅exp(ϕ)=exp(ϕ)⋅exp(JrΔϕ) -
SO(3)SO(3)SO(3)的伴随性质:
R⊤exp(ϕ)R=exp(R⊤ϕ)\begin{align}R^{\top} \exp (\phi) R=\exp \left(R^{\top} \phi\right)\end{align} R⊤exp(ϕ)R=exp(R⊤ϕ) -
BCH近似公式:
log[exp(ϕ1)exp(ϕ2)]={Jl(ϕ2)−1ϕ1+ϕ2,ϕ1≈0Jr(ϕ1)−1ϕ2+ϕ1,ϕ2≈0\begin{align} \log \left[\exp \left(\phi_1\right) \exp \left(\phi_2\right)\right]=\left\{\begin{array}{l}\operatorname{J_l}\left(\phi_2\right)^{-1} \phi_1+\phi_2, \quad \phi_1 \approx 0 \\ \operatorname{J_r}\left(\phi_1\right)^{-1} \phi_2+\phi_1, \quad \phi_2 \approx 0 \end{array}\right.\end{align} log[exp(ϕ1)exp(ϕ2)]={Jl(ϕ2)−1ϕ1+ϕ2,ϕ1≈0Jr(ϕ1)−1ϕ2+ϕ1,ϕ2≈0
4. IMU误差状态空间方程推导
4.1. 旋转误差 δr^i+1\delta\hat{\mathbf{r}}_{i+1}δr^i+1
定义:δr^i+1=log[R^i+1⊤Ritt]名义值:R^i+1=R^iexp(w^iΔt)真实值:Ri+1=R^iexp(δr^i)⋅exp(ωiΔt)\begin{aligned} \text { 定义:} \delta \hat{r}_{i+1} & =\log \left[\hat{R}_{i+1}^{\top} R_{i t t}\right] \\ \text {名义值:} \hat{R}_{i+1} & =\hat{R}_i \exp \left(\hat{w}_i \Delta t\right) \\ \text {真实值:} R_{i+1} & =\hat{R}_i \exp \left(\delta \hat{r}_i\right) \cdot \exp \left(\omega_i \Delta t\right) \end{aligned} 定义:δr^i+1名义值:R^i+1真实值:Ri+1=log[R^i+1⊤Ritt]=R^iexp(w^iΔt)=R^iexp(δr^i)⋅exp(ωiΔt)
则旋转误差如下:

4.2. 速度误差 δv^i+1\delta\hat{\mathbf{v}}_{i+1}δv^i+1
名义值:v^i+1=v^i+(R^ia^i−g)Δt真实值:vi+1=(v^i+δv^i)+[R^iexp(δr^i)(a^i−δb^ai−nai)−g]Δt\begin{aligned} 名义值: \hat{v}_{i+1}&=\hat{v}_i+\left(\hat{R}_i \hat{a}_i-g\right) \Delta t \\ 真实值:v_{i+1} &= \left(\hat{v}_i+\delta \hat{v}_i \right) + \left[\hat{R}_i \exp \left(\delta \hat{r}_i\right)\left(\hat{a}_i-\delta \hat{b}_{a i}-n_{a i}\right)-g\right] \Delta t \end{aligned} 名义值:v^i+1真实值:vi+1=v^i+(R^ia^i−g)Δt=(v^i+δv^i)+[R^iexp(δr^i)(a^i−δb^ai−nai)−g]Δt

4.3. 平移误差 δpi+1\delta \mathbf{p}_{i+1}δpi+1
名义值: p^i+1=pi^+v^iΔt+12(Ri^ai^−g)Δt2真实值: pi+1=(p^i+δp^i)+(v^i+δv^i)Δt+12[R^i⋅exp(δr^i)(a^i−δb^ai−nai)−g]⋅Δt2\begin{aligned} & \text { 名义值: } \hat{p}_{i+1}=\hat{p_i}+\hat{v}_i \Delta t+\frac{1}{2}\left(\hat{R_i} \hat{a_i}-g\right) \Delta t^2 \\ & \text { 真实值: } p_{i+1}=\left(\hat{p}_i+\delta \hat{p}_i\right)+\left(\hat{v}_i+\delta \hat{v}_i\right) \Delta t+\frac{1}{2}\left[\hat{R}_i \cdot \exp \left(\delta \hat{r}_i\right)\left(\hat{a}_i-\delta \hat{b}_{ai}-n_{ai}\right) -g\right] \cdot \Delta t^2 \\ & \end{aligned} 名义值: p^i+1=pi^+v^iΔt+21(Ri^ai^−g)Δt2 真实值: pi+1=(p^i+δp^i)+(v^i+δv^i)Δt+21[R^i⋅exp(δr^i)(a^i−δb^ai−nai)−g]⋅Δt2

4.4. 角速度零偏误差 δb^wi+1\delta \hat{b}_{w_{i+1}}δb^wi+1
名义值:b^wi+1=b^wi真实值:bwi+1=b^wi+δbwi+Δt⋅nbwi误差:δbwi+1=δbwi+Δt⋅nbwi\begin{aligned} \text { 名义值:} \hat{b}_{w_{ i+1}} &=\hat{b}_{w i} \\ \text { 真实值:} b_{w_{i+1} } &=\hat{b}_{w_i}+\delta b_{w i}+\Delta t \cdot n_{b_{wi}} \\ \text { 误差:} \delta b_{w_{i+1} } &=\delta b_{w i}+\Delta t \cdot n_{b_{wi}} \\ \end{aligned} 名义值:b^wi+1 真实值:bwi+1 误差:δbwi+1=b^wi=b^wi+δbwi+Δt⋅nbwi=δbwi+Δt⋅nbwi
4.5. 加速度零偏误差 δb^ai+1\delta \hat{b}_{a_{i+1}}δb^ai+1
名义值:b^ai+1=b^ai真实值:bai+1=b^ai+δbai+Δt⋅nbai误差:δbai+1=δbai+Δt⋅nbai\begin{aligned} \text { 名义值:} \hat{b}_{a_{ i+1}} &=\hat{b}_{a i} \\ \text { 真实值:} b_{a_{i+1} } &=\hat{b}_{a_i}+\delta b_{a i}+\Delta t \cdot n_{b_{ai}} \\ \text { 误差:} \delta b_{a_{i+1} } &=\delta b_{a i}+\Delta t \cdot n_{b_{ai}} \\ \end{aligned} 名义值:b^ai+1 真实值:bai+1 误差:δbai+1=b^ai=b^ai+δbai+Δt⋅nbai=δbai+Δt⋅nbai
4.6. 整理成矩阵状态空间方程的形式
定义IMU运动学的矩阵状态空间方程形式为
δx^i+1=Fx⋅δx^i+Fw⋅wi\delta \hat{\mathbf{x}}_{i+1}=\mathbf{F}_x \cdot \delta \hat{\mathbf{x}}_i + \mathbf{F}_w \cdot \mathbf{w}_i δx^i+1=Fx⋅δx^i+Fw⋅wi
其中状态变量的定义为:
δx^i=[δr^i,δp^i,δv^i,δb^wi,δb^ai]⊤wi=[δnwi,δnai,δnbwi,δnbai]⊤\begin{aligned} \delta \hat{\mathbf{x}}_i &= \left[\delta \hat{\mathbf{r}}_i, ~~\delta \hat{\mathbf{p}}_i, ~~\delta \hat{\mathbf{v}}_i, ~~\delta \hat{\mathbf{b}}_{wi}, ~~\delta \hat{\mathbf{b}}_{ai}\right]^{\top} \\ \mathbf{w}_i &= \left[\delta\mathbf{n}_{wi}, ~~\delta\mathbf{n}_{ai}, ~~\delta\mathbf{n}_{b_{wi}}, ~~ \delta\mathbf{n}_{b_{ai}}\right]^{\top} \end{aligned} δx^iwi=[δr^i, δp^i, δv^i, δb^wi, δb^ai]⊤=[δnwi, δnai, δnbwi, δnbai]⊤
则系数矩阵为:
Fx=[exp(−ωiΔt^)00−IΔt00IIΔt00−R^i(a^i)×Δt0I0−R^iΔt000I000000]Fω=[−IΔt00000000−R^iΔt0000IΔt0000IΔt]\begin{aligned} \mathbf{F}_x &= \left[\begin{array}{ccccc} \exp \left(-\hat{\omega_i \Delta t}\right) & 0 & 0 & -I \Delta t & 0 \\ 0 & I & I \Delta t & 0 & 0\\ -\hat{R}_i\left(\hat{a}_i\right)_{\times} \Delta t & 0 & I & 0 & -\hat{R}_i \Delta t \\ 0 & 0 & 0 & I & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \\\\ F_\omega &=\left[\begin{array}{cccc} -I \Delta t & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & -\hat{R}_i \Delta t & 0 & 0 \\ 0 & 0 & I \Delta t & 0 \\ 0 & 0 & 0 & I \Delta t \end{array}\right] \end{aligned} FxFω=exp(−ωiΔt^)0−R^i(a^i)×Δt000I0000IΔtI00−IΔt00I000−R^iΔt00=−IΔt000000−R^iΔt00000IΔt00000IΔt
协方差矩阵的传播公式为:
Pi+1=FxPiFx⊤+FωQFω⊤\mathbf{P}_{i+1}=\mathbf{F}_x \mathbf{P}_i \mathbf{F}_x{ }^{\top}+\mathbf{F}_\omega \mathbf{Q} \mathbf{F}_\omega{ }^{\top} Pi+1=FxPiFx⊤+FωQFω⊤
其中 Q\mathbf{Q}Q 为测量噪声的协方差矩阵。
相关文章:

IMU 积分的误差状态空间方程推导
文章目录0. 前言1. 离散时间的IMU运动学方程2. 状态变量定义3. 补充公式4. IMU误差状态空间方程推导4.1. 旋转误差 δr^i1\delta\hat{\mathbf{r}}_{i1}δr^i14.2. 速度误差 δv^i1\delta\hat{\mathbf{v}}_{i1}δv^i14.3. 平移误差 δpi1\delta \mathbf{p}_{i1}δpi14.4. …...

VirtualBox的克隆与复制
快照太多,想整合成1个文件怎么办? 最近,我就遇到一个问题。快照太多了。比较占用空间怎么办? 错误做法 一开始,我是这么操作的,选中某个快照,然后选择删除…然后我登录虚拟机后,发…...

每天5分钟玩转机器学习算法:逆向概率的问题是什么?贝叶斯公式是如何解决的?
本文重点 前面我们已经知道了贝叶斯公式,以及贝叶斯公式在机器学习中的应用,那么贝叶斯公式究竟解决了一个什么样的问题呢?贝叶斯是为了解决逆向概率的问题。 正向的概率和逆向的概率 正向概率:假设袋子里面有N个白球,有M个黑球,你伸手一摸,那么问题就是你摸出黑球的概…...

游戏闲聊之游戏是怎么赚钱的
其实一般情况下不太爱写这种文章,简单说就一点,这个行业的人我惹不起。 1、外挂 所谓外挂,是指通过技术手段,提供辅助游戏的工具,方便玩家获得一些额外的能力; 这事我特意咨询过律师,外挂分两…...
Redis高频面试题汇总(下)
目录 1.Redis中什么是Big Key(大key) 2.Big Key会导致什么问题 3.如何发现 bigkey? 4.为什么redis生产环境慎用keys *命令 5.如何处理大量 key 集中过期问题 6.使用批量操作减少网络传输 7.缓存穿透 8.缓存击穿 9.缓存雪崩 10.缓存污染(或满了…...
Windows修改Docker安装目录修改Docker镜像目录,镜像默认存储位置存放到其它盘
Windows安装Docker,默认是安装在C盘,下载镜像后会占用大量空间,这时需要调整镜像目录;场景:不想连服务器或者没有服务器,想在本地调试服务,该需求就非常重要。基于WSL2安装docker后,…...

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
mgre实验
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...
)
一文彻底了解Zookeeper(介绍篇)
zookeeper 是什么? zookeeper是一个分布式协作框架,提供高可用,高性能,强一致等特性 zookeeper 有哪些应用场景? 分布式锁:分布式锁是指在分布式环境中,多个进程或线程需要互斥地访问某个共享…...
1. ELK Stack 理论篇之什么是ELK Stack?
ELK Stack 理论篇之什么是ELK Stack?1.1 什么是 ELK Stack?1.2 ELK Stack的发展史1.2.1 Elasticsearch1.2.2 引入 Logstash 和 Kibana,产品更强大1.2.3 社区越来越壮大,用例越来越丰富1.2.4 然后我们向 ELK 中加入了 Beats1.2.5 那么&#x…...
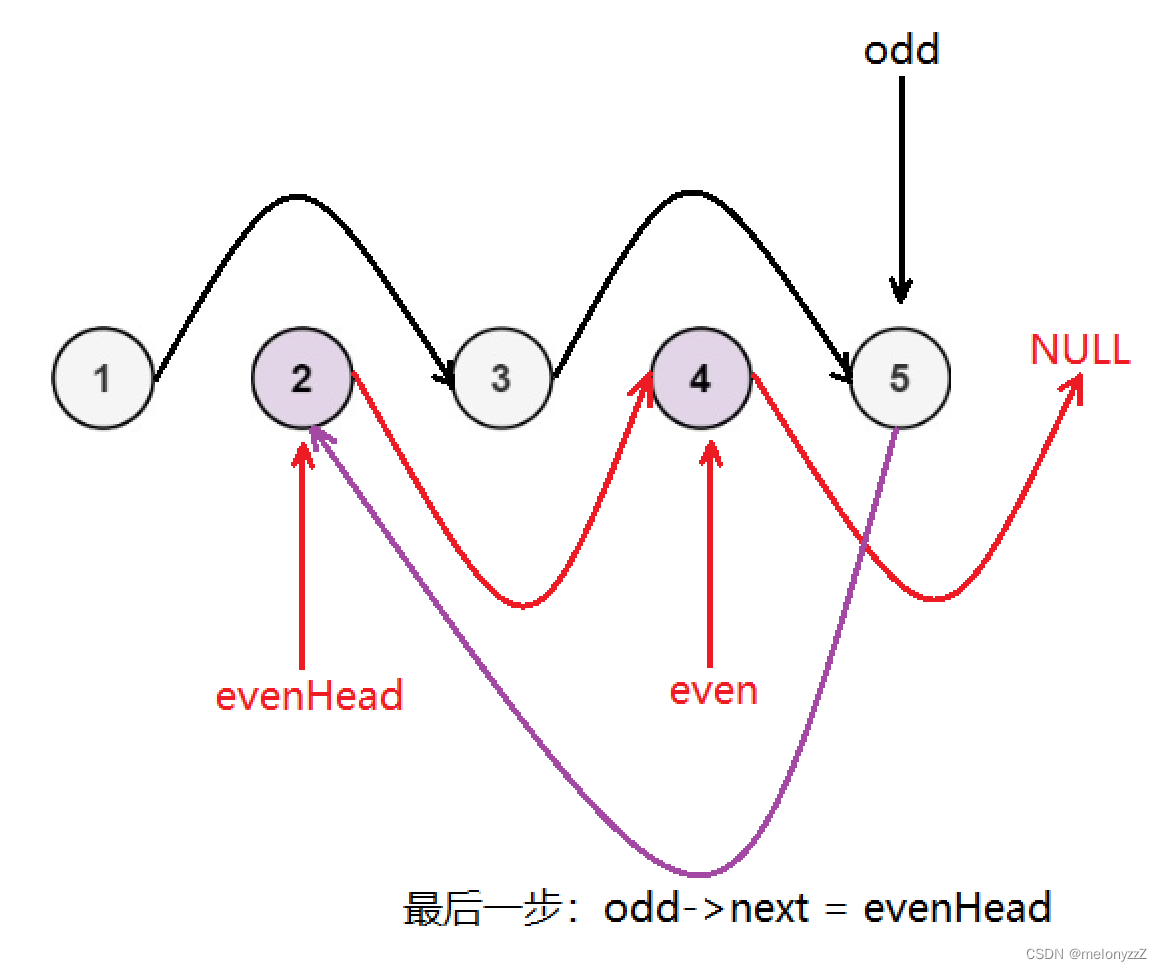
两道有关链表的练习
目录 一、分割链表 二、奇偶链表 一、分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输…...
Python uiautomator2安卓自动化测试
一、前言 uiautomator2是Python对Android设备进行UI自动化的库,支持USB和WIFI链接,可以实现获取屏幕上任意一个APP的任意一个控件属性,并对其进行任意操作。 重点是它可以实现安卓自动化采集,甚至是群控采集,且安装和…...

Leetcode. 160相交链表
文章目录指针解法指针解法 核心思路 : 先 分别求两个链表的长度 然后长的链表先走 差距步(长-短) 最后长链表和短链表同时走 ,第一地址相同的就是交点 ,注意一定是地址相同 不可能出现上图这种情况 ,因为C1…...

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
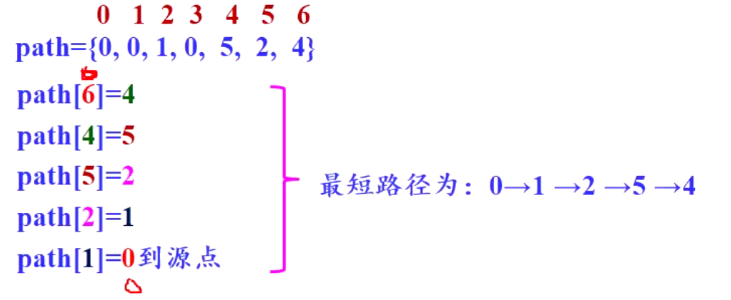
【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
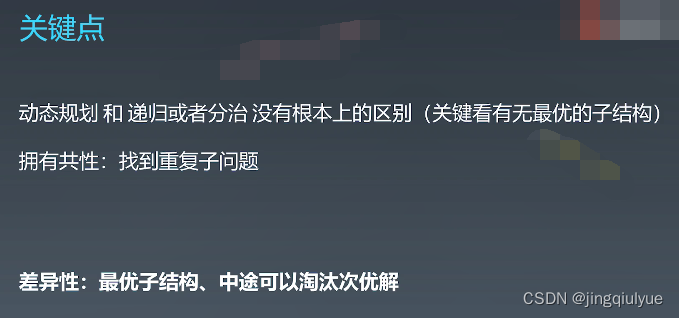
【专项训练】动态规划-3
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
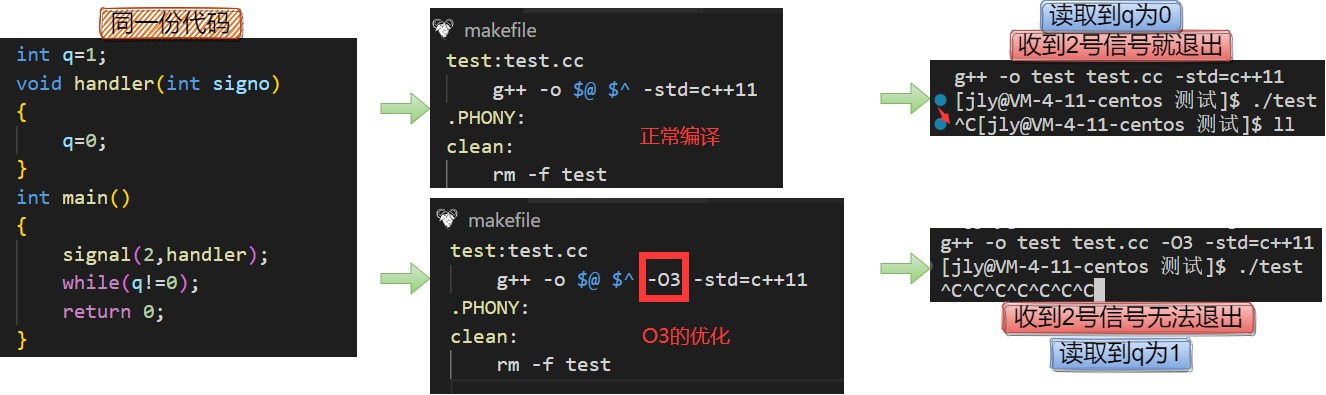
【Linux】信号+再谈进程地址空间
目录 一、Linux中的信号 1、Linux中的信号 2、进程对信号的处理 3、信号的释义 二、信号的捕捉 1、信号的捕捉signal() 2、信号的捕捉sigaction() 三、信号如何产生? 1、kill()用户调用kill向操作系统发送信号 通过命令行参数模仿写一个kill命令 2、rais…...
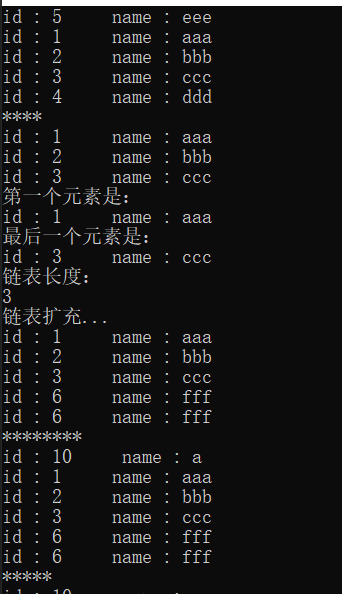
C++回顾(二十一)—— list容器
21.1 list概述 list是一个双向链表容器,可高效地进行插入删除元素。list不可以随机存取元素,所以不支持at.(pos)函数与[]操作符。It(ok) it5(err)需要添加头文件:#include <list> 21.2 list构造 (1)默认构造…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
