DP:子数组问题
文章目录
- 引言
- 子数组问题介绍
- 动态规划的基本概念
- 具体问题的解决方法
- 动态规划解法:
- 关于子数组问题的几个题
- 1.最大子数组和
- 2.环形子数组的最大和
- 3.乘积最大子数组
- 4.乘积为正数的最长子数组长度
- 5.等差数列划分
- 总结

引言
介绍动态规划(DP)在解决子数组问题上的重要性,以及本文的目的——通过具体问题的分析和代码示例,帮助读者理解如何用DP解决子数组问题。
子数组问题介绍
简要介绍什么是子数组问题,以及这些问题在实际应用中的重要性。例如,最大子数组和问题、最长递增子数组问题等。
动态规划的基本概念
解释动态规划的基本思想:通过将问题分解为子问题,保存子问题的解来避免重复计算,从而提高算法效率。可以简单介绍状态、状态转移方程和初始条件等基本概念。
具体问题的解决方法
最大子数组和问题(Maximum Subarray Sum)
问题描述:
给定一个整数数组,找出和最大的连续子数组,并返回其最大和。
动态规划解法:
定义状态:dp[i]表示以第i个元素结尾的最大子数组和。
状态转移方程:dp[i] = max(nums[i], dp[i-1] + nums[i])
即对于第i个元素,最大子数组和要么是自己,要么是前一个元素的最大子数组和加上自己。
初始状态:dp[0] = nums[0]
结果:max(dp),即所有dp[i]中的最大值。
关于子数组问题的几个题
1.最大子数组和
题目链接
题目:
样例输出和输入:
题目要求很简单,就是求出 最长的子数组的和,这个和有一个要求就是和最大。
算法原理:
状态表示:dp[i]表示以i位置为结尾时所有子数组的和中最大的那个。
状态转移方程:
分析:到达i位置时i位置最长的子数组的和应该等于i-1位置的最长子数组的和加上当前i位置的值,还有一种情况:单独分析,就是当前位置的数就是一个子数组,长度为1,所以,dp[i]=max(dp[i-1]+nums[i],nums[i])。
代码展示:
class Solution {
public:int maxSubArray(vector<int>& nums){int n = nums.size();vector<int> dp(n);dp[0] = nums[0];for (int i = 1;i < n;i++){dp[i] = max(dp[i - 1] + nums[i], nums[i]);}int Max = -0x3f3f3f3f;for (int i = 0;i < n;i++){Max = max(dp[i], Max);}return Max;}
};
运行结果:
2.环形子数组的最大和
题目链接
题目:
样例输出和输入:
这道题在第一道题的基础上加了一个条件,就是这是个环形数组头和尾是相连的。也让我们求子数组中和最大的那个。
算法原理:
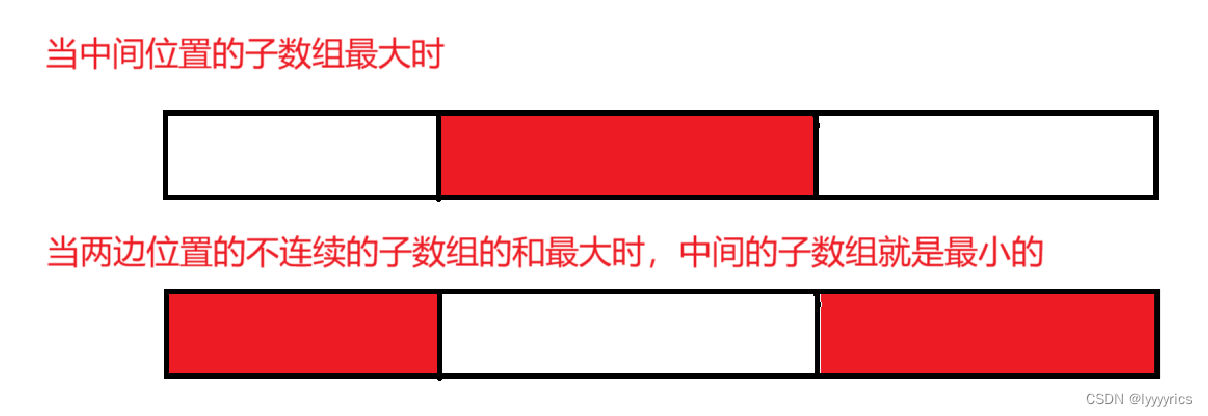
状态表示:分析:明显这道题一个状态是表示不了的,因为这个子数组可能连续也可能不连续,由于求的最大的值,所以第一种情况:当子数组在中间时最大,还有一种情况,子数组在两边时不连续的时候最大 ,当不连续的时候 最大,也就是中间的最小。这两种状态分别为f[i]和g[i]。
状态转移方程:先分析中间最大的时候的状态,当到达i位置的时候i位置的最大的子数组的和就是前一个位置i-1的位置的最大的子数组的和加上当前i位置的值,还有一种情况就是i位置自身成一个长度为1的数组。f[i] = max(f[i - 1] + nums[i-1], nums[i-1]),g[i]也同理,g[i]为当前位置的子数组中最小的那个 子数组的和,所以i位置的子数组和的最小等于前一个位置的子数组和的最小,加上当前位置,g[i - 1] + nums[i-1]最后还要取一个min,g[i] = min(g[i - 1] + nums[i-1], nums[i-1])
代码展示:
class Solution {
public:int maxSubarraySumCircular(vector<int>& nums){int n = nums.size();vector<int> f(n + 1), g(n + 1);int sum = 0;int fmax = INT_MIN;int gmin = INT_MAX;for (int i = 1;i <= n;i++){f[i] = max(f[i - 1] + nums[i-1], nums[i-1]);fmax = max(f[i], fmax);g[i] = min(g[i - 1] + nums[i-1], nums[i-1]);gmin = min(gmin, g[i]);sum += nums[i - 1];}return sum == gmin ? fmax : max(fmax, sum - gmin);}
};
运行结果:

3.乘积最大子数组
题目链接
题目:
样例输出和输入:
这道题的题意和前两道题也大差不差,就是让我们求最大乘积的子数组的乘积。
算法原理:
状态表示:这道题还是需要两个状态,因为有负数情况,不一定是正数乘正数才是最大的,两个负数相乘也 有可能是最大的。f[i]表示以i位置为结尾的子数组中的最大乘积的那个,g[i]表示以i位置为结尾的子数组中最小的乘积的那个。
状态转移方程:首先分析f[i]这个状态,这个状态有三个子状态,第一种状态是i位置是负数时,所以负数应乘上最小的才是最大的,还有一种状态就是当前位置是正数,所以当前位置应该乘上前一个位置中最大的那个子数组的乘积。还有一个情况就是单独成为一个子数组。
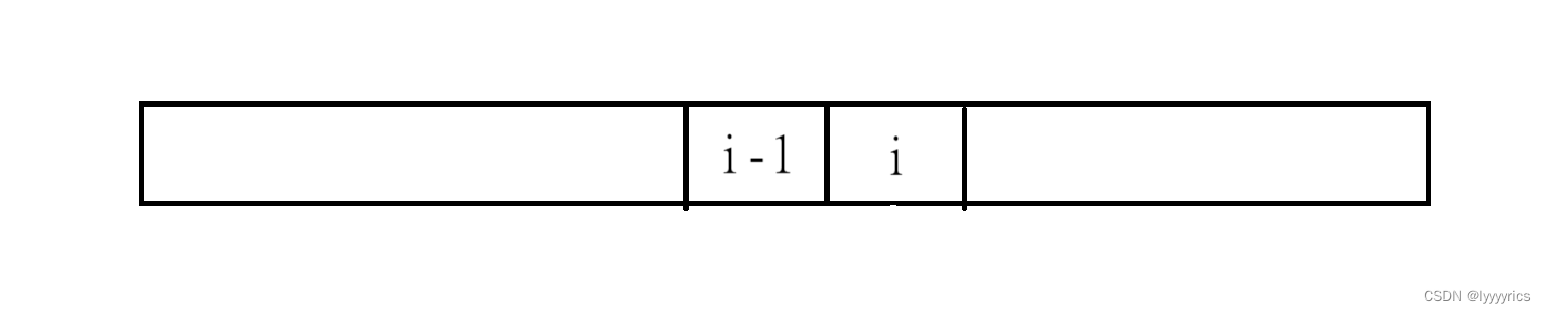
max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))
g[i]的状态转移方程也可以用类似的方法进行分析:min(nums[i - 1], min(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))
代码展示:
class Solution {
public:int maxProduct(vector<int>& nums){int n = nums.size();vector<double> f(n + 1), g(n + 1);//f是最大的,g是最小的g[0] = 1, f[0] = 1;double ret = INT_MIN;for (int i = 1;i <= n;i++){double x = nums[i - 1], y = f[i - 1] * nums[i - 1], z = g[i - 1] * nums[i - 1];f[i] = max(x, max(y, z));g[i] = min(x, min(y, z));ret = max(f[i], ret);}return ret;}
};
运行结果:

4.乘积为正数的最长子数组长度
题目链接
题目:
样例输出和输入:
这道题要求的是乘积是正数的子数组总长度最长的那个子数组的长度。
算法原理:
状态表示:由于两个负数相乘也是正数,所以状态表示的时候我们也要记录负数的状态,f[i]表示以i位置为结尾的所有子数组中乘积是正数的最长的子数组的长度,g[i]]是以i位置为结尾的子数组中乘积为负数的最长子数组的长度。
状态转移方程:需要判断i位置的值是正数还是负数,如果是负数的话就是就需要用前一个位置的负数子数组的最长的那个加一,也就是g[i-1]+1但是前i-1个有可能没有小于零的,所以这里f[i]是有可能是零的,所以这里需要判断一下i-1位置时的g[i-1]的值,当当前值大于零的时候f[i]就等于 前一个位置的f[i-1]+1,同理负数的最长子数组也可以分析出来,状态转移方程:这是大于零的两种状态的情况:g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1,f[i] = f[i - 1] + 1小于零的两种状态的情况:f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1,g[i] = f[i - 1] + 1。
代码展示:
class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();if (n == 1){return nums[0] > 0;}vector<int> f(n), g(n);f[0] = nums[0] > 0, g[0] = nums[0] < 0;int fmax = 0;for (int i = 1;i < n;i++){if (nums[i] > 0){f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;fmax = max(f[i], fmax);}else if (nums[i] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;fmax = max(f[i], fmax);}}return fmax;}
};
运行结果:
5.等差数列划分
题目链接
题目:
样例输出和输入:
这道题题意很简单,就是让我们求所有能构成等差数列的子数组的总和
算法原理:
等差数列性质:2a=c+ba为等差中项。
状态表示:dp[i]为以i位置为结尾的所有子数组中的等差数列的个数。
状态转移方程:先判断i位置的前两个位置是否 满足上述的等差数列的性质:如果满足则dp[i]=dp[i - 1] + 1因为满足,所以dp[i-1]位置需要算上,但是又多了一个子数组,这个子数组 就是满足的那个三个数的子数组。不满足的话,dp[i]直接就是0.
代码展示:
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3){return 0;}vector<int> dp(n);dp[0] = 0, dp[1] = 0;int count = 0;for (int i = 2;i < n;i++){dp[i] = nums[i] + nums[i - 2] == 2 * nums[i - 1] ? dp[i - 1] + 1 : 0;}for(int i=0;i<n;i++){count+=dp[i];}return count;}
};
运行结果:
总结
通过本文的介绍,我们详细探讨了动态规划在解决子数组问题中的应用,具体分析了最大子数组和问题和最长递增子数组问题。这些问题在实际生活中的数据处理、优化等场景中有着广泛的应用。动态规划通过将问题分解为子问题,保存子问题的解,避免了重复计算,从而大大提高了算法的效率。
在学习和应用动态规划的过程中,我们需要明确状态、状态转移方程和初始条件。通过练习具体问题,我们可以更深入地理解动态规划的思想和方法。无论是最大子数组和问题还是最长递增子数组问题,掌握了动态规划的基本原理后,我们可以更灵活地应对其他类似的问题。
希望这篇文章能帮助你更好地理解动态规划在子数组问题中的应用。如果你有任何问题或建议,欢迎在评论区留言,我们将尽力为你解答。祝你在学习动态规划和解决实际问题的过程中取得更多的进步!
相关文章:

DP:子数组问题
文章目录 引言子数组问题介绍动态规划的基本概念具体问题的解决方法动态规划解法:关于子数组问题的几个题1.最大子数组和2.环形子数组的最大和3.乘积最大子数组4.乘积为正数的最长子数组长度5.等差数列划分 总结 引言 介绍动态规划(DP)在解决…...

[Day 20] 區塊鏈與人工智能的聯動應用:理論、技術與實踐
AI在醫療領域的創新應用 隨著科技的快速發展,人工智能(AI)在各行各業的應用越來越廣泛,醫療領域也不例外。AI技術在醫療中的應用不僅提高了診斷的準確性,還改善了病患的治療效果,優化了醫療資源的配置。本…...

Handling `nil` Values in `NSDictionary` in Objective-C
Handling nil Values in NSDictionary in Objective-C When working with Objective-C, particularly when dealing with data returned from a server, it’s crucial (至关重要的) to handle nil values appropriately (适当地) to prevent unexpected crashes. Here, we ex…...

【深入浅出 】——【Python 字典】——【详解】
目录 1. 什么是 Python 字典? 1.1 字典的基本概念 1.2 字典的用途 1.3 字典的优势 2. 字典的基本特点 2.1 键的唯一性 2.2 可变性 2.3 无序性 3. 如何创建字典? 3.1 使用 {} 符号 3.2 使用 dict() 工厂方法 3.3 使用 fromkeys() 方法 4. 字…...

开发RpcProvider的发布服务(NotifyService)
1.发布服务过程 目前完成了mprpc框架项目中的以上的功能。 作为rpcprovider的使用者,也就是rpc方法的发布方 main函数如下: 首先我们init调用框架的init,然后启动一个provider,然后向provider上注册服务对象方法,即us…...

Suno: AI音乐创作的新时代
名人说:一点浩然气,千里快哉风。 ——苏轼 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、什么是Suno?1、Suno2、应用场景二、如何使用Suno制作音乐?步骤1:注册并登录Suno平台步骤2:创建音乐项目步骤3:生成音乐片段三、Suno的影响很高兴你打开了…...

六西格玛项目实战:数据驱动,手机PCM率直线下降
在当前智能手机市场日益竞争激烈的背景下,消费者对手机质量的要求达到了前所未有的高度。PCM(可能指生产过程中的某种不良率或缺陷率)作为影响手机质量的关键因素,直接关联到消费者满意度和品牌形象。为了应对这一挑战,…...
汉诺塔经典问题)
数据结构递归(01)汉诺塔经典问题
说明:使用递归时,必须要遵守两个限制条件: 递归存在限制条件,满⾜这个限制条件时,递归不再继续; 每次递归调⽤之后越来越接近这个限制条件; 1 汉诺塔(Hanoi Tower)经典…...

计算机专业课面试常见问题-计算机网络篇
目录 1. 计算机网络分为哪 5 层? 2. TCP 协议简述? 3. TCP 和 UDP 的区别?->不同的应用场景? 4. 从浏览器输入网址到显示页…...

HarmonyOS ArkUi ArkWeb加载不出网页问题踩坑
使用 使用还是比较简单的,直接贴代码了 别忘了配置网络权限 Entry Component struct WebPage {State isAttachController: boolean falseState url: string State title: string Prop controller: web_webview.WebviewController new web_webview.WebviewCont…...
微信换手机号了怎么绑定新手机号?
微信换手机号了怎么绑定新手机号? 1、在手机上找到并打开微信; 2、打开微信后,点击底部我的,并进入微信设置; 3、在微信设置账号与安全内,找到手机号并点击进入; 4、选择更换手机号,…...

64.WEB渗透测试-信息收集- WAF、框架组件识别(4)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:63.WEB渗透测试-信息收集- WAF、框架组件识别(3)-CSDN博客 我们在…...

java.lang.LinkageError: 链接错误的正确解决方法,亲测有效,嘿嘿,有效
文章目录 问题分析报错原因解决思路解决方法(含代码示例)1. 检查类加载器2. 避免在运行时修改类定义3. 更新或修复 JVM4. 检查应用程序的依赖使用 Maven 检查依赖项使用 Gradle 检查依赖项 java.lang.LinkageError 是 Java 虚拟机在尝试链接类定义时发生…...

python最基础
基本的类 python最基础、最常用的类主要有int整形,float浮点型,str字符串,list列表,dict字典,set集合,tuple元组等等。int整形、float浮点型一般用于给变量赋值,tuple元组属于不可变对象&#…...

Python学习路线图(2024最新版)
这是我最开始学Python时的一套学习路线,从入门到上手。(不敢说精通,哈哈~) 一、Python基础知识、变量、数据类型 二、Python条件结构、循环结构 三、Python函数 四、字符串 五、列表与元组 六、字典与集合 最后再送给大家一套免费…...
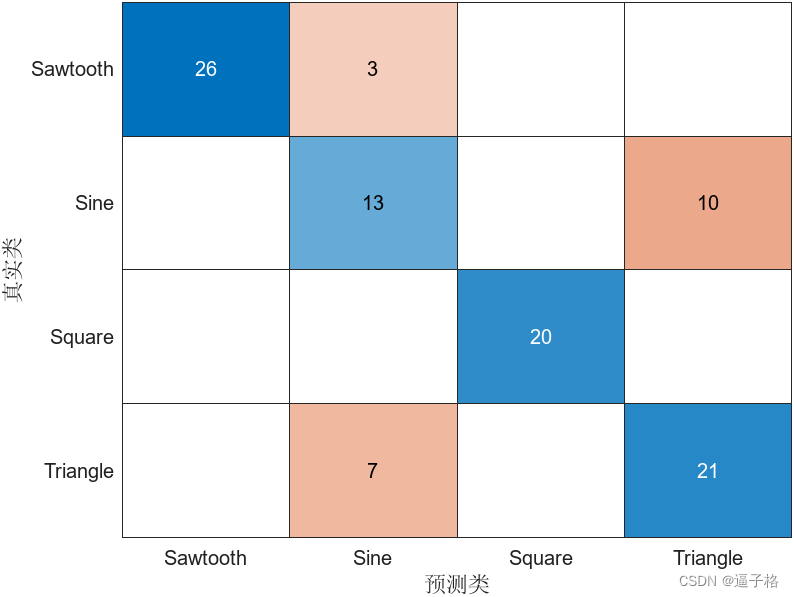
66、基于长短期记忆 (LSTM) 网络对序列数据进行分类
1、基于长短期记忆 (LSTM) 网络对序列数据进行分类的原理及流程 基于长短期记忆(LSTM)网络对序列数据进行分类是一种常见的深度学习任务,适用于处理具有时间或序列关系的数据。下面是在Matlab中使用LSTM网络对序列数据进行分类的基本原理和流…...

RabbitMQ消息可靠性等机制详解(精细版三)
目录 七 RabbitMQ的其他操作 7.1 消息的可靠性(发送可靠) 7.1.1 confim机制(保证发送可靠) 7.1.2 Return机制(保证发送可靠) 7.1.3 编写配置文件 7.1.4 开启Confirm和Return 7.2 手动Ack(保证接收可靠) 7.2.1 添加配置文件 7.2.2 手动ack 7.3 避免消息重复消费 7.3.…...

88888
49615...

深度学习之激活函数
激活函数的公式根据不同的函数类型而有所不同。以下是一些常见的激活函数及其数学公式: Sigmoid函数: 公式:f(x)特性:输出范围在0到1之间,常用于二分类问题,将输出转换为概率值。但存在梯度消失问题&#…...

OpenStack开源虚拟化平台(一)
目录 一、OpenStack背景介绍(一)OpenStack是什么(二)OpenStack的主要服务 二、计算服务Nova(一)Nova组件介绍(二)Libvirt简介(三)Nova中的RabbitMQ解析 OpenS…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...










