归并排序详解(递归与非递归)
归并排序是建立在归并操作上的一种有效算法。该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列间断有序。若将两个有序表合并成一个有序表,成为二路归并。
一、递归实现归并排序
1.算法描述
● 把长度为n的输入序列分成两个长度近似为n/2([begin,mid] [mid + 1,end] )的子序列
● 对这两个子序列再分别进行归并排序,将区间分解到不可在分为止
● 依次将两个排序好的子序列合并成一个最终的排序序列
方法: 开辟新数组,用双指针选出两个子序列中的较小元素尾插在新数组中
2.动图演示
3.核心步骤
(1)图示
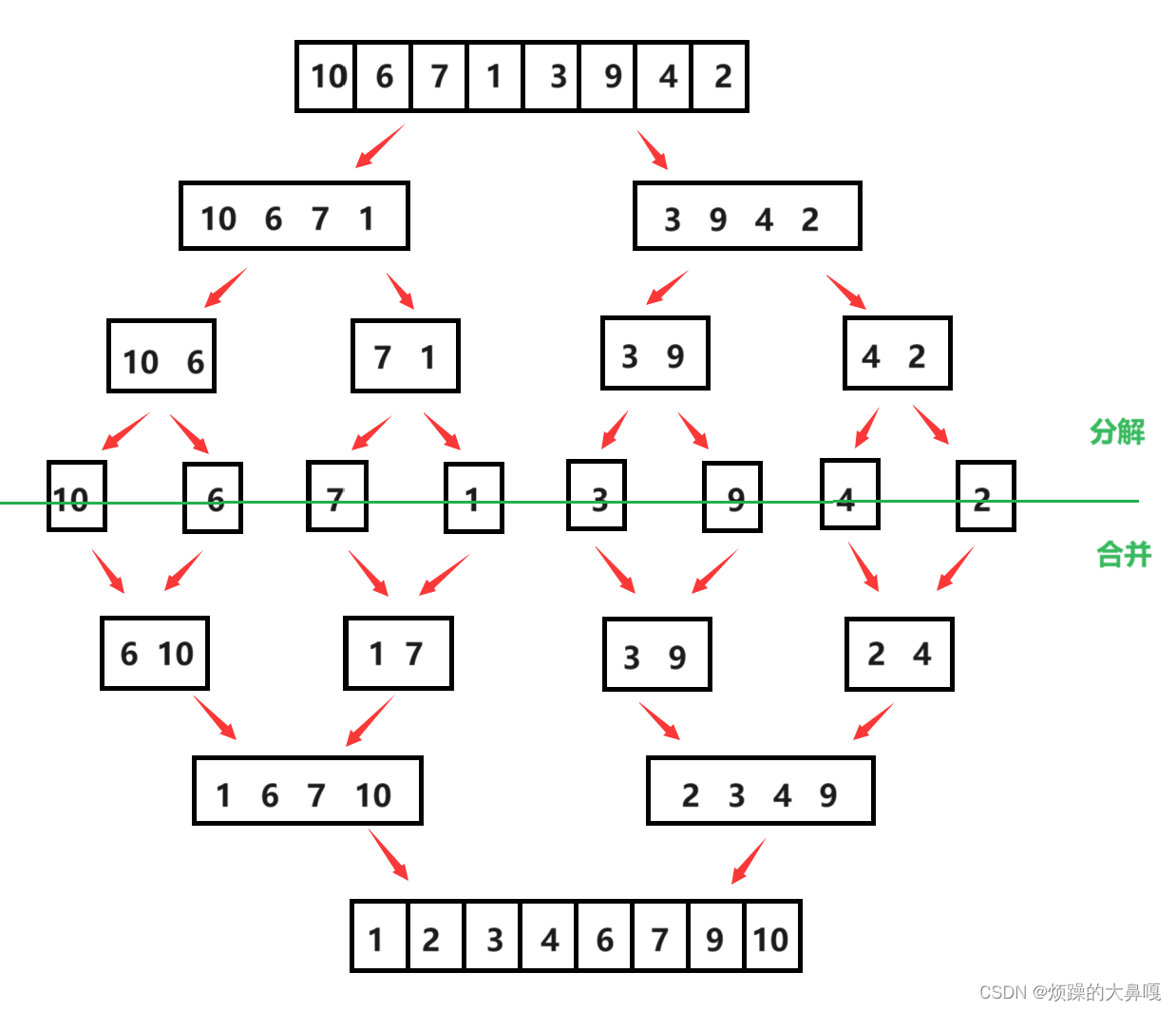
(2)思考
为什么要将区间拆分成[begin,mid] [mid + 1,end] ?
上面介绍过我们的算法步骤是把长度为 n 的输入序列分成两个长度近似为 n/2 的子序列,在此前提下,除了分成[begin,mid] [mid + 1,end]外,还有一种分法:[begin,mid-1] [mid,end],为什么不用这种分法?
mid = (begin + end)/2,所以mid是偶数
示例:用两种不同的分法分解区间[0,9]
当所要分解的区间是 [偶数,偶数],上述的两种分法都行得通,但是当区间是[偶数,偶数+1]的情况,[begin,mid-1] [mid,end]这种分法就行不通。
5.参考代码
void _MergeSort(int* arr, int* tmp, int begin, int end)
{if (begin >= end)return;int mid = (begin + end) / 2;//偶数//[begin,mid] [mid+1,end] ——>[偶数,偶数] [偶数+1,偶数+1]_MergeSort(arr,tmp, begin, mid);_MergeSort(arr, tmp, mid + 1, end);//左右区间有序就可以归并了//归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[i++] = arr[begin1++];}else{tmp[i++] = arr[begin2++];}}//剩下的尾插在tmp数组while (begin1 <= end1){tmp[i++] = arr[begin1++];}while (begin2 <= end2){tmp[i++] = arr[begin2++];}//将一定长度的tmp复制到arr中memcpy(arr + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
//归并
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail!");return;}_MergeSort(arr,tmp, 0, n - 1);free(tmp);tmp = NULL;
}不同排序对一百万个随机数进行排序的效率: (毫秒)

二、非递归实现归并排序
1.算法描述
● gap表示每组归并的数据个数
● i 表示每组归并的起始位置
● 两层循环,一层循环用来归并数组中的数据,另一层扩大归并的数据个数
2.核心步骤
(1)图示
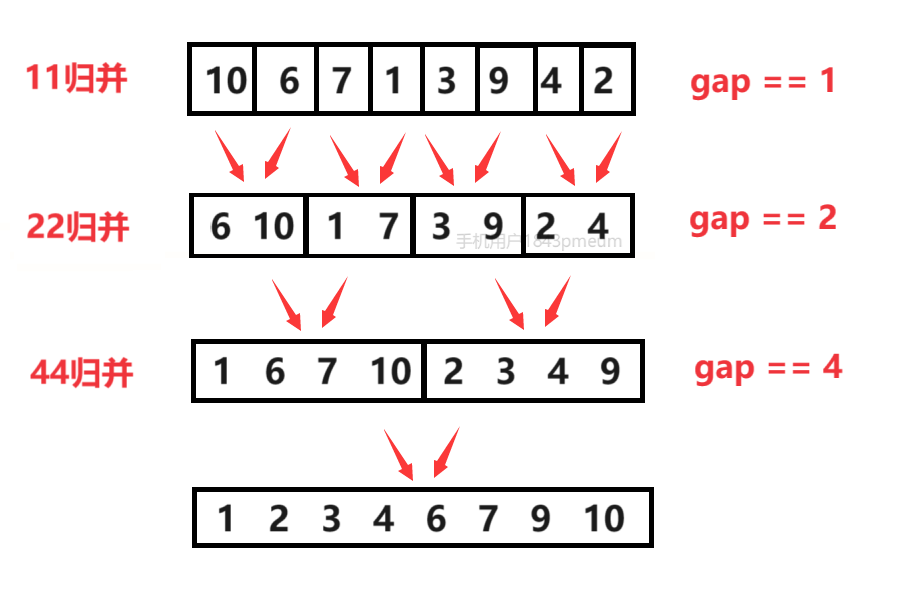

(2)思考
为什么要归并一次拷贝一次?
● 如果整体拷贝,在上述的“第二组的都越界不存在”的情况下,虽然跳出循环,但在整体拷贝的时候还会把越界的部分拷贝回去
● 但如果归并一次拷贝一次,在“第二组的都越界不存在”的情况下,直接跳出循环,不会将越界的部分拷贝到数组中
3.参考代码
//归并(非递归)
void MergeSortNonR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail!");return;}//gap表示每组要归并数据的个数int gap = 1;while (gap < n){ //i表示每组归并的起始位置for (int i = 0; i < n; i += 2 * gap)//个数于区间的转化关系{//[bagin1,end1] [bagin2,end2]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//第二组的都越界不存在,那么第二组不用归并了,跳出循环if (begin2 > n)break;//第二组的begin2没越界,end2越界了,需要修正区间,再归并if (end2 > n)end2 = n - 1;//归并int j = i;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[j++] = arr[begin1++];}else{tmp[j++] = arr[begin2++];}}//剩下的尾插在tmp数组while (begin1 <= end1){tmp[j++] = arr[begin1++];}while (begin2 <= end2){tmp[j++] = arr[begin2++];}//将一定长度的tmp复制到arr中//归并一次拷贝一次memcpy(arr + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap *= 2;}free(tmp);tmp = NULL;
}三、算法分析
归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是,代价是需要额外的内存空间。
特性总结:
(1) 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在此版中的外排序问题
(2) 时间复杂度:O(N*logN) 相当于一个满二叉树
(3) 空间复杂度:O(N) 开辟了一个额外的数组
(4) 稳定性:稳定
相关文章:
归并排序详解(递归与非递归)
归并排序是建立在归并操作上的一种有效算法。该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列间断有序。若将两个有序表合并成一个有序表,成为二路归并。 一…...
计算机系统基础(二)
1.数值数据的表示 为什么采用二进制? 二进制只有两种基本状态,两个物理器件就可以表示0和1二进制的编码、技术、运算规则都很简单0和1与逻辑命题的真假对应,方便通过逻辑门电路实现算术运算 数值数据表示的三要素 进位记数制(十…...
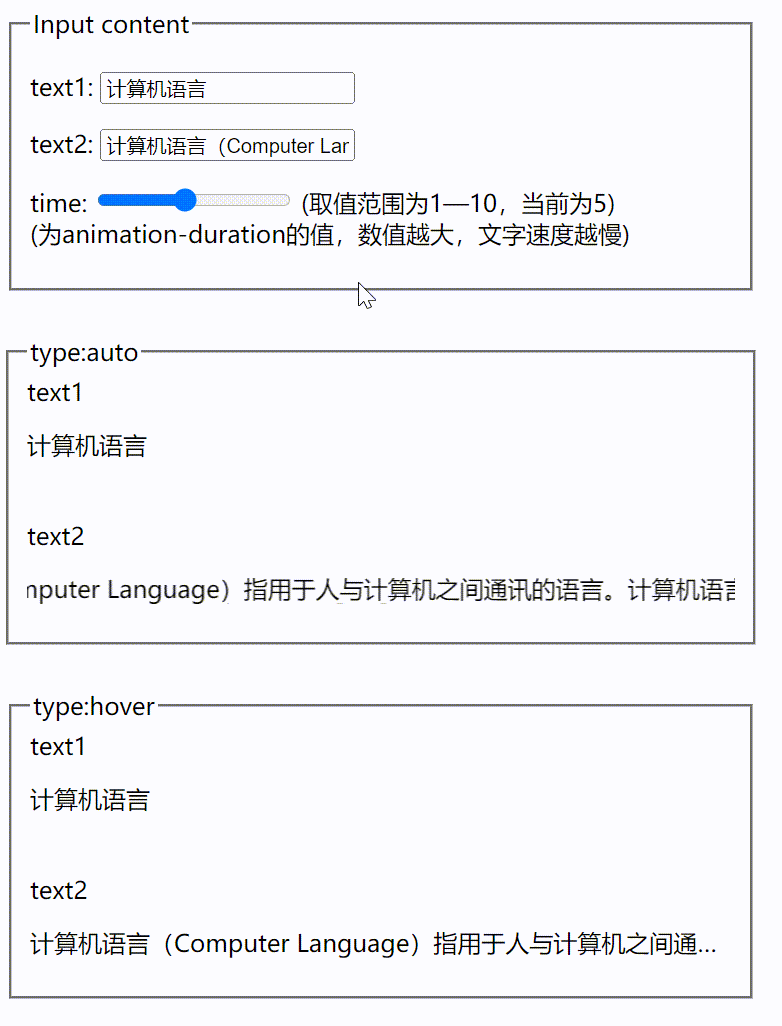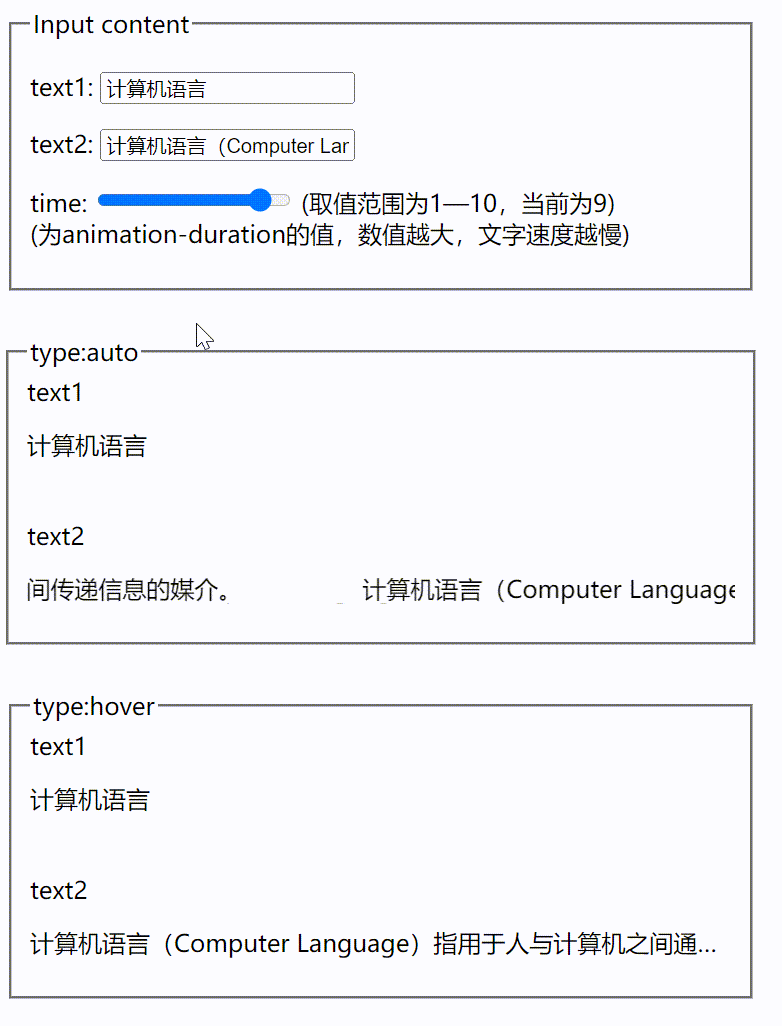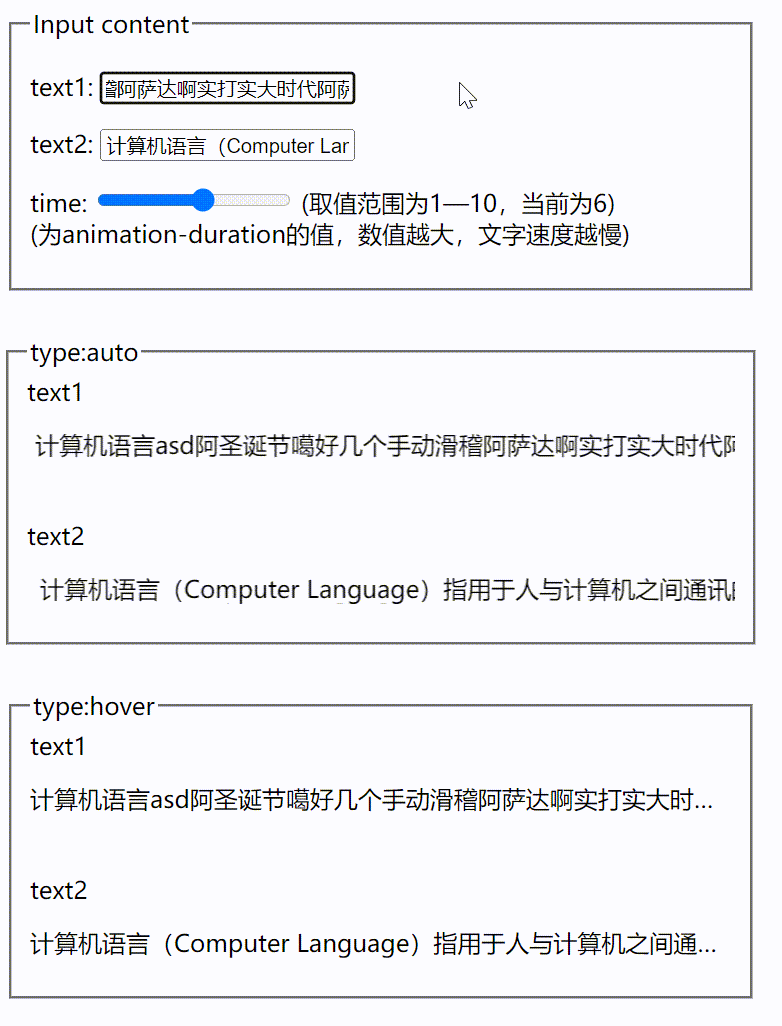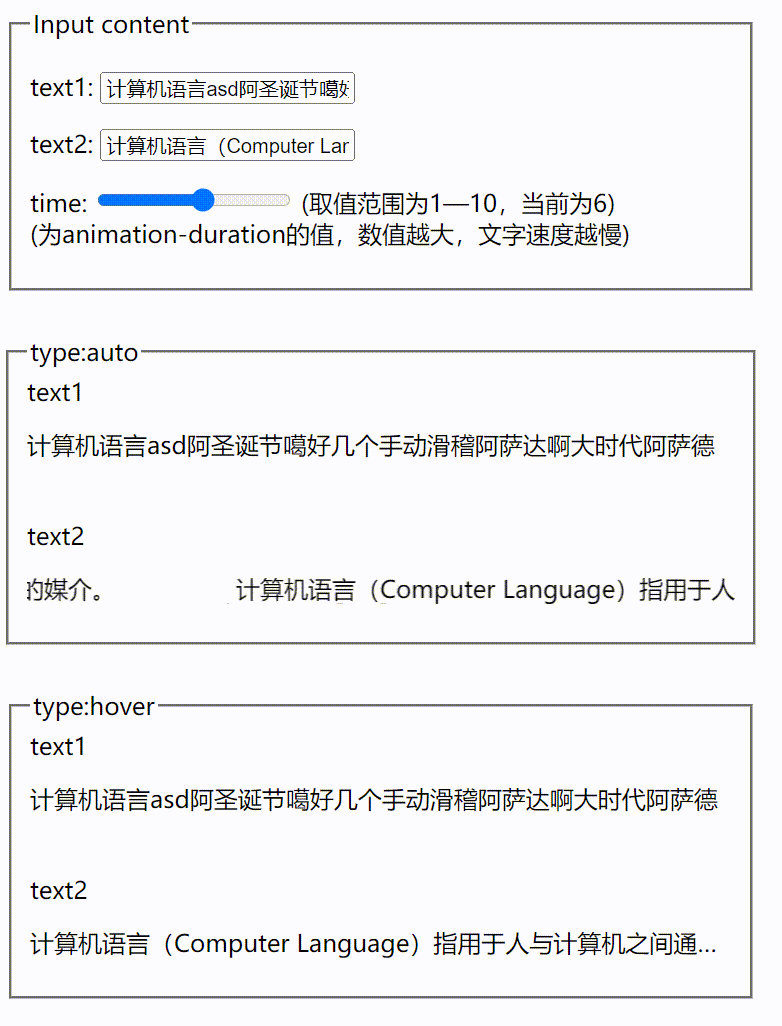
vue根据文字长短展示跑马灯效果
介绍 为大家介绍一个我编写的vue组件 auto-marquee ,他可以根据要展示文本是否超出展示区域,来判断是否使用跑马灯效果,效果图如下所示 假设要展示区域的宽度为500px,当要展示文本的长度小于500px时,只会展示文本&…...
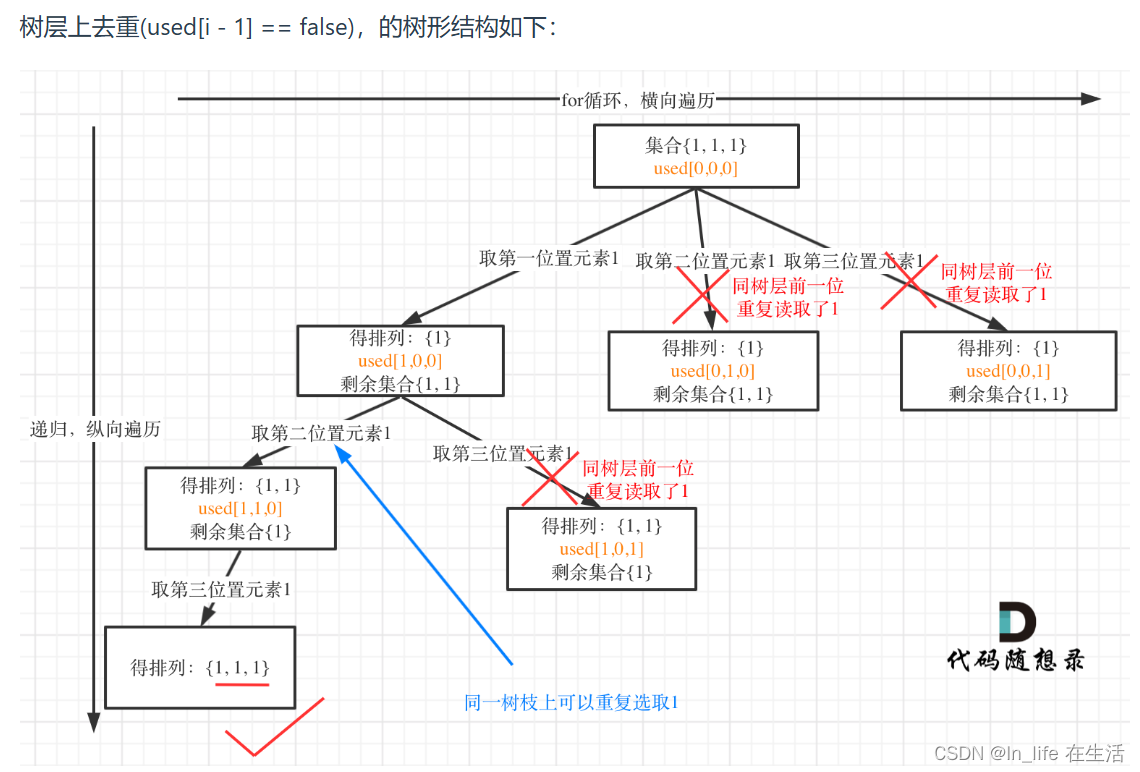
leetcode-21-回溯-全排列及其去重
一、[46]全排列 给定一个 没有重复 数字的序列,返回其所有可能的全排列。 示例: 输入: [1,2,3]输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] 其中,不需要使用startIndex used数组,其实就是记录此时path里都有哪些元素…...

如何根据两个关键字查询报错日志的位置
1、查找两个关键字(无顺序要求) 如果你不关心这两个关键字出现的顺序,你可以使用egrep(等同于grep -E)或grep的-E选项来启用扩展正则表达式,并使用管道(|)来组合两个搜索模式。 gr…...

短视频预算表:成都柏煜文化传媒有限公司
短视频预算表:精打细算,打造高质量视觉盛宴 在数字时代,短视频以其独特的魅力迅速占领了互联网内容的半壁江山,成为品牌宣传、文化传播乃至个人表达的重要载体。然而,每一个成功的短视频背后,都离不开一份…...

【Llama 2的使用方法】
Llama 2是Meta AI(Facebook的母公司Meta的AI部门)开发并开源的大型语言模型系列之一。Llama 2是在其前身Llama模型的基础上进行改进和扩展的,旨在提供更强大的自然语言处理能力和更广泛的应用场景。 以下是Llama 2的一些关键特性和更新点&am…...
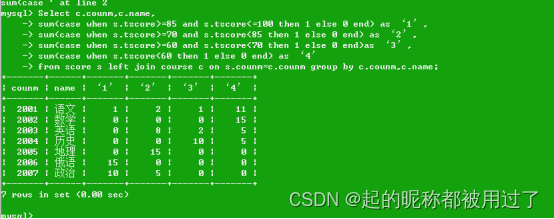
mysql-sql-第十三周
学习目标: sql 学习内容: 37.查询各科成绩最高分、最低分和平均分: 以如下形式显示:课程 ID,课程 name,最高分,最低分,平均分,及格率,中等率,优良率,优秀率 及格为>60,中等为:70-80,优良为:80-90,优秀…...

【Android】ViewPage2嵌套Fragment+SeekBar横向滑动冲突
问题描述 ViewPage2嵌套FragmentSeekBar,拖动SeekBar的进度条时,触发ViewPage2的滑动。 解决方案: 方案一:通过事件总线ViewPage2的isUserInputEnabled属性 子Fragment: class SeekBarFragment : Fragment() {priv…...

【408考点之数据结构】图的遍历
图的遍历 图的遍历是指从图中的某个顶点出发,按照一定的规则访问图中所有顶点,并使每个顶点仅被访问一次。图的遍历包括两种主要方法:深度优先搜索(DFS)和广度优先搜索(BFS)。这两种遍历方法在…...
自动驾驶---Motion Planning之多段五次多项式
1 前言 在之前的博客系列文章中和读者朋友们聊过Apollo的 Motion Planning方案: 《自动驾驶---Motion Planning之LaneChange》 《自动驾驶---Motion Planning之Path Boundary》 《自动驾驶---Motion Planning之Speed Boundary》 《自动驾驶---Motion Planning之轨迹Path优化》…...
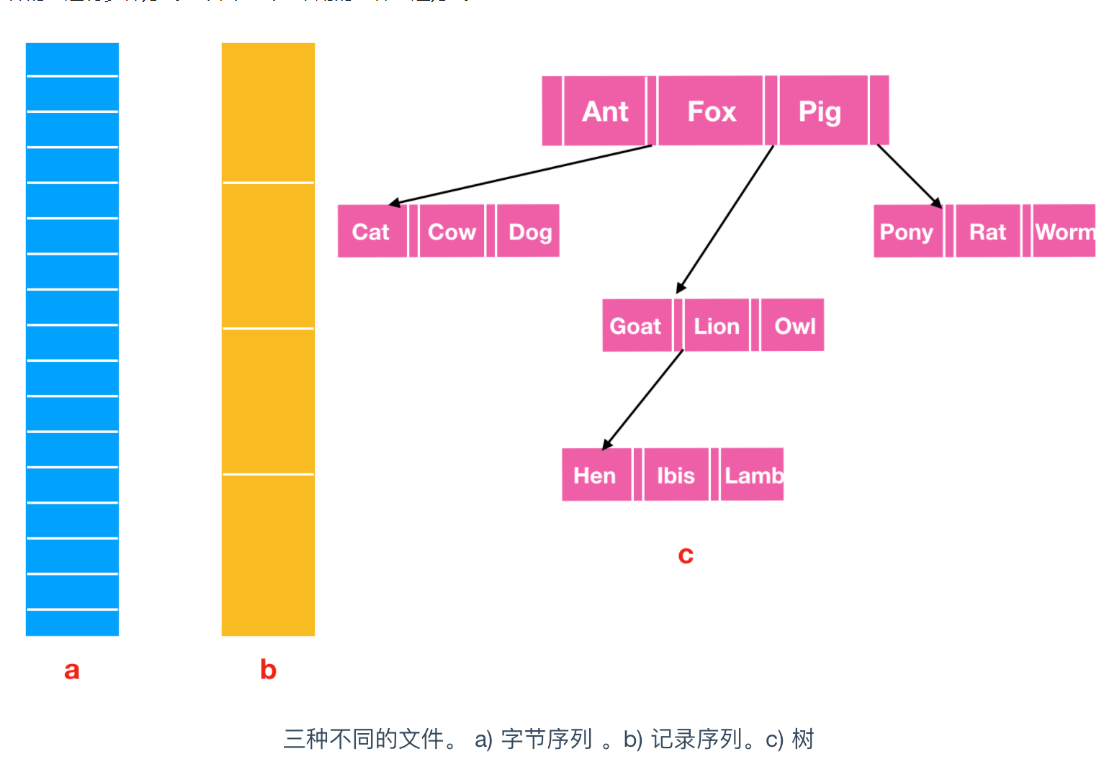
Linux基础IO操作详解
C文件IO相关接口 fopen函数 pathname: 要打开的文件名字符串mode: 访问文件的模式 模式描述含义“r”读文件不存在失败返回null“r”读写文件不存在打开失败返回null,文件存在则从头开始覆盖现有的数据(不会清空数据)“w”写文件不存在创建…...
轻松掌握:Hubstudio指纹浏览器如何接入IPXProxy代理IP
代理IP对于保护个人和企业网络安全起到了至关重要的作用,然而在需要多个工作的时候,就需要搭配指纹浏览器来使用。其中Hubstudio指纹浏览器就可以模拟多个浏览器环境,然而有些用户不知道如何将Hubstudio和代理IP一起使用,下面以…...
React小记(五)_Hooks入门到进阶
React 16.8 版本 类组件 和 函数组件 两种组件共存,到目前 React 18 版本,官方已经不在推荐使用类组件,在函数组件中 hooks 是必不可少的,它允许我们函数组件像类组件一样可以使用组件的状态,并模拟组件的生命周期等一…...

使用工业自动化的功能块实现大语言模型应用
大语言模型无所不能? 以chatGPT为代表的大语言模型横空出世,在世界范围内掀起了一场AI革命。给人的感觉似乎大模型语言无所不能。它不仅能够生成文章,图片和视频,能够翻译文章,分析科学和医疗数据,甚至可以…...
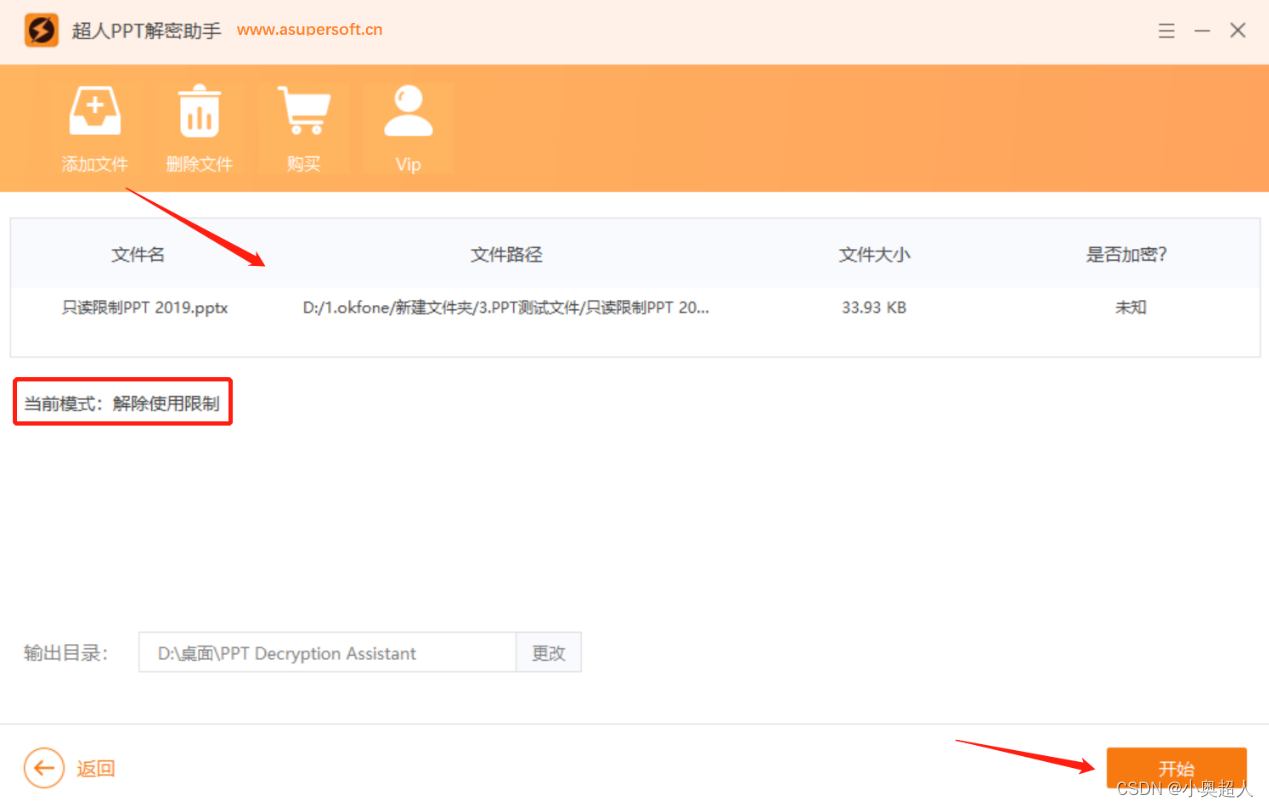
PPT文件中,母版视图与修改权限的区别
在PPT(PowerPoint)制作过程中,母版视图和修改权限是两个重要的概念,它们各自在演示文稿的编辑、管理和分发中扮演着不同的角色。本文将从定义、功能、使用场景及区别等方面详细探讨PPT母版视图与修改权限的异同。 PPT母版视图 定…...

php简单的单例模式
本文由 ChatMoney团队出品 单例模式是一种常用的设计模式,它的核心思想是确保一个类只有一个实例,并提供一个全局访问点来获取这个实例。在 PHP 中实现单例模式通常有三种形式:饿汉式(Eager)、懒汉式(Lazy&…...
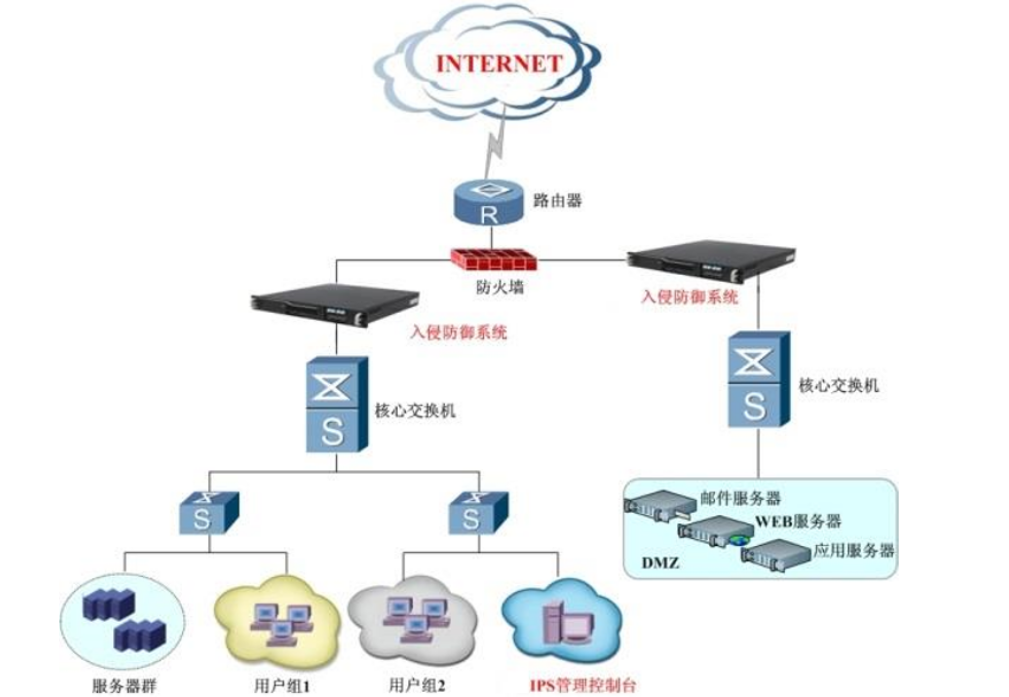
【面试题】IPS(入侵防御系统)和IDS(入侵检测系统)的区别
IPS(入侵防御系统)和IDS(入侵检测系统)在网络安全领域扮演着不同的角色,它们之间的主要区别可以归纳如下: 功能差异: IPS:这是一种主动防护设备,不仅具备检测攻击的能力&…...

宠物博主亲测养宠好物安利,口碑好的狗毛空气净化器推荐
作为一名6年资深铲屎官,一到春季换季就开始各种疯狂打喷嚏、全身过敏红肿,这是因为宠物在换季的时候就疯狂掉毛,家里就想下雪一样,空气中都是宠物浮毛。而宠物毛上附带的细菌会跟随浮毛被人吸入人体,从而产生打喷嚏、过…...

常用工具类
计算当天开始时间和结束时间 DateTime date DateUtil.date(); String startDateStr DateUtil.formatDateTime(DateUtil.beginOfDay(date)); String endDateStr DateUtil.formatDateTime(DateUtil.beginOfDay(DateUtil.offsetDay(date,1))); params.put("startDate&quo…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...

VASP软件在第一性原理计算中的应用-测试GO
VASP软件在第一性原理计算中的应用 VASP是由维也纳大学Hafner小组开发的一款功能强大的第一性原理计算软件,广泛应用于材料科学、凝聚态物理、化学和纳米技术等领域。 VASP的核心功能与应用 1. 电子结构计算 VASP最突出的功能是进行高精度的电子结构计算ÿ…...