atcoder ABC 357-D题详解
atcoder ABC 357-D题详解
Problem Statement
For a positive integer N, let VN be the integer formed by concatenating N exactly N times.
More precisely, consider N as a string, concatenate N copies of it, and treat the result as an integer to get VN.
For example, V3=333 and V10=10101010101010101010.
Find the remainder when VN is divided by 998244353.
Constraints
1≤N≤1018
N is an integer.
Input
The input is given from Standard Input in the following format:
N
Output
Print the remainder when VN is divided by 998244353.
Sample Input 1
5
Sample Output 1
55555
The remainder when V5=55555 is divided by 998244353 is 55555.
Sample Input 2
9
Sample Output 2
1755646
The remainder when V9=999999999 is divided by 998244353 is 1755646.
Sample Input 3
10000000000
Sample Output 3
468086693
Note that the input may not fit into a 32-bit integer type.
思路分析1:
暴力直接写,re和tle
code:
#include <iostream>
#include <string>
#include <vector>
using namespace std;
typedef long long ll;
string s;
vector<string>v;
ll n;
int main(){cin>>s;//s本来就有一个,所以后面要减1ll n=stoll(s);for(ll i=0;i<n-1;i++){v.push_back(s);}for(ll i=0;i<n-1;i++){s=s+v[i];}ll cnt=stoll(s);cnt=cnt%998244353;cout<<cnt;
}
思路分析2:
本题使用快速幂,先拼接,可以发现是等比数列,然后使用等比数列求和公式,因为数太大会爆ll,所以使用欧拉定理和费马小定理分别化简式子来优化时间复杂度,最后答案也要先mod后乘,不然会爆ll。
code:
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
const int mod=998244353;
ll n;
int qpow(int a,int n){//不用欧拉定理应该为ll nint res=1;while(n){if(n&1) res=1ll*res*a%mod;a=1ll*a*a%mod;n>>=1;}return res;
}
int getlen(ll n){int ans=0;while(n){ans++;n/=10;}return ans;
}
int main(){cin>>n;int l=getlen(n);int c1=qpow(10,n%(mod-1)*l%(mod-1))-1;//n*l会爆ll所以要分别先mod//不用欧拉定理c1=qpow(10,qpow(10,l),n)-1;int c2=qpow(10,l)-1;c2=qpow(c2,mod-2);int ans=1ll*n%mod*c1%mod*c2%mod;cout<<ans;return 0;
}
相关文章:

atcoder ABC 357-D题详解
atcoder ABC 357-D题详解 Problem Statement For a positive integer N, let VN be the integer formed by concatenating N exactly N times. More precisely, consider N as a string, concatenate N copies of it, and treat the result as an integer to get VN. For…...
从单一到多元:EasyCVR流媒体视频汇聚技术推动安防监控智能升级
随着科技的飞速发展,视频已成为我们日常生活和工作中的重要组成部分。尤其在远程办公、在线教育、虚拟会议等领域,视频的应用愈发广泛。为了满足日益增长的视频需求,流媒体视频汇聚融合技术应运而生,它不仅改变了传统视频的观看和…...
JSON数据的回写)
Spring MVC数据绑定和响应——数据回写(二)JSON数据的回写
项目中已经导入了Jackson依赖,可以先调用Jackson的JSON转换的相关方法,将对象或集合转换成JSON数据,然后通过HttpServletResponse将JSON数据写入到输出流中完成回写,具体步骤如下。 1、修改文件DataController.java,在…...
怎么快速给他人分享图片?扫描二维码看图的简单做法
现在通过二维码来查看图片是一种很常见的方法,通过二维码来查看图片不仅能够减少对手机存储空间的占用,而且获取图片变得更加方便快捷,只需要扫码就能够查看图片,有利于图片的展现。很多的场景中都有图片二维码的应用,…...
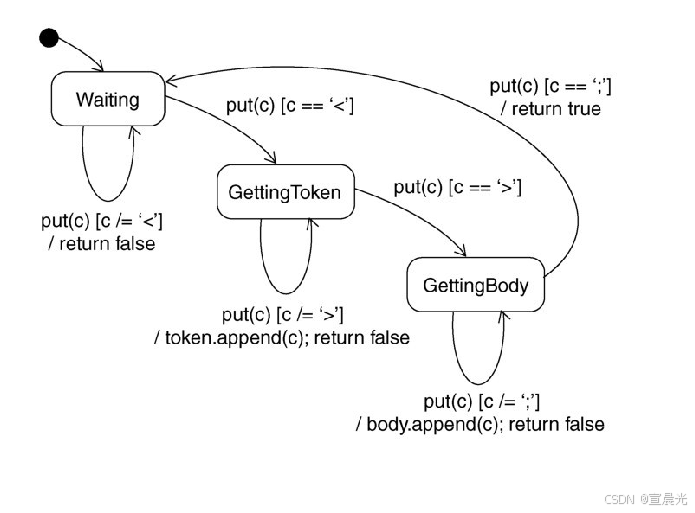
【UML用户指南】-26-对高级行为建模-状态图
目录 1、概念 2、组成结构 3、一般用法 4、常用建模技术 4.1、对反应型对象建模 一个状态图显示了一个状态机。在为对象的生命期建模中 活动图展示的是跨过不同的对象从活动到活动的控制流 状态图展示的是单个对象内从状态到状态的控制流。 在UML中,用状态图…...
解决VSCode无法用ssh连接远程服务器的问题
原因: 因为windows自带的ssh无法连接远程服务器,需要用git底下的ssh.exe。 搜了很久,试过很多方法,包括替换掉环境变量中的ssh,但是都无效,最后发现是要在VSCode中配置需要使用哪个ssh.exe。 步骤&#…...
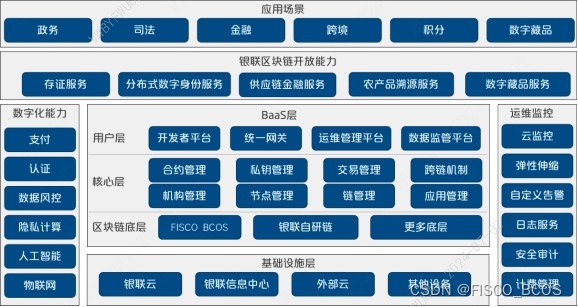
【区块链+基础设施】银联云区块链服务 | FISCO BCOS应用案例
为了顺应区块链基础设施化的发展趋势,中国银联推出了银联云区块链服务——UPBaaS,为金融行业采用区块链 技术提出了解决方案,微众银行为平台提供 FISCO BCOS 区块链开源技术支持。通过银联云区块链服务,用户可 以用可视化的方式创…...
 死锁 死锁发生条件)
Java SE入门及基础(61) 死锁 死锁发生条件
目录 死锁 1. 死锁的概念 2. 死锁发生条件 互斥条件 不可剥夺条件 请求与保持条件 循环等待 3. 案例分析 示例 分析 死锁 1. 死锁的概念 Deadlock describes a situation where two or more threads are blocked forever, waiting for each other 死锁描述了一种情…...
简单爬虫案例——爬取快手视频
网址:aHR0cHM6Ly93d3cua3VhaXNob3UuY29tL3NlYXJjaC92aWRlbz9zZWFyY2hLZXk9JUU2JThCJTg5JUU5JTlEJUEy 找到视频接口: 视频链接在photourl中 完整代码: import requestsimport re url https://www.kuaishou.com/graphql cookies {did: web_…...

42、nginx之nginx.conf
nginx----web服务器 一、nginx http就是apache,在国内很少。 nginx是开源的,是一款高性能,轻量级的web服务软件。 稳定性高,而且版本迭代比较快(修复bug速度比较快,安全性快) 消耗系统资源…...

高薪程序员必修课-java为什么要用并发编程
目录 前言 1. 提高性能和效率 2. 更好地响应用户 3. 优化I/O操作 具体示例 示例1:提高性能和效率 示例2:更好地响应用户 示例3:优化I/O操作 总结 前言 并发编程允许多个线程在同一时间执行任务。下面我们从多个原理角度来解释为什么J…...

postgreSQL学习
postgreSql学习 学习参考:1、命令1.1 登录1.2 关闭连接 2、常用数据类型2.1 数值类型2.2 字符串类型2.3 时间2.4 其他 3、自增主键4、sql4.1 库操作(1)创建新库(2)切换数据库(3)删库【谨慎&…...
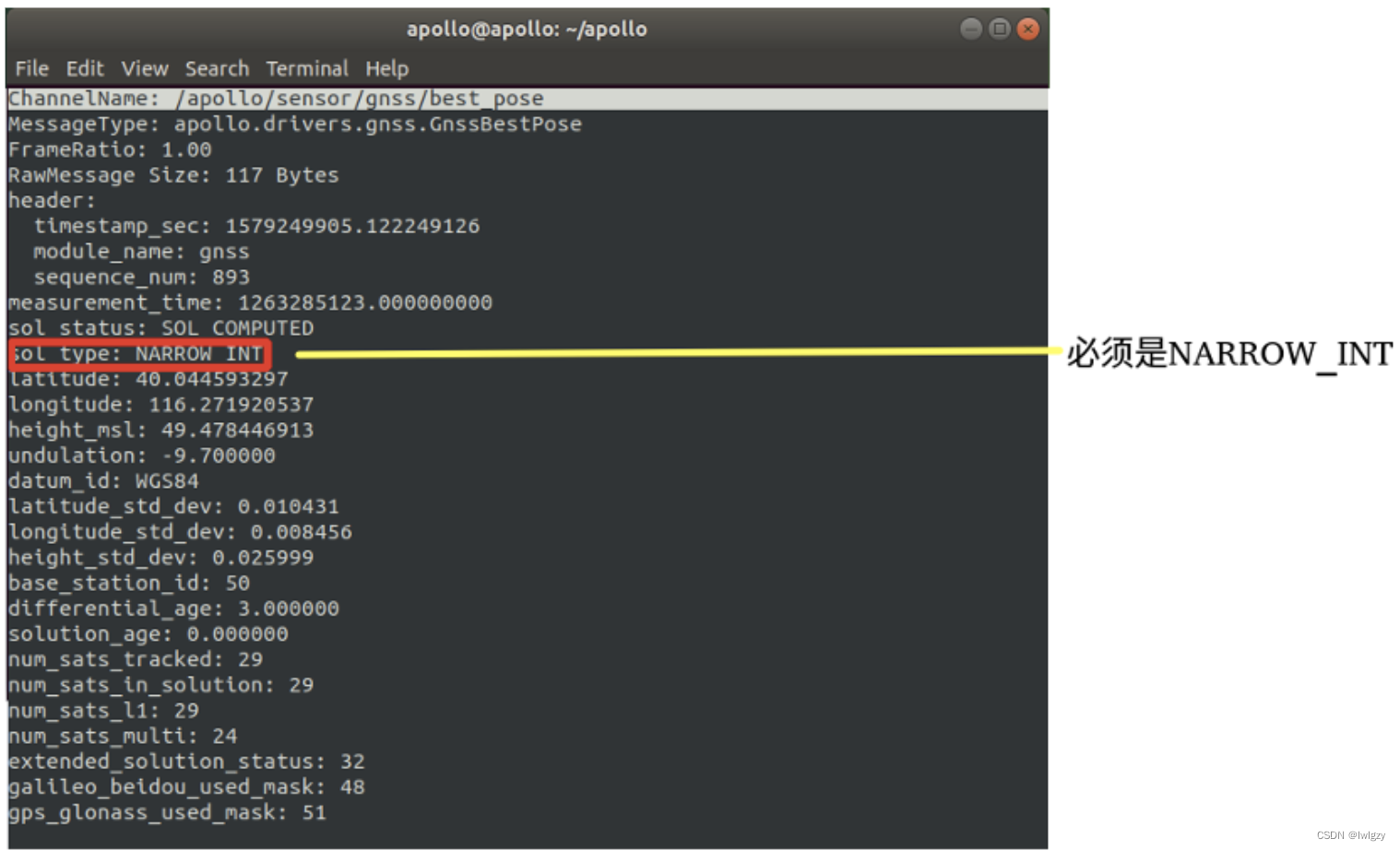
【3】系统标定
文章目录 雷达标定相机主雷达标定底盘动力学标定车辆循迹验证建图 雷达标定 主要是为了获得到lidar到imu的tf关系。imu为父坐标lidar为子坐标。其他雷达标定到主lidar坐标系下。 标定的结果都是生成一个是四元数。 #mermaid-svg-crOWRnT4UE0jtJVy {font-family:"trebuch…...

网安小贴士(3)网安协议
一、前言 网络安全协议是构建安全网络环境的基础,它们帮助保护网络通信免受各种威胁和攻击。 二、定义 网络安全协议是指在计算机网络中用于确保网络通信和数据传输安全的协议。它们定义了在网络通信过程中的安全机制、加密算法、认证和授权流程等,以保…...
)
大数据面试题之HBase(1)
目录 介绍下HBase HBase优缺点 说下HBase原理 介绍下HBase架构 HBase读写数据流程 HBase的读写缓存 在删除HBase中的一个数据的时候,它什么时候真正的进行删除呢?当你进行删除操作,它是立马就把数据删除掉了吗? HBase中的二级索引 HBa…...

git回退commit的方式
在Git中,回退commit(即撤销之前的提交)可以通过多种方式来实现。以下是一些常见的方法,以及它们的详细步骤和注意事项: ### 1. 使用git revert命令 git revert命令用于撤销某次commit,但它并不会删除该comm…...
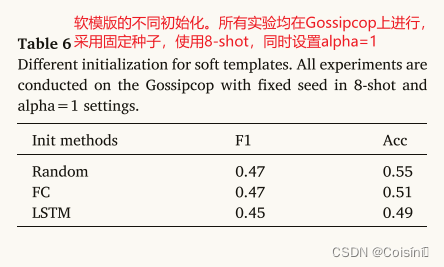
[Information Sciences 2023]用于假新闻检测的相似性感知多模态提示学习
推荐的一个视频:p-tuning P-tunning直接使用连续空间搜索 做法就是直接将在自然语言中存在的词直接替换成可以直接训练的输入向量。本身的Pretrained LLMs 可以Fine-Tuning也可以不做。 这篇论文也解释了为什么很少在其他领域结合知识图谱的原因:就是因…...

自定义vue3 hooks
文章目录 hooks目录结构demo hooks 当页面内有很多的功能,js代码太多,不好维护,可以每个功能都有写一个js或者ts,这样的话,代码易读,并且容易维护,组合式setup写法与此结合👍&#…...
《昇思25天学习打卡营第21天 | 昇思MindSporePix2Pix实现图像转换》
21天 本节学习了通过Pix2Pix实现图像转换。 Pix2Pix是基于条件生成对抗网络(cGAN)实现的一种深度学习图像转换模型。可以实现语义/标签到真实图片、灰度图到彩色图、航空图到地图、白天到黑夜、线稿图到实物图的转换。Pix2Pix是将cGAN应用于有监督的图…...
【文档+源码+调试讲解】科研经费管理系统
目 录 目 录 摘 要 ABSTRACT 1 绪论 1.1 课题背景 1.2 研究现状 1.3 研究内容 2 系统开发环境 2.1 vue技术 2.2 JAVA技术 2.3 MYSQL数据库 2.4 B/S结构 2.5 SSM框架技术 3 系统分析 3.1 可行性分析 3.1.1 技术可行性 3.1.2 操作可行性 3.1.3 经济可行性 3.1…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
