【基础算法总结】分治—快排
分治—快排
- 1.分治
- 2.颜色分类
- 3.排序数组
- 4.数组中的第K个最大元素
- 5.库存管理 III

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.分治
分治思想就如同它的名字一样:分而治之。
将一个大问题划分成若干个相同或者相识的子问题。然后在将子问题在划分成若干个相同或者相识的子问题,直到划分到不能在划分。然后解决子问题,子问题都解决完了,大问题也就被解决完了。快速排序和归并排序就用的分治思想。
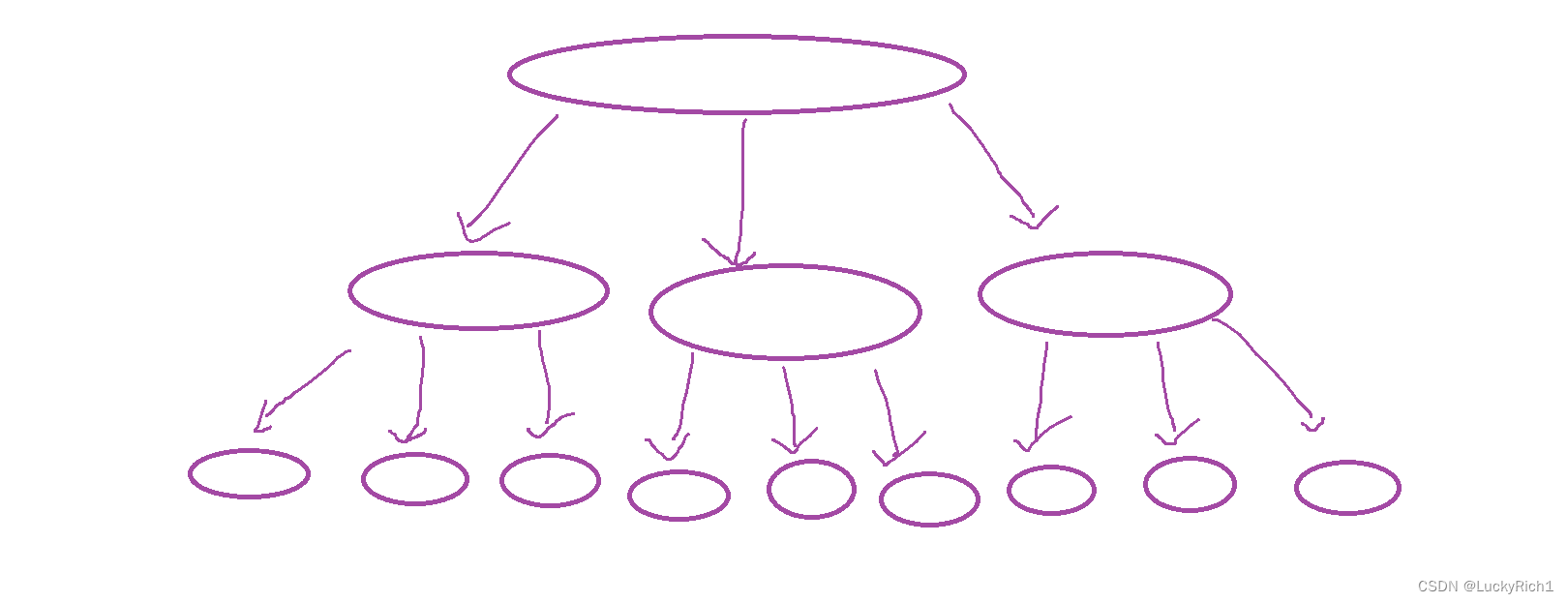
以前我们学快速排序是在数组中选择一个基准元素,然后将数组分成左右两个区间,左区间比基准元素小,右区间比基准元素大。然后递归的去左区间和有区间排序,这种做法是将数组分成了两份。但是对于重复元素非常多的数组即使使用快速排序也会超时。因此这里我们学习新的划分方法,将数组划分成三份。
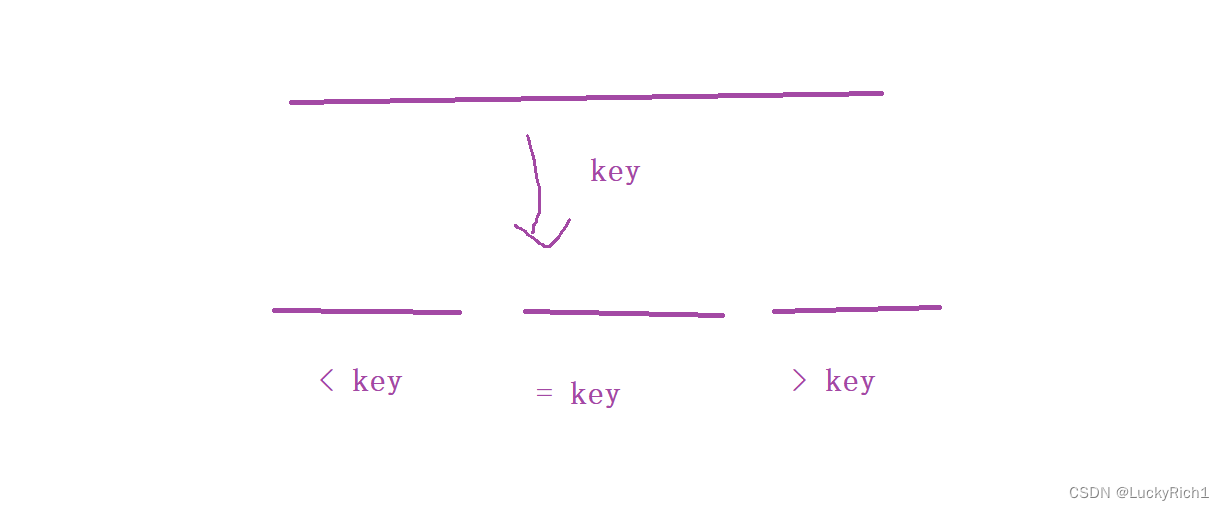
还是选一个基准元素将数组划分成三份,左区间元素都比基准元素小。中间区间元素和基准元素相同,右区间元素都比基准元素大。因为中间都是等于key的一定就是在最终位置,所以接下来递归还是只考虑左区间和右区间。
2.颜色分类
题目链接:75. 颜色分类
题目分析:

说起来这道题并不是真正的分治快速排序,而是把数组按照一定规则划分成三块的。当把这道题解决后,快排写的就非常简单。
这道题就相当于选择一个基准元素1,把小于1的放左边,大于1的放右边,等于1的放中间。
算法原理:
双指针可以将数组分成两块,具体怎么分,双指针系列第一道题移动零。这里我们需要三个指针将数组分成三块!
每个指针的作用:
i指针:遍历整个数组
left:标记 0 区域的最右侧
right:标记 2 区域的最左侧

三个指针将数组分成4份:
[0,left] :全都是0
[left+1,i-1]:全都是1
[i,right-1]:待扫描的元素
[rigth+1,n-1]:全都是2
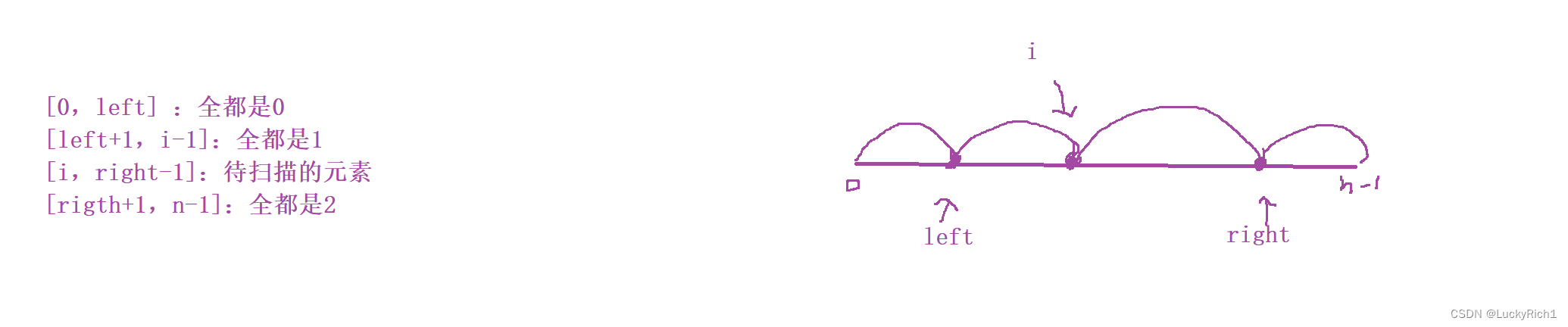
接下来就讨论nums[i]是0或1或2应该怎么办?
当nums[i]为0的时候,要把0加入到左边区域,left指向的是 0 最右侧区域,此时left+1,然后将 i 位置和 left+1 元素交换,然后i+1。
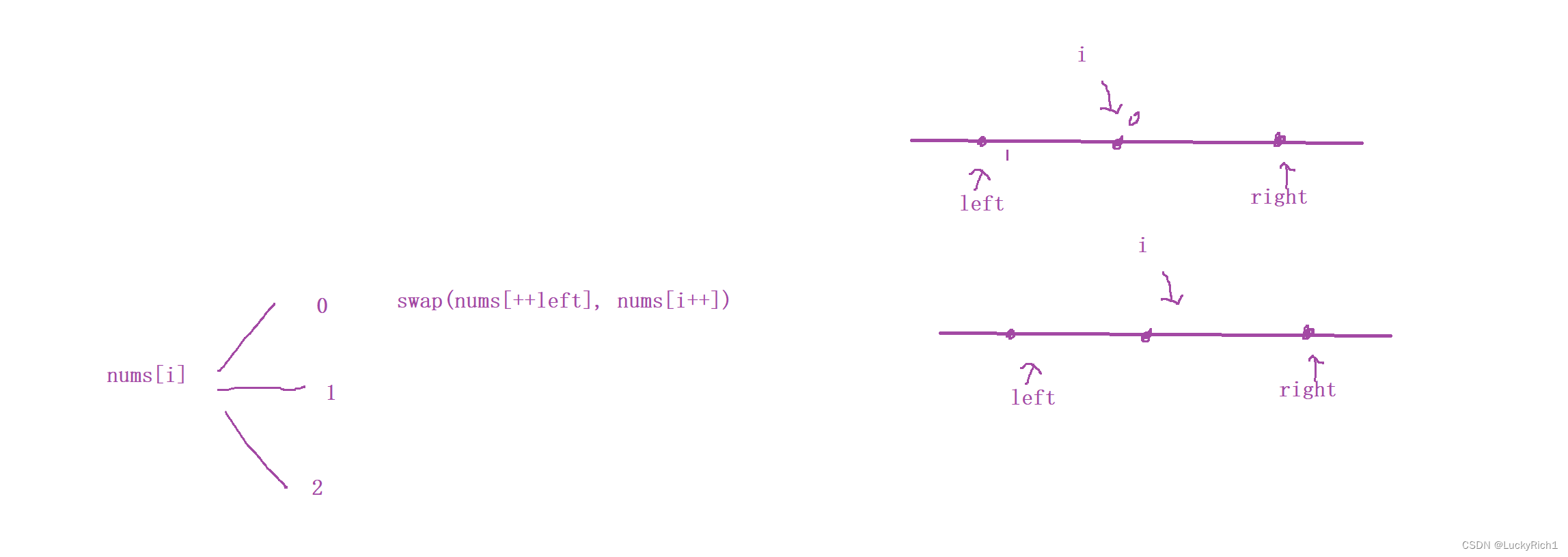
还有一种极端情况 i 就在 left+1的为位置,并且正好是0。但是这种处理方法和上面一样。
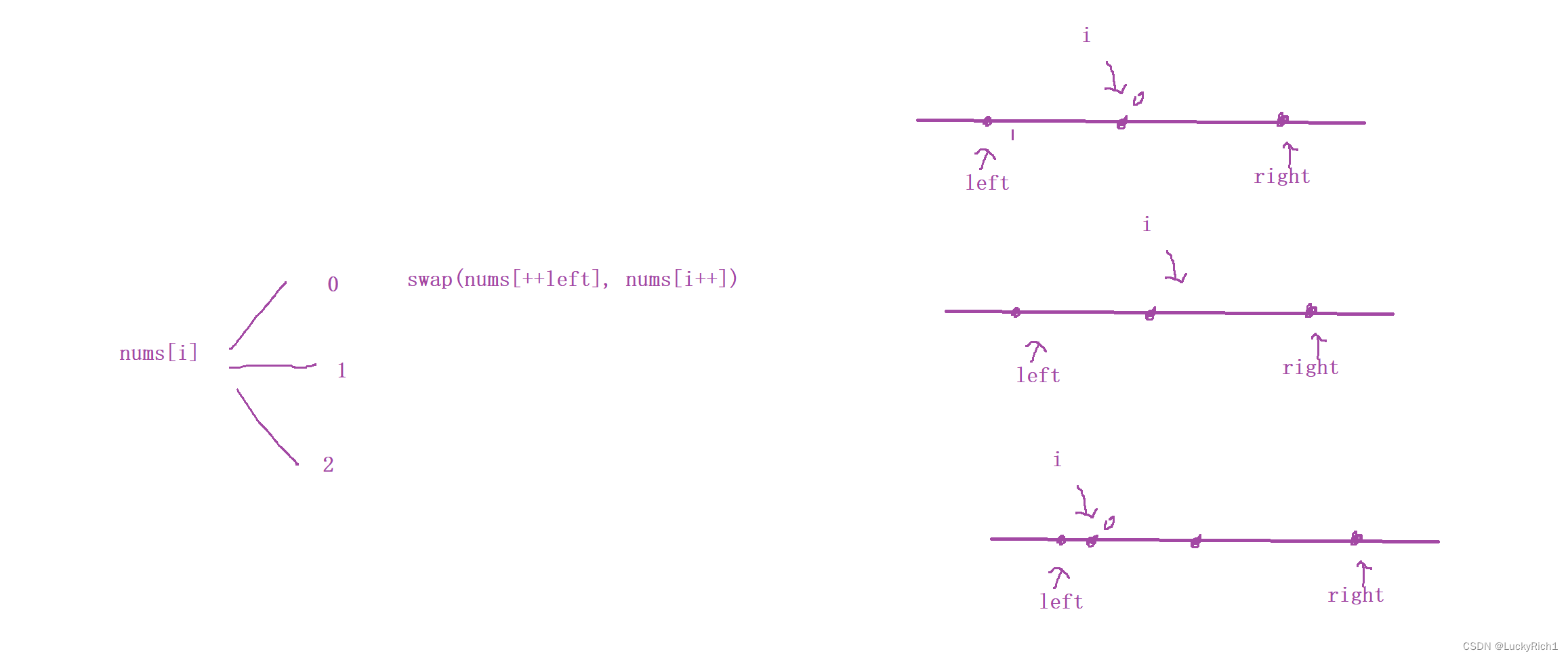
当nums[i]为1的时候,i 指针往后走就行了
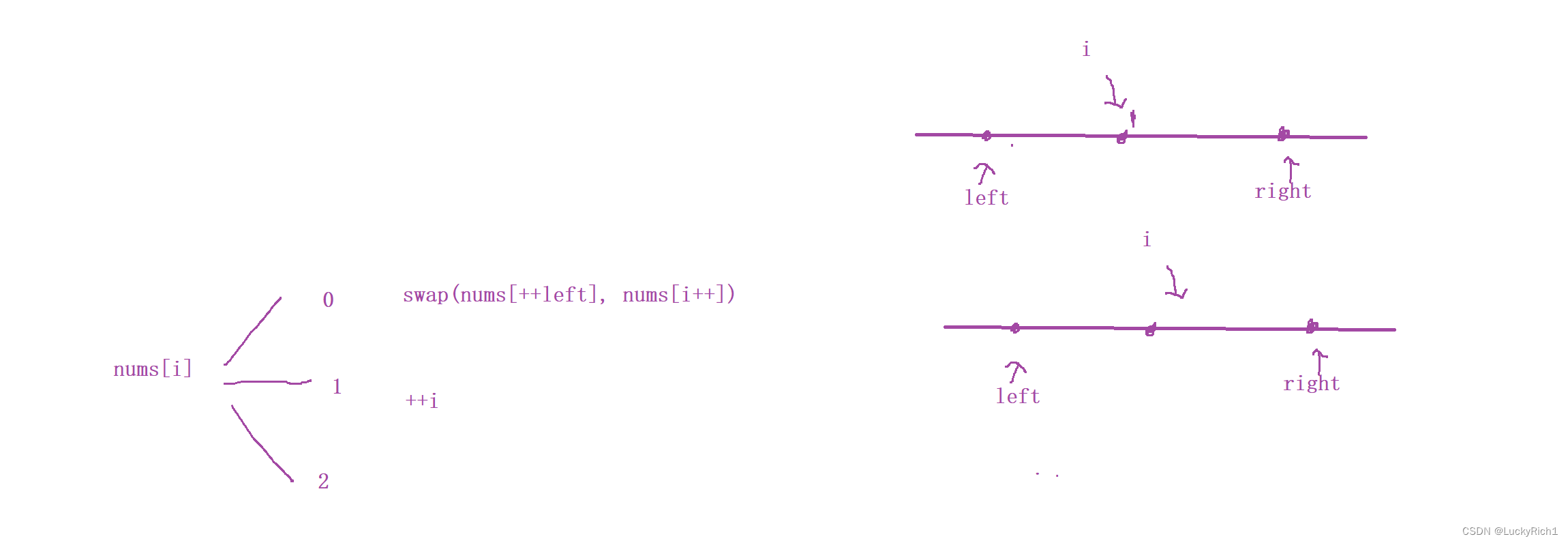
当nums[i]为2的时候,我们要将2加入到右边区间,也就是加入到 right - 1 的位置。交换 i 位置和 right -1 位置的元素。但是此时需要注意的是 交换给 i 位置的元素是待扫描的元素,因此 i 指针不能往后走!
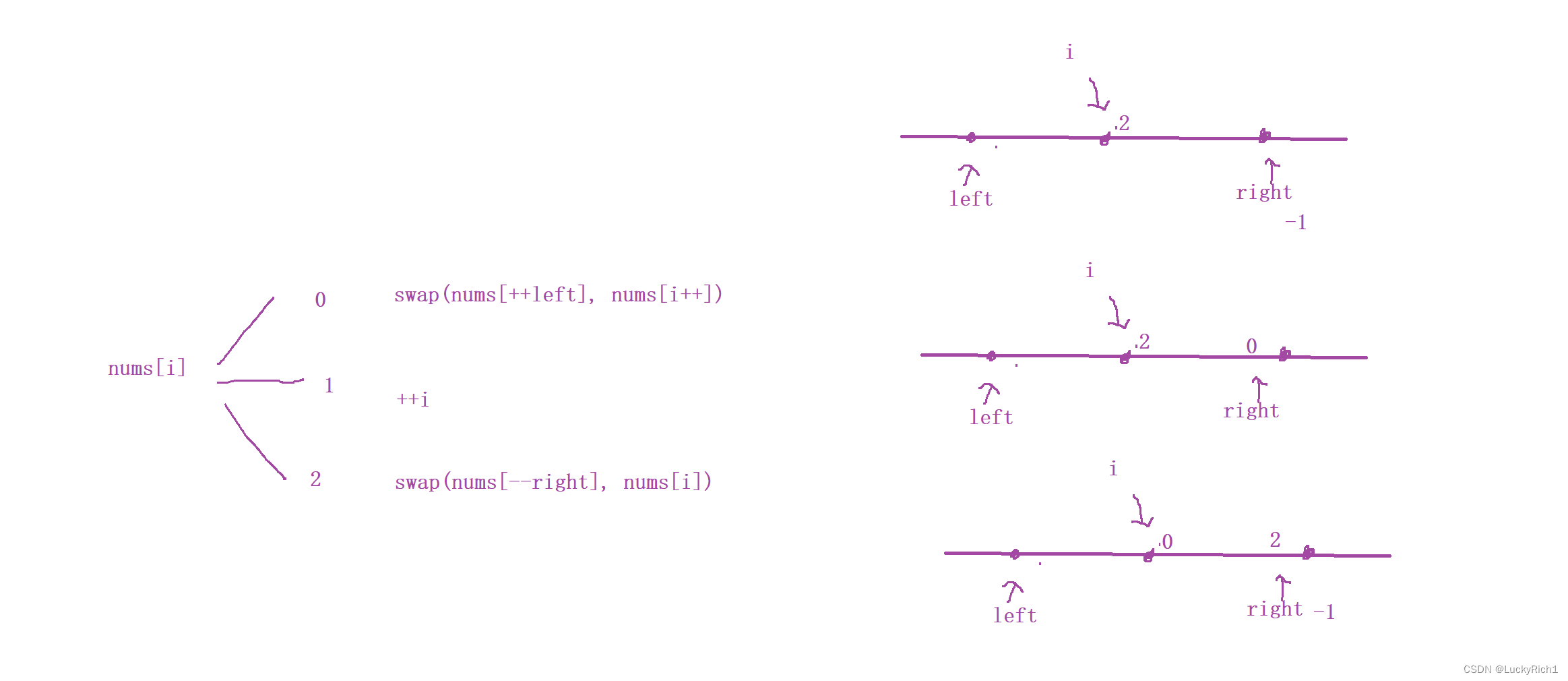
class Solution {
public:void sortColors(vector<int>& nums) {int n = nums.size();int i = 0, left = -1, right = n;while(i < right){if(nums[i] == 0)swap(nums[++left], nums[i++]);else if(nums[i] == 2)swap(nums[--right], nums[i]);else++i;}}
};
3.排序数组
题目链接:912. 排序数组
题目描述:

算法原理:
在数组中选择一个基准元素key,根据key将数组分成左右区间,左区间元素小于等于key,右区间元素大于key。这个key就处于排序的最终位置。然后在将左区间排排序,右区间排排序,重复上述过程。整体就有序了。时间复杂度(nlogn)
但是如果数组都是重复元素,此时选择基准元素间将数组分成左右两区间就不行了。时间复杂度退化成O(n^2)

所以我们学习一个更优的做法,将 数组分三块 思想来实现快速排序
我们先选一个基准元素key,将数组分成三块。左区间小于key,中间区间等于key,右区间大于key。中间区间已经在排序后的最终位置,所以只用去去左区间排序,右区间排序。重复上述过程,整体就有序了。
数组如何分三块和颜色分类一模一样。定义一个i 指针 扫描数组,left指针 指向左区间小于key的最右侧, right指针 指向右区间大于key的最左侧。然后分情况讨论就好了。

即使数组全部都是重复元素,我们经过一次数组划分,整个数组都是中间区间,左右区间不存在,也不用在递归下去了,直接结束。时间复杂度O(n)
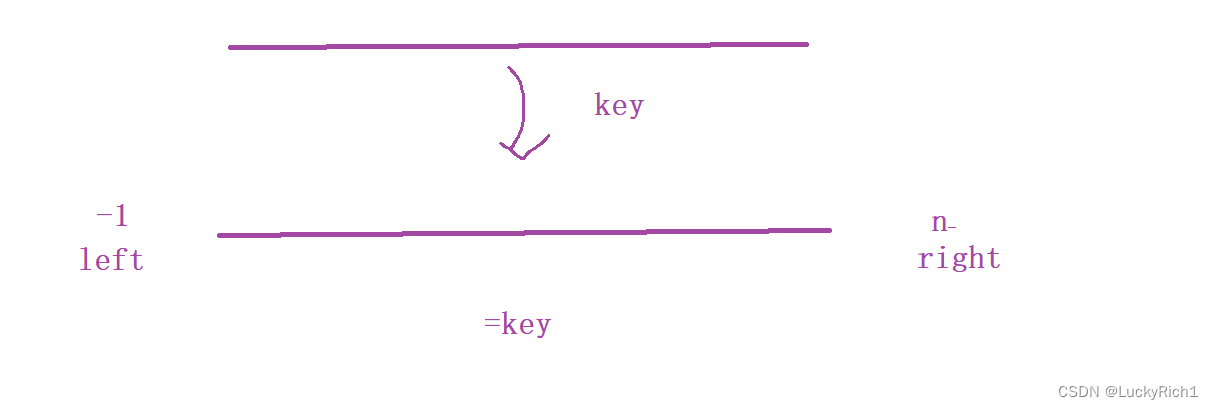
优化:用随机的方式选择基准元素
之前常用的三数取中,还是不够随机。要想时间复杂度逼近O(nlogn)就要用随机的方式选择基准元素。
随机选择就是让数组中每个元素被选择的概率相同,然后返回被选择的元素。
使用产生随机数的函数 rand(),让生成的随机数%这个区间的长度,然后加上left,这是在这个区间内的随机数的下标,然后返回对应下标的元素。

class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand((unsigned int)time(nullptr));QuickSort(nums,0,nums.size()-1);return nums;}void QuickSort(vector<int>& nums, int l, int r){if(l >= r) return;//数组分三块int key = getRandom(nums, l ,r);int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] < key)swap(nums[++left], nums[i++]);else if(nums[i] == key)++i;elseswap(nums[--right], nums[i]);}QuickSort(nums, l , left);QuickSort(nums, right, r);}int getRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}
4.数组中的第K个最大元素
题目链接:215. 数组中的第K个最大元素
题目分析:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。其实就是一个TopK问题。
TopK问题四种问法:
第 k 个最大的元素
第 k 个最小的元素
前 k 个最大的元素
前 k 个最小的元素
可以使用堆排序, 时间复杂度O(nlogn)
还有一种就是快速选择算法,快速选择算法是基于快排实现的。时间复杂度O(n)。
算法原理:
一定要把数组分三块+随机选择基准元素掌握,才能懂这道题。
核心操作还是选择一个基准元素key,将数组分成< key , = key ,> key 三块区域。在这道题中我们是要找到第K大元素,这个第K大元素有可能落在三个区域中的任何一个区域。如果有一种方法能够确定第K大元素能够落在那个区域,那另外两个区域就不用考虑了。仅需在确定的区域里面递归找。所以说它是比快排更快的一种算法。
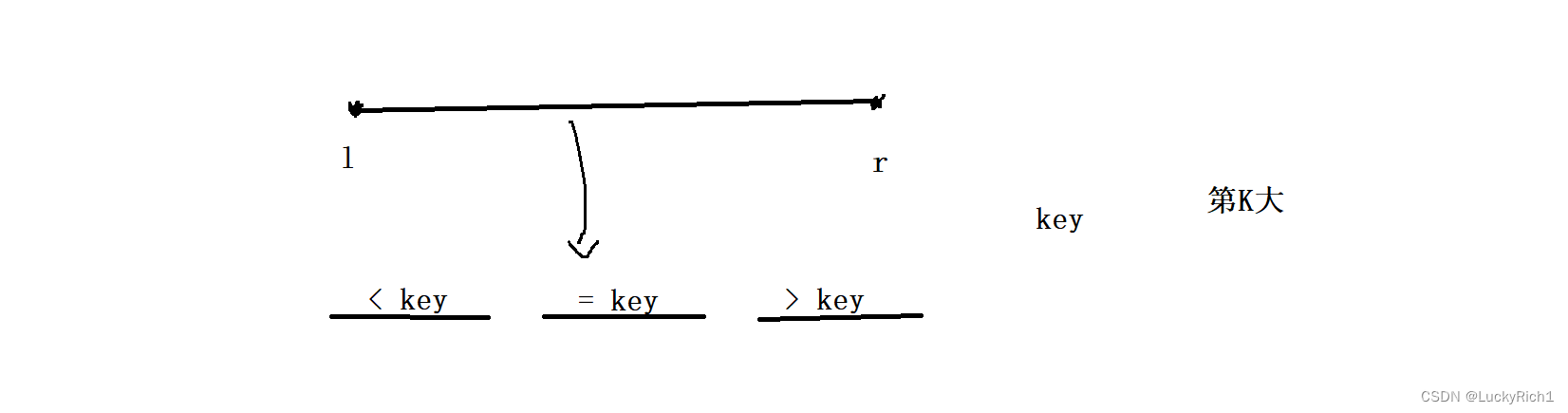
接下来重点就是如何确定第K大元素落在左边区域、中间区域、还是右边区域。
此时我们先统计出每个区域中元素的个数,假设左边区域元素个数为 a,中间区域元素个数为 b,右边区域元素个数为 c。
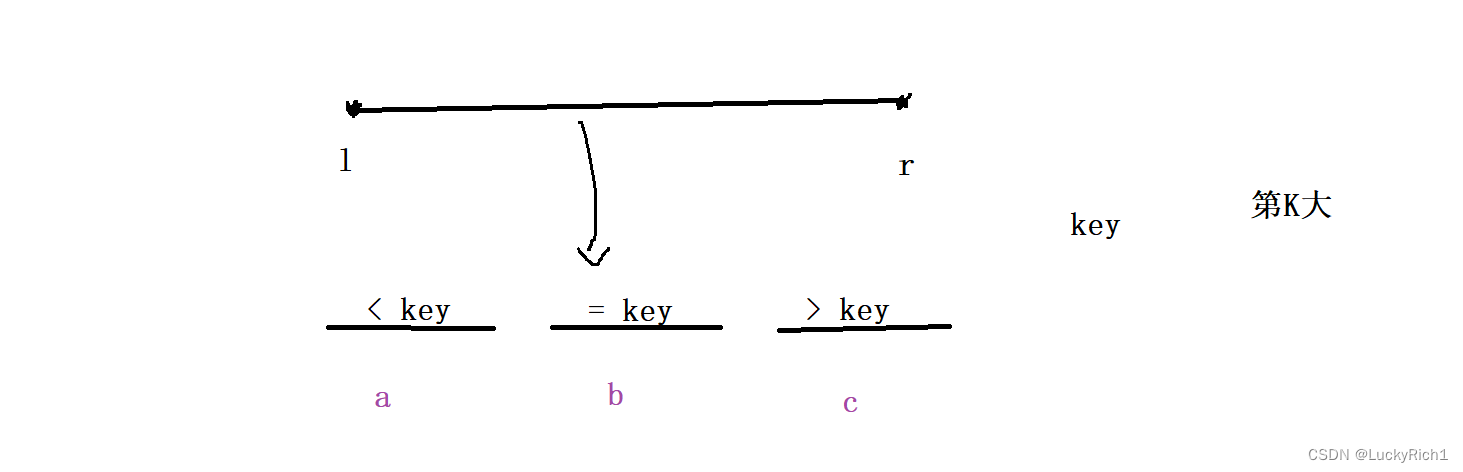
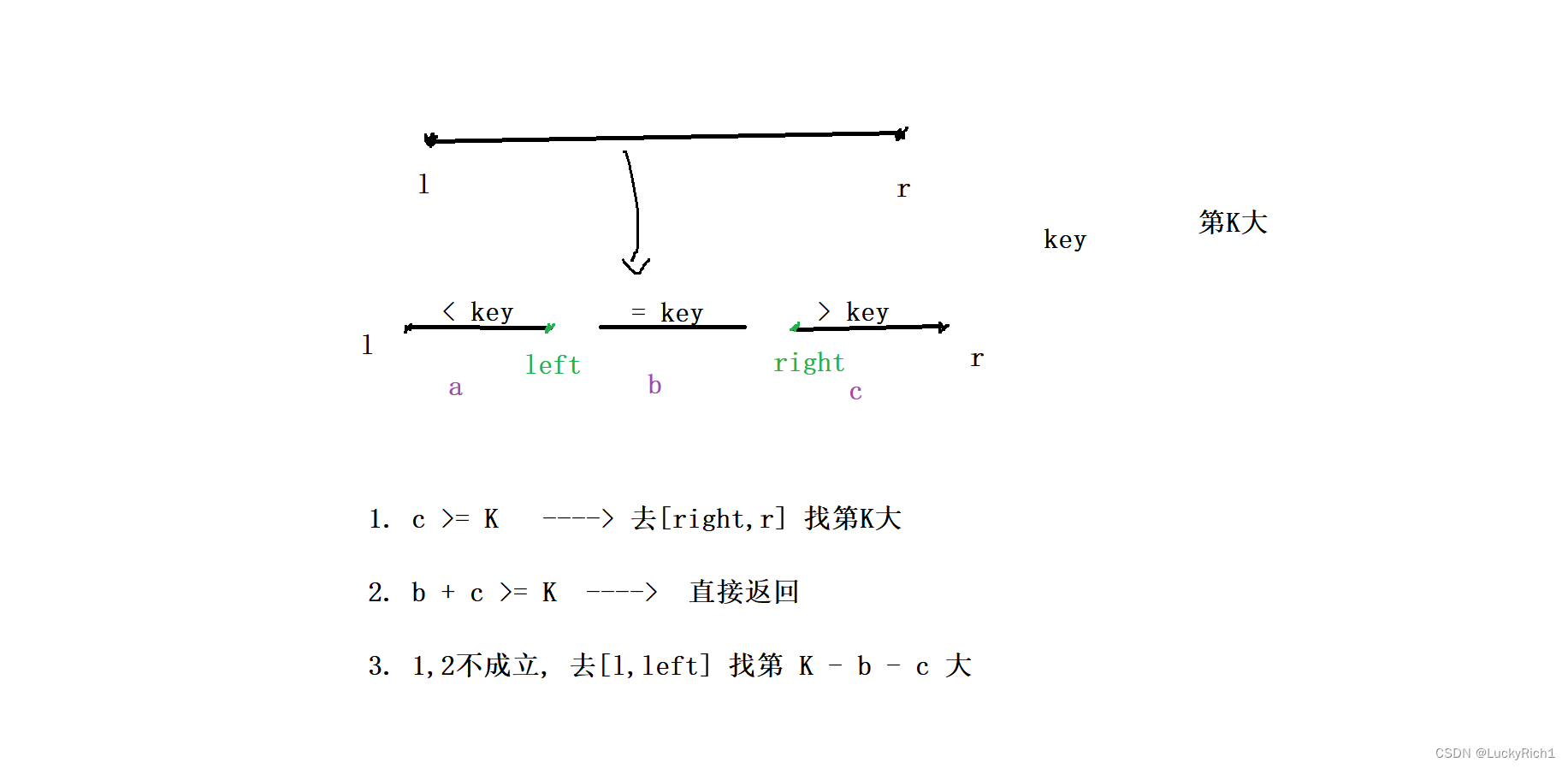
此时就分三种情况讨论:
因为求第K大,所以可以先考虑右边区域,因为右边区域都是大元素聚集地,第K大最有可能在右边区域。
- 第一种情况:如果第K大是落在右边区域,此时 c >= K,因为c表示大元素有多少个,而K表示找第K大的元素。如果 c >= K ,那第K大一定是落在右边区域。此时我们仅需到[right,r],找第K大。
- 第二种情况:如果到了第二情况那第一种情况一定是不成立的。如果第K大是落在中间区域,此时 b + c >= K,又因为第一种情况不满足,所有第K大一定是落在中间区域。此时就找到了也不用递归了。直接返回就可以。
- 第三种情况:第一、第二种情况全部不成立,第K大一定落在左边区域,去**[l,left]找**,但是此时并不是去找第K大了,本来是想在整个区间找第K大,但是第K大元素确定不在中间区域和右边区域,中间和右边区域都要被抛弃,此时去找左边区间找的是第 K - b - c 大的元素
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand((unsigned int)time(nullptr));return QuickSort(nums,0,nums.size()-1,k);}int QuickSort(vector<int>& nums, int l, int r, int k){//不用考虑区间不存在的情况,因为下面的判断K落在那个区域,只要满足进入的一定是有的if(l == r) return nums[l];// 1.随机选择基准元素int key = GetRandom(nums, l, r);// 2.根据基准元素将数组分三块int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}//3.计算每个区间都有多少元素,然后选择区间递归int b = right - 1 - left , c = r - right + 1; if(c >= k) return QuickSort(nums, right, r ,k);else if(b + c >= k) return key;else return QuickSort(nums, l, left, k - b - c);}int GetRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}// int findKthLargest(vector<int>& nums, int k) {// //前k个建小堆// priority_queue<int,vector<int>,greater<int>> pq(nums.begin(),nums.begin()+k);// //N-k与堆顶元素比较,大于堆顶就入堆,再次调整成小堆// for(size_t i=k;i<nums.size();++i)// {// if(nums[i]>pq.top())// {// pq.pop();// pq.push(nums[i]);// }// }// return pq.top();// }
};
5.库存管理 III
题目链接:LCR 159. 库存管理 III
题目分析:

实际上这也是一个TopK问题,让找前K个最小元素。注意返回结果并不考虑顺序问题。
算法原理:
解法一:排序 ,时间复杂度O(nlogn)
解法二:堆 ,时间复杂度O(nlogk)
解法三:快速选择算法,时间复杂度O(n)
数组分三块+随机选择基准元素。
选择一个基准元素key,将数组分成< key , = key ,> key 三块区域。找前K个最小的元素,落在三个区域中任何一个。统计除每个区域元素个数,然后选择去那个区域找。
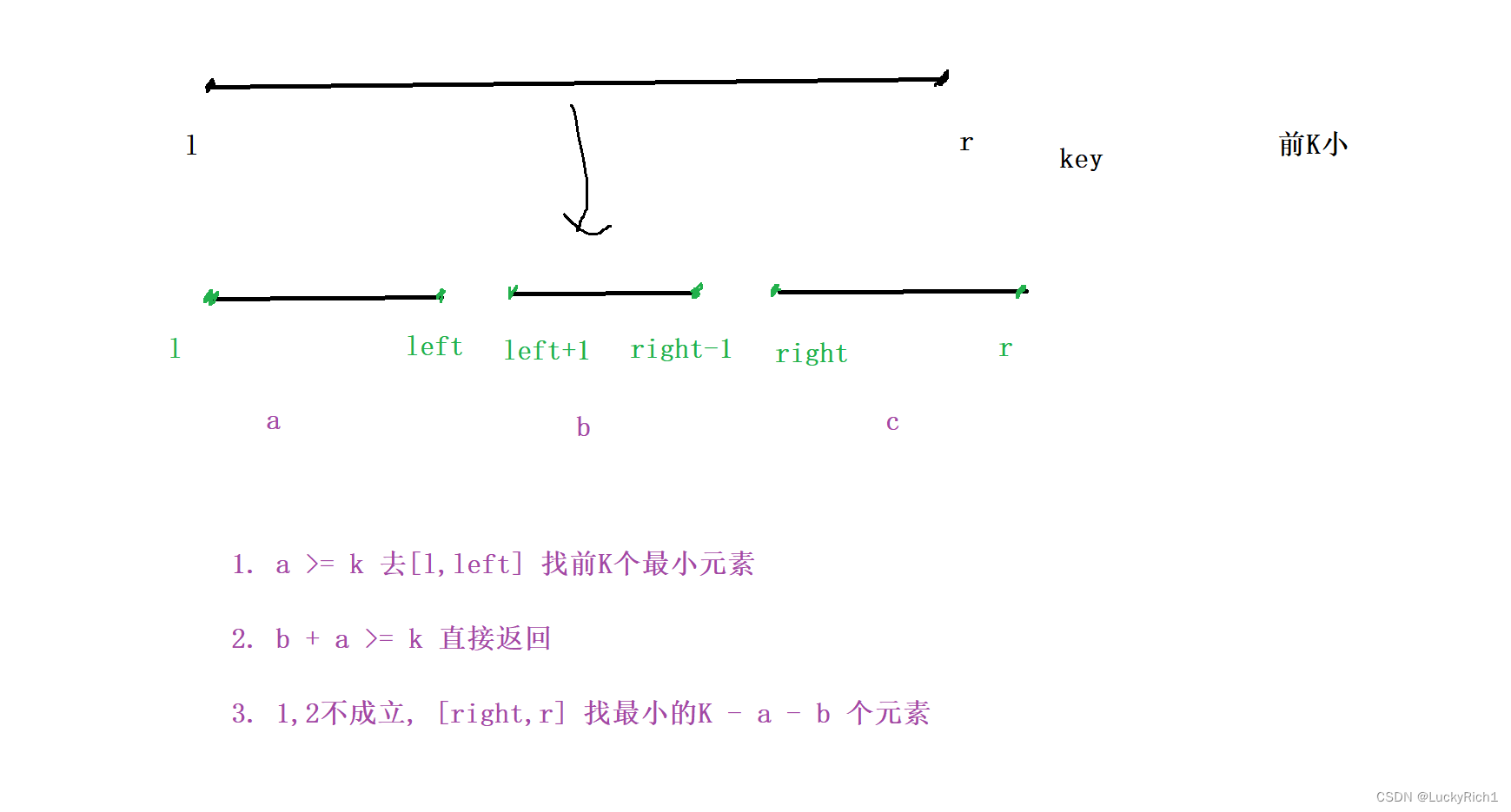
分三种情况:
因为前K下最小元素最有可能出现在左边区域,因此先判断左边区域
- a >= K ,去[l,left] 找前K个最小元素
- b + a >= K ,直接返回
- 1、2都不成立,去[right,r] 找 K - a - b 个最小元素
class Solution {
public:vector<int> inventoryManagement(vector<int>& nums, int k) {srand((unsigned int)time(nullptr));QuickSort(nums, 0, nums.size() - 1, k);return {nums.begin(),nums.begin() + k};}void QuickSort(vector<int>& nums, int l, int r, int k){if(l >= r) return;// 1. 随机选择基准元素int key = GetRandom(nums, l, r);// 2. 数组分三块int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}// 3. 分情况讨论int a = left - l + 1, b = right - left - 1;if(a >= k) QuickSort(nums, l, left, k);else if(a + b >= k) return;else QuickSort(nums, right, r, k - a - b);}int GetRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}
};
相关文章:

【基础算法总结】分治—快排
分治—快排 1.分治2.颜色分类3.排序数组4.数组中的第K个最大元素5.库存管理 III 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励,我们一起努力吧!😃😃 1.分治 分治…...
[C++]——同步异步日志系统(1)
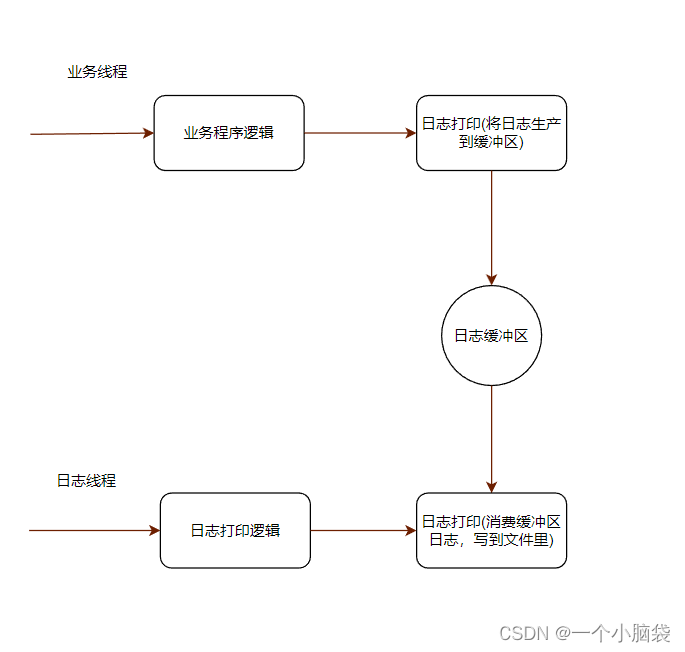
同步异步日志系统 一、项⽬介绍二、开发环境三、核心技术四、环境搭建五、日志系统介绍5.1 为什么需要日志系统5.2 日志系统技术实现5.2.1 同步写日志5.2.2 异步写日志 日志系统: 日志:程序在运行过程中,用来记录程序运行状态信息。 作用&…...

python 第6册 辅助excel 002 批量创建非空白的 Excel 文件
---用教授的方式学习 此案例主要通过使用 while 循环以及 openpyxl. load_workbook()方法和 Workbook 的 save()方法,从而实现在当前目录中根据已经存在的Excel 文件批量创建多个非空白的Excel 文件。当运行此案例的Python 代码(A002.py 文件࿰…...
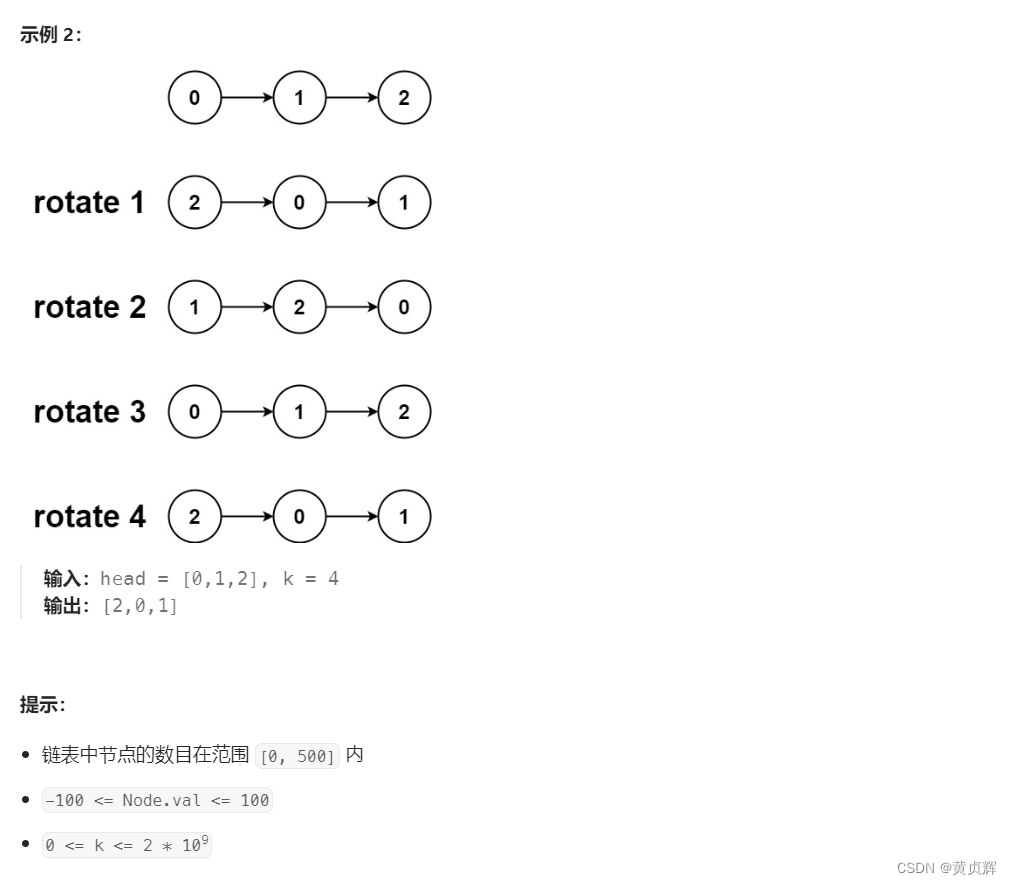
力扣61. 旋转链表(java)
思路:用快慢指针找到最后链表k个需要移动的节点,然后中间断开节点,原尾节点连接原头节点,返回新的节点即可; 但因为k可能比节点数大,所以需要先统计节点个数,再取模,看看k到底需要移…...
智慧园区综合平台解决方案PPT(75页)
## 智慧园区的理解 ### 从园区1.0到园区4.0的演进 1. 园区1.0:以土地经营为主,成本驱动,提供基本服务。 2. 园区2.0:服务驱动,关注企业成长,提供增值服务。 3. 园区3.0:智慧型园区ÿ…...

Python只读取Excel文件的一部分数据,比如特定范围的行和列?
如何只读取Excel文件的一部分数据,比如特定范围的行和列? 在Python中,如果你只想读取Excel文件的特定范围,可以使用以下方法: pandas: Pandas是一个强大的数据处理库,它有一个内置函数read_excel()用于读…...
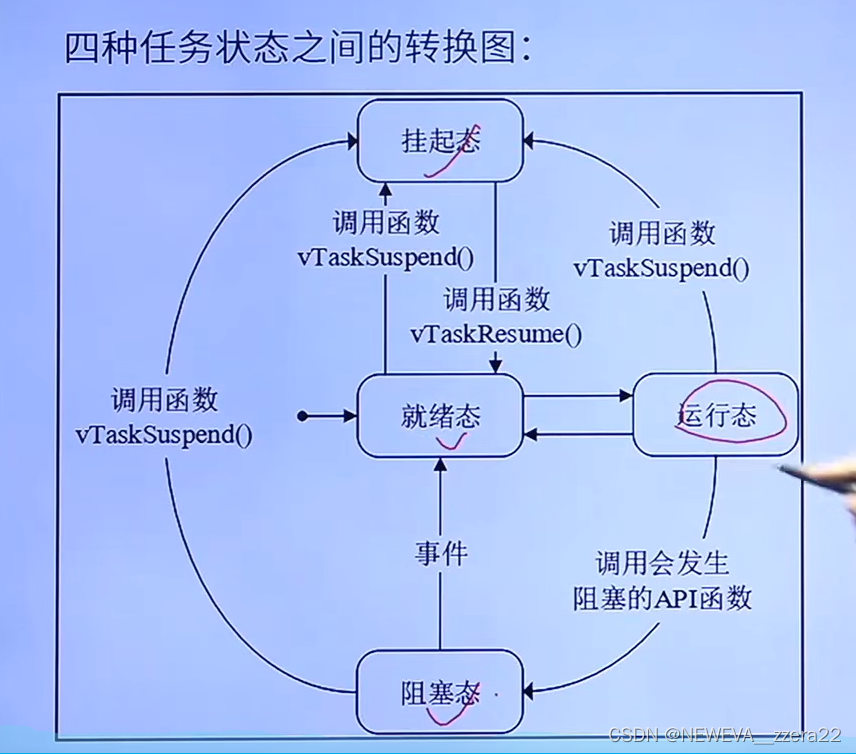
快速入门FreeRTOS心得(正点原子学习版)
对于FreeROTS,我第一反应想到的就是通信里的TDM(时分多址)。不同任务给予分配不同的时间间隔,也就是任务之间在每个timeslot都在来回切换。 这里有重要的一点,就是中断要短小,优先级是自高到底进行打断。 …...

【博主推荐】HTML5实现简洁好看的个人简历网页模板源码
文章目录 1.设计来源1.1 主界面1.2 关于我界面1.3 工作经验界面1.4 学习教育界面1.5 个人技能界面1.6 专业特长界面1.7 朋友评价界面1.8 获奖情况界面1.9 联系我界面 2.效果和源码2.1 动态效果2.2 源代码 源码下载万套模板,程序开发,在线开发,…...

Android应用安装过程
Android 系统源码源码-应用安装过程 Android 中应用安装的过程就是解析 AndroidManifest.xml 的过程,系统可以从 Manifest 中得到应用程序的相关信息,比如 Activity、Service、Broadcast Receiver 和 ContentProvider 等。这些工作都是由 PackageManage…...

Word中输入文字时,后面的文字消失
当在Word中输入文字时,如果发现后面的文字消失,通常是由以下3个原因造成的: 检查Insert键状态:首先确认是否误按了Insert键。如果是,请再次按下Insert键以切换回插入模式。在插入模式下,新输入的文字会插入…...

【LeetCode】合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 解题思路 水题,主要用于后面的链表的归并排序做了该题 AC代码 # Definition for singly-linked list. # class ListNode: # def __init__(self, val0, nex…...

分子AI预测赛Task1笔记
分子AI预测赛Task1笔记 实践步骤:跑通baseline → 尝试个人idea→尝试进阶baseline 一、跑通baseline 1、应当先下载数据库 下载相应的数据库 !pip install lightgbm openpyxl2、训练模型并预测结果 首先要导入相应的库和方法类,如pandas等 # 1. …...
ubuntu 安装并启用 samba
环境:ubuntu server 24.04 步骤如下: sudo apt update sudo apt install samba修改配置文件: sudo vi /etc/samba/smb.conf新增内容: [username]path /home/[username]available yesvalid users [username]read only nobrow…...

atcoder ABC 357-D题详解
atcoder ABC 357-D题详解 Problem Statement For a positive integer N, let VN be the integer formed by concatenating N exactly N times. More precisely, consider N as a string, concatenate N copies of it, and treat the result as an integer to get VN. For…...
从单一到多元:EasyCVR流媒体视频汇聚技术推动安防监控智能升级
随着科技的飞速发展,视频已成为我们日常生活和工作中的重要组成部分。尤其在远程办公、在线教育、虚拟会议等领域,视频的应用愈发广泛。为了满足日益增长的视频需求,流媒体视频汇聚融合技术应运而生,它不仅改变了传统视频的观看和…...
JSON数据的回写)
Spring MVC数据绑定和响应——数据回写(二)JSON数据的回写
项目中已经导入了Jackson依赖,可以先调用Jackson的JSON转换的相关方法,将对象或集合转换成JSON数据,然后通过HttpServletResponse将JSON数据写入到输出流中完成回写,具体步骤如下。 1、修改文件DataController.java,在…...
怎么快速给他人分享图片?扫描二维码看图的简单做法
现在通过二维码来查看图片是一种很常见的方法,通过二维码来查看图片不仅能够减少对手机存储空间的占用,而且获取图片变得更加方便快捷,只需要扫码就能够查看图片,有利于图片的展现。很多的场景中都有图片二维码的应用,…...
【UML用户指南】-26-对高级行为建模-状态图
目录 1、概念 2、组成结构 3、一般用法 4、常用建模技术 4.1、对反应型对象建模 一个状态图显示了一个状态机。在为对象的生命期建模中 活动图展示的是跨过不同的对象从活动到活动的控制流 状态图展示的是单个对象内从状态到状态的控制流。 在UML中,用状态图…...
解决VSCode无法用ssh连接远程服务器的问题
原因: 因为windows自带的ssh无法连接远程服务器,需要用git底下的ssh.exe。 搜了很久,试过很多方法,包括替换掉环境变量中的ssh,但是都无效,最后发现是要在VSCode中配置需要使用哪个ssh.exe。 步骤&#…...
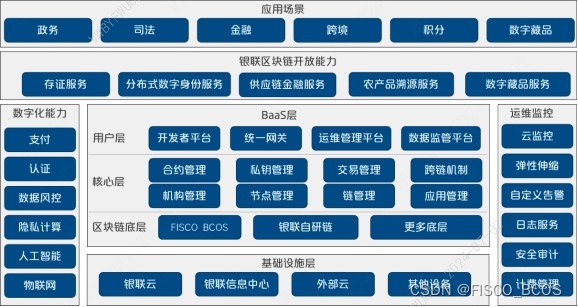
【区块链+基础设施】银联云区块链服务 | FISCO BCOS应用案例
为了顺应区块链基础设施化的发展趋势,中国银联推出了银联云区块链服务——UPBaaS,为金融行业采用区块链 技术提出了解决方案,微众银行为平台提供 FISCO BCOS 区块链开源技术支持。通过银联云区块链服务,用户可 以用可视化的方式创…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
