代码随想录-Day45
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
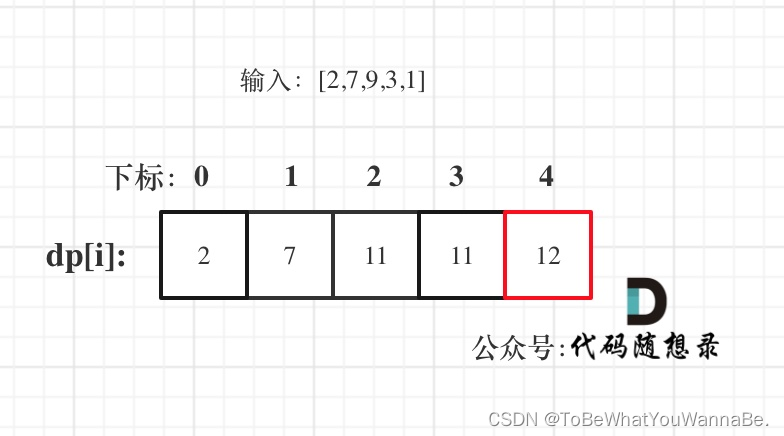
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
方法一:
// 动态规划
class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) return 0;if (nums.length == 1) return nums[0];int[] dp = new int[nums.length];dp[0] = nums[0];dp[1] = Math.max(dp[0], nums[1]);for (int i = 2; i < nums.length; i++) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[nums.length - 1];}
}
这段代码是一个Java类,实现了一个名为Solution的类,其中包含一个名为rob的公共方法。这个方法使用动态规划算法来解决“打家劫舍”问题(LeetCode上的第198题)。这个问题描述的是:你是一个小偷,沿街有一排房子,每个房子都有一定数量的钱。相邻的房子有防盗系统连接,如果两间相邻的房子都被抢劫,则会自动联系警察。给定一个整数数组 nums,代表每间房子存放的金额,返回在不触动警报的情况下,你能抢劫到的最大金额。
在这个方法中:
- 首先检查输入数组是否为空或长度为0,如果是,则返回0。
- 如果数组长度为1,直接返回该元素的值。
- 初始化一个与输入数组长度相同的动态规划数组
dp,用于存储计算过程中的最大值。 - 设置
dp[0]和dp[1]的初始值。 - 使用for循环遍历输入数组,从下标2开始,对于每个位置i,
dp[i]等于dp[i - 1]和dp[i - 2] + nums[i]中的较大值。 - 最后返回
dp数组的最后一个元素,即为最大可抢金额。
这种方法的时间复杂度是O(n),空间复杂度也是O(n),其中n是输入数组的长度。不过,可以进一步优化空间复杂度至O(1),只用两个变量来替代整个dp数组。
方法二:
// 使用滚动数组思想,优化空间
// 分析本题可以发现,所求结果仅依赖于前两种状态,此时可以使用滚动数组思想将空间复杂度降低为3个空间
class Solution {public int rob(int[] nums) {int len = nums.length;if (len == 0) return 0;else if (len == 1) return nums[0];else if (len == 2) return Math.max(nums[0],nums[1]);int[] result = new int[3]; //存放选择的结果result[0] = nums[0];result[1] = Math.max(nums[0],nums[1]);for(int i=2;i<len;i++){result[2] = Math.max(result[0]+nums[i],result[1]);result[0] = result[1];result[1] = result[2];}return result[2];}
}
这段代码同样实现了“打家劫舍”问题的解决方案,但采用了滚动数组的思想来优化空间复杂度。在原版的动态规划解法中,我们使用了一个与输入数组等长的数组来保存中间状态。然而,通过观察动态转移方程,我们可以发现当前状态只依赖于前两个状态,因此没有必要保存所有的历史状态,只需要保留最近的两个状态即可。
在这个优化版本中:
- 首先进行边界条件判断,处理输入数组为空、只有一个元素或只有两个元素的情况。
- 创建一个长度为3的数组
result来保存最近三个状态的值。 - 初始化
result[0]和result[1]的值。 - 使用for循环遍历输入数组,从下标2开始,对于每个位置i,更新
result[2]为result[0] + nums[i]和result[1]中的较大值。 - 在每次迭代结束后,将
result[0]更新为上一轮的result[1],将result[1]更新为当前轮的result[2]。 - 循环结束后,
result[2]即为最大可抢金额。
这种方法的空间复杂度被优化到了O(1),因为无论输入数组的长度如何,都只需要常数级别的额外空间。时间复杂度仍然是O(n),其中n是输入数组的长度。这种优化在处理大规模数据时尤为重要,因为它减少了内存使用,提高了程序的效率。
方法三:
// 进一步对滚动数组的空间优化 dp数组只存与计算相关的两次数据
class Solution {public int rob(int[] nums) {if (nums.length == 1) {return nums[0];}// 初始化dp数组// 优化空间 dp数组只用2格空间 只记录与当前计算相关的前两个结果int[] dp = new int[2];dp[0] = nums[0];dp[1] = Math.max(nums[0],nums[1]);int res = 0;// 遍历for (int i = 2; i < nums.length; i++) {res = Math.max((dp[0] + nums[i]) , dp[1] );dp[0] = dp[1];dp[1] = res;}// 输出结果return dp[1];}
}
这段代码进一步优化了“打家劫舍”问题的解决方案,其目标是将空间复杂度降至最低。这里使用了一个长度为2的数组dp来存储动态规划过程中所需的最近两个状态,而不是之前示例中长度为3的数组。这样做的原因是,我们只需保存前两个状态的信息,就能计算出下一个状态的值。
具体来说:
- 首先处理边界情况,当输入数组长度为1时,直接返回该元素的值。
- 初始化长度为2的
dp数组,dp[0]和dp[1]分别初始化为数组的前两个元素的值。 - 声明一个变量
res用于临时存储计算结果。 - 使用for循环遍历输入数组,从下标2开始,对于每个位置i,计算
res为dp[0] + nums[i]和dp[1]中的较大值。 - 更新
dp[0]和dp[1]的值,dp[0]更新为上一轮的dp[1],dp[1]更新为当前计算得到的res。 - 循环结束后,
dp[1]即为最大可抢金额,作为最终结果返回。
这种方法的空间复杂度进一步优化到了O(1),因为我们只使用了固定大小的数组,无论输入数组的长度如何。时间复杂度仍然是O(n),其中n是输入数组的长度。这种优化策略在处理大数据量时特别有效,因为它极大地减少了内存消耗,同时保持了较高的计算效率。
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3


class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0)return 0;int len = nums.length;if (len == 1)return nums[0];return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));}int robAction(int[] nums, int start, int end) {int x = 0, y = 0, z = 0;for (int i = start; i < end; i++) {y = z;z = Math.max(y, x + nums[i]);x = y;}return z;}
}
这段代码是针对“打家劫舍 II”问题(LeetCode上的第213题)的一个解决方案。这个问题与原始的“打家劫舍”问题(LeetCode上的第198题)类似,但是添加了一个额外的约束:房子排列成一个圈,这意味着第一间房子和最后一间房子是相邻的,不能同时被抢劫。因此,解决问题的方法略有不同。
在代码中:
- 首先,检查输入数组是否为空或长度为0,如果是,则返回0。
- 如果输入数组长度为1,直接返回该元素的值。
- 然后,调用
robAction函数两次,第一次考虑从第一个元素到最后一个元素前一个(即不包括最后一个元素),第二次考虑从第二个元素到最后一个元素(即不包括第一个元素)。这是因为如果抢劫了第一个房子,就不能抢劫最后一个房子,反之亦然。 - 最后,取这两次调用
robAction函数返回值中的最大值作为最终结果,因为我们要找的是所有可能情况下的最大抢劫金额。
robAction函数是一个辅助函数,它接受一个整数数组nums以及开始和结束的索引,然后使用滚动数组思想来计算从start到end(不包括end)的最大可抢金额。具体来说:
- 初始化三个变量
x、y和z,分别表示前前一个状态、前一个状态和当前状态的最大可抢金额。 - 使用for循环遍历数组,从
start到end - 1,对于每个位置i,更新y和z的值。y被更新为上一轮的z,而z被更新为y和x + nums[i]中的较大值。 - 循环结束后,
z即为从start到end - 1的最大可抢金额。
这种方法的时间复杂度是O(n),空间复杂度是O(1),其中n是输入数组的长度。通过使用滚动数组思想,我们能够有效地减少空间使用,提高程序性能。
337. 打家劫舍 III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
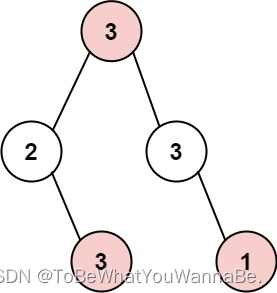
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
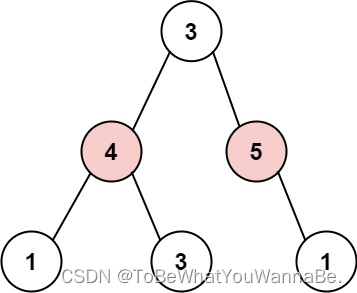
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
方法一:
class Solution {// 1.递归去偷,超时public int rob(TreeNode root) {if (root == null)return 0;int money = root.val;if (root.left != null) {money += rob(root.left.left) + rob(root.left.right);}if (root.right != null) {money += rob(root.right.left) + rob(root.right.right);}return Math.max(money, rob(root.left) + rob(root.right));}
这段代码是解决“打家劫舍 III”问题(LeetCode上的第337题)的一种尝试,但使用了简单的递归方法,这种方法虽然逻辑上正确,但在实际运行时会遇到性能问题,特别是在树的规模较大时,可能会导致超时错误。
在这个问题中,你需要在一个二叉树中最大化你的收益,但你不能抢劫任何具有直接父子关系的节点。给定一棵以TreeNode表示的二叉树的根节点root,返回你能获得的最大金额。
代码中定义的rob方法采用递归方式解决这个问题:
- 首先,检查根节点是否为空,如果是,则返回0,因为没有节点可以抢劫。
- 然后,计算抢劫当前节点所能获得的金额
money,即当前节点的值加上其左子树和右子树的孙子节点所能提供的最大金额。 - 接着,递归地计算左子树和右子树不抢劫根节点所能提供的最大金额。
- 最后,返回
money和左右子树不抢劫根节点所能提供的最大金额的较大值。
然而,这种方法存在重复计算的问题,即同一子树会被多次计算,导致时间复杂度过高。为了优化这个问题,可以使用动态规划或记忆化搜索的方法来避免重复计算,将已经计算过的子树的结果缓存起来,从而显著提高算法的效率。
例如,可以使用一个哈希表或者在TreeNode结构中增加一个额外的字段来存储每个节点所能提供的最大金额,这样就可以避免重复计算,将时间复杂度降低到O(n),其中n是树中节点的数量。
方法二:
// 2.递归去偷,记录状态// 执行用时:3 ms , 在所有 Java 提交中击败了 56.24% 的用户public int rob1(TreeNode root) {Map<TreeNode, Integer> memo = new HashMap<>();return robAction(root, memo);}int robAction(TreeNode root, Map<TreeNode, Integer> memo) {if (root == null)return 0;if (memo.containsKey(root))return memo.get(root);int money = root.val;if (root.left != null) {money += robAction(root.left.left, memo) + robAction(root.left.right, memo);}if (root.right != null) {money += robAction(root.right.left, memo) + robAction(root.right.right, memo);}int res = Math.max(money, robAction(root.left, memo) + robAction(root.right, memo));memo.put(root, res);return res;}
这段代码是对“打家劫舍 III”问题(LeetCode上的第337题)的优化解法,通过引入记忆化搜索(也称为备忘录方法)来避免重复计算,从而显著提高了算法的效率。
在代码中:
- 定义了一个
HashMap叫做memo,用来存储已经计算过的节点及其对应的最大可抢金额,以此来避免重复计算。 rob1方法是对外提供的接口,它接收树的根节点作为参数,并返回最大可抢金额。它首先创建一个空的memo哈希表,然后调用robAction方法来计算结果。robAction方法是核心的递归函数,它接收一个树节点和memo哈希表作为参数。如果当前节点已经在memo中,直接返回对应的值;否则,计算当前节点的最大可抢金额,将结果存储到memo中,并返回。
具体来说,在robAction方法中:
- 如果节点为空,返回0。
- 如果
memo中已经存在当前节点的值,直接返回该值。 - 计算抢劫当前节点所能获得的金额
money,即当前节点的值加上其左子树和右子树的孙子节点所能提供的最大金额。 - 递归地计算左子树和右子树不抢劫根节点所能提供的最大金额。
- 将计算出的最大金额
res存储到memo中,并返回。
通过这种方式,每个节点只被计算一次,避免了原始递归方法中的大量重复计算,从而将时间复杂度降低到O(n),其中n是树中节点的数量。空间复杂度主要由memo哈希表决定,最坏情况下为O(n),即所有节点都需要被存储。这种优化使得算法在处理大规模数据时表现更佳,避免了超时错误。
方法三:
// 3.状态标记递归// 执行用时:0 ms , 在所有 Java 提交中击败了 100% 的用户// 不偷:Max(左孩子不偷,左孩子偷) + Max(右孩子不偷,右孩子偷)// root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +// Math.max(rob(root.right)[0], rob(root.right)[1])// 偷:左孩子不偷+ 右孩子不偷 + 当前节点偷// root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;public int rob3(TreeNode root) {int[] res = robAction1(root);return Math.max(res[0], res[1]);}int[] robAction1(TreeNode root) {int res[] = new int[2];if (root == null)return res;int[] left = robAction1(root.left);int[] right = robAction1(root.right);res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);res[1] = root.val + left[0] + right[0];return res;}
}
这段代码提供了一种解决“打家劫舍 III”问题(LeetCode上的第337题)的高效方法,采用了状态标记的递归策略。这种方法不仅避免了重复计算,还通过在每次递归调用中返回两个状态信息(偷与不偷的最大金额),从而简化了后续的决策过程。
在代码中:
rob3方法是主入口,它调用robAction1方法并返回最终的最大可抢金额。robAction1方法返回一个长度为2的数组,其中第一个元素表示不抢劫当前节点时的最大金额,第二个元素表示抢劫当前节点时的最大金额。robAction1方法实现了核心的递归逻辑,它接收一个树节点作为参数,递归地计算其左右子树的状态,并基于这些状态计算当前节点的两个状态。
具体来说,在robAction1方法中:
- 如果节点为空,返回一个全是0的数组。
- 对于当前节点,递归地获取其左右子树的状态信息。
- 根据左右子树的状态信息,计算当前节点的两个状态:
res[0]表示不抢劫当前节点时的最大金额,等于左右子树中偷与不偷的最大金额之和的较大值。res[1]表示抢劫当前节点时的最大金额,等于当前节点的值加上左右子树不抢劫时的最大金额之和。
最后,rob3方法返回robAction1方法返回的数组中两个元素的较大值,即整个树的最大可抢金额。
这种方法的时间复杂度为O(n),空间复杂度也为O(n),其中n是树中节点的数量。相比于原始的简单递归方法,这种方法通过避免重复计算显著提高了效率,而且通过返回两个状态信息简化了决策过程,使得代码更加简洁和易于理解。
相关文章:

代码随想录-Day45
198. 打家劫舍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个…...
Rust Eq 和 PartialEq
Eq 和 PartialEq 在 Rust 中,想要重载操作符,你就需要实现对应的特征。 例如 <、<、> 和 > 需要实现 PartialOrd 特征: use std::fmt::Display;struct Pair<T> {x: T,y: T, }impl<T> Pair<T> {fn new(x: T, y: T) ->…...

思考如何学习一门编程语言?
一、什么是编程语言 编程语言是一种用于编写计算机程序的人工语言。通过编程语言,程序员可以向计算机发出指令,控制计算机执行各种任务和操作。编程语言由一组语法规则和语义规则组成,这些规则定义了如何编写代码以及代码的含义。 编程语言…...
顺序串算法库构建
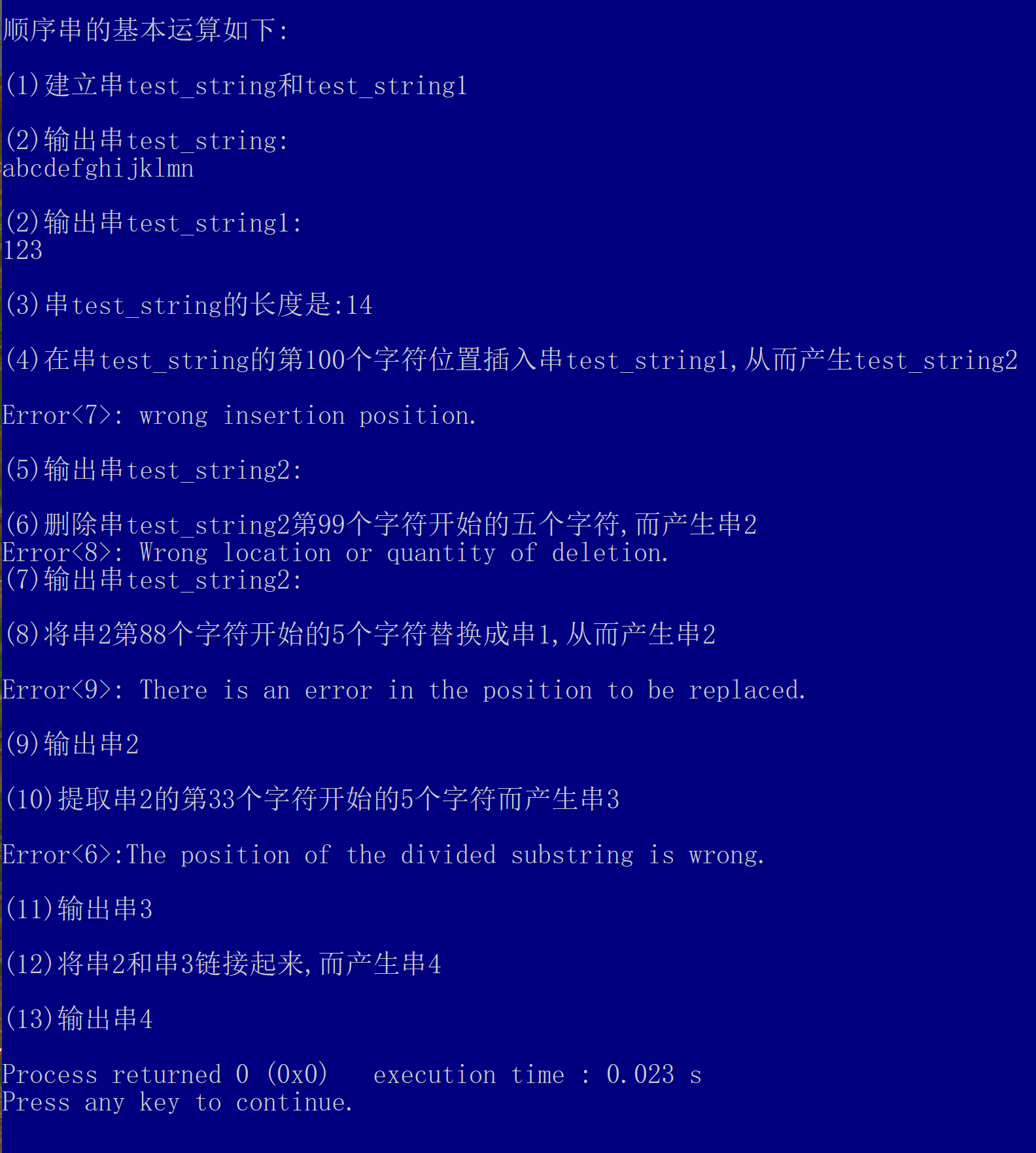
学习贺利坚老师顺序串算法库 数据结构之自建算法库——顺序串_创建顺序串s1,创建顺序串s2-CSDN博客 本人详细解析博客 串的概念及操作_串的基本操作-CSDN博客 版本更新日志 V1.0: 在贺利坚老师算法库指导下, 结合本人详细解析博客思路基础上,进行测试, 加入异常弹出信息 v1.0补…...
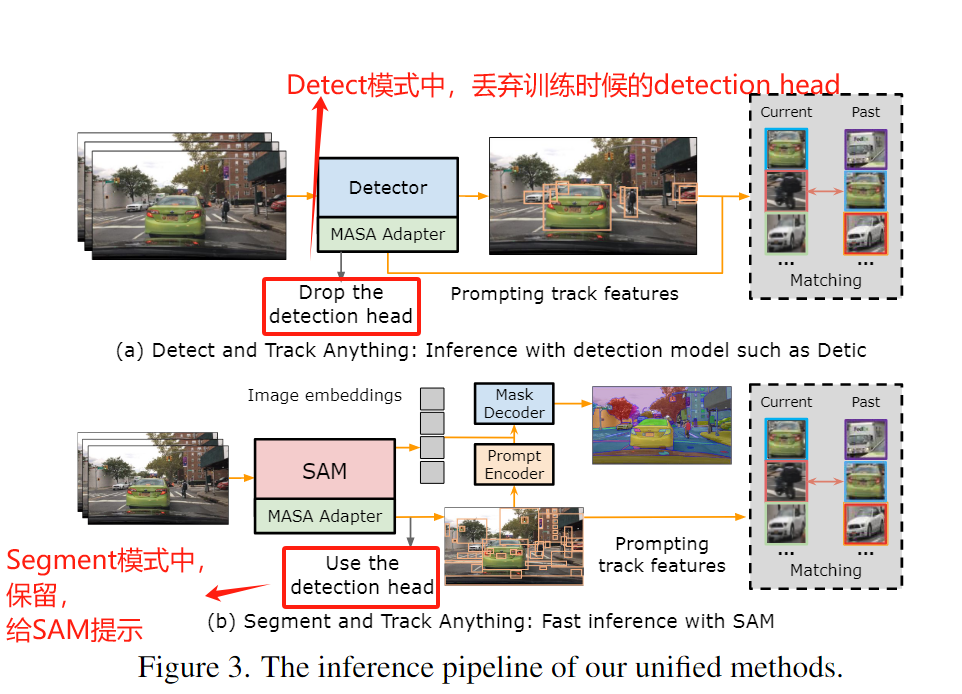
[论文阅读笔记33] Matching Anything by Segmenting Anything (CVPR2024 highlight)
这篇文章借助SAM模型强大的泛化性,在任意域上进行任意的多目标跟踪,而无需任何额外的标注。 其核心思想就是在训练的过程中,利用strong augmentation对一张图片进行变换,然后用SAM分割出其中的对象,因此可以找到一组图…...
阿里Nacos下载、安装(保姆篇)
文章目录 Nacos下载版本选择Nacos安装Windows常见问题解决 更多相关内容可查看 Nacos下载 Nacos官方下载地址:https://github.com/alibaba/nacos/releases 码云拉取(如果国外较慢或者拉取超时可以试一下国内地址) //国外 git clone https:…...

四、golang基础之defer
文章目录 一、定义二、作用三、结果四、recover错误拦截 一、定义 defer语句被用于预定对一个函数的调用。可以把这类被defer语句调用的函数称为延迟函数。 二、作用 释放占用的资源捕捉处理异常输出日志 三、结果 如果一个函数中有多个defer语句,它们会以LIFO…...

机器人----四元素
四元素 四元素的大小 [-1,1] 欧拉角转四元素...

IBM Spectrum LSF Application Center 提供单一界面来管理应用程序、用户、资源和数据
IBM Spectrum LSF Application Center 提供单一界面来管理应用程序、用户、资源和数据 亮点 ● 简化应用程序管理 ● 提高您的工作效率 ● 降低资源管理的复杂性 ● 深入了解流程 IBM Spectrum LSF Application Center 为集群用户和管理员提供了一个灵活的、以应用为中心的界…...
如何选择品牌推广公司?哪家好?收费标准及评价!
不管是什么品牌,推广对公司的成败起了很关键的作用。然而,面对市面上琳琅满目的品牌推广公司,如何选择一家既熟悉又靠谱的公司,成为许多企业主面临的难题。 作为一家手工酸奶品牌的创始人,目前全国也复制了100多家门店…...
JDeveloper 12C 官网下载教程
首先、我们要登录Oracle官网 Oracle 甲骨文中国 | 云应用和云平台 登录进去如果不是中文可以点击右上角带有国旗的图标就行更改,选择一个你能看懂的文字。 然后,点击“资源”—点击“开发人员下载” 然后,点击“开发工具” 这里有很多工具可…...
)
中英双语介绍美国的州:印第安纳州(Indiana)
中文版 印第安纳州简介 印第安纳州位于美国中西部地区,是一个以其农业、制造业和体育文化而著称的州。以下是对印第安纳州的详细介绍,包括其地理位置、人口、经济、教育、文化和主要城市。 地理位置 印第安纳州东临俄亥俄州,北接密歇根州…...

Flink实现准确和高效流处理的关键问题
时间相关: Watermark 水位线 水位线是插入到数据流中的一个标记,可以认为是一个特殊的数据。水位线主要的内容是一个时间戳,用来表示当前事件时间的进展。水位线是基于数据的时间戳生成的。水位线的时间戳必须单调递增,以确保任务的事件时间时钟一直向前推进,进展。水位线…...

isidentifier()方法——判断字符串是否为合法的Python标识符或变量名
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 语法参考 isidentifier()方法用于判断字符串是否是有效的Python标识符,还可以用来判断变量名是否合法。isidentifier()方法的语法格式如…...
)
天猫商品列表数据接口(Tmall.item_search)
天猫平台商品列表数据接口(taobao.item_search)是天猫开放平台提供的一个API接口,用于获取天猫平台上的商品列表数据。通过该接口,用户可以获取到商品的名称、价格、销量、评价等信息。下面将具体介绍这个接口的各个方面ÿ…...
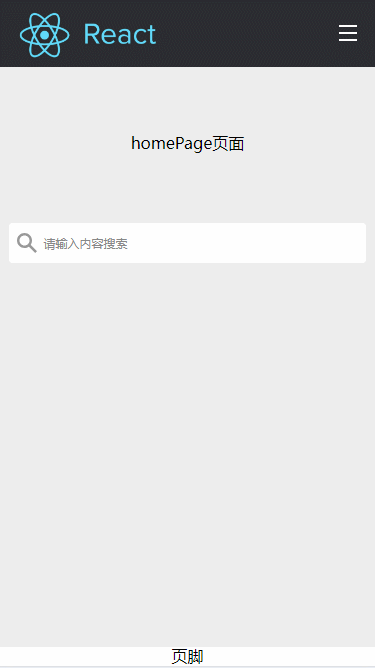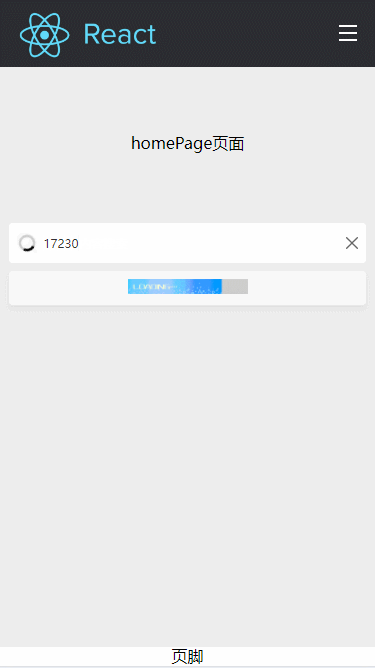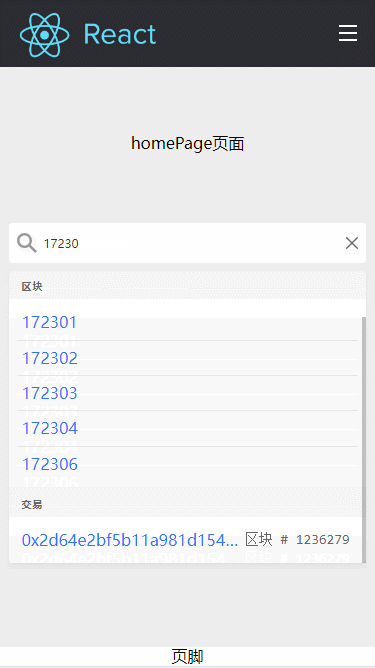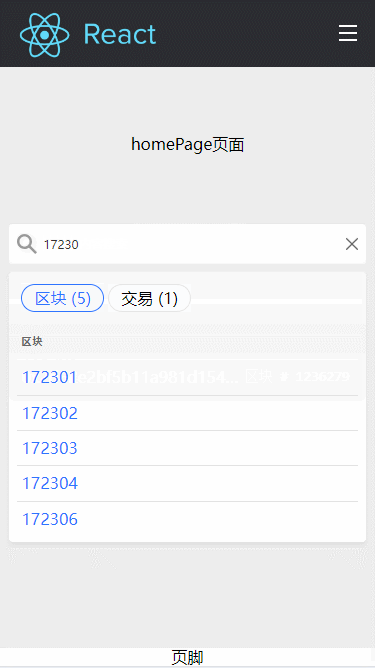
React+TS前台项目实战(二十一)-- Search业务组件封装实现全局搜索
文章目录 前言一、Search组件封装1. 效果展示2. 功能分析3. 代码详细注释4. 使用方式 二、搜索结果展示组件封装1. 功能分析2. 代码详细注释 三、引用到文件,自行取用总结 前言 今天,我们来封装一个业务灵巧的组件,它集成了全局搜索和展示搜…...
SEO与AI的结合:如何用ChatGPT生成符合搜索引擎优化的内容
在当今数字时代,搜索引擎优化(SEO)已成为每个网站和内容创作者都必须掌握的一项技能。SEO的主要目标是通过优化内容,使其在搜索引擎结果页面(SERP)中排名更高,从而吸引更多的流量。然而…...

【信息系统项目管理师知识点速记】组织通用管理:知识管理
23.3 知识管理 23.3.1 知识管理基础 知识管理是通过利用各种知识和技术手段,帮助组织和个人生产、分享、应用和创新知识,以形成知识优势并在个人、组织、业务目标、经济绩效和社会效益方面产生价值的过程。它能为组织带来知识增值,创造新的价值,提升决策效能和水平,是提…...
CM-UNet: Hybrid CNN-Mamba UNet for Remote Sensing Image Semantic Segmentation
论文:CM-UNet: Hybrid :CNN-Mamba UNet for Remote Sensing Image Semantic Segmentation 代码:https://github.com/XiaoBuL/CM-UNet Abstrcat: 由于大规模图像尺寸和对象变化,当前基于 CNN 和 Transformer 的遥感图像语义分割方…...
DP:子序列问题
文章目录 什么是子序列子序列的特点举例说明常见问题 关于子序列问题的几个例题1.最长递增子序列2.摆动序列3.最长递增子序列的个数4.最长数对链5.最长定差子序列 总结 什么是子序列 在计算机科学和数学中,子序列(Subsequence)是指从一个序列…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
