【数据结构 - 时间复杂度和空间复杂度】
文章目录
- <center>时间复杂度和空间复杂度
- 算法的复杂度
- 时间复杂度
- 大O的渐进表示法
- 常见时间复杂度计算举例
- 空间复杂度
- 实例
时间复杂度和空间复杂度
算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
常见时间复杂度计算举例
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
- 实例1基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
- 实例2基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
- 实例3基本操作执行了10次,通过推导大O阶方法,时间复杂度为 O(1)
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}
- 实例1使用了常数个额外空间,所以空间复杂度为 O(1)
- 实例2动态开辟了N个空间,空间复杂度为 O(N)
- 实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
相关文章:

【数据结构 - 时间复杂度和空间复杂度】
文章目录 <center>时间复杂度和空间复杂度算法的复杂度时间复杂度大O的渐进表示法常见时间复杂度计算举例 空间复杂度实例 时间复杂度和空间复杂度 算法的复杂度 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏&…...

telegram支付
今天开始接入telegram支付,参考教程这个是telegram的官方说明,详细介绍了机器人支付API。 文章公开地址 新建机器人 因为支付是一个单独的系统,所以在做支付的时候单独创建了一个bot,没有用之前的bot了,特意这样将其分开。创建bot的方法和之前不变,这里不过多介绍。 获…...

elasticsearch-6.8.23的集群搭建过程
三个节点的 ElasticSearch 集群搭建步骤 准备三台机器:28.104.87.98、28.104.87.100、28.104.87.101 和 ElasticSearch 的安装包 elasticsearch-6.8.23.tar.gz ----------------------------- 28.104.87.98,使用 root 用户操作 ----------------------…...

javascript输出语法
javascript输出有三种方式 一种是弹窗输出,就是网页弹出一个对话框,弹出输出内容 语法是aler(内容) 示例代码如下 <body> <script> alert(你好); </script> </body> 这段代码运行后网页会出现一个对话框,弹出你…...
仓库管理系统26--权限设置
原创不易,打字不易,截图不易,多多点赞,送人玫瑰,留有余香,财务自由明日实现 1、权限概述 在应用软件中,通常将软件的功能分为若干个子程序,通过主程序调用。那么,通过…...

d3dx9_43.dll丢失怎么解决?d3dx9_43.dll怎么安装详细教程
在使用计算机中,如果遇到d3dx9_43.dll丢失或许找不到d3dx9_43.dll无法运行打开软件怎么办?这个是非常常见问题,下面我详细介绍一下d3dx9_43.dll是什么文件与d3dx9_43.dll的各种问题以及d3dx9_43.dll丢失的多个解决方法! 一、d3dx9…...
)
[C++] 退出清理函数解读(exit、_exit、abort、atexit)
说明:在C中,exit、_exit(或_Exit)、abort和atexit是用于控制程序退出和清理的标准库函数。下面是对这些函数的详细解读: exit 函数原型:void exit(int status);作用:exit函数用于正常退出程序…...
)
代码随想录(回溯)
组合(Leetcode77) 思路 用递归每次遍历从1-n得数,然后list来记录是不是组合到k个了,然后这个每次for循环的开始不能和上一个值的开始重复,所以设置个遍历开始索引startindex class Solution {static List<List<…...

编译原理1
NFA&DFA 在正规式的等价证明可以借助正规集,也可以通过有限自动机DFA来证明等价,以下例题是针对DFA证明正规式的等价,主要步骤是①NFA;②状态转换表; ③状态转换矩阵; ④化简DFA; 文法和语…...

【信息系统项目管理师知识点速记】组织通用管理:流程管理
23.2 流程管理 通过流程视角能够真正看清楚组织系统的本质与内在联系,理顺流程能够理顺整个组织系统。流程是组织运行体系的框架基础,流程框架的质量影响和决定了整个组织运行体系的质量。把流程作为组织运行体系的主线,配备满足流程运作需要的资源,并构建与流程框架相匹配…...

前端 JS 经典:箭头函数的意义
箭头函数是为了消除函数的二义性。 1. 二义性 函数的二义性指函数有不同的两种用法,就造成了二义性,函数的两种用法:1. 指令序列。2. 构造器 1.1 指令序列 就是调用函数,相当于将函数内部的代码再从头执行一次。 1.2 构造器 …...

Java List操作详解及常用方法
Java List操作详解及常用方法 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 什么是Java List? Java中的List是一种动态数组,它允许存…...
《mysql篇》--查询(进阶)
目录 将查询结果作为插入数据 聚合查询 聚合函数 count sum group by子句 having 联合查询 笛卡尔积 多表查询 join..on实现多表查询 内连接 外连接 自连接 子查询 合并查询 将查询结果作为插入数据 Insert into 表2 select * from 表1//将表1的查询数据插入…...

数据库-MySQL 实战项目——书店图书进销存管理系统数据库设计与实现(附源码)
一、前言 该项目非常适合MySQL入门学习的小伙伴,博主提供了源码、数据和一些查询语句,供大家学习和参考,代码和表设计有什么不恰当还请各位大佬多多指点。 所需环境 MySQL可视化工具:navicat; 数据库:MySq…...
eNSP中WLAN的配置和使用
一、基础配置 1.拓扑图 2.VLAN和IP配置 a.R1 <Huawei>system-view [Huawei]sysname R1 GigabitEthernet 0/0/0 [R1-GigabitEthernet0/0/0]ip address 200.200.200.200 24 b.S1 <Huawei>system-view [Huawei]sysname S1 [S1]vlan 100 [S1-vlan100]vlan 1…...
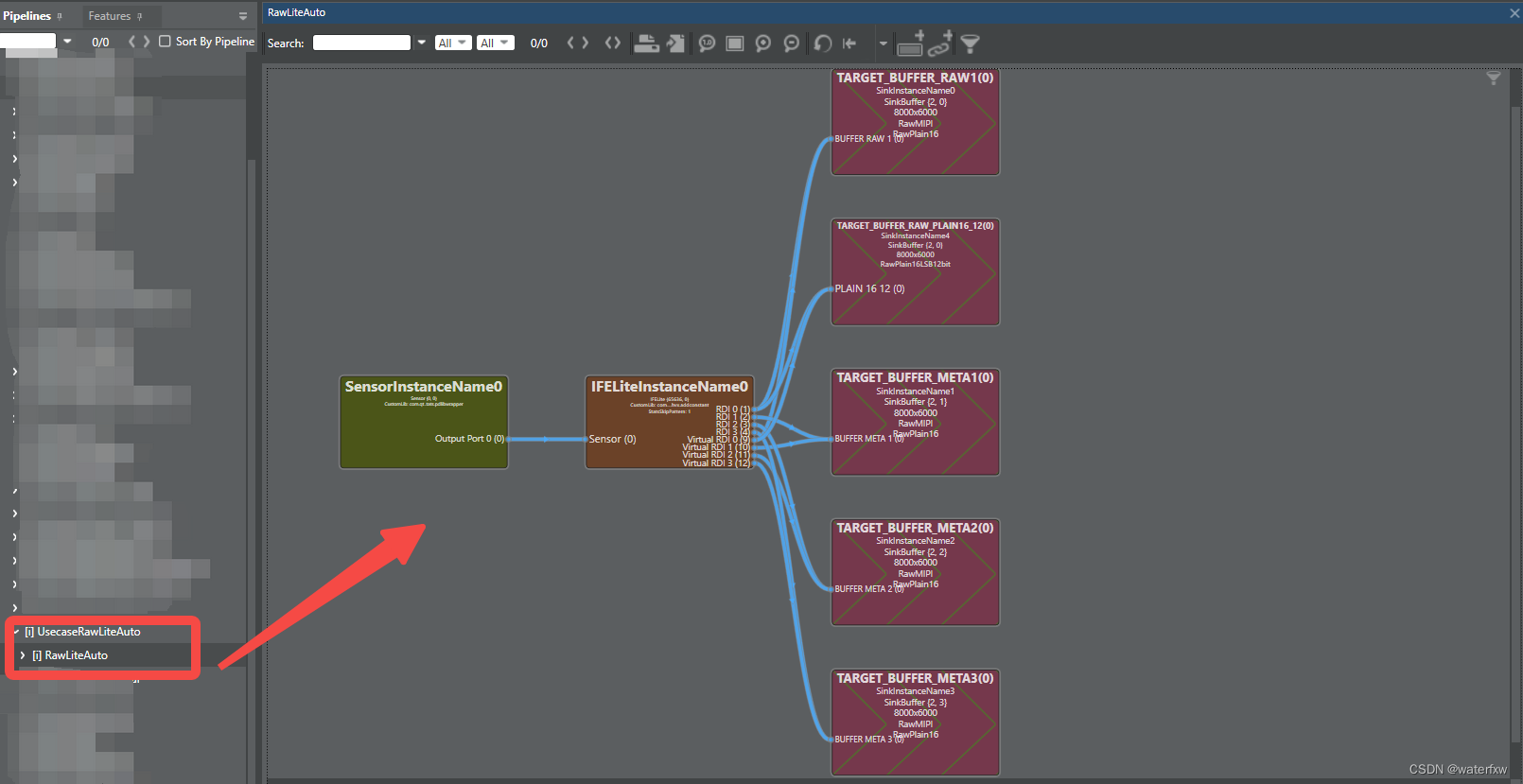
<sa8650>QCX ID16_UsecaseRawLiteAuto 使用详解
<sa8650>QCX ID16_UsecaseRawLiteAuto 使用详解 一、前言二、ID16_UsecaseRawLiteAuto拓扑图三、UsecaseRawLiteAuto拓扑图 解析3.1 camxUsecaseRawLiteAuto.xml3.2 camxRawLiteAuto.xml四、测试一、前言 我们在使用QCX时,如果由于使用的摄像头自带了ISP,那么可能不需要使…...

为什么3d重制变换模型会变形?---模大狮模型网
在当今数字技术飞速发展的时代,3D建模和动画制作已经成为影视、游戏和虚拟现实中不可或缺的一部分。然而,即使在高级的3D软件中,重制(rigging)和变换(transformation)过程中仍然会面临一个普遍的问题——模型变形。这种变形可能导致动画效果不…...

ElasticSearch中的BM25算法实现原理及应用分析
文章目录 一、引言二、BM25算法实现原理BM25算法的实现原理1. 词频(TF):2. 逆文档频率(IDF):3. 长度归一化:4. BM25评分公式: BM25算法示例 三、BM25算法在ElasticSearch中的应用分析…...
web权限到系统权限 内网学习第一天 权限提升 使用手工还是cs???msf可以不??
现在开始学习内网的相关的知识了,我们在拿下web权限过后,我们要看自己拿下的是什么权限,可能是普通的用户权限,这个连添加用户都不可以,这个时候我们就要进行权限提升操作了。 权限提升这点与我们后门进行内网渗透是乘…...
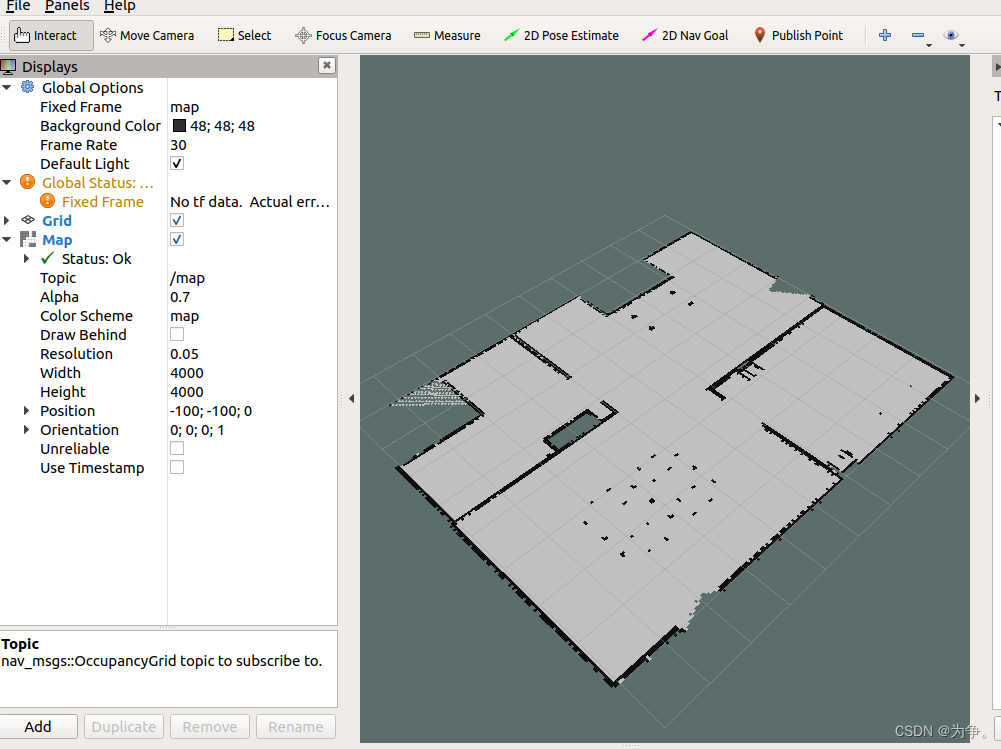
ros1仿真导航机器人 hector_mapping gmapping
仅为学习记录和一些自己的思考,不具有参考意义。 1 hector_mapping 建图过程 (1)gazebo仿真 roslaunch why_simulation why_slam.launch <launch><!-- We resume the logic in empty_world.launch, changing only the name of t…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
