【力扣 - 每日一题】3115. 质数的最大距离(一次遍历、头尾遍历、空间换时间、埃式筛、欧拉筛、打表)Golang实现
原题链接
题目描述
给你一个整数数组 nums。
返回两个(不一定不同的)质数在 nums 中 下标 的 最大距离。
示例 1:
输入: nums = [4,2,9,5,3]
输出: 3
解释: nums[1]、nums[3] 和 nums[4] 是质数。因此答案是 |4 - 1| = 3。
示例 2:
输入: nums = [4,8,2,8]
输出: 0
解释: nums[2] 是质数。因为只有一个质数,所以答案是 |2 - 2| = 0。
提示:
1 < = n u m s . l e n g t h < = 3 ∗ 1 0 5 1 <= nums.length <= 3 * 10^5 1<=nums.length<=3∗105
1 < = n u m s [ i ] < = 100 1 <= nums[i] <= 100 1<=nums[i]<=100
输入保证 nums 中至少有一个质数。
思路1:一次遍历
函数checkIsPrime用于判断num是否为质数,时间复杂度为 O ( s q r t ( n ) ) O(sqrt(n)) O(sqrt(n))
一次遍历,维护minPos表示最小的质数位置,maxPos表示最大的质数位置,最后maxPos-minPos就是答案
维护的时候,如果该数是质数,更新maxPos;如果minPos未被更新过,即minPos为初始值-1,更新minPos
整体时间复杂度 O ( N ∗ s q r t ( M ) ) O(N*sqrt(M)) O(N∗sqrt(M))
代码如下:
func checkIsPrime(num int) bool {if num <= 1 {return false}for i := 2; i*i <= num; i ++ {if num % i == 0 {return false}}return true
}
func maximumPrimeDifference(nums []int) int {minPos,maxPos := -1,-1for idx,elem := range nums {if checkIsPrime(elem) {if minPos == -1 {minPos = idx}maxPos = idx}}return maxPos - minPos
}

思路2:分别从头尾遍历
在思路1的基础上考虑对maxPos的更新过程进行优化,含义为最大的质数出现的位置,所以倒序遍历找第一个质数即可。
极端情况下,最中间的数是质数,还是会把全部的数都判断一遍。
代码:
func checkIsPrime(num int) bool {if num <= 1 {return false}for i := 2; i*i <= num; i ++ {if num % i == 0 {return false}}return true
}
func maximumPrimeDifference(nums []int) int {minPos,maxPos := -1,-1for idx,elem := range nums {if checkIsPrime(elem) {minPos = idxbreak}}for idx := len(nums) - 1; idx >= 0; idx -- {if checkIsPrime(nums[idx]) {maxPos = idx break}}return maxPos - minPos
}
思路3:标记结果 空间换时间
在思路1的基础上,考虑有的数如果重复出现的话,会被重复判断。
额外开辟map,存储该数是否为素数,空间换时间。
代码如下:
func checkIsPrime(num int) bool {if num <= 1 {return false}for i := 2; i*i <= num; i ++ {if num % i == 0 {return false}}return true
}
func maximumPrimeDifference(nums []int) int {minPos,maxPos := -1,-1mp := make(map[int]bool,len(nums))for idx,elem := range nums {if flag,ok := mp[elem]; ok {if flag {if minPos == -1 {minPos = idx}maxPos = idx}continue}if checkIsPrime(elem) {if minPos == -1 {minPos = idx}maxPos = idxmp[elem] = true}else{mp[elem] = false}}return maxPos - minPos
}
实际上并没有优化时间,很奇怪
思路4:埃式筛
可以考虑使用素数筛预处理得到所有质数,其中埃式筛的时间复杂度是 O ( n l o g l o g n ) O(nloglogn) O(nloglogn)
埃式筛优化时间复杂度的原理:
考虑这样一件事情:对于任意一个大于 1 的正整数 n,那么它的 x 倍就是合数(x > 1)。利用这个结论,我们可以避免很多次不必要的检测。
如果我们从小到大考虑每个数,然后同时把当前这个数的所有(比自己大的)倍数记为合数,那么运行结束的时候没有被标记的数就是素数了。
//埃式筛
func InitPrime(maxNum int) map[int]struct{} {mp := make(map[int]struct{},maxNum)mp[1] = struct{}{} //注意特判for i := 2; i <= maxNum; i ++ {if _,ok := mp[i]; ok { continue}for j := 2*i; j <= maxNum; j += i {mp[j] = struct{}{} //非素数}}return mp
}
func maximumPrimeDifference(nums []int) int {maxNum := 0for _,elem := range nums {if maxNum < elem {maxNum = elem}}primeMap := InitPrime(maxNum)minPos,maxPos := -1,-1for idx,elem := range nums {if _,ok := primeMap[elem];!ok {if minPos == -1 {minPos = idx}maxPos = idx}}return maxPos - minPos
}
思路5:欧拉筛
欧拉筛是在埃氏筛的基础上优化的,时间复杂度为 O ( n ) O(n) O(n)
埃氏筛法仍有优化空间,它会将一个合数重复多次标记。有没有什么办法省掉无意义的步骤呢?答案是肯定的。
如果能让每个合数都只被标记一次,那么时间复杂度就可以降到 O(n) 了。
func InitPrime(maxNum int) map[int]struct{} {mp := make(map[int]struct{},maxNum)mp[1] = struct{}{} //注意特判primes := make([]int,0,1000)for i := 2; i <= maxNum; i ++ {if _,ok := mp[i]; !ok { primes = append(primes,i)}for j := 0; primes[j] <= maxNum/i; j++ {mp[primes[j]*i] = struct{}{} //非素数if i % primes[j] == 0 {break}}}return mp
}
func maximumPrimeDifference(nums []int) int {maxNum := 0for _,elem := range nums {if maxNum < elem {maxNum = elem}}primeMap := InitPrime(maxNum)minPos,maxPos := -1,-1for idx,elem := range nums {if _,ok := primeMap[elem];!ok {if minPos == -1 {minPos = idx}maxPos = idx}}return maxPos - minPos
}
思路6: 打表
考虑到 1 < = n u m s [ i ] < = 100 1 <= nums[i] <= 100 1<=nums[i]<=100,100以内的素数个数是有限的,离线把这些数据处理出来
func checkIsPrime(num int) bool {if num <= 1 {return false}for i := 2; i*i <= num; i ++ {if num % i == 0 {return false}}return true
}
func maximumPrimeDifference(nums []int) int {minPos,maxPos := -1,-1primes := []int{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}mp := make(map[int]struct{},len(primes))for _,elem := range primes {mp[elem] = struct{}{}}numsLen := len(nums)for idx := 0; idx < numsLen; idx ++ {if _,ok := mp[nums[idx]];ok {minPos = idxbreak}}for idx := numsLen - 1; idx >= 0; idx -- {if _,ok := mp[nums[idx]];ok {maxPos = idxbreak}}return maxPos - minPos
}
相关文章:

【力扣 - 每日一题】3115. 质数的最大距离(一次遍历、头尾遍历、空间换时间、埃式筛、欧拉筛、打表)Golang实现
原题链接 题目描述 给你一个整数数组 nums。 返回两个(不一定不同的)质数在 nums 中 下标 的 最大距离。 示例 1: 输入: nums [4,2,9,5,3] 输出: 3 解释: nums[1]、nums[3] 和 nums[4] 是质数。因此答…...

【Gin】项目搭建 一
环境准备 首先确保自己电脑安装了Golang 开始项目 1、初始化项目 mkdir gin-hello; # 创建文件夹 cd gin-hello; # 需要到刚创建的文件夹里操作 go mod init goserver; # 初始化项目,项目名称:goserver go get -u github.com/gin-gonic/gin; # 下载…...

C++ 和C#的差别
首先把眼睛瞪大,然后憋住一口气,读下去: 1、CPP 就是C plus plus的缩写,中国大陆的程序员圈子中通常被读做"C加加",而西方的程序员通常读做"C plus plus",它是一种使用非常广泛的计算…...
Vue2组件传值(通信)的方式
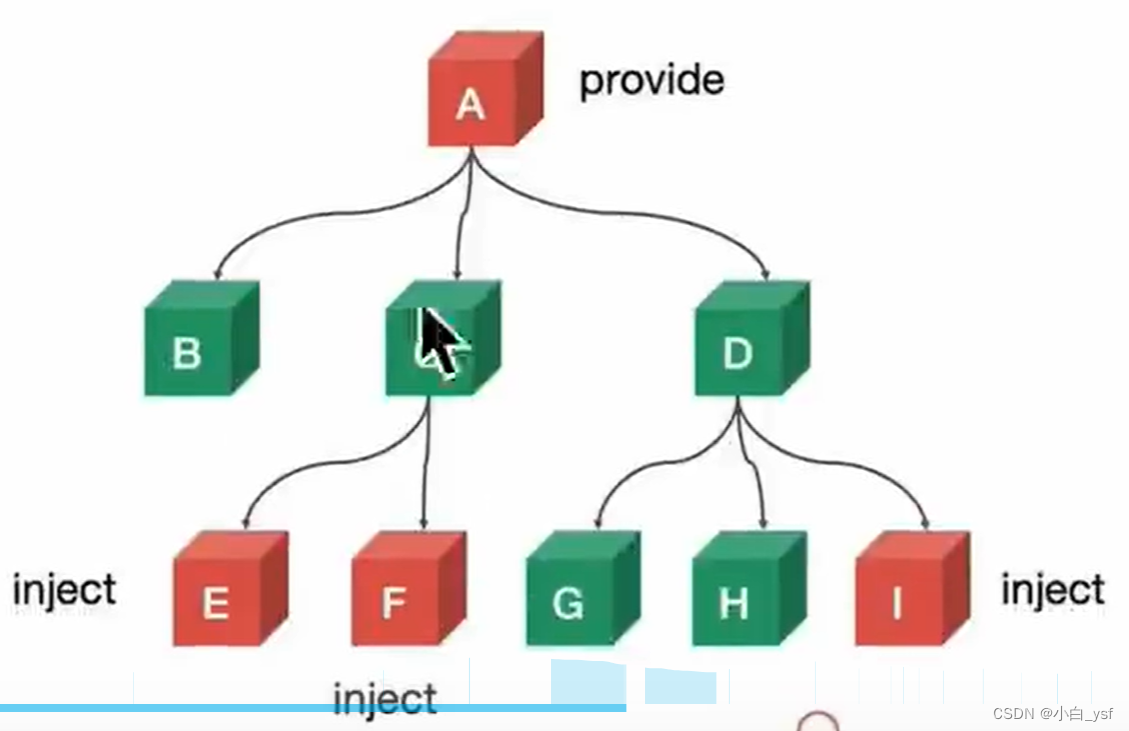
目录 1.父传后代 ( 后代拿到了父的数据 )1. 父组件引入子组件,绑定数据2. 子组件直接使用父组件的数据3. 依赖注入(使用 provide/inject API)1.在祖先组件中使用 provide2.在后代组件中使用 inject 2.后代传父 (父拿到了后代的数据)1. 子组件…...

【数据结构 - 时间复杂度和空间复杂度】
文章目录 <center>时间复杂度和空间复杂度算法的复杂度时间复杂度大O的渐进表示法常见时间复杂度计算举例 空间复杂度实例 时间复杂度和空间复杂度 算法的复杂度 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏&…...

telegram支付
今天开始接入telegram支付,参考教程这个是telegram的官方说明,详细介绍了机器人支付API。 文章公开地址 新建机器人 因为支付是一个单独的系统,所以在做支付的时候单独创建了一个bot,没有用之前的bot了,特意这样将其分开。创建bot的方法和之前不变,这里不过多介绍。 获…...

elasticsearch-6.8.23的集群搭建过程
三个节点的 ElasticSearch 集群搭建步骤 准备三台机器:28.104.87.98、28.104.87.100、28.104.87.101 和 ElasticSearch 的安装包 elasticsearch-6.8.23.tar.gz ----------------------------- 28.104.87.98,使用 root 用户操作 ----------------------…...

javascript输出语法
javascript输出有三种方式 一种是弹窗输出,就是网页弹出一个对话框,弹出输出内容 语法是aler(内容) 示例代码如下 <body> <script> alert(你好); </script> </body> 这段代码运行后网页会出现一个对话框,弹出你…...
仓库管理系统26--权限设置
原创不易,打字不易,截图不易,多多点赞,送人玫瑰,留有余香,财务自由明日实现 1、权限概述 在应用软件中,通常将软件的功能分为若干个子程序,通过主程序调用。那么,通过…...

d3dx9_43.dll丢失怎么解决?d3dx9_43.dll怎么安装详细教程
在使用计算机中,如果遇到d3dx9_43.dll丢失或许找不到d3dx9_43.dll无法运行打开软件怎么办?这个是非常常见问题,下面我详细介绍一下d3dx9_43.dll是什么文件与d3dx9_43.dll的各种问题以及d3dx9_43.dll丢失的多个解决方法! 一、d3dx9…...
)
[C++] 退出清理函数解读(exit、_exit、abort、atexit)
说明:在C中,exit、_exit(或_Exit)、abort和atexit是用于控制程序退出和清理的标准库函数。下面是对这些函数的详细解读: exit 函数原型:void exit(int status);作用:exit函数用于正常退出程序…...
)
代码随想录(回溯)
组合(Leetcode77) 思路 用递归每次遍历从1-n得数,然后list来记录是不是组合到k个了,然后这个每次for循环的开始不能和上一个值的开始重复,所以设置个遍历开始索引startindex class Solution {static List<List<…...

编译原理1
NFA&DFA 在正规式的等价证明可以借助正规集,也可以通过有限自动机DFA来证明等价,以下例题是针对DFA证明正规式的等价,主要步骤是①NFA;②状态转换表; ③状态转换矩阵; ④化简DFA; 文法和语…...

【信息系统项目管理师知识点速记】组织通用管理:流程管理
23.2 流程管理 通过流程视角能够真正看清楚组织系统的本质与内在联系,理顺流程能够理顺整个组织系统。流程是组织运行体系的框架基础,流程框架的质量影响和决定了整个组织运行体系的质量。把流程作为组织运行体系的主线,配备满足流程运作需要的资源,并构建与流程框架相匹配…...

前端 JS 经典:箭头函数的意义
箭头函数是为了消除函数的二义性。 1. 二义性 函数的二义性指函数有不同的两种用法,就造成了二义性,函数的两种用法:1. 指令序列。2. 构造器 1.1 指令序列 就是调用函数,相当于将函数内部的代码再从头执行一次。 1.2 构造器 …...

Java List操作详解及常用方法
Java List操作详解及常用方法 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 什么是Java List? Java中的List是一种动态数组,它允许存…...
《mysql篇》--查询(进阶)
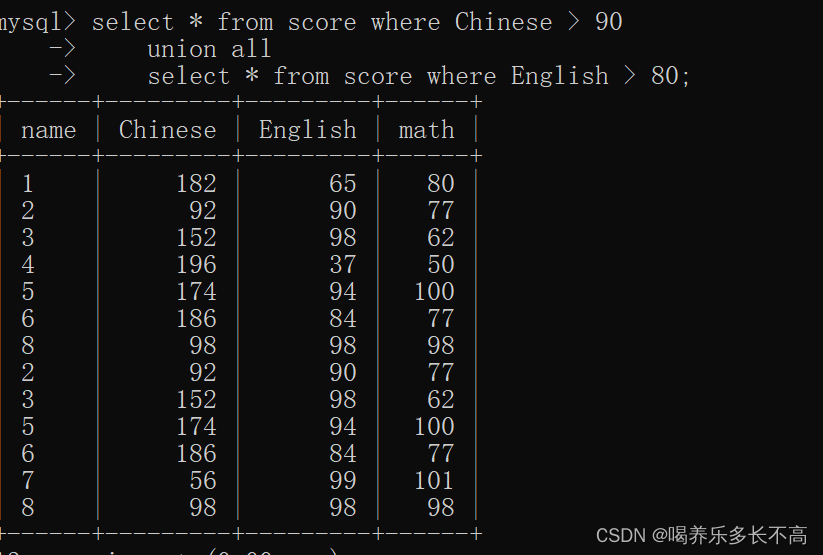
目录 将查询结果作为插入数据 聚合查询 聚合函数 count sum group by子句 having 联合查询 笛卡尔积 多表查询 join..on实现多表查询 内连接 外连接 自连接 子查询 合并查询 将查询结果作为插入数据 Insert into 表2 select * from 表1//将表1的查询数据插入…...

数据库-MySQL 实战项目——书店图书进销存管理系统数据库设计与实现(附源码)
一、前言 该项目非常适合MySQL入门学习的小伙伴,博主提供了源码、数据和一些查询语句,供大家学习和参考,代码和表设计有什么不恰当还请各位大佬多多指点。 所需环境 MySQL可视化工具:navicat; 数据库:MySq…...
eNSP中WLAN的配置和使用
一、基础配置 1.拓扑图 2.VLAN和IP配置 a.R1 <Huawei>system-view [Huawei]sysname R1 GigabitEthernet 0/0/0 [R1-GigabitEthernet0/0/0]ip address 200.200.200.200 24 b.S1 <Huawei>system-view [Huawei]sysname S1 [S1]vlan 100 [S1-vlan100]vlan 1…...
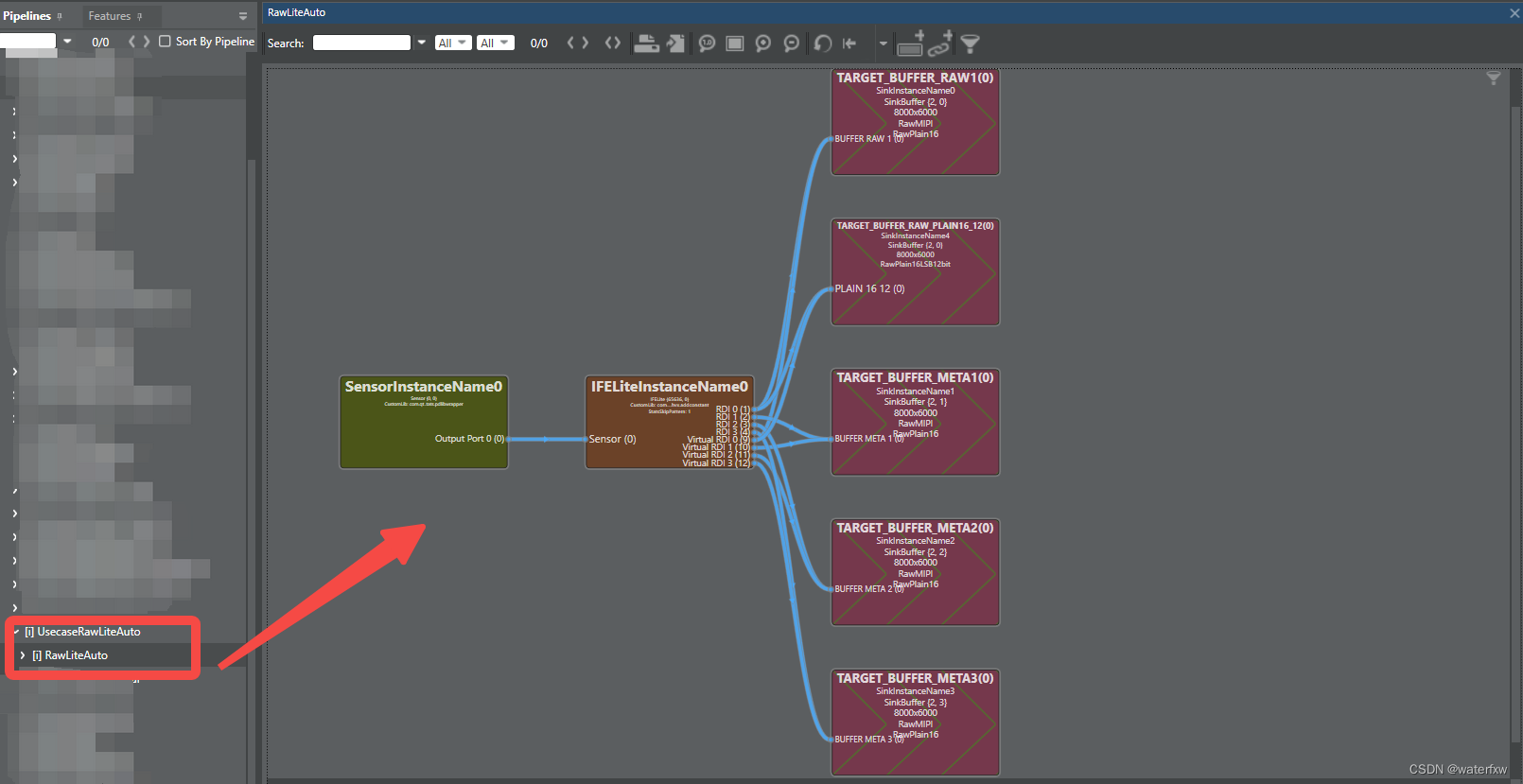
<sa8650>QCX ID16_UsecaseRawLiteAuto 使用详解
<sa8650>QCX ID16_UsecaseRawLiteAuto 使用详解 一、前言二、ID16_UsecaseRawLiteAuto拓扑图三、UsecaseRawLiteAuto拓扑图 解析3.1 camxUsecaseRawLiteAuto.xml3.2 camxRawLiteAuto.xml四、测试一、前言 我们在使用QCX时,如果由于使用的摄像头自带了ISP,那么可能不需要使…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
