LeetCode 106 从中序与后序遍历序列构造二叉树
根据中序遍历和后序遍历的性质,还原二叉树,详细见注释
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//空,直接返回nullif(inorder.size() == 0) return nullptr;//一个,返回一个node结点if(inorder.size() == 1) return new TreeNode(inorder[0]);int size = postorder.size();int val = postorder[size-1];//后续遍历的最后一个元素是根节点TreeNode* root = new TreeNode(val);//在中序中找到根节点的位置auto idx1 = find(inorder.begin(), inorder.end(), val);//中序遍历中根节点的位置左侧是左子树中序遍历,右侧为右子树中序遍历//分别拷贝构造出新的中序遍历vectorvector<int> inorder_left(inorder.begin(), idx1);vector<int> inorder_right(idx1+1, inorder.end());int left_num = inorder_left.size();//后序遍历左子树等于后序遍历起点+中序遍历左子树vector.size()vector<int> postorder_left(postorder.begin(), postorder.begin()+left_num);//后边遍历右子树等于后序遍历左子树下一个元素到倒数第二个元素vector<int> postorder_right(postorder.begin()+left_num, postorder.end()-1);//构造左右子树root->left = buildTree(inorder_left, postorder_left);root->right = buildTree(inorder_right, postorder_right);return root;}相关文章:

LeetCode 106 从中序与后序遍历序列构造二叉树
根据中序遍历和后序遍历的性质,还原二叉树,详细见注释 TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//空,直接返回nullif(inorder.size() 0) return nullptr;//一个,返回一个nod…...

Vue Router的深度解析
引言 在现代Web应用开发中,客户端路由已成为实现流畅用户体验的关键技术。与传统的服务器端路由不同,客户端路由通过JavaScript在浏览器中控制页面内容的更新,避免了页面的全量刷新。Vue Router作为Vue.js官方的路由解决方案,以其…...
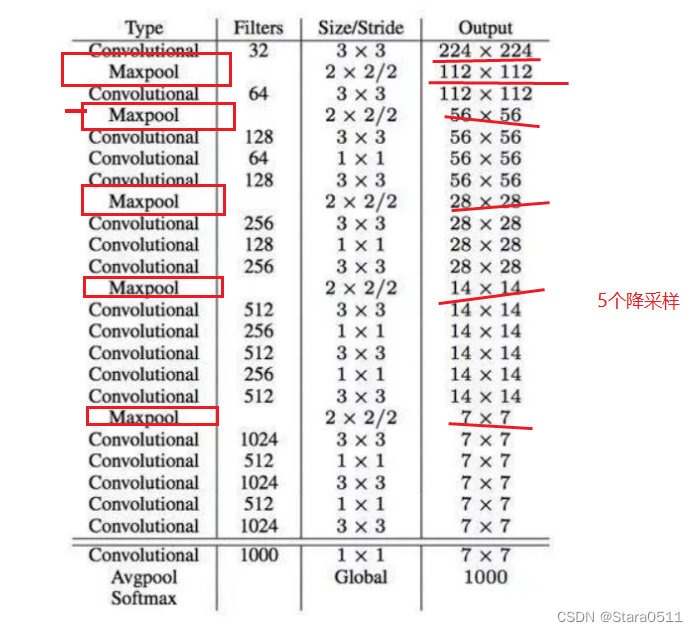
YOLO-V2
一、V2版本细节升级 1、YOLO-V2: 更快!更强 1.1 做的改进内容 1. YOLO-V2-Batch Normalization V2版本舍弃Dropout,卷积后每一层全部加入Batch Normalization网络的每一层的输入都做了归一化,收敛相对更容易经过Batch Norma…...
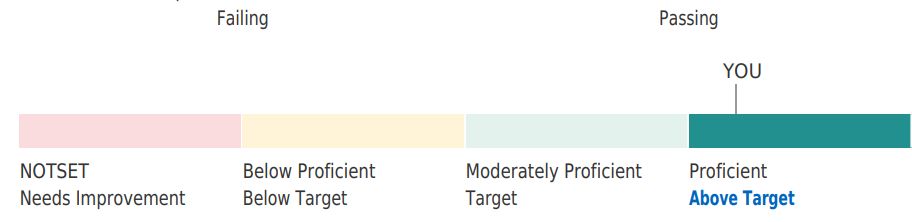
pmp考试的通过标准是什么?
PMP考试的是否通过并不是依据类似其他考试的数值成绩,是通过考生收到邮件通知后去主动查询具体的页面得知的。查询页除了电子证书的下载方式,还有成绩报告单的选项以及成绩饼状图,具体如下: 页面中显示“PASS”表示考试通过。 显…...
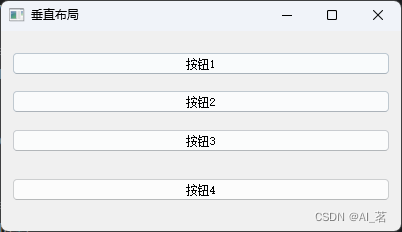
不懂PyQt5垂直布局?只需3分钟即可学会
PyQt5中实现垂直布局,主要使用QVBoxLayout类。该布局管理器将子控件垂直排列,并可以根据需要自动调整大小。使用QVBoxLayout可以方便地构建从上到下排列的界面元素。 import sys from PyQt5.QtWidgets import QApplication, QVBoxLayout, QWidget, QPus…...

从零开始实现大语言模型(二):文本数据处理
1. 前言 神经网络不能直接处理自然语言文本,文本数据处理的核心是做tokenization,将自然语言文本分割成一系列tokens。 本文介绍tokenization的基本原理,OpenAI的GPT系列大语言模型使用的tokenization方法——字节对编码(BPE, byte pair en…...

生物分子生物学实验过程的自动化与智能监控系统设计
开题报告:生物分子生物学实验过程的自动化与智能监控系统设计 一、引言 随着生物科学技术的飞速发展,生物分子生物学实验在科研、医疗、农业等领域的应用日益广泛。然而,传统的生物分子生物学实验过程大多依赖于人工操作,存在操…...

linux的shell脚本编程详解
Shell 脚本是一种用于自动化任务的脚本语言,在 Linux 和其他类 Unix 操作系统中非常流行。它通常用于任务自动化、系统管理和批处理。编写 Shell 脚本并使其自动化编译过程(例如使用 gcc 编译 C/C 程序)是一种常见的任务。 以下是一个详细的…...

Redis 7.x 系列【11】数据类型之位图(Bitmap)
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 概述2. 基本命令2.1 SETBIT2.2 GETBIT2.3 BITCOUNT2.4 BITPOS2.5 BITFIELD2.6 BITF…...

如何评定旅游卡的品质与服务?
评定旅游卡的品质与服务,可以从以下几个关键方面进行综合考量: 公司实力与资质:选择有实力、资质齐全的公司发行的旅游卡。查看公司背景,确认其是否长期稳定运营,是否具有旅游行业的专业资质,如旅行社许可证…...

适合学生暑假适用的护眼大路灯有哪些?五款好用护眼灯分享!
在护眼领域,护眼大路灯已经成为越来越多人的选择。这种具备实力的工具可以有效地缓解用眼疲劳、改善光线环境,是学生党和办公族的必备神器。然而,市面上的护眼大路灯品牌众多,如何选择一款性价比高、品质优良的产品呢?…...

linux服务器 部署jenkins
在 Linux 服务器上部署 Jenkins 通常包括以下几个步骤: 更新系统软件包: sudo apt update sudo apt upgrade 安装 Java: Jenkins 需要 Java 运行时环境。推荐使用 OpenJDK 11。 sudo apt install openjdk-11-jdk 添加 Jenkins 软件源并导入…...

电商控价:系统监测的必要性与优势
在品牌的发展进程中,会遭遇各种各样的渠道问题,控价乃是其中颇为关键的一环。品牌进行控价的目的无疑是为了妥善治理低价链接,低价链接的发现途径可以是人工,也可以是系统。力维网络在为上百个品牌提供服务的过程中察觉到…...

港股下半年能恢复上涨趋势吗?
今日港股两大指数涨跌不一,早盘盘初恒指冲高,涨幅一度扩大至1%。截至收盘,香港恒生指数涨0.57%。板块方面,电力、航空、石油、内险股、燃料电池、环保等板块涨幅居前;互动媒体与服务、生物科技、汽车零部件、新经济概念…...

软件测试项目实战:银行贷款业务测试介绍-2
1、利息计算 正常利息贷款本金*借款天数*贷款年利率/360 罚息逾期本金*逾期天数*逾期年利率/360 复利逾期利息*逾期天数*逾期年利率/360 2、贷款五级分类 正常贷款:正常及逾期60天以内 关注贷款:逾期60天及以上,不足90天 次级贷款࿱…...

如何将Hive表的分区字段插入PG表对应的时间戳字段?
文章目录 1、背景描述2、场景分析 1、背景描述 数据仓库的建设通常是为业务和决策服务的。在数仓开发的应用层阶段,BI可以直接从主题层/业务层取数,而前端需要根据具体的作图需求通过后端查询数据库 作图的指标需要根据主题层/业务层做查询计算…...

Spring Boot与MyBatis的集成应用
Spring Boot与MyBatis的集成应用 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来聊聊Spring Boot与MyBatis的集成应用。MyBatis是一款优秀的持久层框…...
在昇腾服务器上使用llama-factory对baichuan2-13b模型进行lora微调
什么是lora微调 LoRA 提出在预训练模型的参数矩阵上添加低秩分解矩阵来近似每层的参数更新,从而减少适配下游任务所需要训练的参数。 环境准备 这次使用到的微调框架是llama-factory。这个框架集成了对多种模型进行各种训练的代码,少量修改就可使用。 …...

Kafka 管理TCP连接
生产者管理TCP连接 Kafka生产者程序概览 Kafka的Java生产者API主要的对象就是KafkaProducer。通常我们开发一个生产者的步骤有4步: 第1步:构造生产者对象所需的参数对象。 第2步:利用第1步的参数对象,创建KafkaProducer对象实例…...
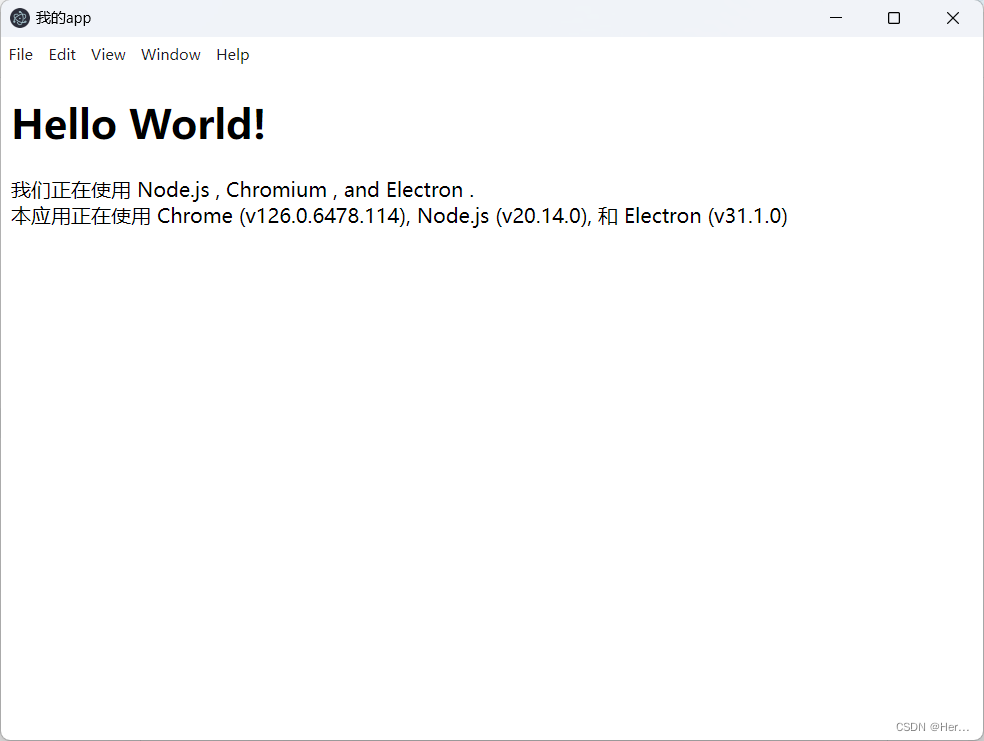
electron教程(一)创建项目
一、方式① 根据官网描述将electron/electron-quick-start项目克隆下来并启动 electron/electron-quick-start地址: GitHub - electron/electron-quick-start: Clone to try a simple Electron app git clone https://github.com/electron/electron-quick-start…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
