双向广搜——AcWing 190. 字串变换
双向广搜
定义
双向广度优先搜索(Bi-directional Breadth-First Search, Bi-BFS)是一种在图或树中寻找两点间最短路径的算法。与传统的单向广度优先搜索相比,它从起始点和目标点同时开始搜索,从而有可能显著减少搜索空间,提高搜索效率,特别是在处理大规模图或者寻找最短路径时更为明显。
运用情况
- 最短路径问题:当需要快速找到两个节点间的最短路径时,特别是路径非常长或者图非常大的情况下,双向BFS比单向BFS更高效。
- 有界搜索问题:在一些问题中,比如迷宫求解,我们知道起始点和终点,且关心的是尽快相遇而不是探索整个图,这时双向BFS非常适用。
- 游戏AI:在某些游戏中,为了快速计算玩家与目标之间的最短路径,可以使用双向BFS。
- 网络路由:在网络通信中寻找最短的路由路径时,也可以应用此算法。
注意事项
- 相遇判断:当两个搜索的前沿相遇时,需要确保正确识别并停止搜索,避免重复计算。
- 路径合并:找到相遇点后,需要合并两个方向的路径以得到完整的最短路径。
- 空间复杂度:虽然可以减少搜索的深度,但同时维护两个队列(或集合)可能会增加额外的空间消耗。
- 平衡问题:为了优化性能,需要尽量保持两个方向的搜索速度平衡,可以通过调整每一步扩展的节点数来实现。
解题思路
- 初始化:设置两个队列,一个用于存储从起点出发的节点,另一个用于存储从终点出发的节点。同时,为两个方向的节点分别标记已访问状态,防止重复访问。
- 广度优先遍历:同时进行两个方向的广度优先遍历。每次遍历时,从两个队列中各取出一层的节点进行扩展,并将新扩展的节点加入到相应的队列中。
- 检查相遇:在扩展节点的过程中,检查是否有节点已经被另一个方向访问过。如果发现这样的节点,说明找到了一条从起点到终点的路径,此时停止搜索。
- 路径合并:从相遇节点开始,逆向追踪标记,直到回到起点或终点,这样就可以得到完整的最短路径。
- 优化策略:根据具体问题,可能需要考虑启发式信息、队列管理策略等进一步优化搜索过程。
AcWing 190. 字串变换
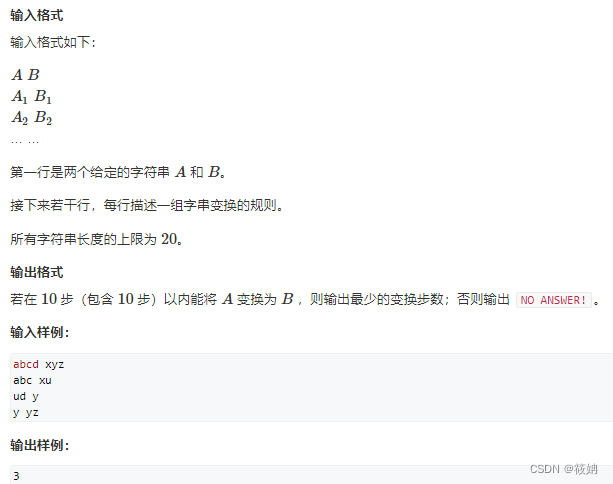
题目描述
190. 字串变换 - AcWing题库

运行代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>using namespace std;const int N = 6;int n;
string A, B;
string a[N], b[N];int extend(queue<string>& q, unordered_map<string, int>&da, unordered_map<string, int>& db, string a[N], string b[N])
{int d = da[q.front()];while (q.size() && da[q.front()] == d){auto t = q.front();q.pop();for (int i = 0; i < n; i ++ )for (int j = 0; j < t.size(); j ++ )if (t.substr(j, a[i].size()) == a[i]){string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size());if (db.count(r)) return da[t] + db[r] + 1;if (da.count(r)) continue;da[r] = da[t] + 1;q.push(r);}}return 11;
}int bfs()
{if (A == B) return 0;queue<string> qa, qb;unordered_map<string, int> da, db;qa.push(A), qb.push(B);da[A] = db[B] = 0;int step = 0;while (qa.size() && qb.size()){int t;if (qa.size() < qb.size()) t = extend(qa, da, db, a, b);else t = extend(qb, db, da, b, a);if (t <= 10) return t;if ( ++ step == 10) return -1;}return -1;
}int main()
{cin >> A >> B;while (cin >> a[n] >> b[n]) n ++ ;int t = bfs();if (t == -1) puts("NO ANSWER!");else cout << t << endl;return 0;
}
代码思路
-
输入处理:首先读取起始字符串A和目标字符串B,然后逐行读取变换规则(子串A[i]到B[i]的变换)直到文件结束。
-
双端BFS:算法采用了双端BFS策略,即同时从字符串A和B出发,试图找到两者之间的最短变换路径。使用两个队列
qa和qb分别存储从A和B出发的可能状态,以及两个哈希表da和db记录每个状态到起点的距离。 -
扩展函数:定义了
extend函数,用于从一个队列中取出所有状态并尝试应用所有变换规则,扩展出新的状态加入队列,并更新距离哈希表。这个函数是BFS的关键,它确保每次扩展只增加一步操作。 -
主循环:在主循环中交替从两端扩展,直到找到变换路径或者达到最大步数限制。
-
结果判断:最后,根据搜索结果输出最少步数或"No Answer!"。
改进思路
-
减少重复计算:当前代码在扩展状态时,对每个状态与每条规则都进行了匹配尝试,这可能会导致大量重复计算,尤其是在规则较多或字符串较长时。可以通过维护一个已访问状态的集合来避免重复探索相同的状态。
-
规则预处理:为了提高效率,可以在开始搜索之前对变换规则进行预处理,比如建立一个从子串到新子串的直接映射,这样在扩展状态时可以直接查找而无需遍历所有规则。
-
剪枝:在双向BFS中,当从两端搜索的边界状态的距离之和已经大于当前最小步数时,可以提前终止搜索,这是一种有效的剪枝策略。
-
内存使用优化:考虑使用更节省空间的数据结构,比如使用滚动数组或者动态调整容器大小来减少内存占用。
相关文章:

双向广搜——AcWing 190. 字串变换
双向广搜 定义 双向广度优先搜索(Bi-directional Breadth-First Search, Bi-BFS)是一种在图或树中寻找两点间最短路径的算法。与传统的单向广度优先搜索相比,它从起始点和目标点同时开始搜索,从而有可能显著减少搜索空间&#x…...

工商业光伏项目如何快速开发?
一、前期调研与规划 1、屋顶资源评估:详细测量屋顶面积、承重能力及朝向,利用光伏业务管理软件进行日照分析和发电量预测,确保项目可行性。 2、政策与补贴研究:深入了解当地政府对工商业光伏项目的政策支持和补贴情况࿰…...
Kafka入门-分区及压缩
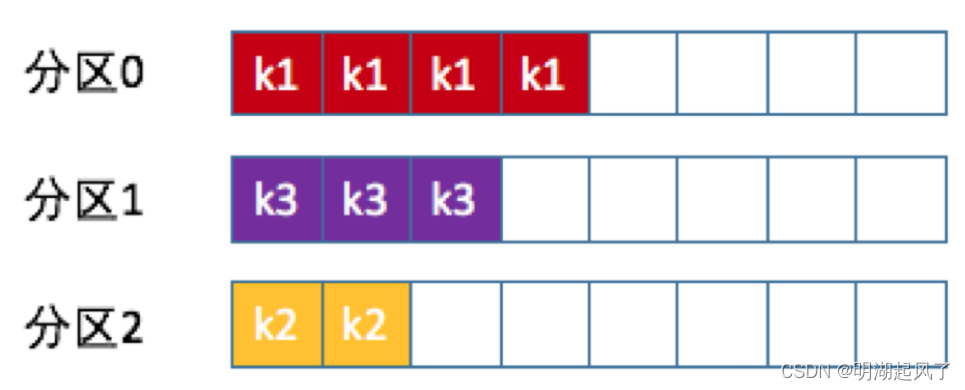
一、生产者消息分区 Kafka的消息组织方式实际上是三级结构:主题-分区-消息。主题下的每条消息只会保存在某一个分区中,而不会在多个分区中被保存多份。 分区的作用就是提供负载均衡的能力,或者说对数据进行分区的主要原因,就是为…...

被⽹络罪犯利⽤的5⼤ChatGPT越狱提⽰
⾃ChatGPT发布的近18个月以来,⽹络罪犯们已经能够利⽤⽣成式AI进⾏攻击。OpenAI在其内容政策中制定了限制措施,以阻⽌⽣成恶意内容。作为回应,攻击者们创建了⾃⼰的⽣成式AI平台,如 WormGPT和FraudGPT,并且他们还分享了…...
AVR晶体管测试仪开源制作与验证
AVR晶体管测试仪开源制作与验证 📍原项目地址:https://www.mikrocontroller.net/articles/AVR_Transistortester github地址:https://github.com/Mikrocontroller-net/transistortester 🎈EasyEDA项目地址:https://osh…...

头条系统-05-延迟队列精准发布文章-概述添加任务(db和redis实现延迟任务)、取消拉取任务定时刷新(redis管道、分布式锁setNx)...
文章目录 延迟任务精准发布文章 1)文章定时发布2)延迟任务概述 2.1)什么是延迟任务2.2)技术对比 2.2.1)DelayQueue2.2.2)RabbitMQ实现延迟任务2.2.3)redis实现 3)redis实现延迟任务4)延迟任务服务实现 4.1)搭建heima-leadnews-schedule模块4.2)数据库准备4.3)安装redis4.4)项目…...

不同系统间数据交换要通过 api 不能直接数据库访问
很多大数据开发提供数据给外部系统直接给表结构,这是不好的方式。在不同系统间进行数据交换时,通过API(应用程序编程接口)而非直接访问数据库是现代系统集成的一种最佳实践。 目录 为什么要通过API进行数据交换如何通过API进行数据…...
深度探索“目录名称无效“:原因、解决方案与最佳实践
目录名称无效:现象背后的秘密 在日常使用电脑或移动设备时,我们时常会遇到“目录名称无效”的错误提示,这一提示仿佛是一道无形的屏障,阻断了我们与重要数据的联系。从本质上讲,“目录名称无效”意味着系统无法识别或…...

open3d基础使用-简单易懂
Open3D是一个开源库,主要用于快速开发处理3D数据的软件。它提供了丰富的数据结构和算法,支持点云、网格和RGB-D图像等多种3D数据的处理。以下是对Open3D基础使用的详细归纳和说明: 一、安装Open3D Open3D可以通过Python的包管理器pip进行安…...

【前端】HTML+CSS复习记录【5】
文章目录 前言一、padding、margin、border(边框边距)二、样式优先级三、var(使用 CSS 变量更改多个元素样式)四、media quary(媒体查询)系列文章目录 前言 长时间未使用HTML编程,前端知识感觉…...

三分钟看懂SMD封装与COB封装的差异
全彩LED显示屏领域中,COB封装于SMD封装是比较常见的两种封装方式,SMD封装产品主要有常规小间距以及室内、户外型产品,COB封装产品主要集中在小间距以及微间距系列产品中,今天跟随COB显示屏厂家中品瑞一起快速看懂SMD封装与COB封装…...
深入理解策略梯度算法
策略梯度(Policy Gradient)算法是强化学习中的一种重要方法,通过优化策略以获得最大回报。本文将详细介绍策略梯度算法的基本原理,推导其数学公式,并提供具体的例子来指导其实现。 策略梯度算法的基本概念 在强化学习…...

Unicode 和 UTF-8 以及它们之间的关系
通俗易懂的 Unicode 和 UTF-8 解释 Unicode 是什么? 想象一下,我们有一个巨大的图书馆,这个图书馆里有各种各样的书,每本书都有一个唯一的编号。Unicode 就像是这个图书馆的目录系统,它给世界上所有的字符࿰…...

【C++】多态详解
💗个人主页💗 ⭐个人专栏——C学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 一、多态概念 二、多态的定义及实现 1. 多态的构成条件 2. 虚函数 2.1 什么是虚函数 2.2 虚函数的重写 2.3 虚函数重写的两个…...

C#异常捕获
前言 在C#中,我们无法保证我们编写的程序没有一点bug,如果我们对于这些抛出异常的bug不进行任何的处理的话,那么我们的软件在抛出这些异常的时候就会崩溃,也就是软件闪退,并且这种闪退由于我们没有进行处理࿰…...

工业一体机根据软件应用需求灵活选配
在当今工业领域,数字化、智能化的发展趋势愈发明显,工业一体机作为关键的设备,其重要性日益凸显。而能够根据软件应用需求进行灵活选配的工业一体机,更是为企业提供了高效、定制化的解决方案。 一、工业一体机的全封闭无风扇散热功…...
centos7 mqtt服务mosquitto搭建记录
1、系统centos7.6,安装默认版本 yum install mosquitto 2、启动运行 systemctl start mosquitto 3、设置自启动 systemctl enable mosquitto 4、修改配置文件 vim /etc/mosquitto/mosquitto.conf 监听端口,默认为1883,需要修改删除前面…...

双阶段目标检测算法:精确与效率的博弈
双阶段目标检测算法:精确与效率的博弈 目标检测是计算机视觉领域的一个核心任务,它涉及在图像或视频中识别和定位多个对象。双阶段目标检测算法是一种特殊的目标检测方法,它通过两个阶段来提高检测的准确性。本文将详细介绍双阶段目标检测算…...

Python量化交易策略
策略详情 按照1分k线图;跳过9:30点1分k线图不计算 买入;监控市面的可转债;当某1分涨幅大于x涨幅,一直重复x次,选择买入,符合x设置的条件只选择成交额最大的可转债买入(x要自定义&…...
为什么我感觉 C 语言在 Linux 下执行效率比 Windows 快得多?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「Linux的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!!Windows的终端或者叫控制台…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
