力扣404周赛 T1/T2/T3 枚举/动态规划/数组/模拟
- 博客主页:誓则盟约
- 系列专栏:IT竞赛 专栏
- 关注博主,后期持续更新系列文章
- 如果有错误感谢请大家批评指出,及时修改
- 感谢大家点赞👍收藏⭐评论✍



3200.三角形的最大高度【简单】
题目:
给你两个整数 red 和 blue,分别表示红色球和蓝色球的数量。你需要使用这些球来组成一个三角形,满足第 1 行有 1 个球,第 2 行有 2 个球,第 3 行有 3 个球,依此类推。
每一行的球必须是 相同 颜色,且相邻行的颜色必须 不同。
返回可以实现的三角形的 最大 高度。
示例 1:
输入: red = 2, blue = 4
输出: 3
解释:
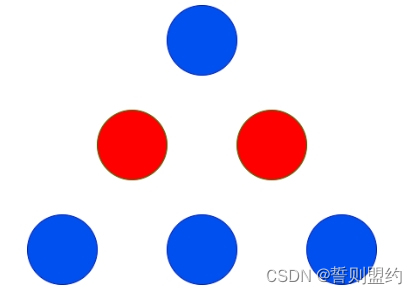
上图显示了唯一可能的排列方式。
示例 2:
输入: red = 2, blue = 1
输出: 2
解释:
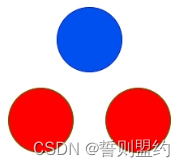
上图显示了唯一可能的排列方式。
示例 3:
输入: red = 1, blue = 1
输出: 1
示例 4:
输入: red = 10, blue = 1
输出: 2
解释:
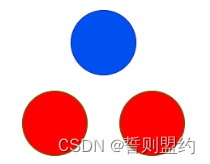
上图显示了唯一可能的排列方式。
提示:
1 <= red, blue <= 100
分析问题:
这里需要分情况讨论:
- 奇排是蓝球:那么蓝色第一层初始值为1,往下每层个数依次+2,需要蓝色球的个数每次都加本层的个数。模拟过程,求出蓝色球的数量一共够放多少层。同样的办法求出红色球能放的总层数。两者去min值*2就是初定的层数,但是需要注意的是,这里当蓝色球层数大于红色球层数时,总层数是需要+1的,因为蓝球开始又以蓝球结束。总层数+1即为结果。
- 奇排是红球:同样的道理,设红球的初始值为1,求出层数即可。
最后返回二者的max值即为答案。
这道题容易产生一种错误的思路:数量多的球就应该放第一排,或者数量少的球就应该放第一排。这种思路是错的,可以自行验证。
代码实现:
class Solution:def maxHeightOfTriangle(self, red: int, blue: int) -> int:b,r=1,0h1,h2=1,0s1,s2=1,0while s1+h1+2<=blue:h1+=2b+=1s1+=h1while s2+h2+2<=red:h2+=2r+=1s2+=h2a=min(b,r)*2if b-r>=1: a+=1r,b=1,0h1,h2=1,0s1,s2=1,0while s1+h1+2<=red:h1+=2r+=1s1+=h1while s2+(h2+2)<=blue:h2+=2b+=1s2+=h2k=min(b,r)*2if r-b>=1: k+=1return max(a,k)
3201.找出有效子序列的最大长度I【中等】
题目:
给你一个整数数组 nums。
nums 的子序列 sub 的长度为 x ,如果其满足以下条件,则称其为 有效子序列:
(sub[0] + sub[1]) % 2 == (sub[1] + sub[2]) % 2 == ... == (sub[x - 2] + sub[x - 1]) % 2
返回 nums 的 最长的有效子序列 的长度。
一个 子序列 指的是从原数组中删除一些元素(也可以不删除任何元素),剩余元素保持原来顺序组成的新数组。
示例 1:
输入: nums = [1,2,3,4]
输出: 4
解释:
最长的有效子序列是 [1, 2, 3, 4]。
示例 2:
输入: nums = [1,2,1,1,2,1,2]
输出: 6
解释:
最长的有效子序列是 [1, 2, 1, 2, 1, 2]。
示例 3:
输入: nums = [1,3]
输出: 2
解释:
最长的有效子序列是 [1, 3]。
提示:
2 <= nums.length <= 2 * 10**51 <= nums[i] <= 10**7
分析问题:
这个题是下面3202题的一种简单的情况,直接看下面一题的题解。
代码实现:
class Solution:def maximumLength(self, nums: List[int]) -> int:k=2f = [[0]*k for i in range(k)]for x in nums:x%=kfor y in range(k):f[y][x]=f[x][y]+1return max(map(max,f)) 
3202.找出有效子序列的最大长度II【中等】
题目:
给你一个整数数组 nums 和一个 正 整数 k 。
nums 的一个
子序列
sub 的长度为 x ,如果其满足以下条件,则称其为 有效子序列 :
(sub[0] + sub[1]) % k == (sub[1] + sub[2]) % k == ... == (sub[x - 2] + sub[x - 1]) % k
返回 nums 的 最长有效子序列 的长度。
示例 1:
输入:nums = [1,2,3,4,5], k = 2
输出:5
解释:
最长有效子序列是 [1, 2, 3, 4, 5] 。
示例 2:
输入:nums = [1,4,2,3,1,4], k = 3
输出:4
解释:
最长有效子序列是 [1, 4, 1, 4] 。
提示:
2 <= nums.length <= 10**31 <= nums[i] <= 10**71 <= k <= 10**3
分析问题:
这里的T3和T2是一个道理,只不过这里的k值可以是任意一个值。分析问题,看透问题的本质。其实这道题给的数组的原本的值并没用,我们需要的是他们各自对k取模之后的值,因为我们要比较的是他们的余数[0,k-1];
对他们各自取模后,可以发现有效子序列的前两个值和后面第三个第四个值就是一个以2为周期的长度为2的数组。也就是说整个有效子序列里面奇数项是同一个数,偶数项是同一个数。奇数项还有可能等于偶数项。
那么知道了这一点,我们用x遍历原数组nums,用y遍历0-k-1就可以可以得到一个递推关系式:f[y][x]=f[x][y]+1,因为以 3 2 结尾的话前面一个数一定是2,那么意思就是说 3 前面是以2 3 结尾的。所以f[3][2]=f[2][3]+1。
代码实现:
class Solution:def maximumLength(self, nums: List[int],k:int) -> int:f = [[0]*k for i in range(k)]for x in nums:x%=kfor y in range(k):f[y][x]=f[x][y]+1return max(map(max,f))
总结:
T3代码详解:
- 创建了一个二维列表
f,大小为kxk,并初始化为全0。 - 遍历
nums列表中的每个元素x,将其对k取模的结果作为新的x。 - 然后遍历
k个值作为y,将f[y][x]的值设置为f[x][y] + 1。 - 最后,使用
max(map(max, f))找出f中所有子列表中的最大值中的最大值,并将其作为结果返回。
考点:
- 对列表的操作和遍历。
- 二维列表的创建和使用。
map()函数和max()函数的应用。
收获:
- 加深了对列表操作和遍历的理解,包括如何创建和修改二维列表。
- 熟悉了
map()函数和max()函数的结合使用,以找出复杂数据结构中的最大值。 - 提高了通过代码解决数学问题的能力,例如通过取模运算和二维列表来处理数据之间的关系。

“前进!前进!!不择手段地前进!!!”——《三体:死神永生》
相关文章:

力扣404周赛 T1/T2/T3 枚举/动态规划/数组/模拟
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 3200.三角形的最大高度【简单】 题目: 给你两个整数 red 和 b…...

Taurus 性能测试工具详解
文章目录 简介原理安装编写测试配置运行测试集成其他工具结果分析优点与缺点优点缺点 参考资料总结 简介 Taurus 是一个开源的自动化测试工具,用于简化和增强性能测试流程。与其他性能测试工具不同,Taurus 旨在通过友好的 YAML 配置文件和对多种负载测试…...
)
天猫商品详情API接口(店铺|标题|主图|价格|SKU属性等)
天猫商品详情API接口为开发者提供了获取天猫商品详细信息的能力,包括店铺信息、商品标题、主图、价格、SKU属性等。以下是该接口的使用过程和相关技术要点: 注册账号并创建应用 注册账号:需要在天猫开放平台注册一个开发者账号。创建应用&a…...
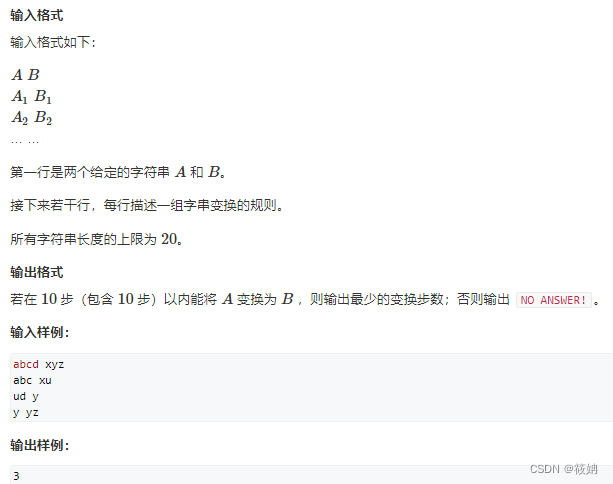
双向广搜——AcWing 190. 字串变换
双向广搜 定义 双向广度优先搜索(Bi-directional Breadth-First Search, Bi-BFS)是一种在图或树中寻找两点间最短路径的算法。与传统的单向广度优先搜索相比,它从起始点和目标点同时开始搜索,从而有可能显著减少搜索空间&#x…...

工商业光伏项目如何快速开发?
一、前期调研与规划 1、屋顶资源评估:详细测量屋顶面积、承重能力及朝向,利用光伏业务管理软件进行日照分析和发电量预测,确保项目可行性。 2、政策与补贴研究:深入了解当地政府对工商业光伏项目的政策支持和补贴情况࿰…...
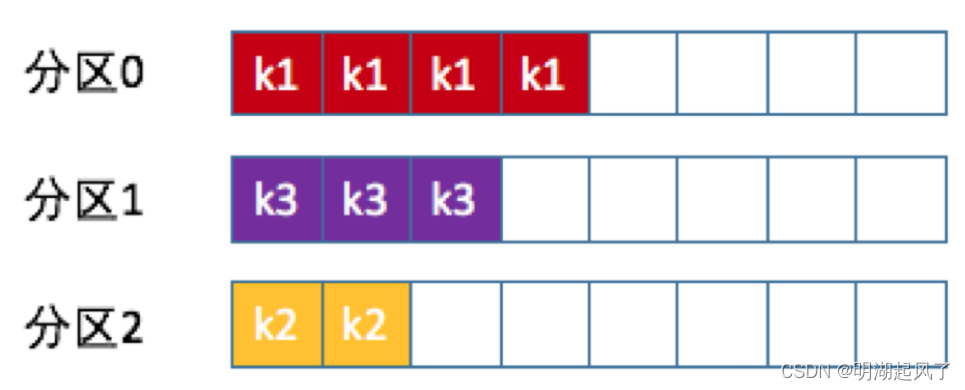
Kafka入门-分区及压缩
一、生产者消息分区 Kafka的消息组织方式实际上是三级结构:主题-分区-消息。主题下的每条消息只会保存在某一个分区中,而不会在多个分区中被保存多份。 分区的作用就是提供负载均衡的能力,或者说对数据进行分区的主要原因,就是为…...

被⽹络罪犯利⽤的5⼤ChatGPT越狱提⽰
⾃ChatGPT发布的近18个月以来,⽹络罪犯们已经能够利⽤⽣成式AI进⾏攻击。OpenAI在其内容政策中制定了限制措施,以阻⽌⽣成恶意内容。作为回应,攻击者们创建了⾃⼰的⽣成式AI平台,如 WormGPT和FraudGPT,并且他们还分享了…...
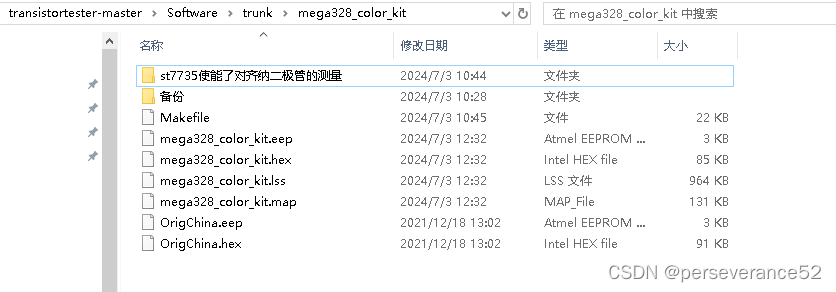
AVR晶体管测试仪开源制作与验证
AVR晶体管测试仪开源制作与验证 📍原项目地址:https://www.mikrocontroller.net/articles/AVR_Transistortester github地址:https://github.com/Mikrocontroller-net/transistortester 🎈EasyEDA项目地址:https://osh…...

头条系统-05-延迟队列精准发布文章-概述添加任务(db和redis实现延迟任务)、取消拉取任务定时刷新(redis管道、分布式锁setNx)...
文章目录 延迟任务精准发布文章 1)文章定时发布2)延迟任务概述 2.1)什么是延迟任务2.2)技术对比 2.2.1)DelayQueue2.2.2)RabbitMQ实现延迟任务2.2.3)redis实现 3)redis实现延迟任务4)延迟任务服务实现 4.1)搭建heima-leadnews-schedule模块4.2)数据库准备4.3)安装redis4.4)项目…...

不同系统间数据交换要通过 api 不能直接数据库访问
很多大数据开发提供数据给外部系统直接给表结构,这是不好的方式。在不同系统间进行数据交换时,通过API(应用程序编程接口)而非直接访问数据库是现代系统集成的一种最佳实践。 目录 为什么要通过API进行数据交换如何通过API进行数据…...
深度探索“目录名称无效“:原因、解决方案与最佳实践
目录名称无效:现象背后的秘密 在日常使用电脑或移动设备时,我们时常会遇到“目录名称无效”的错误提示,这一提示仿佛是一道无形的屏障,阻断了我们与重要数据的联系。从本质上讲,“目录名称无效”意味着系统无法识别或…...

open3d基础使用-简单易懂
Open3D是一个开源库,主要用于快速开发处理3D数据的软件。它提供了丰富的数据结构和算法,支持点云、网格和RGB-D图像等多种3D数据的处理。以下是对Open3D基础使用的详细归纳和说明: 一、安装Open3D Open3D可以通过Python的包管理器pip进行安…...

【前端】HTML+CSS复习记录【5】
文章目录 前言一、padding、margin、border(边框边距)二、样式优先级三、var(使用 CSS 变量更改多个元素样式)四、media quary(媒体查询)系列文章目录 前言 长时间未使用HTML编程,前端知识感觉…...

三分钟看懂SMD封装与COB封装的差异
全彩LED显示屏领域中,COB封装于SMD封装是比较常见的两种封装方式,SMD封装产品主要有常规小间距以及室内、户外型产品,COB封装产品主要集中在小间距以及微间距系列产品中,今天跟随COB显示屏厂家中品瑞一起快速看懂SMD封装与COB封装…...
深入理解策略梯度算法
策略梯度(Policy Gradient)算法是强化学习中的一种重要方法,通过优化策略以获得最大回报。本文将详细介绍策略梯度算法的基本原理,推导其数学公式,并提供具体的例子来指导其实现。 策略梯度算法的基本概念 在强化学习…...

Unicode 和 UTF-8 以及它们之间的关系
通俗易懂的 Unicode 和 UTF-8 解释 Unicode 是什么? 想象一下,我们有一个巨大的图书馆,这个图书馆里有各种各样的书,每本书都有一个唯一的编号。Unicode 就像是这个图书馆的目录系统,它给世界上所有的字符࿰…...

【C++】多态详解
💗个人主页💗 ⭐个人专栏——C学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 一、多态概念 二、多态的定义及实现 1. 多态的构成条件 2. 虚函数 2.1 什么是虚函数 2.2 虚函数的重写 2.3 虚函数重写的两个…...

C#异常捕获
前言 在C#中,我们无法保证我们编写的程序没有一点bug,如果我们对于这些抛出异常的bug不进行任何的处理的话,那么我们的软件在抛出这些异常的时候就会崩溃,也就是软件闪退,并且这种闪退由于我们没有进行处理࿰…...

工业一体机根据软件应用需求灵活选配
在当今工业领域,数字化、智能化的发展趋势愈发明显,工业一体机作为关键的设备,其重要性日益凸显。而能够根据软件应用需求进行灵活选配的工业一体机,更是为企业提供了高效、定制化的解决方案。 一、工业一体机的全封闭无风扇散热功…...
centos7 mqtt服务mosquitto搭建记录
1、系统centos7.6,安装默认版本 yum install mosquitto 2、启动运行 systemctl start mosquitto 3、设置自启动 systemctl enable mosquitto 4、修改配置文件 vim /etc/mosquitto/mosquitto.conf 监听端口,默认为1883,需要修改删除前面…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
