计算机图形学入门23:蒙特卡洛路径追踪
1.前言
前面几篇文章介绍了Whitted-style光线追踪,还介绍了基于物理渲染的基础知识,包括辐射度量学、BRDF以及渲染方程,但并没有给出解渲染方程的方法,或者说如何通过该渲染方程计算出屏幕上每一个坐标的像素值。
Whitted-style光线追踪是存在很多不正确的情况,但是基于渲染方程是正确的。本文就介绍通过蒙特卡洛路径追踪来解渲染方程的方法。
2.蒙特卡洛积分
蒙特卡洛积分(Monte Carlo Integration)是为了解决函数的定积分。给任意函数要算出这个函数的定积分,而定积分是一个数值。下面举个例子,如下图所示,如何去求曲线在a、b之间围成的面积。
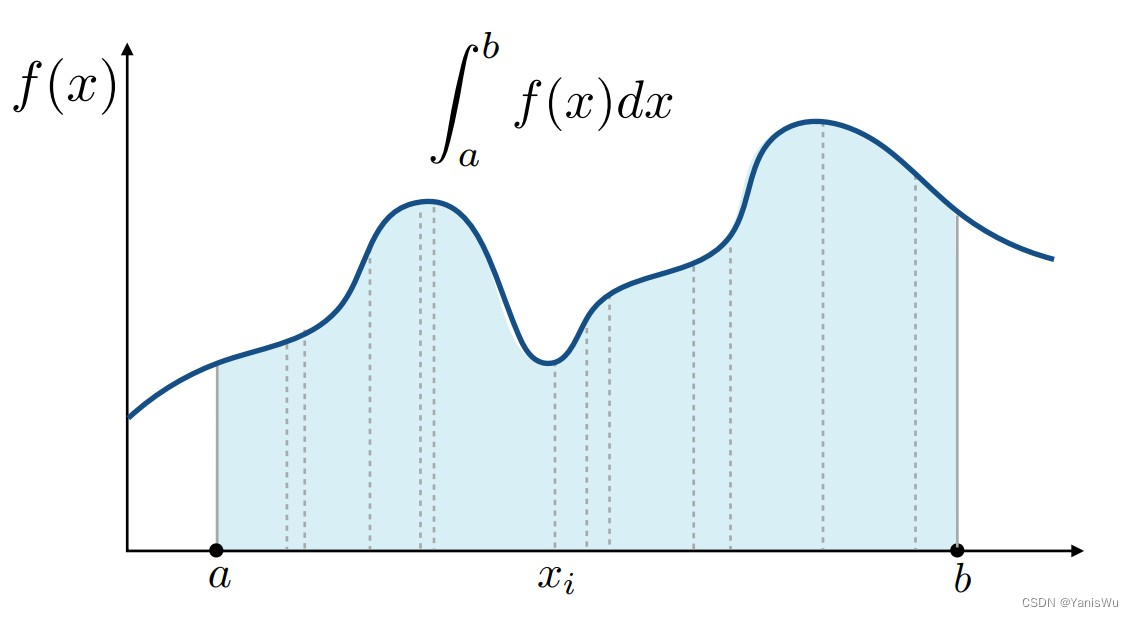
求曲线在a、b区域内面积也就是求曲线的函数在[a, b]内的定积分。但对于这样一个曲线,很难用一个数学函数去表示,因此无法用一般解析的方法直接求得积分值,可以采用黎曼积分的思路。
也就是对上图这个图形纵向均匀地切割,分成多个宽度相同的条形,那么这些条形就可以近似为长方形,取条形中线的高度作为近似长方形的高度,将这些近似小长方形的面积全部加起来就能得到整个图形近似的面积。
当切割的数量越多也就是采样越多,得到的结果越逼近真实的数值。
而相比起黎曼积分的均匀采样,蒙特卡洛积分可以指定一个随机分布来对被积分的值进行采样,因此更加通用,定义如下。
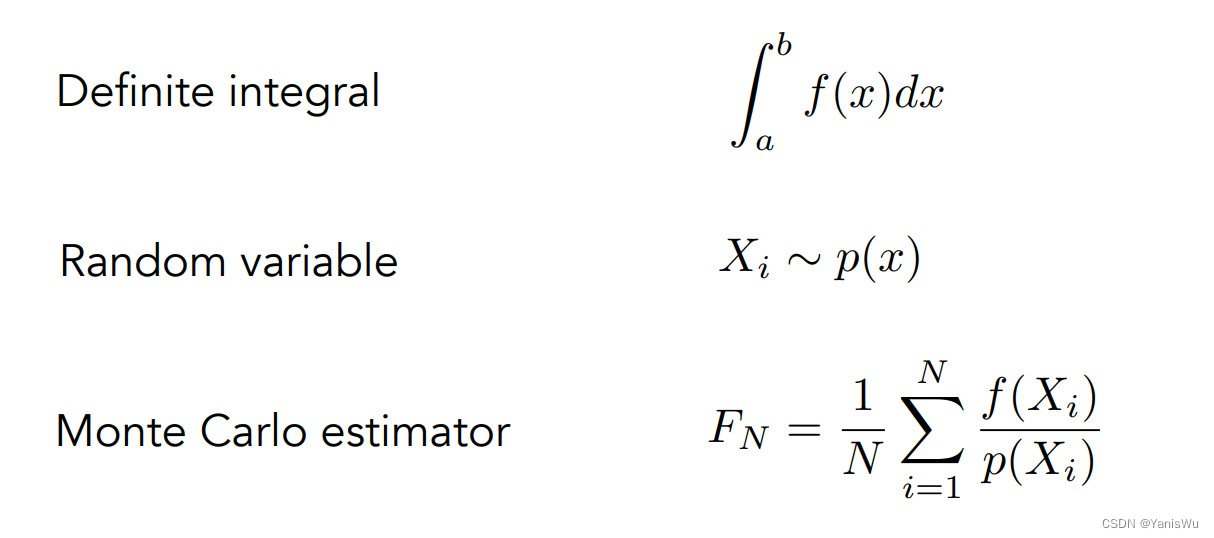
如上图所示,我们希望求出一个函数f(x)在积分域[a,b]上的积分值,选定一个采样的分布p(x),通过对该分布来进行多次的函数值采样,最后近似的积分值如图中最下方式子所示。
注意公式中的1/N可以理解为不将图形分割,而是每次采样都近似为一个采样对应的函数值的长方形,将多次采样近似的长方形面积累加求均值,如下图是采样次数为4时的。

这里对前面的公式进行一个简单的推导,从概率论的角度理解,求均值的做法其实也是对期望的逼近。

那么对于这样一个服从某一分布的期望的计算套公式直接计算得。

通过以上推导即可明白蒙特卡洛的近似正是对积分值的一个无偏估计,也就是采样次数越多,近似值与积分值越接近。简单说就是样品越多,反差越小。
为了方便,一般都使用均匀采样,因此很容易推出。

因此,蒙特卡洛就是对函数值进行多次采样求均值,从而帮助求得困难积分值的近似的方法。
3.蒙特卡洛路径追踪
3.1 Whitted-style光线追踪的问题
在前面的文章中学过Whitted-style光线追踪主要是不断在弹射光线,那么是怎么弹射光线的?
1.当光线打到表面为光滑的物体上,比如玻璃,那么光会沿着镜面方向反射或者沿着折射方向折射。
2.当光线打到漫反射物体上,光线就停了。
那么,这两个简化是对的吗?
其实,这个不一定是对的,下面举例了几个光线追踪的问题。那么,就有了路径追踪(Path Tracing)来解决很多基于非物体或者不正确的问题。
1.whited-style光线追踪对于反射表面进行镜面反射,难以模拟介于漫反射和镜面反射之间的光泽反射(Glossy Reflection)。
对于有光泽的材料,光线应该反射到哪里?如下图所示。

2.whited-style光线追踪对于漫反射表面直接进行光照计算,并没有对漫反射的光线进行追踪。
whited-style光线追踪把光线打到漫反射物体上,光线就停了,但是实际上还是有光线会反射不同方向上去。如下图所示,直接光照与全局光照的区别,全局光照图上可以看到红色和绿色墙面的颜色反射到了中间的物体表面上。

3.2 解渲染方程
3.2.1 解渲染方程的难点
上面介绍了whited-style光线追踪存在的问题,但是渲染方程是正确的,回顾渲染方程使用了各种辐射度量学、BRDF提供标准来推导出来的,方程如下。

要想解出渲染方程的解主要有两个难点:
1.半球积分的计算。考虑来至四面八方的光照,就要求整个半球(不考虑背面光)的积分。
2.递归形式。反射来的光线有可能是直接光照,也可能是其他物体反射来的间接光照。
对于第一个问题,考虑到如何用一个数值来解一个积分,就需要用到前面所学的蒙特卡洛积分了。
3.2.2 一个简单的蒙特卡洛解决方案
假设我们在以下场景中渲染一个像素(点),仅用于直接光照,场景中为面光源,如下图所示。其中ω0为眼睛的观察方向,ωi则是各个方向弹射到点 p 的光线(这里箭头方向与光线实际方向相反是因为渲染方程中所有方向都以表面向外为正方向)。

先对渲染方程稍微做一下滥用,舍弃自发光项(假设除了光源其他物体不会发光),从而方便进行计算推导如下。由于限定了直接光照,所以四面八方来的光只有光源自身发射的。其物理含义为着色点 p 到摄像机或人眼的Radiance值。
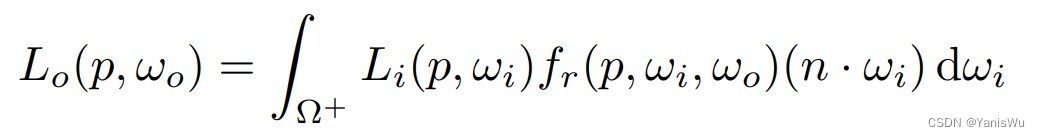
这个方程看起来很复杂,其实就是一个半球在不同方向上的积分,所以就用蒙特卡洛积分来求值。
回想前面所提到的,对于一个困难积分只要选定一个被积分变量的采样分布即可通过蒙特卡洛的方法得到积分结果的近似值。而此时的被积分值为入射光线方向ωi,选定采样分布p(ωi)为在 p 点的半球方向内对ωi进行均匀取样(只考虑从平面上方入射的光线,半球的立体角为2π,p(wi)为1/2π),不难得出积分近似结果如下:

到此时可以算出任何一个着色点出射的Radiance。对这个着色点 p 出射方向为,要计算来至四面八方光线对这个点直接光照的贡献,就可以写出一个算法,如下伪代码所示。

L_i 代表光源亮度(Radiance),f_r 代表BRDF,pdf(wi) 代表均匀采样的值。
3.2.3 全局照明
上述只考虑直接光照显然是不够的,还需要间接光照,即当采样的ωi方向碰撞到了别的物体,如下图所示。

此时采样的光线ωi碰撞到了另一个物体的Q点,如果这条光线在Q点反射后没有碰到光源,这条路径自然没有贡献;如果光线在Q点反射后碰到了光源,那么该条路径对着色点P的贡献是多少呢?
此时可以理解为ωi方向为Q点的观察方向,求Q点到ωi方向的Radiance值,也就是光源在点Q的直接光照再乘上Q点发射到ωi方向的比例。
显然这是一个类似光线追踪的递归过程,不同点是该方法通过对光线方向的采样从而找出一条条可以连接眼睛和光源的的光线路径,这也正是为什么叫路径追踪的原因,伪代码如下:

在Q点反射过来的Radiance,就相当于在Q点反射过来的直接光照,也就是在Q点从-wi方向看过去的直接光照。这里是-wi方向是因为从P点到Q点是wi方向,那么从Q点到P点自然就是-wi。
至此,我们成功通过蒙特卡洛的方式解出(近似)了渲染方程的积分值,也通过考虑直接光照与间接光照解决了递归的问题。到此,是否已经解决了?
3.2.4 路径追踪(Path Tracing)
接上述疑问,还有两个问题。
1.随着反射增加,射线爆炸。
如下图所示,我们通过每次对光线方向的采样从而解出方程,假设有一条光线打到物体上,为了计算直接光照,假如从物体上打出100条光线,那么100条都有可能打到其他物体上,在其他物体上又要算直接光照,那么每条再发射100条光线,就是10000条,依次类推,反射越多次光线数量便会指数级爆炸增长,计算量完全无法接受,那么如何才能使得光线数量不爆炸增长呢?
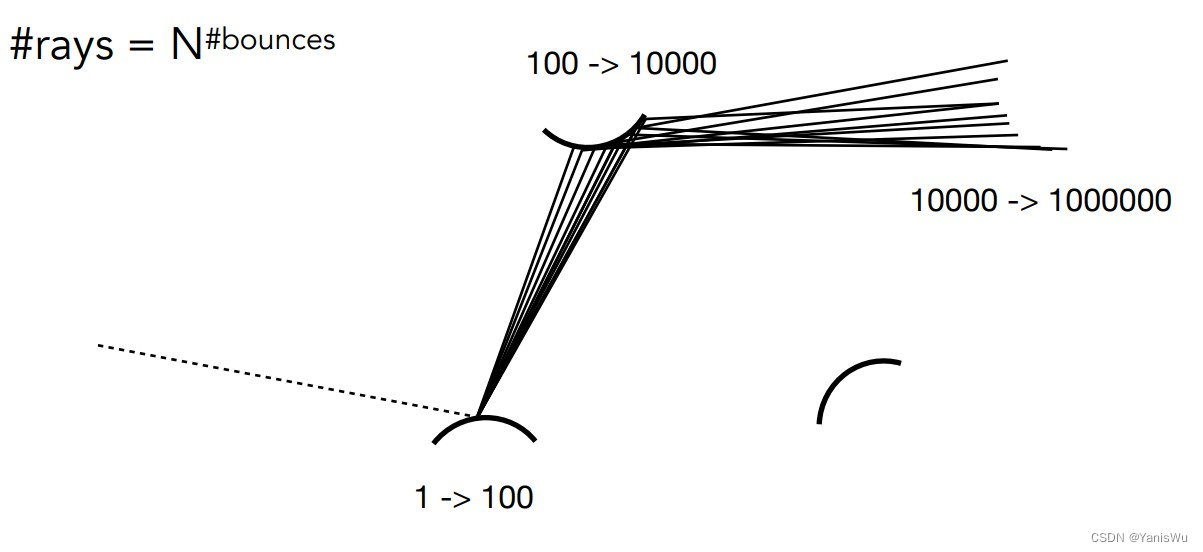
唯有每次只采样一个方向,也就是N = 1(1的多少次方都是1)。N = 1时就是通常所说的路径追踪(连接一条视点与光源的路径),作为区分N != 1时,一般称为分布式路径追踪。
从现在开始,我们总是假设每个着色点只有一条光线被追踪,伪代码如下。

如果只采样一个方向那么所带来的问题也是显而易见的,积分计算的结果会非常的随机,虽然蒙特卡洛积分是无偏估计,但样本越少显然偏差越大。
但该问题也好解决,如果每次只去寻找一条路径结果不准确,那么就去寻找多条路径。如下图所示,分别有红、蓝、黑三条路径。

从摄像机向每个像素的区域内发射多条路径,追踪每条路径的反射并计算,最后将多条路径的结果求平均即可。伪代码如下。

到此解决了射线爆炸问题,但还没有彻底解决,因为shade函数的递归没有出口,永远不会停下。
因为在现实中光线是经过无数次反射的,如果在这里给光线追踪算法中设定最大反射次数的方式,这样就会导致能量损失,所以这里非常精妙的采用了俄罗斯轮盘赌(Russian Roulette)。

一把弹仓6发的左轮手枪,随机填充两发子弹,按下扳机时,目标有4/6的概率活下来,这就是俄罗斯轮盘赌的概念。
假设一个着色点出射的结果为Lo,期望递归停止后返回的结果还是Lo。那么,首先设定一个概率P(0<P<1),每次光线反射时有P的概率光线会继续递归并设置返回值为Lo/P,有1-P的概率光线停止递归,并返回0。这样巧妙的设定之下光线一定会在某次反射之后停止递归,并且计算的结果依然是无偏的,因为从概率论的角度来看,Radiance的期望Lo不变,证明如下。
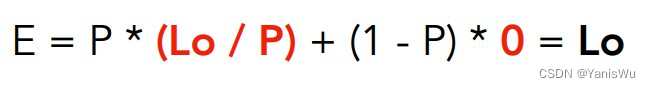
shade函数的伪代码变更如下。

至此,路径追踪算法已经完成大半,只差最后一个小问题!
2.现在的路径追踪效率非常的低下
如下图所示,图中顶部为面光源,中间为遮挡物。左图表示每个像素使用更少的采样(Low SPP),右图是每个像素使用更高的采样(High SPP)。可以发现采样点更多,效果越好,越干净(噪点少),所以效率很低,最好在Low SPP情况下也能达到很好的效果。有没有办法呢?

其实是有办法提高效率的,如下图所示就是造成低效率的原因。
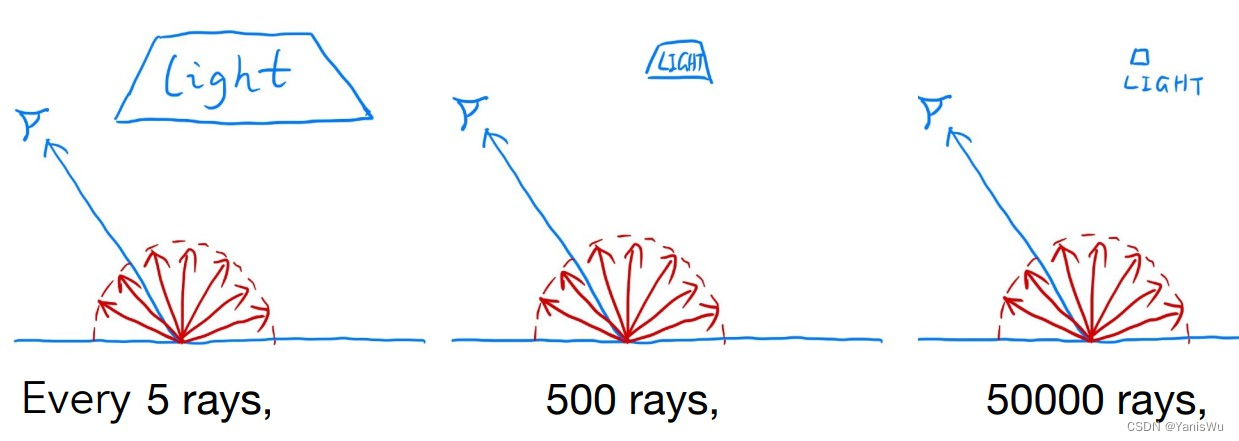
在每次计算直接光照的时候,通过均匀采样随机方向打出光线,但只有极少数的光线方向可以碰到光源,尤其当光源越小的时候,这种现象越明显,大量采样的光线都是无效浪费的。
蒙特卡洛方法允许任何采样方法,不仅限于均匀采样。因此我们可以直接对光源进行采样(如果没有别的物体遮挡,光线没有被“浪费”)。
假设光源的面积为A,那么对光源进行的采样分布p(A) = 1/A (因为光源面积p(dA)积分起来为1),但原始的渲染方程:

很明显是对光线方向ωi进行积分的,如果想要对光源进行采样并依然使用蒙特卡洛的方法,那么一定要将其修改为对光源面积 dA 的积分(改变积分域),换言之就是需要找到 dA 与 dω 的关系。如下图所示。
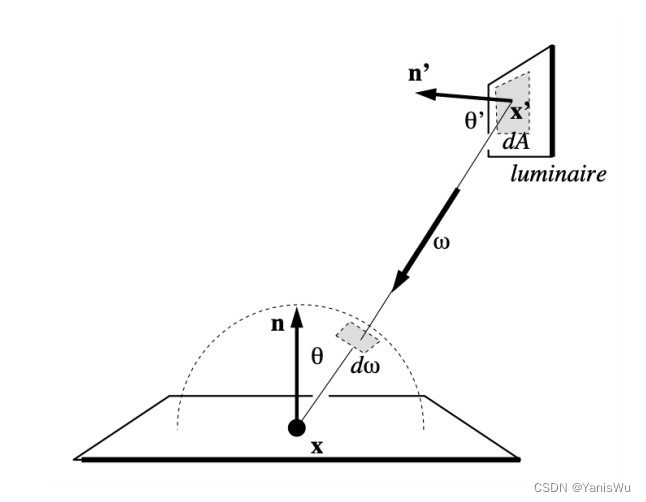
dA 与 dω 的关系如下。
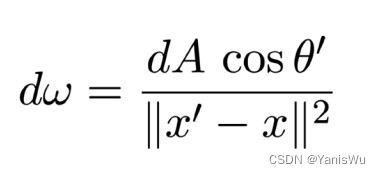
关系式中的 cosθ’ 是为了计算出光源上微分面积元正对半球的面积,之后再按照立体角的定义dω = dA / rr,即除以着色点x与光源采样点 x’ 距离的平方。
于是根据图中二者的关系可将渲染方程改写如下。
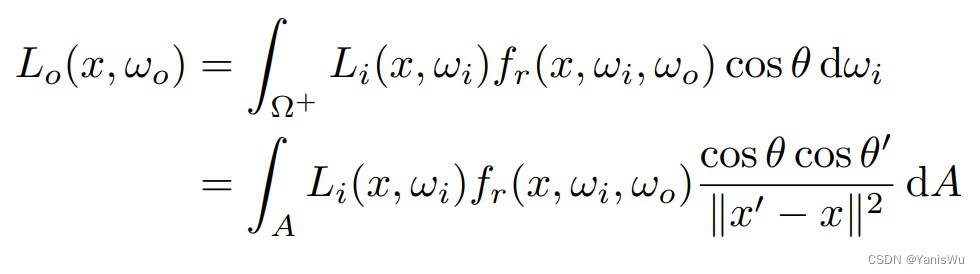
这样便成功从对 ωi 的积分转到了对光源面积 A 的积分,然后就可以利用蒙特卡洛的方法对光源进行采样从而计算直接光照的积分值,因为是对光源进行采样所以就不需要俄罗斯轮盘赌了(不涉及弹射)。对于间接光照,依然采用先前的方法进行光线方向的均匀采样。最终伪代码如下,分直接光照和间接光照两部分计算。

计算直接光照的时候还需要判断光源与着色点之间是否有物体遮挡,该做法也很简单,只需从着色点 x 向光源采样点 x’ 发出一条检测光线判断是否与光源之外的物体相交即可,如图所示。
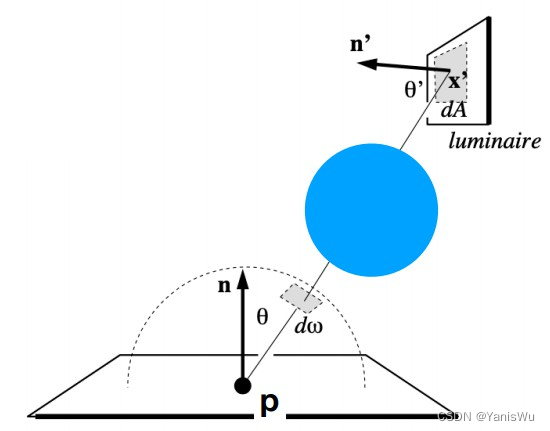
伪代码修改如下。

到这一步,路径追踪才真正完整了,路径追踪几乎可以达到100%真实感,如下图所示真实照片和路径追踪效果的对比,感受一下照片级真实(Photo-Realistic)。

3.2.5 遗留问题
1.路径追踪对点光源很难处理。只能把点光源做成面积很小的面光源。
2.路径追踪实现很困难。需要掌握的知识太多,比如物理量、微积分、概率、几何。
相关文章:

计算机图形学入门23:蒙特卡洛路径追踪
1.前言 前面几篇文章介绍了Whitted-style光线追踪,还介绍了基于物理渲染的基础知识,包括辐射度量学、BRDF以及渲染方程,但并没有给出解渲染方程的方法,或者说如何通过该渲染方程计算出屏幕上每一个坐标的像素值。 Whitted-style光…...

探索 TensorFlow 模型的秘密:TensorBoard 详解与实战
简介 TensorBoard 是 TensorFlow 提供的可视化工具,帮助开发者监控和调试机器学习模型。它提供了多种功能,包括查看损失和精度曲线、可视化计算图、检查数据分布等。下面将介绍如何使用 TensorBoard。 1. 安装 TensorBoard 如果尚未安装 TensorBoard&…...
yolov8obb角度预测原理解析
预测头 ultralytics/nn/modules/head.py class OBB(Detect):"""YOLOv8 OBB detection head for detection with rotation models."""def __init__(self, nc80, ne1, ch()):"""Initialize OBB with number of classes nc and la…...
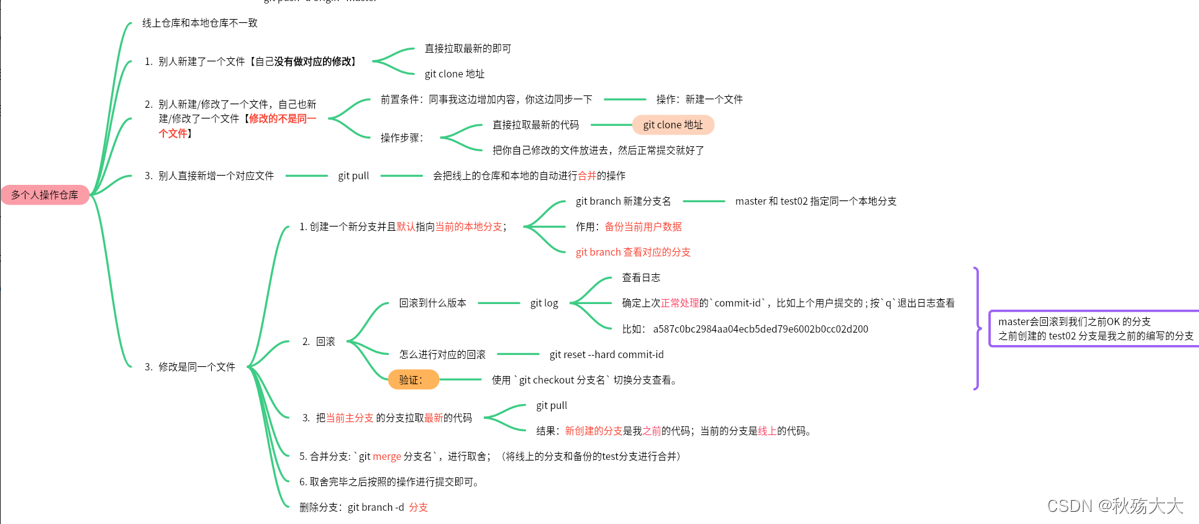
CICD之Git版本管理及基本应用
CICD:持续集成,持续交付--让对应的资料,对应的项目流程更加规范--提高效率 CICD 有很多的工具 GIT就是其中之一 1.版本控制概念与环境搭建 GIT的概念: Git是一款分布式源代码管理工具(版本控制工具) ,一个协同的工具。 Git得其数据更像是一系列微型文件系统的快照。使用Git&am…...

Python作用域及其应用
Python的作用域规则决定了变量在代码中的可见性和访问性。全局作用域中定义的变量可以在整个程序中访问,而局部作用域中定义的变量则只能在其被创建的函数或代码块中访问。 全局作用域与局部作用域 全局作用域中的变量通常在程序的顶层定义,可以被整个…...
谷歌上架,应用被Google play下架之后,活跃用户会暴跌?这是为什么?
在Google play上架应用,开发者们最不想到看到就是应用被下架了。这意味着所有的努力都将付诸东流,因为有的应用一但被下架,活跃用户也随之嗖嗖地往下掉,这事儿可真不是闹着玩的,严重影响了收益! 为什么你的…...

web安全渗透测试十大常规项(一):web渗透测试之Fastjson反序列化
渗透测试之Java反序列化 1. Fastjson反序列化1.1 FastJson反序列化链知识点1.2 FastJson反序列化链分析1.3.1 FastJson 1.2.24 利用链分析1.3.2 FastJson 1.2.25-1.2.47 CC链分析1.3.2.1、开启autoTypeSupport:1.2.25-1.2.411.3.2.2 fastjson-1.2.42 版本绕过1.3.2.3 fastjson…...

Unity 3D软件下载安装;Unity 3D游戏制作软件资源包获取!
Unity3D,它凭借强大的功能和灵活的特性,在游戏开发和互动内容创作领域发挥着举足轻重的作用。 作为一款顶尖的游戏引擎,Unity3D内置了先进的物理引擎——PhysX。这一物理引擎堪称业界翘楚,能够为开发者提供全方位、高精度的物理模…...

PyTorch之nn.Module与nn.functional用法区别
文章目录 1. nn.Module2. nn.functional2.1 基本用法2.2 常用函数 3. nn.Module 与 nn.functional3.1 主要区别3.2 具体样例:nn.ReLU() 与 F.relu() 参考资料 1. nn.Module 在PyTorch中,nn.Module 类扮演着核心角色,它是构建任何自定义神经网…...

2024.06.24 校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、校招 | 昂瑞微2025届校园招聘正式启动 校招 | 昂瑞微2025届校园招聘正式启动 2、实习 | 东风公司研发总院暑期实习生火爆招募中 实习 | 东风公司研发总院暑期实习生火爆招募中 3、实习…...

【C++】using namespace std 到底什么意思
📢博客主页:https://blog.csdn.net/2301_779549673 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正! 📢本文作为 JohnKi 的学习笔记,引用了部分大佬的案例 📢未来很长&a…...
基于ESP32 IDF的WebServer实现以及OTA固件升级实现记录(三)
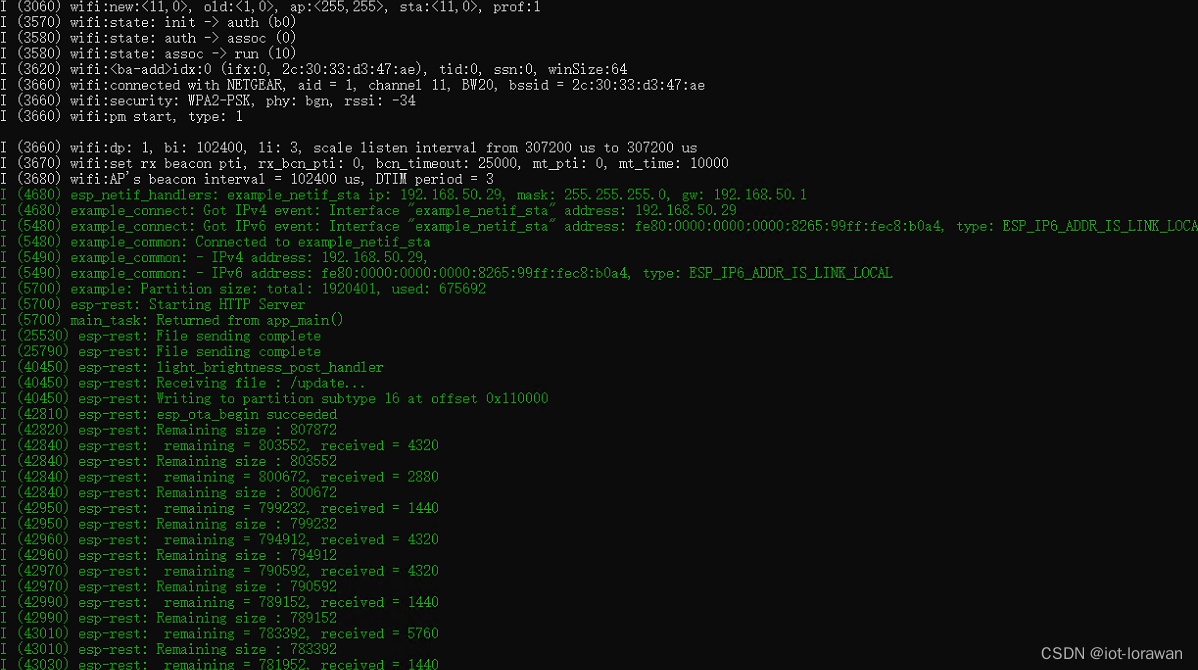
经过前面两篇的前序铺垫,对webserver以及restful api架构有了大体了解后本篇描述下最终的ota实现的代码以及调试中遇到的诡异bug。 eps32的实际ota实现过程其实esp32官方都已经基本实现好了,我们要做到无非就是把要升级的固件搬运到对应ota flash分区里面…...
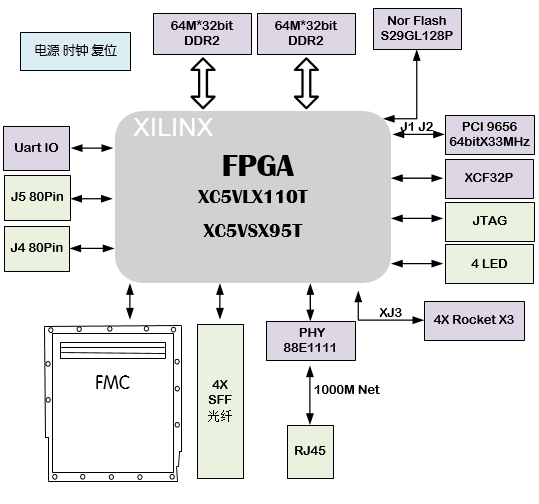
116-基于5VLX110T FPGA FMC接口功能验证6U CPCI平台
一、板卡概述 本板卡是Xilinx公司芯片V5系列芯片设计信号处理板卡。由一片Xilinx公司的XC5VLX110T-1FF1136 / XC5VSX95T-1FF1136 / XC5VFX70T-1FF1136芯片组成。FPGA接1片DDR2内存条 2GB,32MB Nor flash存储器,用于存储程序。外扩 SATA、PCI、PCI expres…...

Android - Json/Gson
Json数据解析 json对象:花括号开头和结尾,中间是键值对形式————”属性”:属性值”” json数组:中括号里放置 json 数组,里面是多个json对象或者数字等 JSONObject 利用 JSONObject 解析 1.创建 JSONObject 对象,传…...

盲信号处理的发展现状
盲源分离技术最早在上个世纪中期提出,在1991年Herault和Jutten提出基于反馈神经网络的盲源分离方法,但该方法缺乏理论基础,后来Tong和Liu分析了盲源分离问题的可辨识性和不确定性,Cardoso于1993年提出了基于高阶统计的联合对角化盲…...
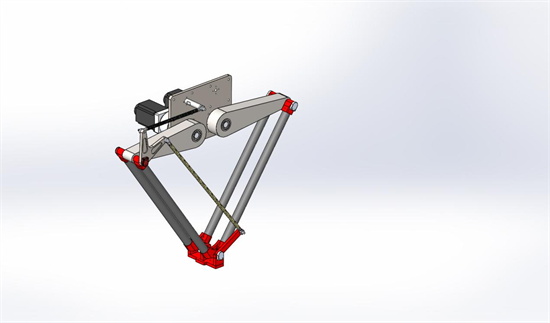
二轴机器人装箱机:重塑物流效率,精准灵活,引领未来装箱新潮流
在现代化物流领域,高效、精准与灵活性无疑是各大企业追求的核心目标。而在这个日益追求自动化的时代,二轴机器人装箱机凭借其较佳的性能和出色的表现,正逐渐成为装箱作业的得力助手,引领着未来装箱新潮流。 一、高效:重…...
使用python做飞机大战
代码地址: 点击跳转...

Python面向对象编程:派生
本套课在线学习视频(网盘地址,保存到网盘即可免费观看): https://pan.quark.cn/s/69d1cc25d4ba 面向对象编程(OOP)是一种编程范式,它通过将数据和操作数据的方法封装在一起࿰…...
华为仓颉编程语言
目录 一、引言 二、仓颉编程语言概述 三、技术特征 四、应用场景 五、社区支持 六、结论与展望 一、引言 随着信息技术的快速发展,编程语言作为软件开发的核心工具,其重要性日益凸显。近年来,华为公司投入大量研发资源,成功…...

【微信小程序开发实战项目】——如何制作一个属于自己的花店微信小程序(2)
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
