题解:CF1981C(Turtle and an Incomplete Sequence)
题解:CF1981C(Turtle and an Incomplete Sequence)
Part 1:题意理解
- 地址链接:CF、洛谷。
- 题面翻译:给定一个长度为 n n n 的序列 a a a,其中有一些元素未知,用 − 1 -1 −1 表示,现在要将数组 a a a 补充完整,即将 a a a 中所有的 − 1 -1 −1 替换成一个小于等于 1 0 9 10^9 109 的正整数,使得对于任意一个 1 ≤ i < n 1\leq i<n 1≤i<n,都有 a i = ⌊ a i + 1 2 ⌋ a_i=\left\lfloor\frac{a_{i+1}}{2}\right\rfloor ai=⌊2ai+1⌋ 或者 a i + 1 = ⌊ a i 2 ⌋ a_{i+1}=\left\lfloor\frac{a_i}{2}\right\rfloor ai+1=⌊2ai⌋。如果存在合法的方案,输出填充后的数组,否则输出 − 1 -1 −1。
- 数据范围: n ≤ 2 ⋅ 1 0 5 n\leq2\cdot10^5 n≤2⋅105,只能接受线性算法。
Part 2:算法分析
- 典型构造题。
- 首先特判,如果 a a a 中所有元素都未知,那么就 1 1 1 和 2 2 2 交替输出。
- 由于前缀和后缀的 − 1 -1 −1 都很好处理,并且对中间没有影响,先将他们特别处理。具体的,以前缀为例,假设 a 1 a_1 a1 到 a i a_i ai 均为 − 1 -1 −1,且 a i + 1 a_{i+1} ai+1 不是 − 1 -1 −1,是已知的,那么将 1 1 1 到 i i i 中所有与 i + 1 i+1 i+1 奇偶性相同的赋值为 a i + 1 a_{i+1} ai+1,其余赋值为 a i + 1 × 2 a_{i+1}\times 2 ai+1×2。
- 对于中间,每个连续的 − 1 -1 −1 组成的段是独立的,可分别处理。假设现在处理的是 a u a_u au 到 a v a_v av 这个段,我们的目标就是通过 v − u + 2 v-u+2 v−u+2 次乘 2 2 2、除以 2 2 2 的操作让 a u − 1 a_{u-1} au−1 变成 a v + 1 a_{v+1} av+1。也就是说 a u − 1 ≠ − 1 a_{u-1}\neq-1 au−1=−1, a u a_u au 到 a v a_v av 都是 − 1 -1 −1, a v + 1 ≠ − 1 a_{v+1}\neq-1 av+1=−1。根据题面分析,其实说 a i a_i ai 和 a i + 1 a_{i+1} ai+1 满足条件,实际上就是说它们在由 1 1 1 到 n n n 编号的节点组成的完全二叉树上是相邻的。因此, a u − 1 a_{u-1} au−1 通过一些操作变成 a v + 1 a_{v+1} av+1,就相当于在这棵完全二叉树上找到一个从 a u − 1 a_{u-1} au−1 走到 a v + 1 a_{v+1} av+1 的长度等于 v − u + 2 v-u+2 v−u+2 的路径。
- 如何找这条路径呢?显然,只要找出两个节点的 LCA,按照 a u − 1 a_{u-1} au−1 到 LCA 再到 a v + 1 a_{v+1} av+1 的顺序走就能得出最短的一条路径。至于怎么使它加长,就可以直接在某个点上,比如 LCA,不断地乘 2 2 2、除以 2 2 2 就可以了。当然,如果奇偶性不对,或者最短的长度也不够,自然不行。
- 但是如何实现呢?有两个指针分别指向这段未知的元素内最左侧、最右侧仍旧没有填充的位置。每一次,如果某一侧最后一个已经填充完成的数较大,就让对应侧的指针对应的元素赋值为它除以 2 2 2。如果两侧相等,就让其中一个能除以二就除以二;不能除以二,也就是说对应的已经处理完的是 1 1 1,就乘二。最后判断两个方向最后一个赋值的是否满足条件即可。
Part 3:代码实现
#include <bits/stdc++.h>
#define N 220000
using namespace std;
int t, n, a[N];
int s, lst, u, v;
bool flag;
int main() {scanf("%d", &t);while (t--) {scanf("%d", &n);s = 0;for (int i = 1; i <= n; i++) {scanf("%d", &a[i]);if (a[i] == -1) {s++;}}flag = false;for (int i = 2; i <= n; i++) {if (a[i - 1] != -1 && a[i] != -1 && a[i - 1] != a[i] / 2 && a[i] != a[i - 1] / 2) {flag = true;break;}}if (flag == true) {printf("-1\n");continue;}if (s == n) {for (int i = 1; i <= n; i++) {if (i % 2 == 0) {printf("1 ");} else {printf("2 ");}}printf("\n");} else {lst = -1;for (int i = 1; i <= n; i++) {if (a[i] != -1) {lst = i;break;}}for (int i = lst - 1; i >= 1; i--) {if (i % 2 == lst % 2) {a[i] = a[lst];} else {a[i] = a[lst] * 2;}}lst = -1;for (int i = n; i >= 1; i--) {if (a[i] != -1) {lst = i;break;}}for (int i = lst + 1; i <= n; i++) {if (i % 2 == lst % 2) {a[i] = a[lst];} else {a[i] = a[lst] * 2;}}lst = -1;flag = true;for (int i = 1; i <= n; i++) {if (a[i] == -1) {if (lst == -1) {lst = i;}if (a[i + 1] != -1) {u = lst;v = i;while (u <= v) {if (a[u - 1] > a[v + 1]) {a[u] = a[u - 1] / 2;u++;} else if (a[u - 1] < a[v + 1] ){a[v] = a[v + 1] / 2;v--;} else {if (a[u - 1] == 1) {a[u] = a[u - 1] * 2;} else {a[u] = a[u - 1] / 2;}u++;}}if (a[u] != a[v] / 2 && a[v] != a[u] / 2) {flag = false;break;}lst = -1;}}}if (flag == false) {printf("-1\n");} else {for (int i = 1; i <= n; i++) {printf("%d ", a[i]);}printf("\n");}}}return 0;
}
相关文章:
)
题解:CF1981C(Turtle and an Incomplete Sequence)
题解:CF1981C(Turtle and an Incomplete Sequence) Part 1:题意理解 地址链接:CF、洛谷。题面翻译:给定一个长度为 n n n 的序列 a a a,其中有一些元素未知,用 − 1 -1 −1 表示…...

Swift 中强大的 Key Paths(键路径)机制趣谈(上)
概览 小伙伴们可能不知道:在 Swift 语言中隐藏着大量看似“其貌不扬”实则却让秃头码农们“高世骇俗”,堪称卧虎藏龙的各种秘技。 其中,有一枚“不起眼”的小家伙称之为键路径(Key Paths)。如若将其善加利用ÿ…...

(十二)纹理和采样
纹理 在绘制三角形的过程中,将图片贴到三角形上进行显示的过程,就是纹理贴图的过程 uv坐标 如果如果图片尺寸和实际贴图尺寸不一致,就会导致像素不够用了的问题 纹理与采样 纹理对象(Texture):在GPU端,用来以一…...

QT创建地理信息shp文件编辑器shp_editor
空闲之余创建一个简单的矢量shp文件编辑器,加深对shp文件的理解。 一、启动程序 二、打开shp文件 三、显示shp文件的几何图形 四、双击右边表格中的feature,主窗体显示选中feature的各个节点。 五、鼠标在主窗体中选中feature的节点,按鼠标左…...
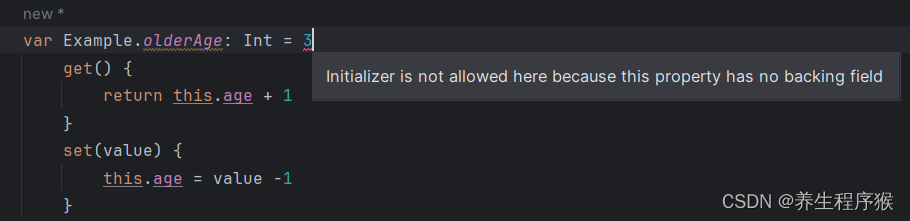
解析Kotlin中扩展函数与扩展属性【笔记摘要】
1.扩展函数 1.1 作用域:扩展函数写的位置不同,作用域就也不同 扩展函数可以写成顶层函数(Top-level Function),此时它只属于它所在的 package。这样你就能在任何类里使用它: package com.rengwuxianfun …...
【Java学习笔记】java图形界面编程
在前面的章节中,我们开发运行的应用程序都没有图形界面,但是很多应用软件,如Windows下的Office办公软件、扑克牌接龙游戏软件、企业进销存ERP系统等,都有很漂亮的图形界面。素以需要我们开发具有图形界面的软件。 Java图形界面编程…...
STM32入门笔记(03): ADC(SPL库函数版)(2)
A/D转换的常用技术有逐次逼近式、双积分式、并行式和跟踪比较式等。目前用的较多的是前3种。 A/D转换器的主要技术指标 转换时间 分辨率 例如,8位A/D转换器的数字输出量的变化范围为0~255,当输入电压的满刻度为5V时,数字量每变化…...
2024年7月2日 (周二) 叶子游戏新闻
老板键工具来唤去: 它可以为常用程序自定义快捷键,实现一键唤起、一键隐藏的 Windows 工具,并且支持窗口动态绑定快捷键(无需设置自动实现)。 卸载工具 HiBitUninstaller: Windows上的软件卸载工具 经典名作30周年新篇《恐怖惊魂夜…...

如何使用Spring Boot Profiles进行环境配置管理
如何使用Spring Boot Profiles进行环境配置管理 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨如何利用Spring Boot Profiles来管理不同环境…...
)
Java错题归纳(二)
1、若有如下接口A的定义,下列哪些类下确实现了该接口:C interface A { void method1(int i); void method2(int j); } A class B implements A{ void method1( ) { } void method2( ) { } } B class B implements A { void method1(int i ) { }…...

Grafana面试题精选和参考答案
目录 Grafana是什么以及它的主要应用场景 Grafana支持的数据源 Grafana的体系结构及主要组件 Grafana如何实现数据的可视化和监控 Grafana支持的图表类型 如何在Grafana中创建和编辑仪表盘 Grafana的查询编辑器功能 Grafana支持的认证方式 Grafana的性能调优建议 Gra…...
Node版本管理工具 fnm 安装使用
fnm 是一个基于 Rust 开发的 Node 版本管理工具,它的目标是提供一个快速、简单且可靠的方式来管理 Node.js 的不同版本。同时,它是跨平台的,支持 macOS、Linux、Windows。🚀 Fast and simple Node.js version manager, built in R…...

vector模拟实现【C++】
文章目录 全部的实现代码放在了文章末尾准备工作包含头文件定义命名空间和类类的成员变量 迭代器迭代器获取函数 构造函数默认构造使用n个值构造迭代器区间构造解决迭代器区间构造和用n个值构造的冲突拷贝构造 析构函数swap【交换函数】赋值运算符重载emptysize和capacityopera…...

《每天5分钟用Flask搭建一个管理系统》第11章:测试与部署
第11章:测试与部署 11.1 测试的重要性 测试是确保应用质量和可靠性的关键步骤。它帮助开发者发现和修复错误,验证功能按预期工作。 11.2 Flask测试客户端的使用 Flask提供了一个测试客户端,可以在开发过程中模拟请求并测试应用的响应。 …...

Landsat数据从Collection1更改为Collection2
目录 问题解决 问题 需要注意!您使用的是废弃的陆地卫星数据集。为确保功能持续,请在2024年7月1日前更新。 在使用一些以前的代码时会遇到报错,因为代码里面用的是老的数据集 解决 对于地表反射率SR,需要在name中,将C01换为C02&…...

《每天5分钟用Flask搭建一个管理系统》第12章:安全性
第12章:安全性 12.1 Web应用的安全威胁 Web应用面临的安全威胁包括但不限于跨站脚本攻击(XSS)、SQL注入、跨站请求伪造(CSRF)、不安全的直接对象引用(IDOR)等。 12.2 Flask-Talisman扩展的使…...
Unity之创建与导出PDF
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity之创建与导出PDF TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进取! 助力快速…...

【Android面试八股文】优化View层次过深问题,选择哪个布局比较好?
优化深层次View层次结构的问题,选择合适的布局方式是至关重要的。以下是几点建议: 使用ConstraintLayout:ConstraintLayout是Android开发中推荐的布局,能够有效减少嵌套,提高布局性能。相比RelativeLayout,…...

什么是带有 API 网关的代理?
带有 API 网关的代理服务显著提升了用户体验和性能。特别是对于那些使用需要频繁创建和轮换代理的工具的用户来说,使用 API 可以节省大量时间并提高效率。 了解 API API,即应用程序编程接口,是服务提供商和用户之间的连接网关。通过 API 连接…...

sql拉链表
1、定义:维护历史状态以及最新数据的一种表 2、使用场景 1、有一些表的数据量很大,比如一张用户表,大约1亿条记录,50个字段,这种表 2.表中的部分字段会被update更新操作,如用户联系方式,产品的…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...

codeforces C. Cool Partition
目录 题目简述: 思路: 总代码: https://codeforces.com/contest/2117/problem/C 题目简述: 给定一个整数数组,现要求你对数组进行分割,但需满足条件:前一个子数组中的值必须在后一个子数组中…...
