拓扑学习系列(8)黎曼度量曲面与高斯曲率
- 黎曼度量
黎曼度量是黎曼几何中的一个重要概念,它用来描述流形上的切向量之间的长度和角度。黎曼度量赋予了流形一个内积结构,使得我们可以定义切向量的长度、夹角和内积,从而引入了度量空间的概念。让我更详细地解释一下黎曼度量:
定义:
在一个光滑流形上,黎曼度量是一个定义在切空间上的双线性对称正定张量场。它可以用来度量切向量之间的长度和夹角,同时也定义了切向量的内积。
性质:
-
正定性:黎曼度量是正定的,即对于任意非零切向量,其长度的平方大于等于零,并且只有当向量为零向量时长度的平方为零。
-
对称性:黎曼度量是对称的,即对于任意两个切向量,其内积与交换向量的位置无关。
-
双线性性:黎曼度量是双线性的,即它对于两个向量是线性的,对于一个向量是另一个向量的线性。
应用:
-
测地线:黎曼度量在描述测地线(空间中最短路径)时起着关键作用,它定义了测地线的长度和弯曲性质。
-
曲率:黎曼度量也用于计算流形上的曲率,包括黎曼曲率张量和高斯曲率等,用来描述空间的弯曲程度。
-
广义相对论:在爱因斯坦的广义相对论中,引力场的描述依赖于黎曼度量,它描述了引力场对时空的弯曲。
黎曼度量是黎曼几何中的核心概念,它赋予了流形一个度量结构,使得我们可以在流形上定义长度、角度和内积,进而研究空间的几何性质和曲率。黎曼度量在数学、物理学和工程领域具有广泛的应用和重要性。
在数学中,黎曼度量是定义在流形上的一个概念,它赋予了流形一个内积结构,用来度量切向量之间的长度和夹角。下面是对黎曼度量的严格定义:
设 MM 是一个 nn 维光滑流形,T_pMTpM 表示在点 p \in Mp∈M 处的切空间,g_pgp 是定义在 T_pMTpM 上的一个对称双线性形式。如果对于任意 p \in Mp∈M,g_pgp 是正定的,即对任意非零切向量 v \in T_pMv∈TpM,有 g_p(v, v) > 0gp(v,v)>0,且只有当 v = 0v=0 时等号成立,那么称 gg 是 MM 上的一个黎曼度量。
换句话说,黎曼度量 gg 是一个定义在流形 MM 上的切空间 T_pMTpM 上的一个对称双线性形式,满足正定性和对称性。正定性保证了长度的非负性和零长度只有在零向量上达到,对称性保证了内积的对称性。
黎曼度量在流形上赋予了一种度量结构,使得我们可以定义长度、角度和内积,从而可以研究流形的几何性质、曲率和测地线等概念。在黎曼几何中,黎曼度量是一个非常重要的概念,它为研究流形的几何性质提供了基础。
- 黎曼度量曲面
在数学中,黎曼度量曲面指的是一个二维曲面,其上定义了一个黎曼度量。黎曼度量曲面在几何学和微分几何中具有重要的应用,它可以用来描述曲面上的长度、角度和内积,从而研究曲面的几何性质和曲率。让我详细解释一下黎曼度量曲面的概念:
定义:
设 SS 是一个二维光滑曲面,gg 是定义在 SS 上的一个黎曼度量。黎曼度量 gg 赋予了曲面 SS 的切空间一个内积结构,使得我们可以度量切向量之间的长度和夹角。
性质:
-
正定性:黎曼度量曲面上的度量是正定的,即对于任意非零切向量,其长度的平方大于零,并且只有当向量为零向量时长度的平方为零。
-
对称性:黎曼度量是对称的,即内积与交换向量的位置无关。
-
双线性性:黎曼度量是双线性的,对于两个向量是线性的,对于一个向量是另一个向量的线性。
应用:
-
测地线:黎曼度量曲面上的测地线是曲面上的最短曲线,类似于直线在欧几里得空间中的性质,它描述了曲面上的最短路径。
-
曲率:黎曼度量曲面上的曲率描述了曲面的弯曲性质,包括高斯曲率、平均曲率等概念,用来研究曲面的几何性质和曲率变化。
-
微分几何:黎曼度量曲面是微分几何中的重要对象,它为研究曲面的几何性质、流形的曲率和拓扑提供了重要的工具和理论基础。
黎曼度量曲面是黎曼几何中的一个重要研究对象,它在数学、物理学和工程领域具有广泛的应用和重要性,为研究曲面的几何性质和曲率提供了有力的工具和理论基础。
- 高斯曲率
高斯曲率是描述曲面局部几何性质的一个重要概念,它衡量了曲面在某一点处的曲率情况。高斯曲率通常用 KK 表示,是一个标量,可以帮助我们理解曲面的弯曲程度和拓扑特征。下面是对高斯曲率的解释:
定义:
给定一个光滑曲面,以及曲面上的一个点 pp,高斯曲率 KK 可以通过该点处的曲率信息计算得出。在欧几里得空间中,高斯曲率可以通过曲面在该点处的法向曲率的乘积来表示。
物理意义:
-
凹凸性:高斯曲率可以帮助我们判断曲面在某一点处是凹的还是凸的。当高斯曲率为正时,曲面是凸的;当高斯曲率为负时,曲面是凹的。
-
弯曲程度:高斯曲率的绝对值越大,曲面在该点处的弯曲程度越大。高斯曲率为零的点被称为拐点,表示曲面在该点处是平坦的。
应用领域:
-
微分几何:高斯曲率是微分几何中的一个重要概念,它与曲面的几何性质密切相关,用来研究曲面的曲率和拓扑特征。
-
计算机图形学:高斯曲率在计算机图形学中被广泛应用,用来描述曲面的形状和弯曲特征,帮助实现真实感的渲染效果。
-
物理学:在物理学领域,高斯曲率在描述引力场、黑洞和宇宙拓扑等方面起着重要作用,与时空的几何结构密切相关。
高斯曲率是描述曲面局部几何性质的一个重要量,它提供了关于曲面弯曲程度和拓扑结构的重要信息。通过研究高斯曲率,我们可以更深入地理解曲面的形状特征和几何性质。
在数学中,高斯曲率是描述曲面曲率性质的一个重要概念,它可以通过曲面上的度量张量来定义。让我为您严格定义高斯曲率:
设 SS 是一个光滑曲面,gg 是定义在 SS 上的黎曼度量,KK 是高斯曲率。在曲面上选取一个局部坐标系,对于任意两个切向量 v, wv,w,它们在该坐标系下的内积为 g(v, w)g(v,w)。高斯曲率 KK 可以通过该局部坐标系下的曲率张量 RR 计算得出:
K = \frac{R_{1212}}{g_{11}g_{22} - g_{12}^2}K=g11g22−g122R1212
其中,R_{1212}R1212 是曲率张量的 (1,2,1,2)(1,2,1,2) 分量,g_{ij}gij 是度量张量的分量。
性质:
-
拐点:高斯曲率为零的点被称为拐点,表示曲面在该点处是平坦的。
-
凹凸性:当高斯曲率为正时,曲面是凸的;当高斯曲率为负时,曲面是凹的。
-
弯曲程度:高斯曲率的绝对值越大,曲面在该点处的弯曲程度越大。
应用:
-
微分几何:高斯曲率是微分几何中的一个重要概念,用来描述曲面的曲率性质和拓扑特征。
-
计算机图形学:高斯曲率在计算机图形学中被广泛应用,用来描述曲面的形状和弯曲特征,帮助实现真实感的渲染效果。
-
物理学:高斯曲率在描述引力场、黑洞和宇宙拓扑等方面起着重要作用,与时空的几何结构密切相关。
高斯曲率是一个重要的几何量,它提供了关于曲面曲率和弯曲性质的重要信息。通过研究高斯曲率,我们可以深入理解曲面的几何特征和形状性质。
- 曲面Ricci流
曲面上的Ricci流是一个重要的几何流,描述了曲面上度量的演化过程。Ricci流是指曲面上的度量按照Ricci曲率的梯度方向进行演化的过程。让我为您解释一下曲面Ricci流的概念:
定义:
考虑一个二维曲面 MM 上的一个初始黎曼度量 g_0g0,Ricci流是指通过下面的偏微分方程来演化度量 g_tgt 的过程:
\frac{\partial g_t}{\partial t} = -2 \text{Ric}(g_t)∂t∂gt=−2Ric(gt)
其中,\text{Ric}(g_t)Ric(gt) 是度量 g_tgt 的Ricci曲率张量,表示了在该度量下切向量的收缩情况。
物理意义:
Ricci流描述了曲面上度量的变化规律,通过度量矩阵中的Ricci曲率来指导度量的演化方向。Ricci流可以帮助我们理解曲面的几何形变和拓扑变化。
应用:
-
流形演化:Ricci流在流形演化和几何分析中具有重要作用,可以帮助研究流形的几何性质和形变过程。
-
拓扑优化:Ricci流也在拓扑优化和表面重建中被广泛应用,可以优化曲面的拓扑结构和几何形状。
-
几何流:Ricci流是几何流理论中的一个重要分支,与流形上的度量和曲率密切相关,为几何分析和流形学习提供了重要工具。
曲面Ricci流是一个重要的几何流,描述了度量在曲面上的演化过程,通过Ricci曲率来指导度量的变化方向。通过研究Ricci流,我们可以深入理解曲面的几何性质和演化规律。
- 曲面微分几何
曲面微分几何是研究曲面及其上的几何结构和性质的数学分支。它主要关注曲面上的切空间、切向量、曲率、测地线等几何概念,并通过微分几何的方法来研究曲面的性质。让我为您详细解释一下曲面微分几何的概念:
主要内容:
-
切空间和切向量:在曲面微分几何中,切空间是曲面上每一点的切向量构成的空间,切向量是表示曲面上切线方向的概念,它们在曲面上的运算和性质是曲面微分几何的基础。
-
第一基本形式:第一基本形式是描述曲面上的度量结构的工具,它可以用来计算曲面上的长度、夹角和曲率等几何量。
-
曲率:曲率是曲面微分几何中一个重要的概念,包括高斯曲率、平均曲率、曲率张量等,用来描述曲面的弯曲性质和几何变化。
-
测地线:测地线是曲面上的最短曲线,类似于直线在欧几里得空间中的性质,它是曲面微分几何中的重要研究对象。
-
黎曼度量:黎曼度量是定义在曲面上的一个内积结构,用来度量切向量间的长度和夹角,是曲面微分几何中的核心概念之一。
应用领域:
-
地质学:曲面微分几何在地质学中被用来分析地形地貌的特征和变化规律。
-
计算机图形学:曲面微分几何在计算机图形学中被广泛应用,用来建模和渲染曲面形状。
-
物理学:在物理学领域,曲面微分几何被用来描述时空的几何结构和引力场。
曲面微分几何是一个重要的数学分支,它为研究曲面的几何性质和曲率提供了重要的工具和理论基础。通过曲面微分几何的研究,我们可以深入理解曲面的几何特征和形状性质。
相关文章:
黎曼度量曲面与高斯曲率)
拓扑学习系列(8)黎曼度量曲面与高斯曲率
黎曼度量 黎曼度量是黎曼几何中的一个重要概念,它用来描述流形上的切向量之间的长度和角度。黎曼度量赋予了流形一个内积结构,使得我们可以定义切向量的长度、夹角和内积,从而引入了度量空间的概念。让我更详细地解释一下黎曼度量࿱…...
:i.MX linux BSP)
汽车IVI中控开发入门及进阶(三十四):i.MX linux BSP
开发板: 汽车IVI中控开发入门及进阶(三十三):i.MX linux开发之开发板-CSDN博客 linux 开发项目: 汽车IVI中控开发入门及进阶(三十二):i.MX linux开发之Yocto-CSDN博客 前言: 有了开发板,linux BSP编译项目yocto,接下来就可以在i.MX平台上构建和安装i.MX Linux …...

【Python机器学习】算法链与管道——构建管道
目录 1、首先,我们构建一个由步骤列表组成的管道对象。 2、向任何其他scikit-learn估计器一样来拟合这个管道 3、调用pipe.score 我们来看下如何使用Pipeline类来表示在使用MinMaxScaler缩放数据后,再训练一个SVM的工作流程(暂时不用网格搜…...

Postman 高级用法学习
Postman 高级用法 Postman 是一款强大的 API 调试和开发工具,广泛应用于 API 开发、测试、调试和自动化流程中。除了基本的 API 请求发送和响应查看功能,Postman 还提供了许多高级功能。以下是详细的讲解,包括具体示例和操作步骤。 一、环境…...
)
从新手到高手:Scala函数式编程完全指南,Scala 访问修饰符(6)
1、Scala 访问修饰符 Scala 访问修饰符基本和Java的一样,分别有:private,protected,public。 如果没有指定访问修饰符,默认情况下,Scala 对象的访问级别都是 public。 Scala 中的 private 限定符ÿ…...
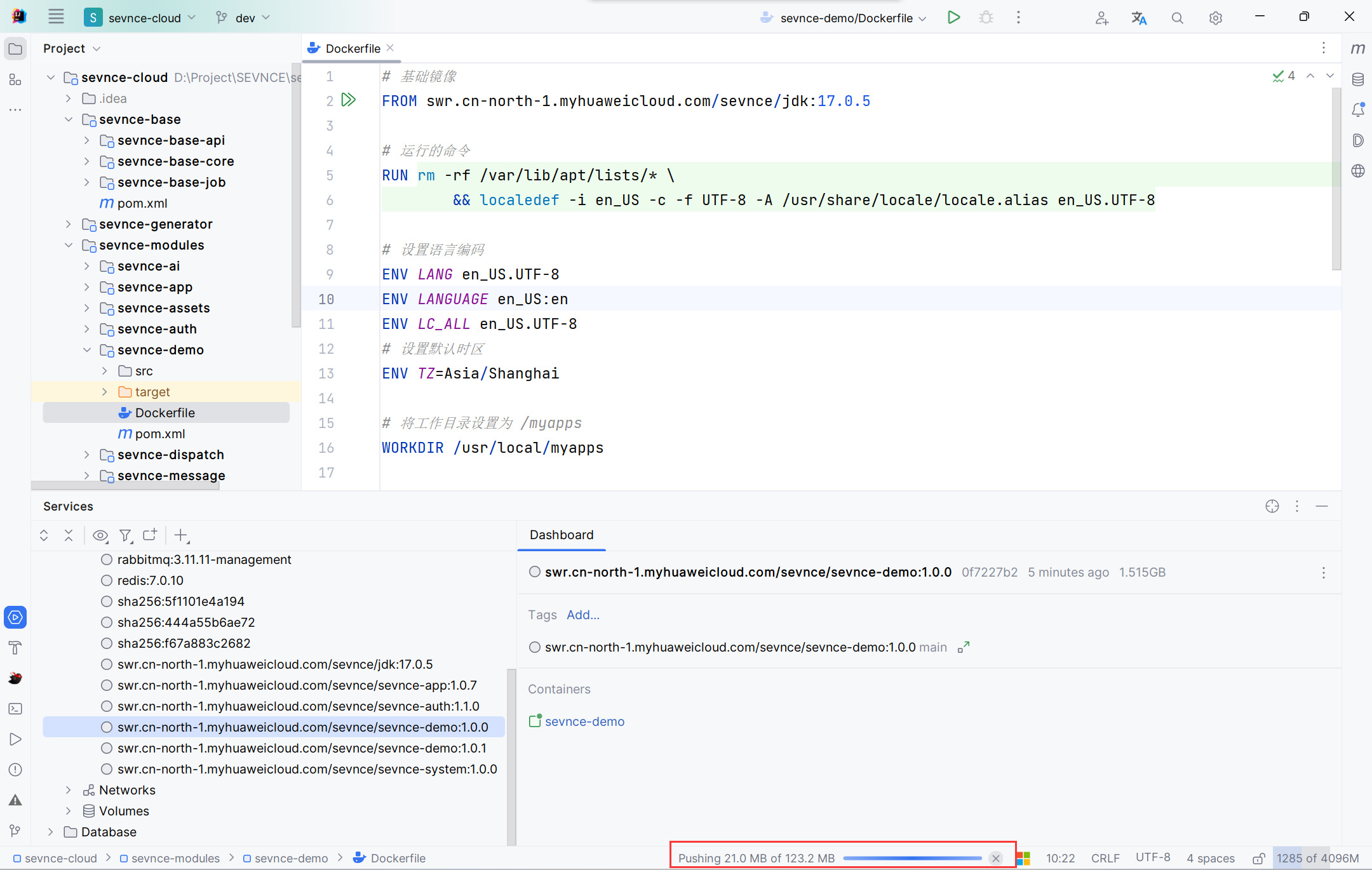
IDEA 一键部署Docker
以部署示例服务(sevnce-demo)为例。 配置服务器 地址、账号、密码根据实际情况填写 配置镜像仓库 地址、账号、密码根据实际情况填写 编写Dockerfile 在sevnce-demo根目录下右键,选择创建Dockerfile。 # 基础镜像 FROM sevnce-registry.c…...

linux centos tomcat 不安全的HTTP请求方法
1、页面查看 2、在linux主机可使用此命令查看 curl -v -X OPTIONS http://实际地址 3、进入tomcat conf目录vim web.xml,增加以下内容 <!-- close insecure http methods --> <security-constraint><web-resource-collection><web-resource…...
)
深入Django(六)
Django的表单系统 引言 在前五天的教程中,我们介绍了Django的基本概念、模型、视图、模板和URL路由。今天,我们将讨论Django的表单系统,它是处理用户输入、验证数据和与模型交互的重要组件。 Django表单系统概述 Django的表单系统提供了一…...
PHP房产小程序微信小程序系统源码
🏠—— 购房租房,一“指”搞定🏡 🔍【开篇:房产新视界,尽在掌握】 在这个信息爆炸的时代,找房子不再是一场漫长的奔波。有了“房产微信小程序”,无论是购房还是租房,都…...

vscode 历史便携版下载方法
vscode 历史版本地址 https://code.visualstudio.com/updates/v1_75#_remote-developmentexe 信息 下载链接 https://vscode.download.prss.microsoft.com/dbazure/download/stable/5437499feb04f7a586f677b155b039bc2b3669eb/VSCodeUserSetup-x64-1.90.2.exe需要使用的 com…...

深入理解计算机系统 CSAPP 家庭作业8.19
假设n1 会打印 2行 hello 假设n2 会打印 4行 hello 假设n3 会打印 8行 hello 答案 2的n次方...

JDBC学习(Java DataBase Connectivity)
JDBC简介 JDBC入门 驱动jar包:C:\Users\49960\Desktop\mysql-connector-j-9.0.0 需要配置add library!!! import java.sql.Connection; import java.sql.DriverManager; import java.sql.Statement; import java.util.Stack;pub…...

2024源代码加密软件评测丨保护企业源代码防泄密
为什么需要对源代码进行加密?因为源代码泄密可能会带来一系列严重的后果: 源代码泄密会导致企业的知识产权被盗窃,竞争对手可能会利用这些代码开发类似的产品,从而削弱公司的市场竞争力。 由于知识产权被盗,公司可能会…...

测试图片上传功能,使用postman提供的url
是不是有时候想要测试图片上传功能,但是没有后台url进行测试,这时候就可以使用postman提供的url: https://postman-echo.com/post接下来,我将教你在postman中,用该url测试图片上传功能。 1.发送图片上传请求 第一步…...

使用dot来画流程图
Dot是一种图形描述语言,属于Graphviz软件的一部分。Graphviz是一个用于可视化图形(图表、网络图等)的开源工具集。使用Dot语言,你可以创建并描述节点和边,从而生成图形。以下是如何使用Dot语言画图的基本步骤ÿ…...

基于Java的微信记账小程序【附源码】
摘 要 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,记账微信小程序被用户普遍使用,为方便用户能够…...

uniapp中 uni.previewImage用法
查看多张照片,图片地址用逗号分隔 showimig(item) {if (item.trainingRoom) {const urls item.trainingRoom.split(,);uni.previewImage({urls: urls,current: ,success: function(res) {// 成功的回调},fail: function(res) {// 失败的回调},complete: function(…...

第十三章 StringTable
String 的基本特性 String:字符串,使用一对 “” 引起来表示 // 两种定义方式 String s1 "atguigu"; // 字面量的定义方式 String s2 new String("hello");String 声明为 final 的,不可被继承String 实现了 Serializ…...
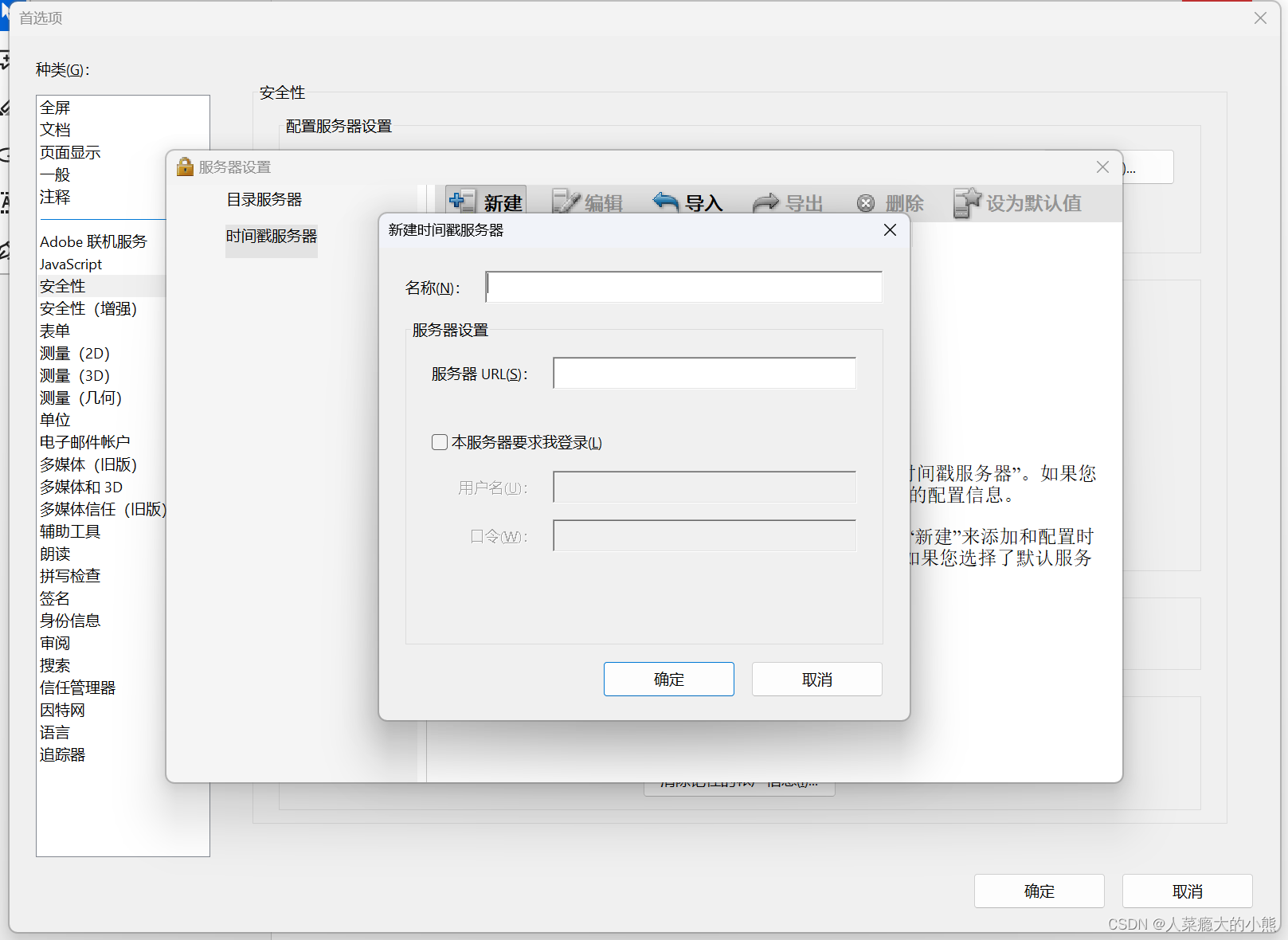
Adobe Acrobat添加时间戳服务器
文章目录 前言一、Adobe Acrobat添加时间戳服务器1.打开Adobe Acrobat软件2.点击【菜单】→ 【首选项】3.点击【安全性】→【更多】4.点击【新建】5.输入【名称】→【服务器URL】 前言 一、Adobe Acrobat添加时间戳服务器 1.打开Adobe Acrobat软件 2.点击【菜单】→ 【首选项…...
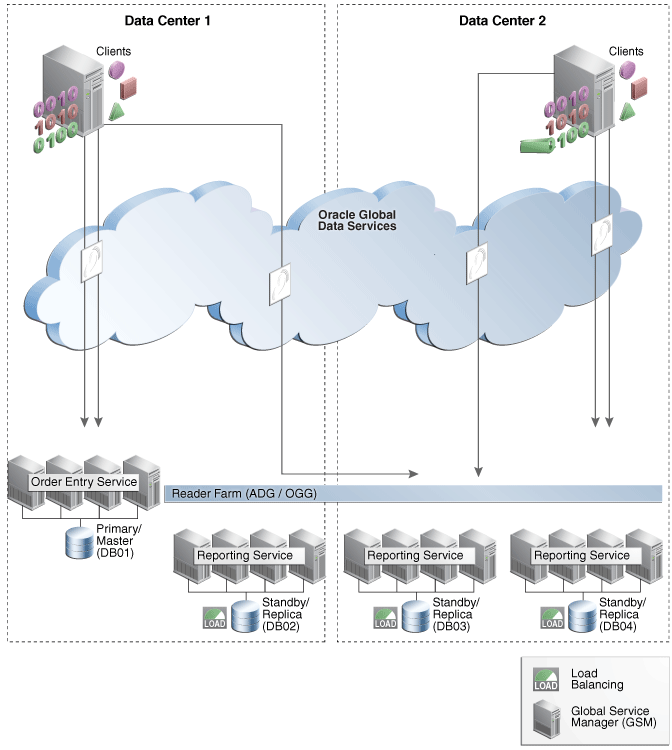
数据库管理-第217期 Oracle的高可用-02(20240704)
数据库管理217期 2024-07-04 数据库管理-第217期 Oracle的高可用-02(20240704)1 GDS简介2 GDS架构2.1 全局数据服务池2.2 全局数据服务域2.3 全局服务管理2.4 全局数据服务目录2.5 Oracle通知服务 3 GDS简图3.1 负载均衡3.2 只读服务失败转移3.3 多主复制…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...
