中位数贪心,3086. 拾起 K 个 1 需要的最少行动次数
一、题目
1、题目描述
给你一个下标从 0 开始的二进制数组
nums,其长度为n;另给你一个 正整数k以及一个 非负整数maxChanges。Alice 在玩一个游戏,游戏的目标是让 Alice 使用 最少 数量的 行动 次数从
nums中拾起k个 1 。游戏开始时,Alice 可以选择数组[0, n - 1]范围内的任何索引aliceIndex站立。如果nums[aliceIndex] == 1,Alice 会拾起一个 1 ,并且nums[aliceIndex]变成0(这 不算 作一次行动)。之后,Alice 可以执行 任意数量 的 行动(包括零次),在每次行动中 Alice 必须 恰好 执行以下动作之一:
- 选择任意一个下标
j != aliceIndex且满足nums[j] == 0,然后将nums[j]设置为1。这个动作最多可以执行maxChanges次。- 选择任意两个相邻的下标
x和y(|x - y| == 1)且满足nums[x] == 1,nums[y] == 0,然后交换它们的值(将nums[y] = 1和nums[x] = 0)。如果y == aliceIndex,在这次行动后 Alice 拾起一个 1 ,并且nums[y]变成0。返回 Alice 拾起 恰好
k个 1 所需的 最少 行动次数。
2、接口描述
python3
class Solution:def minimumMoves(self, nums: List[int], k: int, maxChanges: int) -> int:cpp
class Solution {
public:long long minimumMoves(vector<int>& nums, int k, int maxChanges) {}
};js
/*** @param {number[]} nums* @param {number} k* @param {number} maxChanges* @return {number}*/
var minimumMoves = function(nums, k, maxChanges) {};
3、原题链接
3086. 拾起 K 个 1 需要的最少行动次数
二、解题报告
1、思路分析
操作1其实就是提供了一种两步得到1的方案
我们考虑两步一个1一定是最优的吗?
如果1、2、3个连续个1,我们发现此时分别需要0、1、2步
所以这道题是有corner case的
我们这样考虑
3个以内的连续1的最大连续长度记为c,如果拿掉c个剩下的1可以都通过2步得到
我们的答案就是c - 1 + (k - c) * 2
否则,问题就变成了一个很简单的中位数贪心问题
扫描一遍k - maxChanges的窗口,O(1)计算其中位数贪心下的解维护最优解即可
2、复杂度
时间复杂度: O(N)空间复杂度:O(N)
3、代码详解
python3
fmax = lambda x, y: x if x > y else y
fmin = lambda x, y: x if x < y else y
class Solution:def minimumMoves(self, nums: List[int], k: int, maxChanges: int) -> int:pos = []c = 0for i, x in enumerate(nums):if x == 0:continuepos.append(i)c = fmax(c, 1)if i > 0 and nums[i - 1]:if i > 1 and nums[i - 2]:c = 3c = fmax(c, 2)c = fmin(c, k)if maxChanges >= k - c:return fmax(c - 1, 0) + (k - c) * 2n = len(pos)acc = list(accumulate(pos, initial=0))res = infsz = k - maxChangesfor r in range(sz, n + 1):l = r - szmid = l + sz // 2s1 = pos[mid] * (mid - l) - (acc[mid] - acc[l])s2 = acc[r] - acc[mid] - pos[mid] * (r - mid)res = fmin(res, s1 + s2)return res + maxChanges * 2
cpp
class Solution {
public:long long minimumMoves(vector<int>& nums, int k, int maxChanges) {int c = 0;std::vector<int> pos;for (int i = 0, n = nums.size(); i < n; i ++ ) {if (!nums[i]) continue;pos.push_back(i);c = max(c, 1);if (i && nums[i - 1]) {if (i > 1 && nums[i - 2])c = 3;c = max(c, 2);}}c = min(c, k);if (maxChanges >= k - c)return max(c - 1, 0) + (k - c) * 2;int n = pos.size(), sz = k - maxChanges;std::vector<long long> acc(n + 1);for (int i = 0; i < n; i ++ ) acc[i + 1] = acc[i] + pos[i];long long res = 1e10;for (int r = sz; r <= n; r ++ ) {int l = r - sz, mid = l + sz / 2;long long s1 = 1LL * pos[mid] * (mid - l) - (acc[mid] - acc[l]);long long s2 = acc[r] - acc[mid] - 1LL * pos[mid] * (r - mid);res = min(res, s1 + s2);\}return res + maxChanges * 2LL;}
};js
/*** @param {number[]} nums* @param {number} k* @param {number} maxChanges* @return {number}*/
var minimumMoves = function(nums, k, maxChanges) {let c = 0;let pos = [];for (let i = 0; i < nums.length; i ++ ) {if (nums[i] == 0) continue;pos.push(i);c = Math.max(c, 1);if (i && nums[i - 1]) {if (i > 1 && nums[i - 2])c = 3;c = Math.max(c, 2);}}c = Math.min(c, k);if (maxChanges >= k - c)return Math.max(c - 1, 0) + (k - c) * 2;let n = pos.length;let acc = new Array(n + 1).fill(0);for (let i = 0; i < n; i ++ )acc[i + 1] = pos[i] + acc[i];let res = Infinity, sz = k - maxChanges;for (let r = sz; r <= n; r ++ ) {let l = r - sz, mid = l + parseInt(sz / 2);let s1 = pos[mid] * (mid - l) - (acc[mid] - acc[l]);let s2 = acc[r] - acc[mid] - pos[mid] * (r - mid);res = Math.min(res, s1 + s2);}return res + maxChanges * 2;
};相关文章:

中位数贪心,3086. 拾起 K 个 1 需要的最少行动次数
一、题目 1、题目描述 给你一个下标从 0 开始的二进制数组 nums,其长度为 n ;另给你一个 正整数 k 以及一个 非负整数 maxChanges 。 Alice 在玩一个游戏,游戏的目标是让 Alice 使用 最少 数量的 行动 次数从 nums 中拾起 k 个 1 。游戏开始…...

xml_woarchive undefined symbol
最近在linux中编译一个自己写的老代码。是个C动态库。可以编译成功,但直到运行的时候才报 boost xml_woarchive undefined symbol. 解决的方法是在编译时要加上 wserialization 库。 注意,这个库有含 w 和不含 w 两个。在我这里需要使用含 w 的。 如果…...

SiCat:一款多功能漏洞利用管理与搜索工具
关于SiCat SiCat是一款多功能漏洞利用管理与搜索工具,该工具基于纯Python 3开发,旨在帮助广大研究人员有效地识别和收集来自开源和本地存储库的漏洞信息。 SiCat专注于网络安全管理方面的实践工作,允许研究人员快速实现在线搜索,…...

毕业论文初稿写作方法与过程
毕业论文初稿写作方法与过程 毕业论文是大学生在学业结束前必须完成的一项重要任务,它不仅是对学生所学知识的综合运用,也是对学生研究能力和写作能力的检验。写好毕业论文初稿是完成高质量毕业论文的关键一步。下面将具体阐述毕业论文初稿的写作方法和过…...

SLAM 精度评估
SLAM 精度的评估有两个最重要的指标,即绝对轨迹误差(ATE)和相对位姿误差(RPE)的 均方根误差(RMSE): 绝对轨迹误差:直接计算相机位姿的真实值与 SLAM 系统的估计值之间的差值,首先将…...
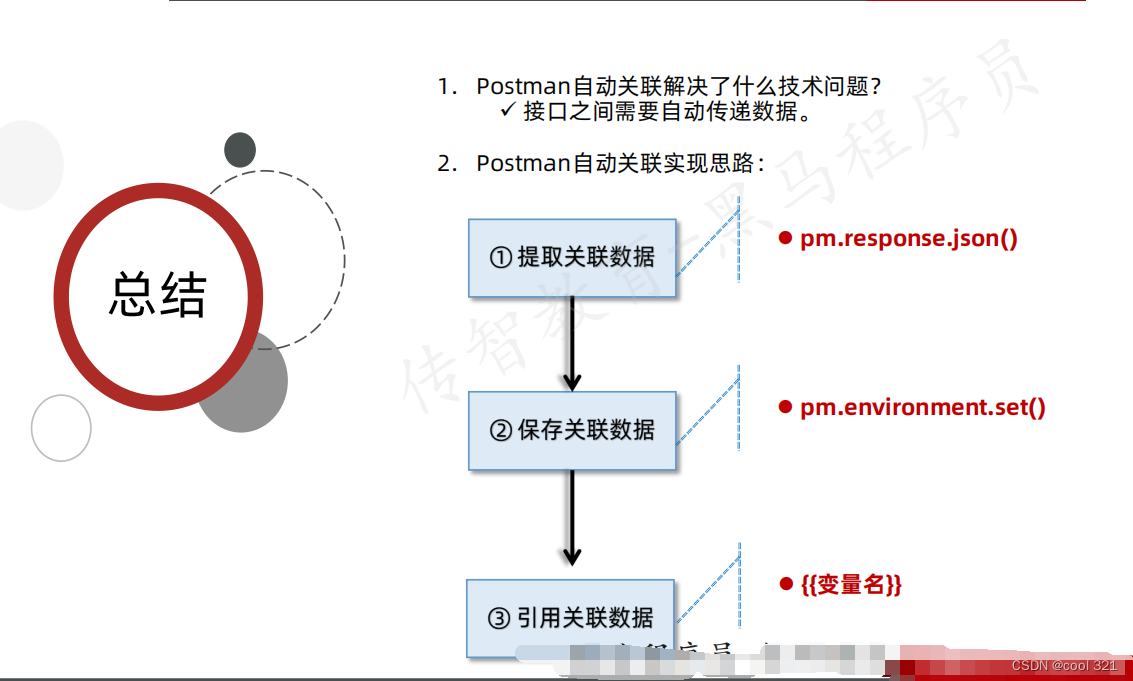
Postman使用教程
传统接口风格 RESTful风格 使用Postman完成测试用例目标: Postman教程 (1)准备工作,下载Postman新建 (2)登录接口调试-获取验证码 (3)登录接口调试-登录 (4)…...

UDP协议深入解析
一. UDP报文结构 UDP报文由以下4个字段组成: 源端口号(Source Port):16位,标识发送方的端口号。如果发送方没有使用端口号,则该字段为0。 目标端口号(Destination Port):16位,标识接收方的端口号。 长度(Length):16位,表示UDP报文的总长度,…...

Rethinking Federated Learning with Domain Shift: A Prototype View
CVPR2023,针对分布式数据来自不同的域时,私有模型在其他域上表现出退化性能(具有域转移)的问题。提出用于域转移下联邦学习的联邦原型学习(FPL)。核心思想是构建集群原型和无偏原型,提供富有成效的领域知识和公平的收敛目标。将样本嵌入拉近到属于相同语义的集群原型,而…...

打卡第2天----数组双指针,滑动窗口
今天是参与训练营第二天,这几道题我都看懂了,自己也能写出来了,实现思路很重要,万事开头难,希望我可以坚持下去。希望最后的结果是量变带来质变。 一、理解双指针思想 leetcode编号:977 不止是在卡尔这里…...

Running cmake version 2.8.12.2解决方案
Centos7安装mysql8.0,编译环节出现如下报错: Running cmake version 2.8.12.2 CMake Warning at CMakeLists.txt:82 (MESSAGE):Please use cmake3 rather than cmake on this platform-- Please install cmake3 (yum install cmake3) CMake Error at CMa…...
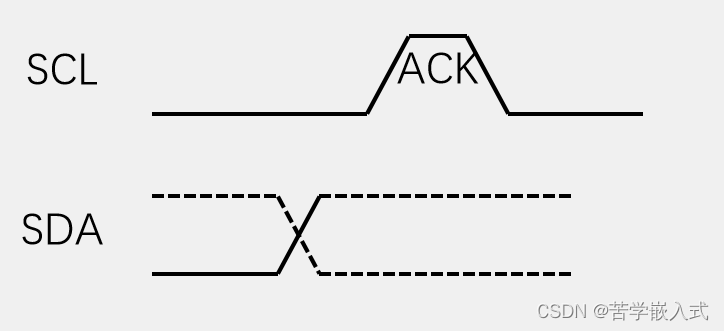
stm32中IIC通讯协议
参考资料:大部分均引用b站江协科技课程、GPT及网络资料 什么是IIC(i2C)通讯协议? 关键字:SCL、SDA、半双工、同步、串行。 IIC(Inter-Integrated Circuit),也称为I2C(In…...
那些年因为连接失败而一起熬过的夜)
允许防火墙通过端口 6379(通常用于 Redis 服务)那些年因为连接失败而一起熬过的夜
要允许防火墙通过端口 6379(通常用于 Redis 服务),您可以按照以下步骤在防火墙中添加规则。这里提供了使用 firewalld 和 ufw 两种常见防火墙管理工具的方法。 使用 firewalld (CentOS、Red Hat 等) 1. 启动并启用 f…...

tsconfig.json的include和exclude作用
tsconfig.json中的include和exclude属性用于指定需要被编译的TypeScript文件和需要被排除的文件。 include属性:用于指定哪些.ts、.tsx或.d.ts文件需要被编译。如果不指定include属性,则默认当前目录下除了exclude之外的所有.ts、.d.ts、…...

firewalld(8) policies
简介 前面的文章中我们介绍了firewalld的一些基本配置以及NAT的相关配置。在前面的配置中,我们所有的策略都是与zone相关的,例如配置的rich rule,--direct,以及NAT,并且这些配置都是数据包进入zone或者从zone发出时设置的策略。 我们在介绍…...

为什么进口主食冻干那么高贵?必入榜主食冻干总结分享
新手养猫人常常会有这样的疑问:为何进口主食冻干价格如此昂贵,但仍有大量养猫达人对其推崇备至?与国产主食冻干相比,进口产品的价格高出3-4倍之多,那么这高昂的价格背后,进口主食冻干是否真的值得推荐&…...

状态模式在金融业务中的应用及其框架实现
引言 状态模式(State Pattern)是一种行为设计模式,它允许对象在内部状态改变时改变其行为。状态模式通过将状态的相关行为分离到独立的状态类中,使得状态转换更加明确和简洁。在金融业务中,状态模式可以用于实现交易状…...
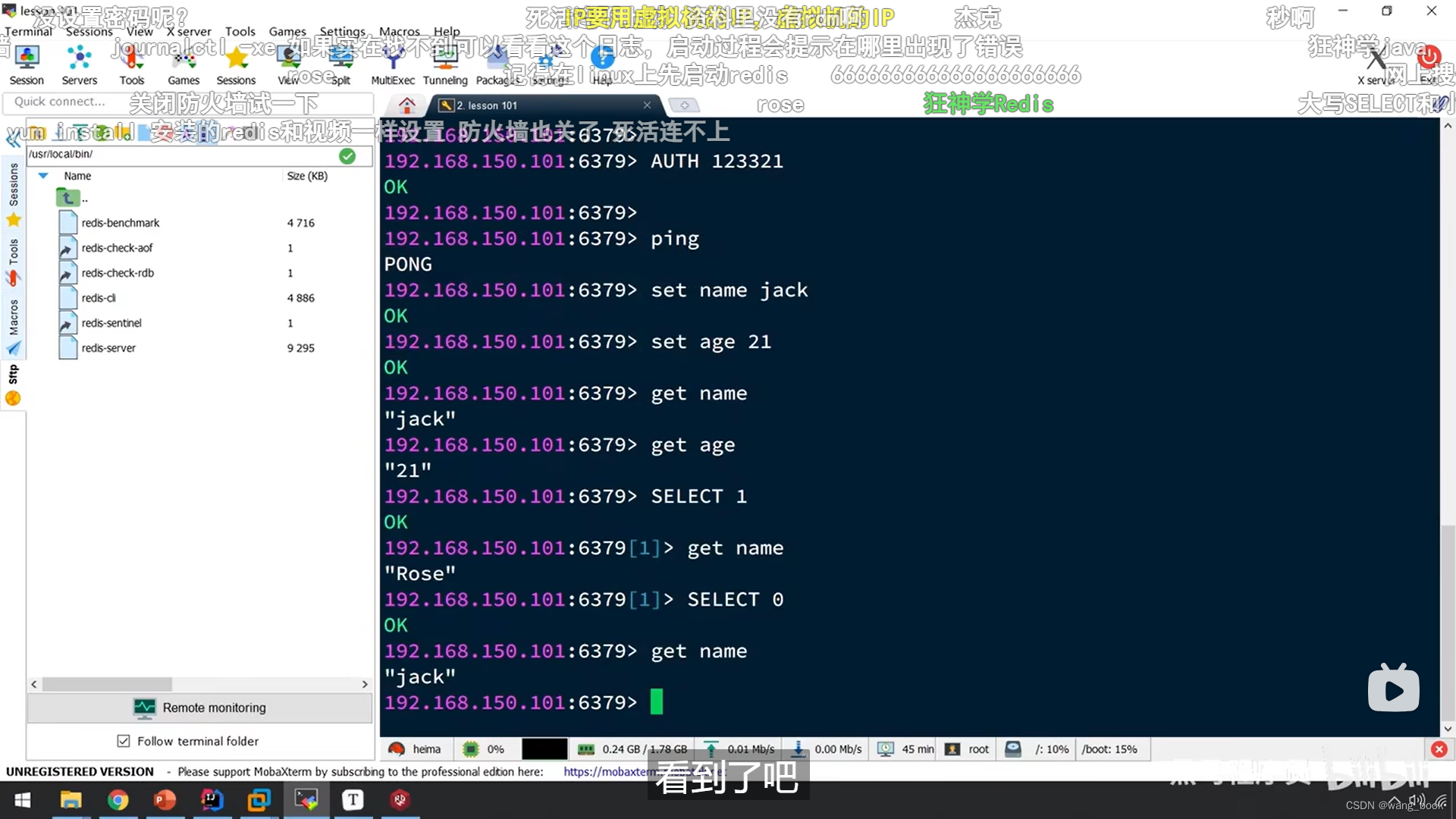
redis学习(002 安装redis和客户端)
黑马程序员Redis入门到实战教程,深度透析redis底层原理redis分布式锁企业解决方案黑马点评实战项目 总时长 42:48:00 共175P 此文章包含第5p-第p7的内容 文章目录 安装redis启动启动方式1:可执行文件启动启动方式2 基于配置文件启动修改redis配置文件 …...

在线客服系统多国语言,适合跨境外贸业务对外沟通 ,哈萨克语客服系统,根据浏览器语种标识自动切换...
我们看一下我们客服系统的哈萨克语展示。 演示网站:gofly.v1kf.com 有个客户,他们的业务主要是位于哈萨克斯坦,需求是访客端使用哈萨克语来展示。 现在这个界面就是哈萨克语的。当然,也可以切换成中文。界面上的文案已经切换成中文…...

等保2.0是否强制要求所有物联网设备都必须支持自动更新?
等保2.0对物联网设备自动更新的要求 等保2.0(网络安全等级保护2.0)是中国政府为了加强网络安全而推出的一套标准和要求。在物联网设备的安全管理方面,等保2.0确实提出了一系列措施,以确保设备的软件安全更新。这些措施包括&#…...

gin框架解决跨域问题
文章目录 前言一、使用github.com/gin-contrib/cors 前言 今天遇到了前后端跨域问题,前后端跨域解决蛮简单的,下面是解决方案 一、使用github.com/gin-contrib/cors go get github.com/gin-contrib/cors在路由的地方 r : gin.Default()corsConfig : c…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
