Docker 安装 Python
Docker 安装 Python
在当今的软件开发领域,Docker 已成为一项关键技术,它允许开发人员将应用程序及其依赖环境打包到一个可移植的容器中。Python,作为一种广泛使用的高级编程语言,经常被部署在 Docker 容器中。本文将详细介绍如何在 Docker 中安装 Python,以及如何配置环境以确保 Python 应用程序可以在 Docker 容器中顺利运行。
什么是 Docker?
Docker 是一个开源的平台,用于开发、运输和运行应用程序。Docker 使您能够将应用程序与基础设施分开,从而可以快速交付软件。使用 Docker,您可以像管理应用程序一样管理基础设施。通过利用 Docker 的方法进行快速交付、测试和部署代码,您可以显著缩短编写代码和在生产环境中运行代码之间的周期。
为什么在 Docker 中安装 Python?
在 Docker 中安装 Python 有多个好处:
- 环境隔离:Docker 提供了一个隔离的环境,这意味着您可以在不影响主机系统的情况下运行 Python 应用程序。
- 可移植性:Docker 容器可以在任何支持 Docker 的平台上运行,这确保了您的 Python 应用程序可以在不同的环境中无缝迁移。
- 一致性:Docker 确保了开发、测试和生产环境之间的一致性,减少了“在我的机器上可以运行”的问题。
- 资源效率:与虚拟机相比,Docker 容器占用的资源更少,启动速度更快。
在 Docker 中安装 Python 的步骤
1. 安装 Docker
在开始之前&#
相关文章:

Docker 安装 Python
Docker 安装 Python 在当今的软件开发领域,Docker 已成为一项关键技术,它允许开发人员将应用程序及其依赖环境打包到一个可移植的容器中。Python,作为一种广泛使用的高级编程语言,经常被部署在 Docker 容器中。本文将详细介绍如何在 Docker 中安装 Python,以及如何配置环…...
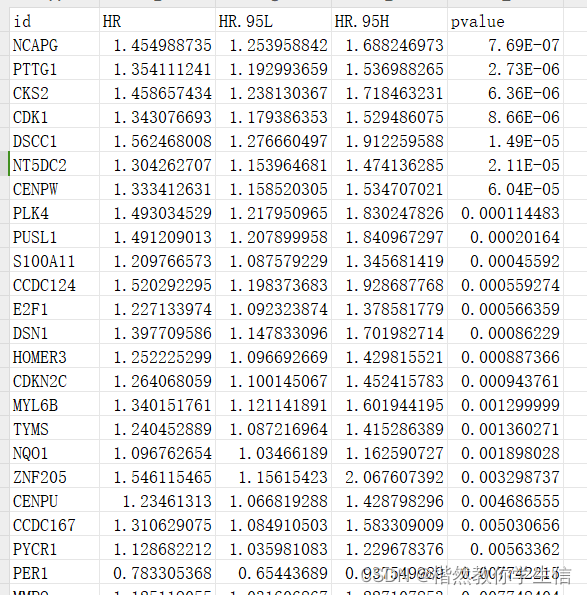
外泌体相关基因肝癌临床模型预测——2-3分纯生信文章复现——4.预后相关外泌体基因确定单因素cox回归(2)
内容如下: 1.外泌体和肝癌TCGA数据下载 2.数据格式整理 3.差异表达基因筛选 4.预后相关外泌体基因确定 5.拷贝数变异及突变图谱 6.外泌体基因功能注释 7.LASSO回归筛选外泌体预后模型 8.预后模型验证 9.预后模型鲁棒性分析 10.独立预后因素分析及与临床的…...

C++: Map数组的遍历
在C中,map是一个关联容器,它存储的元素是键值对(key-value pairs),其中每个键都是唯一的,并且自动根据键来排序。遍历map的方式有几种,但最常用的两种是使用迭代器(iterator…...

【Windows】Bootstrap Studio(网页设计)软件介绍及安装步骤
软件介绍 Bootstrap Studio 是一款专为前端开发者设计的强大工具,主要用于快速创建现代化的响应式网页和网站。以下是它的主要特点和功能: 直观的界面设计 Bootstrap Studio 提供了直观的用户界面,使用户能够轻松拖放元素来构建网页。界面…...

二维舵机颜色追踪,使用树莓派+opencv+usb摄像头+两个舵机实现颜色追踪,采用pid调控
效果演示 二维云台颜色追踪 使用树莓派opencvusb摄像头两个舵机实现颜色追踪,采用pid调控 import cv2 import time import numpy as np from threading import Thread from servo import Servo from pid import PID# 初始化伺服电机 pan Servo(pin19) tilt Serv…...

c进阶篇(四):内存函数
内存函数以字节为单位更改 1.memcpy memcpy 是 C/C 中的一个标准库函数,用于内存拷贝操作。它的原型通常定义在 <cstring> 头文件中,其作用是将一块内存中的数据复制到另一块内存中。 函数原型:void *memcpy(void *dest, const void…...

新手入门:无服务器函数和FaaS简介
无服务器(Serverless)架构的价值在于其成本效益、弹性和扩展性、简化的开发和部署流程、高可用性和可靠性以及使开发者能够专注于业务逻辑。通过自动化资源调配和按需计费,无服务器架构能够降低成本并适应流量变化,同时简化开发流…...

基于Transformer的端到端的目标检测 | 读论文
本文正在参加 人工智能创作者扶持计划 提及到计算机视觉的目标检测,我们一般会最先想到卷积神经网络(CNN),因为这算是目标检测领域的开山之作了,在很长的一段时间里人们都折服于卷积神经网络在图像处理领域的优势&…...
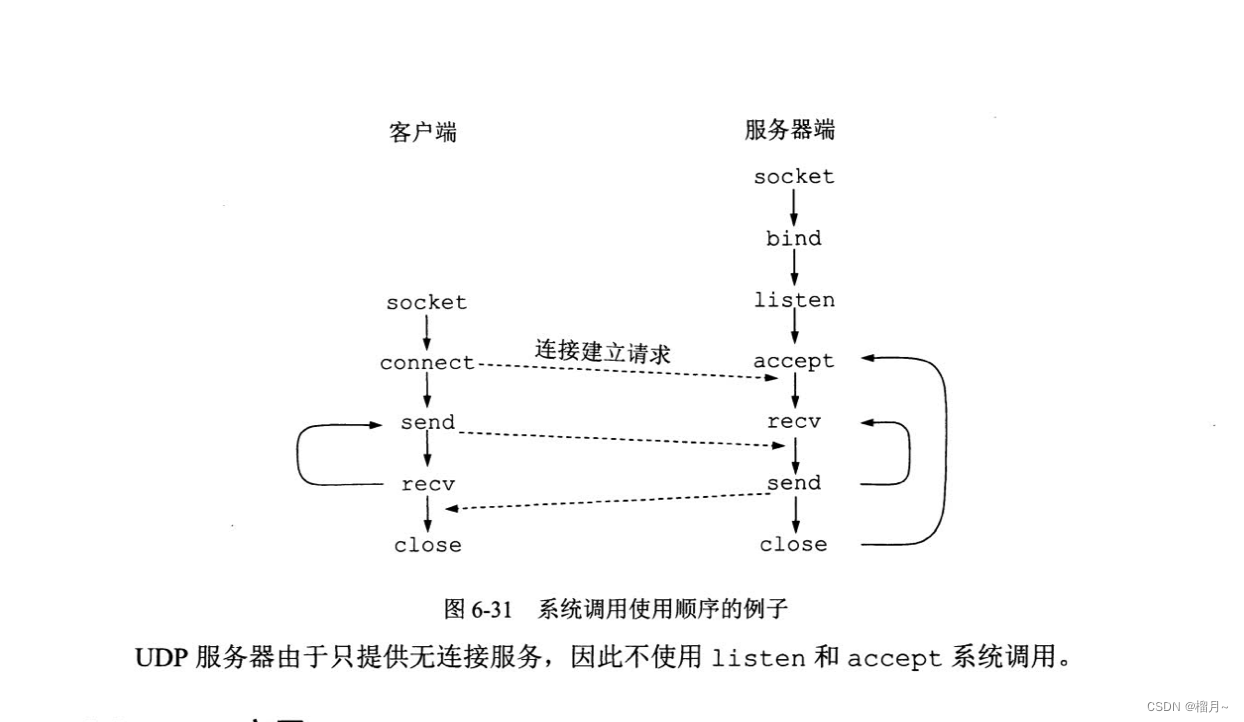
6.8应用进程跨网络通信
《计算机网络》第7版,谢希仁 理解socket通信...

redis布隆过滤器原理及应用场景
目录 原理 应用场景 优点 缺点 布隆过滤器(Bloom Filter)是一种空间效率很高的随机数据结构,它利用位数组和哈希函数来判断一个元素是否存在于集合中。 原理 数据结构: 位数组:一个由0和1组成的数组,初始…...
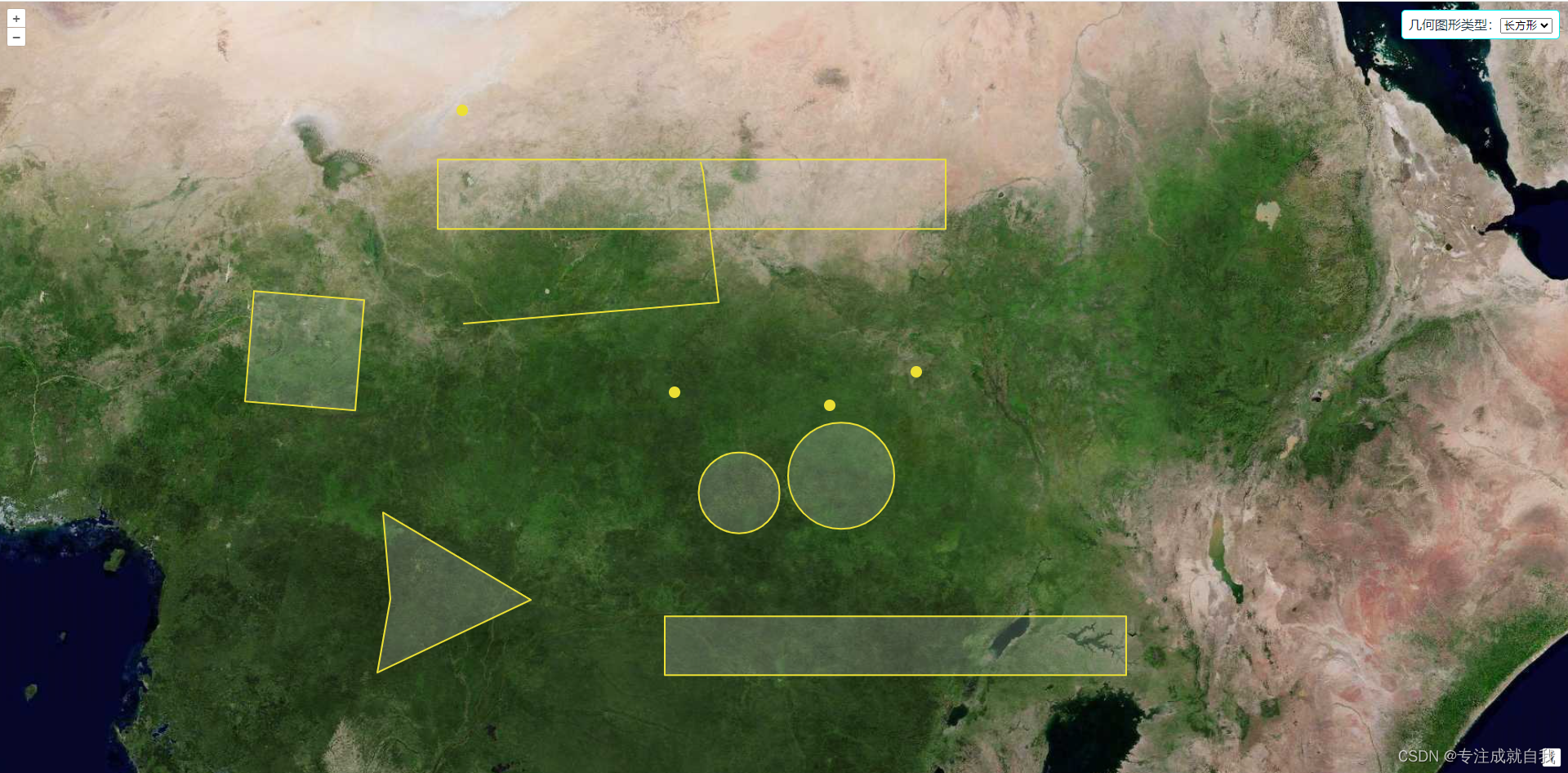
vue+openlayers之几何图形交互绘制基础与实践
文章目录 1.实现效果2.实现步骤3.示例页面代码3.基本几何图形绘制的关键代码 1.实现效果 绘制点、线、多边形、圆、正方形、长方形 2.实现步骤 引用openlayers开发库。加载天地图wmts瓦片地图。在页面上添加几何图形绘制的功能按钮,使用下拉列表(sel…...

「多模态大模型」解读 | 突破单一文本模态局限
编者按:理想状况下,世界上的万事万物都能以文字的形式呈现,如此一来,我们似乎仅凭大语言模型(LLMs)就能完成所有任务。然而,理想很丰满,现实很骨感——数据形态远不止文字一种&#…...

Redis深度解析:核心数据类型与键操作全攻略
文章目录 前言redis数据类型string1. 设置单个字符串数据2.设置多个字符串类型的数据3.字符串拼接值4.根据键获取字符串的值5.根据多个键获取多个值6.自增自减7.获取字符串的长度8.比特流操作key操作a.查找键b.设置键值的过期时间c.查看键的有效期d.设置key的有效期e.判断键是否…...
C语言 指针和数组——指针的算术运算
目录 指针的算术运算 指针加上一个整数 指针减去一个整数 指针相减 指针的关系比较运算 小结 指针的算术运算 指针加上一个整数 指针减去一个整数 指针相减 指针的关系比较运算 小结 指针变量 – 指针类型的变量,保存地址型数据 指针变量与其他类型…...

[C++][CMake][CMake基础]详细讲解
目录 1.CMake简介2.大小写?3.注释1.注释行2.注释块 4.日志 1.CMake简介 CMake是一个项目构建工具,并且是跨平台的 问题 – 解决 如果自己动手写Makefile,会发现,Makefile通常依赖于当前的编译平台,而且编写Makefile的…...

CCD技术指标
CCD尺寸,即摄象机靶面。原多为1/2英寸,现在1/3英寸的已普及化,1/4英寸和1/5英寸也已商品化。CCD像素,是决定了显示图像的清晰程度,。CCD是由面阵感光元素组成,每一个元素称为像素,像素越多&…...
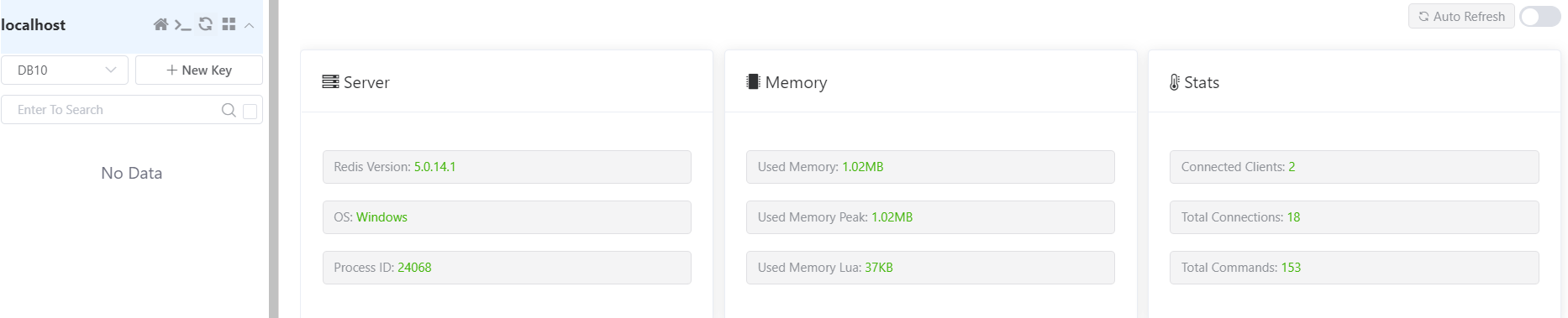
SpringBoot系列——使用Spring Cache和Redis实现查询数据缓存
文章目录 1. 前言2. 缓存2.1 什么是缓存2.2 使用缓存的好处2.3 缓存的成本2.4 Spring Cache和Redis的优点 3. Spring Cache基础知识3.1 Spring Cache的核心概念3.2 Spring Cache的注解3.2.1 SpEL表达式3.2.2 Cacheable3.2.3 CachePut3.2.4 CacheEvict 4. 实现查询数据缓存4.1 准…...

【算法】(C语言):冒泡排序、选择排序、插入排序
冒泡排序 从第一个数据开始到第n-1个数据,依次和后面一个数据两两比较,数值小的在前。最终,最后一个数据(第n个数据)为最大值。从第一个数据开始到第n-2个数据,依次和后面一个数据两两比较,数值…...

iOS项目怎样进行二进制重排
什么是二进制重排 ? 在iOS项目中,二进制重排(Binary Reordering 或者 Binary Rearrangement)是一种优化技术,主要目的是通过重新组织应用程序的二进制文件中的代码和数据段,来提高应用程序的性能ÿ…...
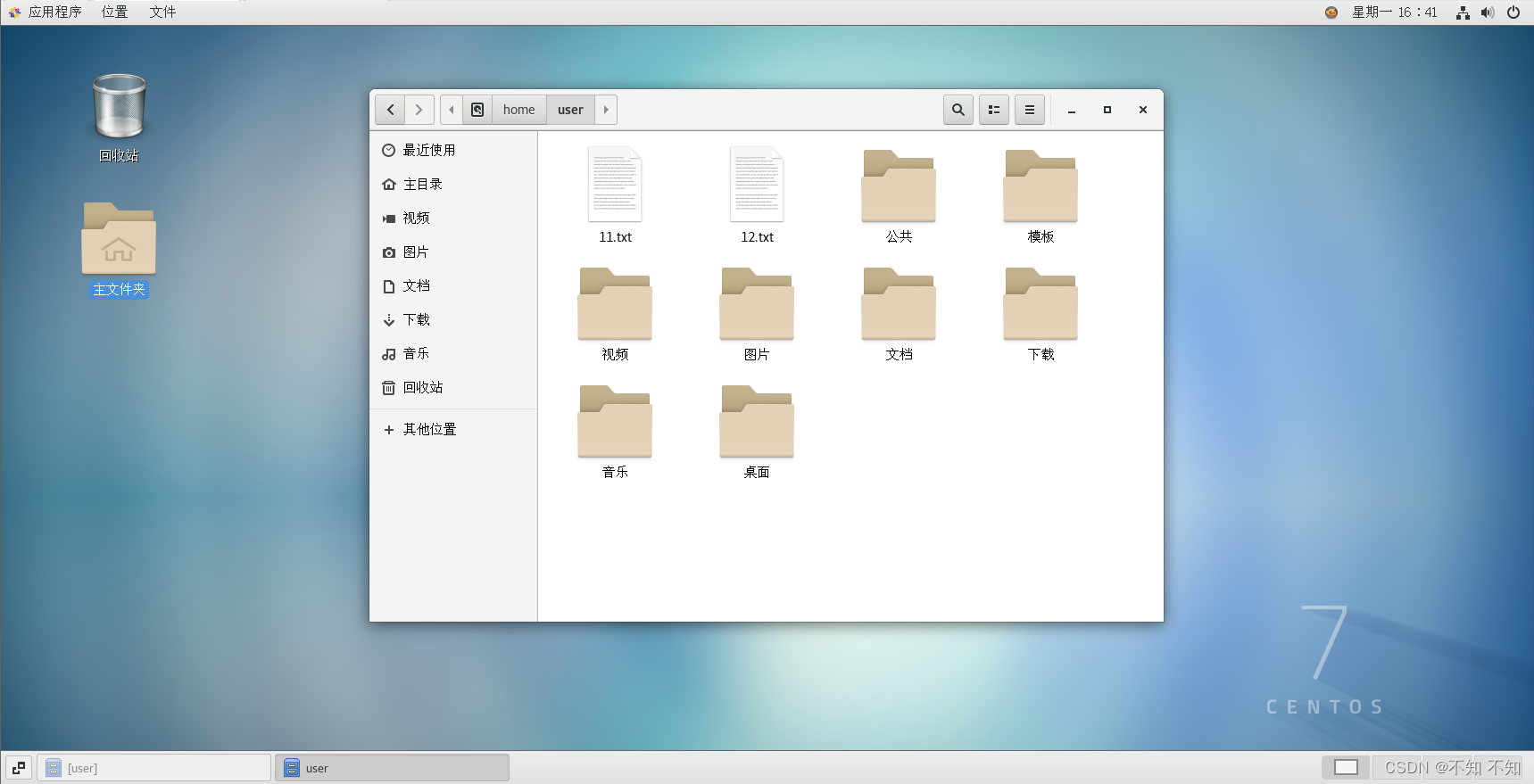
CentOS中使用SSH远程登录
CentOS中使用SSH远程登录 准备工作SSH概述SSH服务的安装与启动建立SSH连接SSH配置文件修改SSH默认端口SSH文件传输 准备工作 两台安装CentOS系统的虚拟机 客户机(192.168.239.128) 服务器(192.168.239.129) SSH概述 Secure S…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
