【密码学】RSA公钥加密算法
文章目录
- RSA定义
- RSA加密与解密
- 加密
- 解密
- 生成密钥对
- 一个例子
- 密钥对生成
- 加密
- 解密
- 对RSA的攻击
- 通过密文来求得明文
- 通过暴力破解来找出D
- 通过E和N求出D
- 对N进行质因数分解
- 通过推测p和q进行攻击
- 中间人攻击
- 一些思考
- 公钥密码比对称密码的机密性更高?
- 对称密码会消失?
- RSA使用过程中,质数对会不会被用光?
- RSA加密过程中需要对大整数进行质因数分解?
- N达到多少比特可以抵御质因数分解?
RSA定义
- RSA是一种公钥密码算法
- 他的名字由他的三位开发者的形式首字母组成
RSA加密与解密

加密
-
密文 = 明文EmodN
-
在RSA只能够,明文、密钥和密文都是数字,具体加密过程可由上式来表达,RSA的密文就是对代表明文的数字的E次方求modN的结果
-
E和N的组合就是密钥,一般可写成“密钥是(E, N)”
解密
- 明文 = 密文DmodN
- 对表示密文 数字的D次方求modN就可以得到明文
- D和N的组合就是私钥,一般可写成“私钥是(D, N)”,这里所使用的数字N和加密时使用的数字N是相同的
生成密钥对
- 公钥是(E, N),私钥是(D, N),因此求E, D, N这三个数的过程就是生成密钥对的过程,即为RSA密钥对的生成过程
- 求N
- 首先准备两个很大的质数p, q
- 若p和q过小的话,密码会变得容易破译;但若p和q过大的话计算时间又会变得很长
- N为两质数的乘积
- N = p*q
- 求L
- L是(p-1)和(q-1)的最小公倍数(least common multiple),用lcm(X, Y)来表示“X和Y的最小公倍数”
- L = lcm(p-1, q-1)
- 求E
- E是一个比1大、比L小的数
- E和L的最大公约数(greatest common divisor)必须是1,用gcd(X, Y)来表示X和Y的最大公约数
- 1 < E < L, gcd(E, L) = 1
- 要找到满足要求的数,要使用伪随机数生成器,通过伪随机数生成器在1 < E < L的范围内生成E的候选数,然后再判断其是否满足gcd(E, L) = 1这个条件
- 求D
- 1 < D < L, E * D mod L = 1
- 只要数D满足上述条件,则通过E和N进行加密的密文,就可以通过D和N进行解密
一个例子
密钥对生成
- 求N
- p = 17, q = 19
- N = p * q = 17 * 19 = 323
- 求L
- L = lcm(p-1, q-1) = lcm(16, 18) = 144
- 求E
- gcd(E, L) = 1
- E = 5、7、11、13、17…
- 选取E = 5,N = 323
- 求D
- E * D mod L = 1
- 将D = 29代入上式即满足
- E * D mod L = 5 * 29 mod 144 = 145 mo 144 = 1
- 得公钥(E, N) = (5, 323),私钥(D, N) = (29, 323)
- 公钥是可以任意公开的,但私钥必须妥善保管
加密
- 要加密的明文必须是小于N的数,即此处必须是小于323的数,因为在加密过程中有mod N操作
- 假设需要加密的数是123,公钥(E, N) = (5, 323)
- 密文 = 明文Emod N = 1235mod 323 = 225
解密
- 收到密文是225,私钥(D, N) = (29, 323)
- 明文 = 密文Dmod N = 22529mod 323 = 123
对RSA的攻击
- 密码破译者知道的信息
- 密文:可以通过窃听来获取
- 公钥(E, N):公钥是公开信息
- 密码破译者不知道的信息
- 明文:需要破译的内容
- 私钥中的D:私钥中的D是不知道的
- 其他:密码破译者不知道生成密钥对时所使用的p、q、L
通过密文来求得明文
- 若在加密过程中,没有mod N的操作,通过密文求解明文的难度并不大,因为可以看作是一个求对数的问题
- 但是,加上mod N后,求明文就变成了求离散对数的问题,这种操作非常困难,目前还没有发现求解离散对数的高效算法
通过暴力破解来找出D
- 只要能知道D,就能对密文进行解密。因此可以逐一尝试有可能作为D的数字来破译RSA,即暴力破解法
- 暴力破解法的难度会随着D的长度增大而增大,当D足够长时,就不可能在现实的时间内通过暴力破解找出D
- 现在RSA所使用的p和q的长度都是1024比特以上的,N的长度为2048比特以上的,由于E和D的长度可以和N差不多,因此要找出D,就需要进行2048比特以上的暴力破解
通过E和N求出D
对N进行质因数分解
- p和q是不能被密码破译者知道的,因为N = p * q,而且N是公开的,p和q都是质数,因此由N求p和q只能通过将N进行质因数分解来完成
- 一旦发现了对大整数进行质因数分解的高效算法,RSA就能够被破译
- 然而,现在还没有发现对大整数进行质因数分解的高效算法,而且也尚未证明质因数分解是否真的是非常困难的问题,甚至不知道是否存在一种分解质因数的简单方法
通过推测p和q进行攻击
- 由于p和q是通过伪随机数生成器产生的,如果伪随机数生成器的算法很差,密码破译者就有可能推测出来p和q,因此使用能够被推测出来的随机数是非常危险的
中间人攻击
- man-in-the-middle attack
- 这种方法虽不能破译RSA,但却是一种针对机密性的有效攻击
- 中间人攻击就是主动攻击者M混入发送者和接收者中间,对发送者伪装成接收者,对接收者伪装成发送者的攻击方式,此时M就是“中间人”

- 消息发送者A向B发送邮件索取公钥
- 攻击人M通过窃听发现A在向B索取公钥
- B看到A的邮件,并将自己的公钥发送给A
- M拦截B的邮件,使其无法发送给A,然后将B的公钥保存起来
- M伪装成B,将M自己的公钥发送给A
- A将自己的消息用B的公钥(此时其实是M的公钥)进行加密
- A将加密后的消息发送给B
- 但A所持有的并非B的公钥,而是M的公钥,因此A是用M的公钥对邮件进行加密
- M拦截A的加密邮件
- 这封加密邮件是用M的公钥进行加密的,因此M能够对其进行解密
- M伪装成A写一封假的邮件,并用4中保存下来的B的公钥对邮件进行加密,再发送给B
- 上述过程可以反复多次,B向A发送加密邮件也可能受到同样的攻击
- 中间人攻击可以针对任何公钥密码,攻击过程中,公钥密码并没有被破译,所有的密码算法也都正常工作并确保了机密性,然而所谓的机密性并不存在在A与B之间,而成立在A与M之间与M与B之间
- 仅靠公钥密码本身,是无法防御中间人攻击的,这种情况,可以使用公钥的证书
一些思考
公钥密码比对称密码的机密性更高?
- 不一定
- 机密性的高低是根据密钥长度而变化的
对称密码会消失?
- 不会
- 虽然有了公钥密码,但对称密码也不会消失
- 一般来说,在采用具备同等机密性的密钥长度的情况下,公钥密码的处理速度只有对称密码的几百分之一,因此公钥密码并不适合用来对很长的消息内容进行加密
- 根据目的的不同,还可能会配合使用对称密码和公钥密码
RSA使用过程中,质数对会不会被用光?
- 不会
- 512比特能够容纳的质数数量约为10的150次方,假设世界上有100亿人,每人每秒生成100亿个密钥对,那么在经过100亿年后会生成:100亿人 * 100亿个 * (366 * 24 * 60 * 60)秒 * 100亿年 = 316224 * 1032 < 1039 << 10150
RSA加密过程中需要对大整数进行质因数分解?
- 不需要
- RSA加密和解密的过程都无需对大整数进行质因数分解操作
- 只有在需要有数N求p和q的密码破译过程中才需要对大整数进行质因数分解,RSA的设计是将质因数分解的难题留给密码破译者
N达到多少比特可以抵御质因数分解?
- 不能抵御
- N无论有多长,总有一天能被质因数分解,因此问题是能否在现实的时间内对N进行质因数分解
相关文章:

【密码学】RSA公钥加密算法
文章目录 RSA定义RSA加密与解密加密解密 生成密钥对一个例子密钥对生成加密解密 对RSA的攻击通过密文来求得明文通过暴力破解来找出D通过E和N求出D对N进行质因数分解通过推测p和q进行攻击 中间人攻击 一些思考公钥密码比对称密码的机密性更高?对称密码会消失&#x…...

【ARMv8/v9 GIC 系列 5.1 -- GIC GICD_CTRL Enable 1 of N Wakeup Function】
请阅读【ARM GICv3/v4 实战学习 】 文章目录 GIC Enable 1 of N Wakeup Function基本原理工作机制配置方式应用场景小结GIC Enable 1 of N Wakeup Function 在ARM GICv3(Generic Interrupt Controller第三代)规范中,引入了一个名为"Enable 1 of N Wakeup"的功能。…...

C++怎么解决不支持字符串枚举?
首先,有两种方法:使用命名空间和字符串常量与使用 enum class 和辅助函数。 表格直观展示 特性使用命名空间和字符串常量使用 enum class 和辅助函数类型安全性低 - 编译器无法检查字符串有效性,运行时发现错误高 - 编译期类型检查…...
)
中英双语介绍四大会计师事务所(Big Four accounting firms)
中文版 “四大会计师事务所”(Big Four accounting firms)是全球最具影响力和规模最大的四家专业服务公司,它们在审计、税务、咨询和财务咨询等领域占据着主导地位。这四家公司分别是普华永道(PwC)、德勤(…...

ubuntu 查看联网配置
在Ubuntu中,你可以使用多种命令来查看联网配置。以下是一些常用的方法和命令: 查看网络接口配置: 使用 ip 命令可以查看网络接口的配置信息,包括IP地址、子网掩码等。 ip addr show或者,你也可以使用传统的 ifconfig 命…...

【数据分享】全国乡村旅游重点镇(乡)数据(Excel/Shp格式/免费获取)
之前我们分享过从我国文化和旅游部官网整理的2018-2023年我国50个重点旅游城市星级饭店季度经营状况数据(可查看之前发布的文章)!文化和旅游部官网上也分享有很多与旅游相关的常用数据,我们基于官网发布的名单文件整理得到全国乡村…...

停车场小程序的设计
管理员账户功能包括:系统首页,个人中心,车主管理,商家管理,停车场信息管理,预约停车管理,商场收费管理,留言板管理 微信端账号功能包括:系统首页,停车场信息…...
绿色金融相关数据合集(2007-2024年 具体看数据类型)
数据类型: 1.绿色债券数据:2014-2023 2.绿色信贷相关数据:2007-2022 3.全国各省及地级市绿色金融指数:1990-2022 4.碳排放权交易明细数据:2013-2024 5.绿色金融试点DID数据:2010-2023 数据来源&#…...

【matlab 项目工期优化】基于NSGA2/3的项目工期多目标优化(时间-成本-质量-安全)
一 背景介绍 本文分享了一个通用的项目工期优化的案例,决策变量是每个子项目的工期,优化目标是项目的完成时间最小,项目的总成本现值最小,项目的总安全水平最高,项目的总质量水平最高。采用的算法是NSGA2和NSGA3算法。…...

Python考前复习
选择题易错: python3不能完全兼容python2内置函数是python的内置对象之一,无需导入其他模块python中汉字变量合法,如“小李123”合法;但T-C不合法,因为有“-”集合无顺序,不能索引;range(5)[2]…...

虚拟机交叉编译基于ARM平台的opencv(ffmpeg/x264)
背景: 由于手上有一块rk3568的开发板,需要运行yolov5跑深度学习模型,但是原有的opencv不能对x264格式的视频进行解码,这里就需要将ffmpegx264编译进opencv。 但是开发板算力有限,所以这里采用在windows下,安…...

react之错误边界
错误边界实质是指什么 实际上是组件 错误边界捕获什么时候的错误 在渲染阶段的错误 错误边界捕获的是谁的错误 捕获的是子组件的错误 错误边界不能捕获什么错误 1、不能捕获异步代码 2、不能捕获事件处理函数 3、不能捕获服务端渲染 4、不能捕获自身抛出的错误 错误…...

openEuler系统之使用Keepalived+Nginx部署高可用Web集群
Linux系统之使用Keepalived+Nginx部署高可用Web集群 一、本次实践介绍1.1 本次实践简介1.2 本次实践环境规划二、keepalived介绍2.1 keepalived简介2.2 keepalived主要特点和功能2.3 使用场景三、Keepalived和Nginx介绍3.1 Nginx简介3.2 Nginx特点四、master节点安装nginx4.1 安…...

基于图像处理的滑块验证码匹配技术
滑块验证码是一种常见的验证码形式,通过拖动滑块与背景图像中的缺口进行匹配,验证用户是否为真人。本文将详细介绍基于图像处理的滑块验证码匹配技术,并提供优化代码以提高滑块位置偏移量的准确度,尤其是在背景图滑块阴影较浅的情…...

【JavaEE精炼宝库】文件操作(1)——基本知识 | 操作文件——打开实用性编程的大门
目录 一、文件的基本知识1.1 文件的基本概念:1.2 树型结构组织和目录:1.3 文件路径(Path):1.4 二进制文件 VS 文本文件:1.5 其它: 二、Java 操作文件2.1 方法说明:2.2 使用演示&…...

常用排序算法_06_归并排序
1、基本思想 归并排序采用分治法 (Divide and Conquer) 的一个非常典型的应。归并排序的思想就是先递归分解数组,再合并数组。归并排序是一种稳定的排序方法。 将数组分解最小之后(数组中只有一个元素,数组有序);然后…...
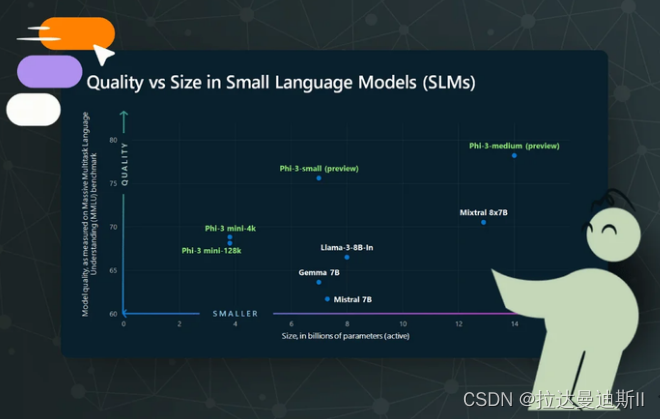
14-8 小型语言模型的兴起
过去几年,我们看到人工智能能力呈爆炸式增长,其中很大一部分是由大型语言模型 (LLM) 的进步推动的。GPT-3 等模型包含 1750 亿个参数,已经展示了生成类似人类的文本、回答问题、总结文档等能力。然而,虽然 LLM 的能力令人印象深刻…...

【Linux】:进程创建与终止
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux程序地址空间的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从…...

横截面交易策略:概念与示例
数量技术宅团队在CSDN学院推出了量化投资系列课程 欢迎有兴趣系统学习量化投资的同学,点击下方链接报名: 量化投资速成营(入门课程) Python股票量化投资 Python期货量化投资 Python数字货币量化投资 C语言CTP期货交易系统开…...

4.2 投影
一、投影和投影矩阵 我们以下面两个问题开始,问题一是为了展示投影是很容易视觉化的,问题二是关于 “投影矩阵”(projection matrices)—— 对称矩阵且 P 2 P P^2P P2P。 b \boldsymbol b b 的投影是 P b P\boldsymbol b Pb。…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
