调和均值
文章目录
- 调和均值的定义和公式
- 调和均值的几何解释
- 调和均值的应用
- 调和均值与算术平均和几何平均的比较
- 示例
调和均值的定义和公式
调和均值是一种特殊的平均数,适用于处理涉及比率或速度的数据。对于一组正数 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn,调和均值 H H H 的公式如下:
H = n 1 x 1 + 1 x 2 + ⋯ + 1 x n H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}} H=x11+x21+⋯+xn1n
其中, n n n 是数值的个数。
调和均值的几何解释
调和均值可以理解为一种“倒数的平均”的倒数。具体来说,如果对每个数值取倒数,计算这些倒数的算术平均,然后再取这个算术平均的倒数,就得到了调和均值。
调和均值的应用
调和均值在以下几种情况下特别有用:
-
平均速度:当涉及到不同速度的平均时,调和均值是正确的选择。例如,如果在一段旅程中以不同的速度行驶不同的距离,调和均值可以帮助计算整个旅程的平均速度。
-
金融和经济学:在计算投资回报率、利率或价格指数时,调和均值可以提供更准确的结果。
-
物理学:在处理涉及频率、周期或阻抗的问题时,调和均值是合适的工具。
调和均值与算术平均和几何平均的比较
-
算术平均:算术平均是最常见的平均数,适用于大多数情况。公式为:
算术平均 = x 1 + x 2 + ⋯ + x n n \text{算术平均} = \frac{x_1 + x_2 + \cdots + x_n}{n} 算术平均=nx1+x2+⋯+xn
-
几何平均:几何平均适用于处理乘法关系的数据,如增长率。公式为:
几何平均 = x 1 × x 2 × ⋯ × x n n \text{几何平均} = \sqrt[n]{x_1 \times x_2 \times \cdots \times x_n} 几何平均=nx1×x2×⋯×xn
-
调和均值:调和均值适用于处理涉及比率或速度的数据。公式如前所述。
示例
假设有两段旅程,第一段以 60 km/h 的速度行驶 100 km,第二段以 80 km/h 的速度行驶 100 km。整个旅程的平均速度不是简单的算术平均(即 60 + 80 2 = 70 \frac{60 + 80}{2} = 70 260+80=70 km/h),而是调和均值:
H = 2 1 60 + 1 80 = 2 4 240 + 3 240 = 2 7 240 = 2 × 240 7 ≈ 68.57 km/h H = \frac{2}{\frac{1}{60} + \frac{1}{80}} = \frac{2}{\frac{4}{240} + \frac{3}{240}} = \frac{2}{\frac{7}{240}} = \frac{2 \times 240}{7} \approx 68.57 \text{ km/h} H=601+8012=2404+24032=24072=72×240≈68.57 km/h
这个例子说明了调和均值在处理涉及速度的平均时的正确性和实用性。
相关文章:

调和均值
文章目录 调和均值的定义和公式调和均值的几何解释调和均值的应用调和均值与算术平均和几何平均的比较示例 调和均值的定义和公式 调和均值是一种特殊的平均数,适用于处理涉及比率或速度的数据。对于一组正数 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2…...

DP学习——模板模式
学而时习之,温故而知新。 字面理解 模板?啥叫模板?模板就是固定死了,就是一套流程/步骤上层写死了。固定死了的流程或者步骤就是模板。然后我们要重写或者改写的是写死的这套流程中的节点。俗称“套模板”。 使用场合ÿ…...

AOP在业务中的简单使用
背景 业务组有一些给开发用的后门接口,为了做到调用溯源,业务组最近需要记录所有接口的访问记录,暂时只需要记录接口的响应结果,如果调用失败,则记录异常信息。由于后门接口较多以及只是业务组内部轻度使用࿰…...

C# 用户权限界面的测试内容
测试用户权限界面的主要目标是确保权限管理功能按照设计工作,同时保证用户界面响应正确,不会出现意外的行为或安全漏洞。以下是C#中用户权限界面测试的一些关键内容: 1. 功能性测试 权限分配与撤销:测试权限的分配和撤销功能&am…...

PyCharm
一、介绍 PyCharm 是 JetBrains 公司开发的一款功能强大的 Python 集成开发环境(IDE)。它专为 Python 开发设计,提供了一系列强大的工具和功能,帮助开发者更高效地编写、调试和维护 Python 代码。以下是对 PyCharm 的详细介绍&am…...

【嵌入式开发 Linux 常用命令系列 1.5 -- grep 过滤特定类型文件】
请阅读【嵌入式开发学习必备专栏 】 文章目录 grep 过滤特定类型文件 grep 过滤特定类型文件 在Linux中使用grep搜索字符串时,如果你想排除特定类型的文件,比如 .map 和 .py 文件,可以使用grep的--exclude选项。这个选项允许你定义一个或多个…...
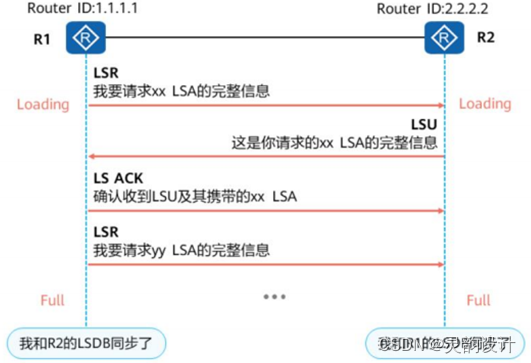
学习笔记——动态路由——OSPF(邻接/邻居)
十、OSPF的邻接/邻居 1、OSPF路由器之间的关系 (1)基本介绍 在OSPF网络中,为了交换链路状态信息和路由信息,邻居设备之间首先要建立邻接关系,邻居(Neighbors)关系和邻接(Adjacencies)关系是两个不同的概念。 OSPF路由器的两种关系&#x…...

k8s 答疑
1 如何修复容器中的 top 指令以及 /proc 文件系统中的信息呢? 这段自问自答的内容解释了如何通过使用 lxcfs 来修复 Docker 容器中 top 指令和 /proc 文件系统中的信息。让我们分步骤来详细说明: 背景信息 在容器化环境中,通常会遇到一个问题,即容器中的一些命令(如 to…...
)
[终端安全]-2 移动终端之硬件安全(SE)
本文主要介绍针对安全芯片的攻击和防护方案。 1 芯片攻击 1)故障注入攻击 故障注入攻击(Fault Injection Attack, FIA)是一种通过人为引入故障,诱发系统或芯片在异常情况下产生错误结果,从而泄露机密信息或破坏系统…...

数据库与SQL
数据库基本概念 数据库(DataBase):数据库就是存储数据的仓库数据库管理系统(DBMS):可以独立运行的软件,维护磁盘上的数据,用统一的方式维护不同种类的数据,做到通用且高效。常见的DBMS: mysqloracledb2sqlserver 数据…...

AIGC | 在机器学习工作站安装NVIDIA CUDA® 并行计算平台和编程模型
[ 知识是人生的灯塔,只有不断学习,才能照亮前行的道路 ] 0x02.初识与安装 CUDA 并行计算平台和编程模型 什么是 CUDA? CUDA(Compute Unified Device Architecture)是英伟达(NVIDIA)推出的并行计算平台和编…...

【电商纯干货分享】干货速看!电商数据集数据API接口数据分析大全!
数据分析——深入探索中小企业数字化转型,专注提供各行业数据分析干货、分析技巧、工具推荐以及各类超实用分析模板,为钻研于数据分析的朋友们加油充电。 公共参数 名称类型必须描述keyString是调用key(必须以GET方式拼接在URL中)…...

随手记录: Ubuntu NVIDIA显卡驱动安装后 屏幕亮度无法调节 无法连接外显示器等问题
背景 一句话:简单记录帮身边人装系统发现 GPU和外接显示器的无法连接,同时亮度无法调节等新问题 设备型号: 联想笔记本:ThinkBook 16p Gen2CPU:AMD Ryzen 7 5800HGPU:RTX 3060 问题描述及流程ÿ…...

Java:数组
文章目录 一、概念二、声明数组2.1 格式2.2 实例 三、初始化数组3.1 格式3.2 实例 四、处理数组4.1 for循环4.2 增强for循环 五、多维数组5.1 格式5.2 实例 一、概念 数组对于每一门编程语言来说都是重要的数据结构之一,当然不同语言对数组的实现及处理也不尽相同。…...

【代码随想录——图论——岛屿问题】
1.岛屿数量 https://kamacoder.com/problempage.php?pid1171 1.1 深度优先搜索 package mainimport "fmt"var direction [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}func main() {var M, N intfmt.Scanln(&N, &M)sea : make([][]int, N)visited : make…...

异步调用 - 初识
目录 1、引入 2、同步调用 2.1、例子:支付功能 2.2、同步调用的好处 2.3、同步调用的缺点 3、异步调用 3.1、异步调用的方式 3.2、异步调用的优势 3.3、异步调用的缺点 3.4、什么场景下使用异步调用 3.5、MQ技术选型 1、引入 为什么想要异步通信呢&…...

Java 家庭物联网
家庭物联网系统的代码和说明,包括用户认证、设备控制、数据监控、通知和警报、日志记录以及WebSocket实时更新功能。 ### 项目结构 plaintext home-iot-system ├── backend │ └── src │ └── main │ └── java │ └…...
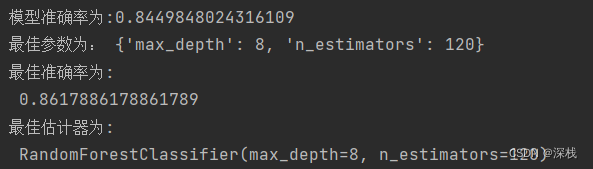
机器学习——随机森林
随机森林 1、集成学习方法 通过构造多个模型组合来解决单一的问题。它的原理是生成多个分类器/模型,各自独立的学习和做出预测。这些预测最后会结合成组合预测,因此优于任何一个单分类得到的预测。 2、什么是随机森林? 随机森林是一个包含…...

Java - JDK17语法新增特性(如果想知道Java - JDK17语法新增常见的特性的知识点,那么只看这一篇就足够了!)
前言:Java在2021年发布了最新的长期支持版本:JDK 17。这个版本引入了许多新的语法特性,提升了开发效率和代码可读性。本文将简要介绍一些常见的新特性,帮助开发者快速掌握并应用于实际开发中。 ✨✨✨这里是秋刀鱼不做梦的BLOG ✨…...

Linux-DNS
DNS域名解析服务 1.DNS介绍 DNS 是域名系统 (Domain Name System) 的缩写,是因特网的一项核心服务,它作为可以将域名和IP地址相互映射的一个分布式数据库,能够使人更方便的访问互联网,而不用去记住能够被机器直接读取的IP数串。…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
