【基于R语言群体遗传学】-4-统计建模与算法(statistical tests and algorithm)
之前的三篇博客,我们对于哈代温伯格遗传比例有了一个全面的认识,没有看的朋友可以先看一下前面的博客:
群体遗传学_tRNA做科研的博客-CSDN博客
1.一些新名词
(1)Algorithm: A series of operations executed in a specific order.
算法:按照特定顺序执行的一系列操作。
(2)Probability: The chance of an occurrence given repeated attempts.
概率:在重复尝试中发生的可能性。
(3)Likelihood: The chance of an occurrence given a model assumption.
可能性:在给定模型假设下发生的机会。
(4)Machine Learning: A process where computational results are validated to improve accuracy.
机器学习:验证计算结果以提高准确性的过程。
(5)Parthenogenesis: Development of an embryo without fertilization.
单性生殖:胚胎未经受精而发育。
(6)Autogamic: Self-fertilizing.
自花授粉:自我受精。
2.期望的偏差(Deviation from exception)
在这一点上,我们已经花费了大量时间来验证我们对哈代-温伯格假设下的等位基因频率的期望是否合理。我们可以做出的最有趣的观察之一是,某个种群正在违背我们的期望,当这种情况发生时,我们就可以开始探索其他可能性。在这个探索中,我们可以使用的一个特定的统计工具叫做χ2(卡方)统计检验。我们可以使用这个检验来看我们的观察到的基因型频率是否真的偏离了基于哈代-温伯格预测的期望。关于R语言统计相关的知识,可以看我写的博客:
【R语言从0到精通】-3-R统计分析(列联表、独立性检验、相关性检验、t检验)_r 列联表分析-CSDN博客
我们通过一个真实的数据集,该数据集包含了来自尼日利亚拉各斯501人样本的基因型计数(Taiwo等人,2011年)。这些是产生血红蛋白的基因的基因型,该基因与镰状细胞贫血症(血红蛋白S)相关。首先,我们计算等位基因和预期基因型频率,然后我们可以对这些数据进行χ2检验。 首先,将每个观察到的基因型计数保存为它们自己的变量。我们将使用AA表示纯合子非镰刀基因型,SS表示纯合子镰刀等位基因基因型,AS表示杂合子,三者的和就是总人数N。
| Genotyoe | AA | SS | AS |
| number | 366 | 12 | 123 |
我们计算镰刀型等位基因S的等位基因频率:
AA <- 366
AS <- 123
SS <- 12
N <- AA + AS + SS
p <- (SS + (AS/2))/N
p![]()
根据观察到的等位基因频率p,我们现在可以计算预期的基因型。因为我们想要追踪两种不同的等位基因(S和A),因此有两种不同的纯合性,我们将SS纯合子定义为p²,而AA纯合子定义为(1-p)²。这里的含义是,只有两种可能的等位基因:S的频率为p,A的频率为非p的所有部分。 现在,通过将我们计算出的基因型频率乘以实际抽样个体的数量,我们可以得到我们预期的个体基因型数量:
ExpAA <- N*(1-p)^2
ExpAS <- N*2*p*(1-p)
ExpSS <- N*p^2
为了确定我们所看到的基因型数量是否真的符合我们的预期,我们将使用内置的R函数pchisq()来计算来自χ²分布的概率值(P值)。在pchisq()函数中,我们希望将参数lower.tail设置为FALSE,因为我们想看到我们的χ²值高于实际值的概率。随着我们的观察和预期差异越来越大,我们的χ²值应该增加,粗略地说,得到一个非常大的χ²值的概率应该越来越小。

其中E是预期的计数数量,O是观察到的计数数量,这会在所有类别上进行求和。我们希望找到这个χ²统计量在分布中的位置,但为了有一个合适的分布,我们必须告诉函数考虑多少自由度(df)来进行测试。一般来说,我们在计算自由度时,从数据的类别数减一开始,所以在这个例子中有三个类别(ExpAA、ExpAS和ExpSS)减一。然而,我们还必须从观测数据中估计一个参数p,以生成每个类别的预期值。这意味着我们又失去了一个自由度。因此,df = 3 - 2 = 1(通过从观察数据中估计参数,预期数值“拟合”观察数据更紧密,所以这是有代价的)
chi2 <- (ExpAA-AA)^2/ExpAA+(ExpAS-AS)^2/ExpAS+(ExpSS-SS)^2/ExpSS
pvalue <- pchisq(chi2, df = 1, lower.tail = FALSE)
chi2
pvalue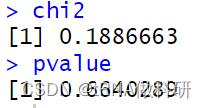
结果得到的P值(0.664>0.5),这表明我们的观察值与预期值相当一致(如果P值小于0.05,则认为一个值与预期显著不同)。因此,这个观察数据似乎完全符合我们从哈代-温伯格预测中所期望的结果。 χ²检验实际上是对似然比检验的一种便捷近似,这种检验被称为G检验或拟合优度检验,也常用于评估模型预测与实际现实世界数据之间的一致性:
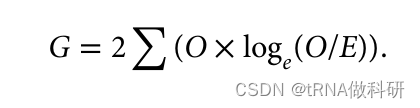
这种方法,顾名思义,关注的是我们的观察值与预期值的似然比。这种G检验方法使用与χ²检验相同的分布,并且表现相似。χ²检验通常被教授而不是G检验,因为它不需要你计算对数值;我们进行稍微更简化的G检验统计量的计算:
geno <- c(AA, AS, SS)
expe <- c(ExpAA, ExpAS, ExpSS)
G <- 2 * sum(geno * log(geno/expe))
pvalue <- pchisq(G, df = 1, lower.tail = FALSE)
G
pvalue

G检验得出的P值(0.668),与χ²检验(0.664)非常相似,因此我们再次相当确信我们的观察数据与我们的预期没有太大差异。
如果你还记得前一章的我们说哈代-温伯格预测的必要条件之一是没有任何遗传变异受到自然选择的影响。在这里,我们处理的等位基因对某一表型有重大影响,例如在纯合子时导致镰刀型贫血,在杂合子时赋予抗疟疾能力,这明显违反了这一假设(Luzzatto 2012)。但是,正如我们从刚才分析的血红蛋白S数据中看到的,这些假设经常被违反,然而与哈代-温伯格预期的偏离可能看起来非常小。我们看一个违法的例子:
哈代-温伯格假设之一是每一代配子的有效随机结合,无论潜在的等位基因频率如何。这在克隆物种中严重破坏,其中一个亲本产生一个与自己基因相同的后代。水蚤就是这样一种物种,雌性通常通过孤雌生殖(未受精的卵发育成胚胎)繁殖,一些种群甚至必须进行孤雌生殖(Paland等人,2005)

让我们来看一个例子,采集的118只水蚤个体,关于磷酸葡萄糖异构酶(PGI)的两个等位基因,我们再次称之为“A”和“S”,以便我们可以重用之前的代码(Hebert和Crease 1983)。发现了100个AS杂合子和34个AA纯合子,而SS纯合子在样本中完全缺失。我们再次进行卡方检验:
AA <- 34
AS <- 100
SS <- 0
N <- AA + AS + SS
p <- (SS + (AS/2))/N
p
ExpAA <- N*(1-p)^2
ExpAS <- N*2*p*(1-p)
ExpSS <- N*p^2chi2 <- (ExpAA-AA)^2/ExpAA+(ExpAS-AS)^2/ExpAS+(ExpSS-SS)^2/ExpSS
pvalue <- pchisq(chi2, df = 1, lower.tail = FALSE)
chi2
pvalue我们得到新的p值:

我们可以看到,这与我们的预期有很大的偏差,P值为5.56×10⁻¹²,我们可以得出结论,PGI基因中的至少一个变体超出哈代-温伯格条件下预期的东西;也就是说,我们没有在每个新世代中随机结合配子。 我们可以使用R函数barplot()将这些数据可视化为条形图。
dat <- matrix(c(geno,expe), nrow = 2, byrow = T)
barplot(dat,beside=T,col=c("turquoise4", "sienna1"),names.arg=c("AA", "SA", "SS"))
legend(x="topright", legend=c("Observed","Expected"),pch=15, col=c("turquoise4","sienna1"))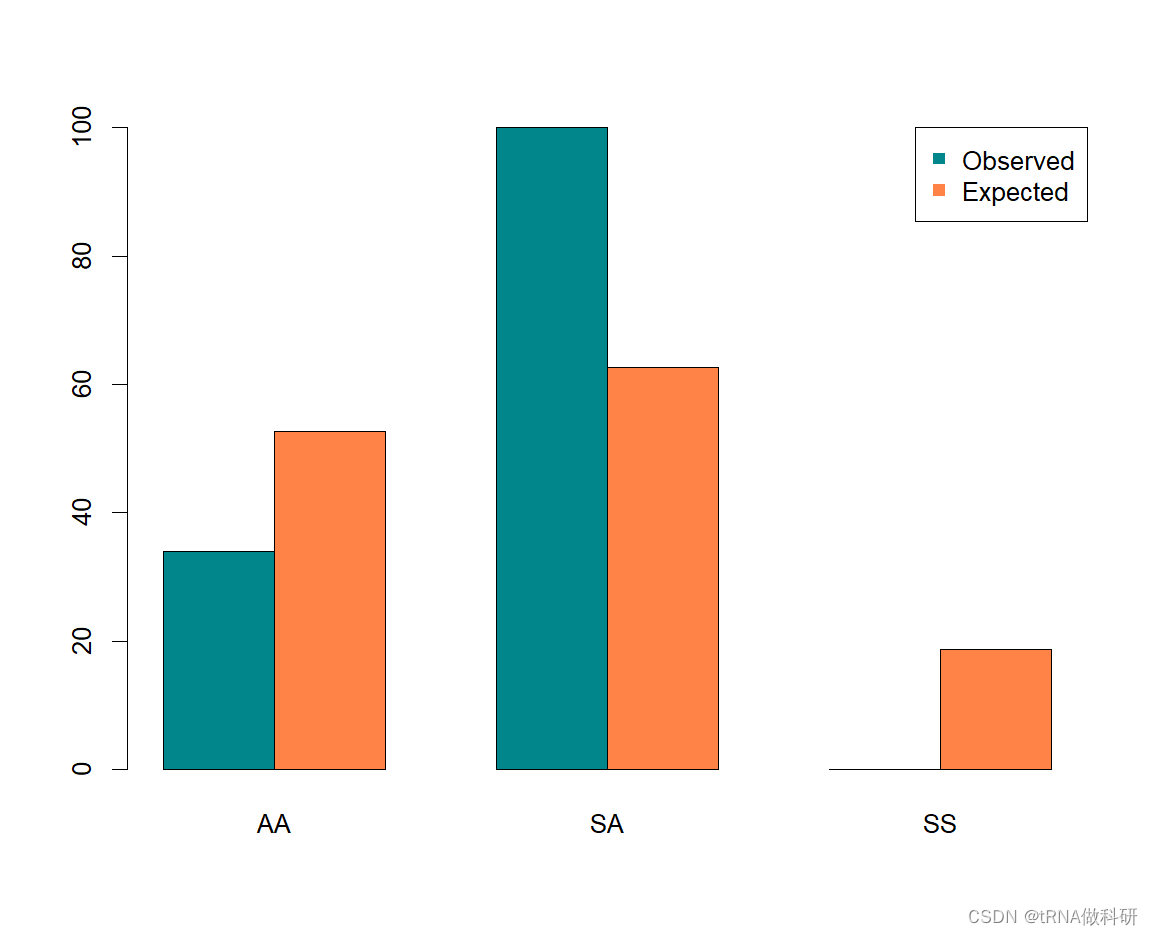
在处理较小的样本量时,考虑使用替代的检验方法可能更为合适,例如“精确检验”(exact test)。在精确检验中,会使用所有可能的等位基因基因型配置来为观察到的配置分配一个P值。关于这一背景下的精确检验的进一步讨论,可以参考Guo和Thompson(1992年)、Wigginton等人(2005年)、Engels(2009年)以及其中的参考文献。然而,一般来说,如果样本量足够大,能够检验感兴趣效应的大小,并且不过分关注接近显著性截断边界的结果(例如,Johnson 1999年),这些不同的统计方法在最终解释上将会是一致的。
原书内容写的有点不清晰,很多地方重复冗余,我进行提炼总结,许多R语言的错误我也进行了纠正,如果有什么问题,欢迎大家进行讨论。
下一篇博客我们将不只讨论两个等位基因的情况,而是进行一些拓展,下个博客见!
相关文章:

【基于R语言群体遗传学】-4-统计建模与算法(statistical tests and algorithm)
之前的三篇博客,我们对于哈代温伯格遗传比例有了一个全面的认识,没有看的朋友可以先看一下前面的博客: 群体遗传学_tRNA做科研的博客-CSDN博客 1.一些新名词 (1)Algorithm: A series of operations executed in a s…...

Java springboot校园管理系统源码
Java springboot校园管理系统源码-014 下载地址:https://download.csdn.net/download/xiaohua1992/89364089 技术栈 运行环境:jdk8 tomcat9 mysql5.7 windows10 服务端技术:Spring Boot Mybatis VUE 使用说明 1.使用Navicati或者其它工…...

Lianwei 安全周报|2024.07.01
新的一周又开始了,以下是本周「Lianwei周报」,我们总结推荐了本周的政策/标准/指南最新动态、热点资讯和安全事件,保证大家不错过本周的每一个重点! 政策/标准/指南最新动态 01 出于安全考虑,拜登下令禁用卡巴斯基杀毒…...

柯桥职场英语学习商务英语口语生活英语培训生活口语学习
辣妹用英语怎么说? 辣妹在英语中通常被翻译为“hot girl”或“spicy girl”,但更常见和直接的是“hot chick”或简单地使用“hot”来形容。 举个例子: Shes a real hot girl with her trendy outfit and confident attitude. 她真是个辣妹࿰…...

Spring与Quartz整合
Quartz框架是一个轻量级的任务调度框架,它提供了许多内置的功能,包括:支持作业的调度、集群调度、持久化、任务持久化、任务依赖、优先级、并发控制、失败重试等。同时也支持自定义作业类型和触发器类型。与Spring整合步骤如下: …...

C++之static关键字
文章目录 前提正文多重定义extern关键字使用staticstatic 全局变量(在.cpp文件中定义)static变量存放在哪里static变量可不可以放在.h文件中 static 函数static局部变量static 成员变量static 成员函数 总结参考链接 前提 好吧,八股,我又回来了。这次想…...
——day61)
嵌入式学习——硬件(Linux内核驱动编程platform、内核定时器、DS18B20)——day61
1. platform驱动框架 1.1 设备device #include <linux/init.h> #include <linux/module.h> #include <linux/platform_device.h>void led_release(struct device *dev) {printk("leds has been released\n"); }static struct resource led_resou…...

js逆向抠js要点解析与案例分享
JavaScript(JS)逆向工程是一种技术,用于分析和理解JS代码的功能和行为,尤其是在源代码不可用或被混淆的情况下。逆向JS代码可以帮助开发者理解第三方库的工作机制,或者在调试和优化过程中定位问题。 要点一࿱…...

mac安装docker
1、首先打开docker官网 https://docs.docker.com/engine/install/ 2、下载好后安装到app应用 3、安装好环境变量 #docker echo export PATH"/usr/local/Cellar/docker/20.10.11/bin:$PATH" >> .bash_profile...
PDF压缩工具选哪个?6款免费PDF压缩工具分享
PDF文件已经成为一种常见的文档格式。然而,PDF文件的体积有时可能非常庞大,尤其是在包含大量图像或复杂格式的情况下。选择一个高效的PDF压缩工具就显得尤为重要。小编今天给大家整理了2024年6款市面上反响不错的PDF压缩文件工具。轻松帮助你找到最适合自…...
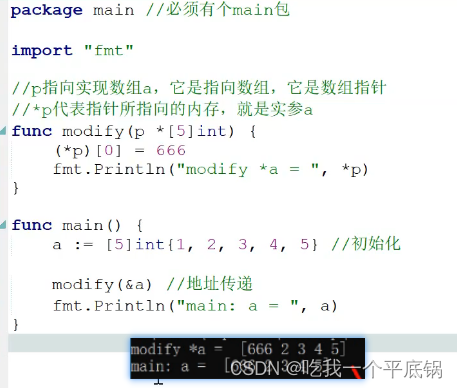
Go语言--复合类型之指针与数组
分类 指针 指针是一个代表着某个内存地址的值。这个内存地址往往是在内存中存储的另一个变量的值的起始位置。Go 语言对指针的支持介于 Java 语言和 C/C语言之间,它既没有想 Java 语言那样取消了代码对指针的直接操作的能力,也避免了 C/C语言中由于对指针的滥用而造成的安全和…...

docker 环境下failed to start lsb故障解决
背景:从深信服超融合迁移虚拟机到VMWARE集群后,迁移后的虚拟机 centos 7 运行systemctl start network ,报错 Restarting network (via systemctl): Job for network.service failed. See systemctl status network.service and journalctl -xn for d…...

Vue3学习(二)
回顾 DOM原生事件event对象 当事件发生时,浏览器会创建一个event对象,并将其作为参数传递给事件处理函数。这个对象包含了事件的详细信息,比如: type:事件的类型(如 click)target:…...

【C++】开源:地图投影和坐标转换proj库配置使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍地图投影和坐标转换proj库配置使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下&a…...
WordPress主题大前端DUX v8.7源码下载
全新:用户注册流程,验证邮箱,设置密码 新增:列表显示小视频和横幅视频 新增:文章内容中的外链全部增加 nofollow 新增:客服功能中的链接添加 nofollow 优化:产品分类的价格显示...

【论文阅读】自动驾驶光流任务 DeFlow: Decoder of Scene Flow Network in Autonomous Driving
再一次轮到讲自己的paper!耶,宣传一下自己的工作,顺便完成中文博客的解读 方便大家讨论。 Title Picture Reference and pictures paper: https://arxiv.org/abs/2401.16122 code: https://github.com/KTH-RPL/DeFlow b站视频: https://www.b…...

调和均值
文章目录 调和均值的定义和公式调和均值的几何解释调和均值的应用调和均值与算术平均和几何平均的比较示例 调和均值的定义和公式 调和均值是一种特殊的平均数,适用于处理涉及比率或速度的数据。对于一组正数 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2…...

DP学习——模板模式
学而时习之,温故而知新。 字面理解 模板?啥叫模板?模板就是固定死了,就是一套流程/步骤上层写死了。固定死了的流程或者步骤就是模板。然后我们要重写或者改写的是写死的这套流程中的节点。俗称“套模板”。 使用场合ÿ…...

AOP在业务中的简单使用
背景 业务组有一些给开发用的后门接口,为了做到调用溯源,业务组最近需要记录所有接口的访问记录,暂时只需要记录接口的响应结果,如果调用失败,则记录异常信息。由于后门接口较多以及只是业务组内部轻度使用࿰…...

C# 用户权限界面的测试内容
测试用户权限界面的主要目标是确保权限管理功能按照设计工作,同时保证用户界面响应正确,不会出现意外的行为或安全漏洞。以下是C#中用户权限界面测试的一些关键内容: 1. 功能性测试 权限分配与撤销:测试权限的分配和撤销功能&am…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
