AcWing 1550:完全二叉搜索树
【题目来源】
https://www.acwing.com/problem/content/1552/
【题目描述】
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
(1)若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
(2)若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
(3)它的左、右子树也分别为二叉搜索树
完全二叉树 (CBT) 定义为除最深层外的其他层的结点数都达到最大个数,最深层的所有结点都连续集中在最左边的二叉树。
现在,给定 N 个不同非负整数,表示 N 个结点的权值,用这 N 个结点可以构成唯一的完全二叉搜索树。
请你输出该完全二叉搜索树的层序遍历。
【输入格式】
第一行包含整数 N,表示结点个数。
第二行包含 N 个不同非负整数,表示每个结点的权值。
【输出格式】
共一行,输出给定完全二叉搜索树的层序遍历序列。
【数据范围】
1≤N≤1000,
结点权值不超过 2000。
【输入样例】
10
1 2 3 4 5 6 7 8 9 0
【输出样例】
6 3 8 1 5 7 9 0 2 4
【算法分析】
● 二叉搜索树(BST,Binary Search Tree)
二叉搜索树的形态与给定的序列值及顺序相关。也就是说,即便序列的值相同,但依据“左小右大”的原则,不同的次序也会生成不同形态的二叉搜索树。


(45,24,53,12,37,93) (12,24,37,45,53,93)
● 完全二叉树
如果在一棵具有n个结点的二叉树中,它的逻辑结构与满二叉树的前n个结点的逻辑结构相同,则称这样的二叉树为完全二叉树。显然,在完全二叉树中,结点 u 的左孩子为 2*u,右孩子为 2*u+1。

● 二叉搜索树具有一个重要的性质,即它的中序遍历序列是递增的。那又如何据此性质,输出二叉搜索树的层序遍历序列呢?
对二叉搜索树的结点值进行递增排序,然后执行类似于中序遍历的 dfs 操作,并在 dfs 过程中将对应的二叉搜索树结点值存入一个中序数组中,之后输出中序数组便可得到所求的二叉搜索树的层序遍历序列。
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=1010;
int a[maxn],in[maxn];
int n,idx;void dfs(int u) { //inorderif(u*2<=n) dfs(u*2);in[u]=a[idx++];if(u*2+1<=n) dfs(u*2+1);
}int main() {cin>>n;for(int i=0; i<n; i++) cin>>a[i];sort(a,a+n);dfs(1); //is 1,not 0. Otherwise,dfs can't run.for(int i=1; i<=n; i++) cout<<in[i]<<" ";return 0;
}/*
in:
10
1 2 3 4 5 6 7 8 9 0out:
6 3 8 1 5 7 9 0 2 4
*/
【参考文献】
https://blog.csdn.net/justinzengTM/article/details/81459482
https://www.acwing.com/solution/content/11649/
https://www.acwing.com/solution/content/97469/
相关文章:

AcWing 1550:完全二叉搜索树
【题目来源】https://www.acwing.com/problem/content/1552/【题目描述】二叉搜索树 (BST) 递归定义为具有以下属性的二叉树: (1)若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值 (2)若它的右…...

使用kali Linux启动盘轻松破解Windows电脑密码
破解分析文章仅限用于学习和研究目的;不得将上述内容用于商业或者非法用途,否则,一切后果请用户自负。谢谢!! 效果展示: 使用kali Linux可以轻松破解Windows用户及密码 准备阶段: (…...

Vue2中跨组件共享公共属性的方法、优缺点与实现
一、vuex(最常用) 优缺点 优点:集中管理状态,组件间解耦,易于调试和测试。缺点:学习成本较高,对于小项目可能过于复杂。 适用场景 大型、复杂的单页面应用(SPA)。需要全局…...
2024亚太杯数学建模竞赛(B题)的全面解析
你是否在寻找数学建模比赛的突破点?数学建模进阶思路! 作为经验丰富的数学建模团队,我们将为你带来2024亚太杯数学建模竞赛(B题)的全面解析。这个解决方案包不仅包括完整的代码实现,还有详尽的建模过程和解…...
【PWN · ret2syscall | GoPwn】[2024CISCN · 华中赛区]go_note
一道GoPwn,此外便是ret2syscall的利用。然而过程有不小的曲折,参考 返璞归真 师傅的wp,堪堪完成了复现。复现过程中,师傅也灰常热情回答我菜菜的疑问,感谢!2024全国大学生信息安全竞赛(ciscn&am…...

关于学习方法的优化
这是一种新的学习方法,一种新的学习形式,可以通过歌唱的方式,运用,把自己每天要进行的内容进行一个复习,进行一个重复,这样可以实现随时随地进行一个学习,这样可以帮助快速走出来! 您…...

万界星空科技MES系统中的排版排产功能
在当今高度竞争的市场环境中,企业对于生产管理的效率和质量要求日益提高。作为智能制造的重要组成部分,制造执行系统(MES)以其强大的功能,在提升企业生产能力方面发挥着不可替代的作用。万界星空科技作为行业领先的智能…...

kubeadm离线部署kubernetesv1.30.0
背景:最近由于docker image获取镜像受限的问题,以及公司内部部署kubernetes受限于内部网络无法访问公网的问题,对于离线部署kubernetes成为不是十分方便。谨以此文仅供参考。 kubernetes部署节点信息 kubernetes版本 1.30.0 操作系统版本&a…...

【PYG】dataloader和densedataloader
DenseDataLoader 是专门用于处理稠密图数据的,而 DataLoader 通常用于处理稀疏图数据。两者的主要区别在于它们的输入数据格式和处理方式。DenseDataLoader 适合处理固定大小的邻接矩阵和节点特征矩阵的数据,而 DataLoader 更加灵活,可以处理…...
: Access denied for user ‘root‘@‘localhost‘ (using password: NO))
完美解决ERROR 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using password: NO)
已解决ERROR 1045 (28000): Access denied for user ‘root‘‘localhost‘ (using password: NO) 下滑查看解决方法 文章目录 报错问题解决思路解决方法交流 报错问题 ERROR 1045 (28000): Access denied for user ‘root‘‘localhost‘ (using password: NO) 解决思路 对…...

ForkJoinPool 简介
引言 在现代并行编程中,处理大规模任务时将任务分割成更小的子任务并行执行是一种常见的策略。Java 提供了 Fork/Join 框架来支持这一模式,其中 ForkJoinPool 是其核心组件。本文将详细介绍 ForkJoinPool 的概念、使用方法和实际应用。 1. ForkJoinPoo…...

复现YOLO_ORB_SLAM3_with_pointcloud_map项目记录
文章目录 1.环境问题2.遇到的问题2.1编译问题1 monotonic_clock2.2 associate.py2.3 associate.py问题 3.运行问题 1.环境问题 首先环境大家就按照github上的指定环境安装即可 环境怎么安装网上大把的资源,自己去找。 2.遇到的问题 2.1编译问题1 monotonic_cloc…...

Docker:Docker网络
Docker Network 是 Docker 平台中的一项功能,允许容器相互通信以及与外界通信。它提供了一种在 Docker 环境中创建和管理虚拟网络的方法。Docker 网络使容器能够连接到一个或多个网络,从而使它们能够安全地共享信息和资源。 预备知识 推荐先看视频先有…...
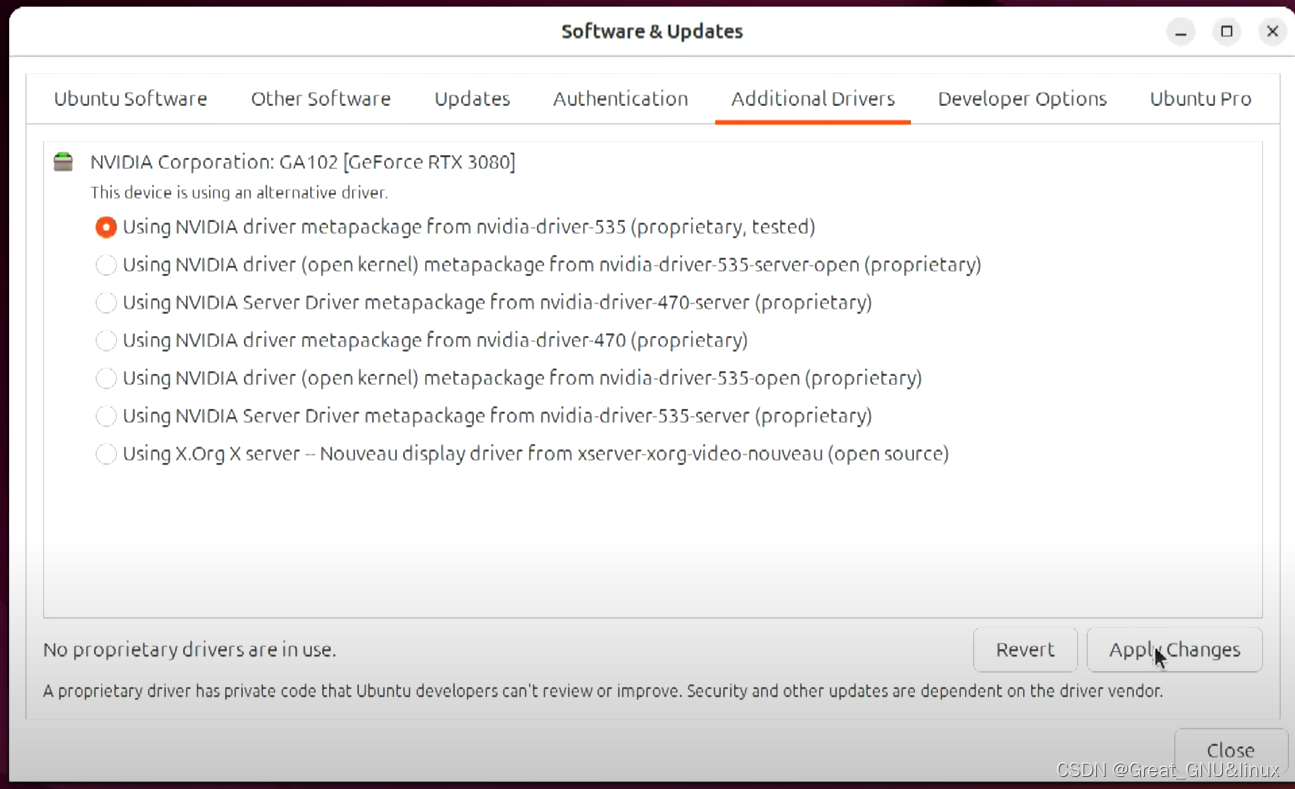
Ubuntu 24.04-自动安装-Nvidia驱动
教程 但在安全启动模式下可能会报错。 先在Nvidia官网找到GPU对应的驱动版, 1. 在软件与更新中选择合适的驱动 2. ubuntu自动安装驱动 sudo ubuntu-drivers autoinstall显示驱动 ubuntu-drivers devices3. 安装你想要的驱动 sudo apt install nvidia-driver-ve…...

【CSAPP】-attacklab实验
目录 实验目的与要求 实验原理与内容 实验设备与软件环境 实验过程与结果(可贴图) 实验总结 实验目的与要求 1. 强化机器级表示、汇编语言、调试器和逆向工程等方面基础知识,并结合栈帧工作原理实现简单的栈溢出攻击,掌握其基…...

docker部署onlyoffice,开启JWT权限校验Token
原来的部署方式 之前的方式是禁用了JWT: docker run -itd -p 8080:80 --name docserver --network host -e JWT_ENABLEDfalse --restartalways onlyoffice/documentserver:8 新的部署方式 参考文档:https://helpcenter.onlyoffice.com/installation/…...

Hive排序字段解析
Hive排序字段解析 在Hive中,CLUSTER BY、DISTRIBUTE BY、SORT BY和ORDER BY是用于数据分发和排序的关键子句,它们各自有不同的用途和性能特点。让我们逐一解析这些子句: 1. DISTRIBUTE BY 用途: 主要用于控制如何将数据分发到Reducer。它可…...

3101.力扣每日一题7/6 Java(接近100%解法)
博客主页:音符犹如代码系列专栏:算法练习关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 目录 思路 解题方法 时间复杂度 空间复杂度 Code 思路 主要是基于对…...

virtualbox窗口和win10窗口的切换
1、问题: 从windows切换到虚拟机可以用快捷键 ALTTAB,但是从虚拟机到windows使用 ALTTAB 无法成功切换 2、解决方法: 按下图操作 按上面步骤设置之后,每次要从虚拟机窗口切换到windows窗口 只需要先按 CtrlAlt 跳出虚拟机窗口&…...

卫星轨道平面简单认识
目录 一、轨道平面 1.1 轨道根数 1.2 应用考虑 二、分类 2.1 根据运行高度 2.2 根据运行轨迹偏心率 2.3 根据倾角大小 三、卫星星座中的轨道平面 四、设计轨道平面的考虑因素 一、轨道平面 1.1 轨道根数 轨道平面是定义卫星或其他天体绕行另一天体运动的平面。这个平…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
