注意力机制 attention Transformer 笔记
动手学深度学习
这里写自定义目录标题
- 注意力
- 加性注意力
- 缩放点积注意力
- 多头注意力
- 自注意力
- Transformer
注意力

注意力汇聚的输出为值的加权和
查询的长度为q,键的长度为k,值的长度为v。
q ∈ 1 × q , k ∈ 1 × k , v ∈ R 1 × v {\bf{q}} \in {^{1 \times q}},{{\bf{k}}} \in {^{1 \times k}},{{\bf{v}}} \in {\mathbb{R}^{1 \times v}} q∈1×q,k∈1×k,v∈R1×v
n个查询和m个键-值对
Q ∈ n × q , K ∈ m × k , V ∈ R m × v {\bf{Q}} \in {^{n \times q}},{\bf{K}} \in {^{m \times k}},{\bf{V}} \in {\mathbb{R}^{m \times v}} Q∈n×q,K∈m×k,V∈Rm×v
a ( Q , K ) ∈ R n × m {\bf{a}}\left( {{\bf{Q}},{\bf{K}}} \right) \in {\mathbb{R}^{n \times m}} a(Q,K)∈Rn×m是注意力评分函数
α ( Q , K ) = s o f t m a x ( a ( Q , K ) ) = exp ( a ( Q , K ) ) ∑ j = 1 m exp ( a ( Q , K ) ) ∈ R n × m {\boldsymbol{\alpha}} \left( {{\bf{Q}},{\bf{K}}} \right) = {\rm{softmax}}\left( {{\bf{a}}\left( {{\bf{Q}},{\bf{K}}} \right)} \right) = \frac{{\exp \left( {{\bf{a}}\left( {{\bf{Q}},{\bf{K}}} \right)} \right)}}{{\sum\limits_{j = 1}^m {\exp \left( {{\bf{a}}\left( {{\bf{Q}},{\bf{K}}} \right)} \right)} }} \in {\mathbb{R}^{n \times m}} α(Q,K)=softmax(a(Q,K))=j=1∑mexp(a(Q,K))exp(a(Q,K))∈Rn×m是注意力权重
f ( Q , K , V ) = α ( Q , K ) ⊤ V ∈ R n × v f({\bf{Q}},{\bf{K}},{\bf{V}}) = {\boldsymbol{\alpha}} {\left( {{\bf{Q}},{\bf{K}}} \right)^ \top }{\bf{V}} \in {\mathbb{R}^{n \times v}} f(Q,K,V)=α(Q,K)⊤V∈Rn×v是注意力汇聚函数
加性注意力
q ∈ R 1 × q , k ∈ R 1 × k {\bf{q}} \in {\mathbb {R}^{1 \times q}},{\bf{k}} \in {\mathbb {R}^{1 \times k}} q∈R1×q,k∈R1×k
W q ∈ R h × q , W k ∈ R h × k , w v ∈ R h × 1 {{\bf{W}}_q} \in {{\mathbb R}^{h \times q}},{{\bf{W}}_k} \in {{\mathbb R}^{h \times k}},{{\bf{w}}_v} \in {{\mathbb R}^{h \times 1}} Wq∈Rh×q,Wk∈Rh×k,wv∈Rh×1
a ( q , k ) = w v ⊤ t a n h ( W q q ⊤ + W k k ⊤ ) ∈ R a({\bf{q}},{\bf{k}}) = {\bf{w}}_v^ \top {\rm{tanh}}({{\bf{W}}_q}{{\bf{q}}^ \top } + {{\bf{W}}_k}{{\bf{k}}^ \top }) \in \mathbb {R} a(q,k)=wv⊤tanh(Wqq⊤+Wkk⊤)∈R是注意力评分函数
缩放点积注意力
q ∈ R 1 × d , k ∈ R 1 × d , v ∈ R 1 × v {\bf{q}} \in \mathbb{R}{^{1 \times d}},{\bf{k}} \in \mathbb{R}{^{1 \times d}},{\bf{v}} \in {{\mathbb R}^{1 \times v}} q∈R1×d,k∈R1×d,v∈R1×v
a ( q , k ) = 1 d q k ⊤ ∈ R a\left( {{\bf{q}},{\bf{k}}} \right) = \frac{1}{{\sqrt d }}{\bf{q}}{{\bf{k}}^ \top } \in \mathbb{R} a(q,k)=d1qk⊤∈R是注意力评分函数
f ( q , k , v ) = α ( q , k ) ⊤ v = s o f t m a x ( 1 d q k ⊤ ) v ∈ R 1 × v f({\bf{q}},{\bf{k}},{\bf{v}}) = \alpha {\left( {{\bf{q}},{\bf{k}}} \right)^ \top }{\bf{v}} = {\rm{softmax}}\left( {\frac{1}{{\sqrt d }}{\bf{q}}{{\bf{k}}^ \top }} \right){\bf{v}} \in {{\mathbb R}^{1 \times v}} f(q,k,v)=α(q,k)⊤v=softmax(d1qk⊤)v∈R1×v是注意力汇聚函数
n个查询和m个键-值对
Q ∈ R n × d , K ∈ R m × d , V ∈ R m × v \mathbf Q\in\mathbb R^{n\times d}, \mathbf K\in\mathbb R^{m\times d}, \mathbf V\in\mathbb R^{m\times v} Q∈Rn×d,K∈Rm×d,V∈Rm×v
a ( Q , K ) = 1 d Q K ⊤ ∈ R n × m {\bf{a}}\left( {{\bf{Q}},{\bf{K}}} \right) = \frac{1}{{\sqrt d }}{\bf{Q}}{{\bf{K}}^ \top } \in {\mathbb{R}^{n \times m}} a(Q,K)=d1QK⊤∈Rn×m是注意力评分函数
f ( Q , K , V ) = α ( Q , K ) ⊤ V = s o f t m a x ( 1 d Q K ⊤ ) V ∈ R n × v f({\bf{Q}},{\bf{K}},{\bf{V}}) = {\boldsymbol{\alpha}} {\left( {{\bf{Q}},{\bf{K}}} \right)^ \top }{\bf{V}} ={\rm{softmax}}\left( {\frac{1}{{\sqrt d }}{\bf{Q}}{{\bf{K}}^ \top }} \right){\bf{V}} \in {\mathbb{R}^{n \times v}} f(Q,K,V)=α(Q,K)⊤V=softmax(d1QK⊤)V∈Rn×v是注意力汇聚函数
多头注意力
q ∈ R 1 × d q , k ∈ R 1 × d k , v ∈ R 1 × d v {\bf{q}} \in {{\mathbb R}^{1 \times {d_q}}},{\bf{k}} \in {{\mathbb R}^{1 \times {d_k}}},{\bf{v}} \in {{\mathbb R}^{1 \times {d_v}}} q∈R1×dq,k∈R1×dk,v∈R1×dv
W i ( q ) ∈ R p q × d q , W i ( k ) ∈ R p k × d k , W i ( v ) ∈ R p v × d v {\bf{W}}_i^{(q)} \in {{\mathbb R}^{{p_q} \times {d_q}}},{\bf{W}}_i^{(k)} \in {{\mathbb R}^{{p_k} \times {d_k}}},{\bf{W}}_i^{(v)} \in {{\mathbb R}^{{p_v} \times {d_v}}} Wi(q)∈Rpq×dq,Wi(k)∈Rpk×dk,Wi(v)∈Rpv×dv
h i = f ( W i ( q ) q ⊤ , W i ( k ) k ⊤ , W i ( v ) v ⊤ ) ∈ R 1 × p v {{\bf{h}}_i} = f\left( {{\bf{W}}_i^{(q)}{{\bf{q}}^ \top },{\bf{W}}_i^{(k)}{{\bf{k}}^ \top },{\bf{W}}_i^{(v)}{{\bf{v}}^ \top }} \right) \in {{\mathbb R}^{{1 \times p_v}}} hi=f(Wi(q)q⊤,Wi(k)k⊤,Wi(v)v⊤)∈R1×pv是注意力头
W o ∈ R p o × h p v {{\bf{W}}_o} \in {{\mathbb R}^{{p_o} \times h{p_v}}} Wo∈Rpo×hpv
W o [ h 1 ⊤ ⋮ h h ⊤ ] ∈ R p o {{\bf{W}}_o}\left[ {\begin{array}{c} {{{\bf{h}}_1^ \top}}\\ \vdots \\ {{{\bf{h}}_h^ \top}} \end{array}} \right] \in {{\mathbb R}^{{p_o}}} Wo h1⊤⋮hh⊤ ∈Rpo
p q h = p k h = p v h = p o p_q h = p_k h = p_v h = p_o pqh=pkh=pvh=po

多头注意力:多个注意力头连结然后线性变换
自注意力
x i ∈ R 1 × d , X = [ x 1 ⋯ x n ] ∈ R n × d {{\bf{x}}_i} \in {{\mathbb R}^{1 \times d}},{\bf{X}} = \left[ {\begin{array}{c} {{{\bf{x}}_1}}\\ \cdots \\ {{{\bf{x}}_n}} \end{array}} \right] \in {{\mathbb R}^{n \times d}} xi∈R1×d,X= x1⋯xn ∈Rn×d
Q = X , K = X , V = X {\bf{Q}} = {\bf{X}},{\bf{K}} = {\bf{X}},{\bf{V}} = {\bf{X}} Q=X,K=X,V=X
f ( Q , K , V ) = α ( Q , K ) ⊤ V = s o f t m a x ( 1 d Q K ⊤ ) V ∈ R n × d f({\bf{Q}},{\bf{K}},{\bf{V}}) = {\boldsymbol{\alpha}} {\left( {{\bf{Q}},{\bf{K}}} \right)^ \top }{\bf{V}} ={\rm{softmax}}\left( {\frac{1}{{\sqrt d }}{\bf{Q}}{{\bf{K}}^ \top }} \right){\bf{V}} \in {\mathbb{R}^{n \times d}} f(Q,K,V)=α(Q,K)⊤V=softmax(d1QK⊤)V∈Rn×d
y i = f ( x i , ( x 1 , x 1 ) , … , ( x n , x n ) ) ∈ R d {{\bf{y}}_i} = f\left( {{{\bf{x}}_i},\left( {{{\bf{x}}_1},{{\bf{x}}_1}} \right), \ldots ,\left( {{{\bf{x}}_n},{{\bf{x}}_n}} \right)} \right) \in {{\mathbb R}^d} yi=f(xi,(x1,x1),…,(xn,xn))∈Rd
n个查询和m个键-值对
Q = t a n h ( W q X ) ∈ R n × d {\bf{Q}} = {\rm{tanh}}\left( {{{\bf{W}}_q}{\bf{X}}} \right) \in {{\mathbb R}^{n \times d}} Q=tanh(WqX)∈Rn×d
K = t a n h ( W k X ) ∈ R m × d {\bf{K}} = {\rm{tanh}}\left( {{{\bf{W}}_k}{\bf{X}}} \right) \in {{\mathbb R}^{m \times d}} K=tanh(WkX)∈Rm×d
V = t a n h ( W v X ) ∈ R m × v {\bf{V}} = {\rm{tanh}}\left( {{{\bf{W}}_v}{\bf{X}}} \right) \in {{\mathbb R}^{m \times v}} V=tanh(WvX)∈Rm×v
J. Xu, F. Zhong, and Y. Wang, “Learning multi-agent coordination for enhancing target coverage in directional sensor networks,” in Proc. Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, Dec. 2020, pp. 1–16.
https://github.com/XuJing1022/HiT-MAC/blob/main/perception.py
x i ∈ R 1 × d i n , X = [ x 1 ⋯ x n m ] ∈ R n m × d i n {{\bf{x}}_i} \in {{\mathbb R}^{1 \times d_{in}}},{\bf{X}} = \left[ {\begin{array}{c} {{{\bf{x}}_1}}\\ \cdots \\ {{{\bf{x}}_{nm}}} \end{array}} \right] \in {{\mathbb R}^{nm \times d_{in}}} xi∈R1×din,X= x1⋯xnm ∈Rnm×din
W ∈ R d a t t × d i n {\bf{W}} \in {{\mathbb R}^{d_{att}\times d_{in}}} W∈Rdatt×din
Q = t a n h ( W q X ⊤ ) ⊤ ∈ R n m × d a t t {\bf{Q}} = {\rm{tanh}}\left( {{{\bf{W}}_q}{\bf{X}}^\top} \right)^\top \in {{\mathbb R}^{nm \times d_{att}}} Q=tanh(WqX⊤)⊤∈Rnm×datt
K = t a n h ( W k X ⊤ ) ⊤ ∈ R n m × d a t t {\bf{K}} = {\rm{tanh}}\left( {{{\bf{W}}_k}{\bf{X}}^\top} \right)^\top \in {{\mathbb R}^{nm \times d_{att}}} K=tanh(WkX⊤)⊤∈Rnm×datt
V = t a n h ( W v X ⊤ ) ⊤ ∈ R n m × d a t t {\bf{V}} = {\rm{tanh}}\left( {{{\bf{W}}_v}{\bf{X}}^\top} \right)^\top \in {{\mathbb R}^{nm \times d_{att}}} V=tanh(WvX⊤)⊤∈Rnm×datt
f ( Q , K , V ) = α ( Q , K ) ⊤ V = s o f t m a x ( 1 d Q K ⊤ ) V ∈ R n m × d a t t f({\bf{Q}},{\bf{K}},{\bf{V}}) = {\boldsymbol{\alpha}} {\left( {{\bf{Q}},{\bf{K}}} \right)^ \top }{\bf{V}} ={\rm{softmax}}\left( {\frac{1}{{\sqrt d }}{\bf{Q}}{{\bf{K}}^ \top }} \right){\bf{V}} \in {{\mathbb R}^{nm \times d_{att}}} f(Q,K,V)=α(Q,K)⊤V=softmax(d1QK⊤)V∈Rnm×datt
class AttentionLayer(torch.nn.Module):def __init__(self, feature_dim, weight_dim, device):super(AttentionLayer, self).__init__()self.in_dim = feature_dimself.device = deviceself.Q = xavier_init(nn.Linear(self.in_dim, weight_dim))self.K = xavier_init(nn.Linear(self.in_dim, weight_dim))self.V = xavier_init(nn.Linear(self.in_dim, weight_dim))self.feature_dim = weight_dimdef forward(self, x):# param x: [num_agent, num_target, in_dim]# return z: [num_agent, num_target, weight_dim]# z = softmax(Q,K)*Vq = torch.tanh(self.Q(x)) # [batch_size, sequence_len, weight_dim]k = torch.tanh(self.K(x)) # [batch_size, sequence_len, weight_dim]v = torch.tanh(self.V(x)) # [batch_size, sequence_len, weight_dim]z = torch.bmm(F.softmax(torch.bmm(q, k.permute(0, 2, 1)), dim=2), v) # [batch_size, sequence_len, weight_dim]global_feature = z.sum(dim=1)return z, global_feature
Transformer

相关文章:

注意力机制 attention Transformer 笔记
动手学深度学习 这里写自定义目录标题 注意力加性注意力缩放点积注意力多头注意力自注意力Transformer 注意力 注意力汇聚的输出为值的加权和 查询的长度为q,键的长度为k,值的长度为v。 q ∈ 1 q , k ∈ 1 k , v ∈ R 1 v {\bf{q}} \in {^{1 \times…...
开始尝试从0写一个项目--后端(二)
实现学生管理 新增学生 接口设计 请求路径:/admin/student 请求方法:POST 请求参数:请求头:Headers:"Content-Type": "application/json" 请求体:Body: id 学生id …...
【图解大数据技术】Hive、HBase
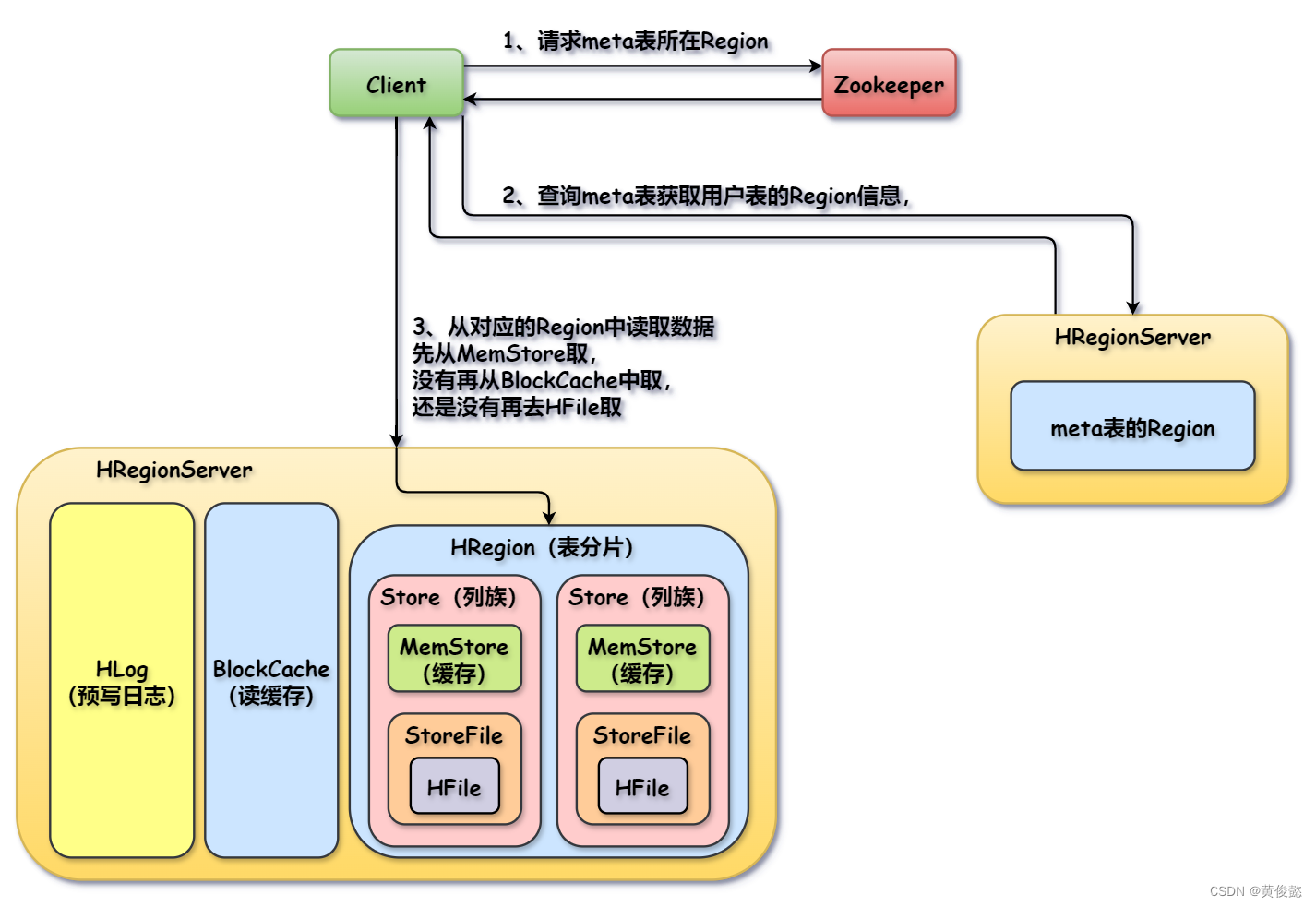
【图解大数据技术】Hive、HBase Hive数据仓库Hive的执行流程Hive架构数据导入Hive HBaseHBase简介HBase架构HBase的列式存储HBase建表流程HBase数据写入流程HBase数据读取流程 Hive Hive是基于Hadoop的一个数据仓库工具,Hive的数据存储在HDFS上,底层基于…...
)
composables 目录下的文件(web前端)
composables 目录通常用于存放可组合的函数或逻辑,这些函数或逻辑可以在不同的组件中复用。具体来说,composables 目录下的文件通常包含以下内容: 组合式函数 (Composable Functions): 这些函数利用 Vue 3 的组合式 API࿰…...

使用Python绘制堆积柱形图
使用Python绘制堆积柱形图 堆积柱形图效果代码 堆积柱形图 堆积柱形图(Stacked Bar Chart)是一种数据可视化图表,用于显示不同类别的数值在某一变量上的累积情况。每一个柱状条显示多个子类别的数值,子类别的数值在柱状条上堆积在…...

DP:二维费用背包问题
文章目录 🎵二维费用背包问题🎶引言🎶问题定义🎶动态规划思想🎶状态定义和状态转移方程🎶初始条件和边界情况 🎵例题🎶1.一和零🎶2.盈利计划 🎵总结 …...

C语言标准库中的函数
由于C语言标准库中的函数非常多,我将按类别列出一些常见函数及其作用。请注意,这里不可能列出所有函数,但我会尽量覆盖主要的类别和函数。 ### 标准输入输出 - printf: 格式化输出到标准输出(通常是屏幕)。 - scanf: …...

Qt5.9.9 关于界面拖动导致QModbusRTU(QModbusTCP没有测试过)离线的问题
问题锁定 参考网友的思路: Qt5.9 Modbus request timeout 0x5异常解决 网友认为是Qt的bug, 我也认同;网友认为可以更新模块, 我也认同, 我也编译了Qt5.15.0的code并成功安装到Qt5.9.9中进行使用,界面拖…...

API的定义理解
前言 在程序员的日常工作中,“API”这个词在程序员的口中重复的次数,绝对是名列前茅的。 但是对刚开始工作的新人来说,API这个概念还是比较模糊。 确实,API这个概念是随着语义环境而不一样的,所以会让人迷惑。 下面…...

启航IT之旅:高考假期预习指南
标题:启航IT之旅:高考假期预习指南 随着高考的落幕,许多有志于IT领域的学子们即将踏上新的学习旅程。这个假期,是他们探索IT世界的黄金时期。本文将为准IT新生们提供一份全面的预习指南,帮助他们为未来的学习和职业生…...

HarmonyOS开发:循环渲染ForEach
需求: 创建多个列表组件,并实现点赞功能 语言: ArkTS 平台: DevEco Studio ForEach 接口描述 ForEach( arr: Array, itemGenerator: (item: Object, index: number) > void, keyGenerator?: (item: Object, index: number) &…...

构建工程化:多种不同的工程体系如何编写MakeFile
源码分析 核心MakeFile 这个 Makefile 是一个复杂的构建脚本,用于管理和构建一个大型项目。它包括多个目标、条件判断和递归调用 make 命令来处理多个子项目和子目录。让我们逐部分进行详细解析。 伪目标和变量定义 .PHONY: all clean install build test init.…...

聚焦从业人员疏散逃生避险意识能力提升,推动生产经营单位每年至少组织开展(疏散逃生演练,让全体从业人员熟知逃生通道、安全出口及应急处置要求,形成常态化机制。
聚焦从业人员疏散逃生避险意识能力提升,推动生产经营单位每年至少组织开展(疏散逃生演练,让全体从业人员熟知逃生通道、安全出口及应急处置要求,形成常态化机制。完整试题答案查看 A.三次B.两次C.一次 综合运用“四不两直”、明察暗访、 ()、…...
【手机取证】如何使用360加固助手给apk加固
文章关键词:手机取证、电子数据取证、数据恢复 一、前言 APP加固是对APP代码逻辑的一种保护。原理是将应用文件进行某种形式的转换,包括不限于隐藏,混淆,加密等操作,进一步保护软件的利益不受损坏,下面给…...

Vue的介绍
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

MySql数据库常用指令合集
MySql数据库常用指令合集 一、创建数据库db11.创建表 字段---表头 student_no,username,sex2.新增单条插入多条插入3.删除4.更新5.查询5.1.查询该表全部信息5.2.查询该表中username,并且要求名字为zhangsan性别女,还可以用(or) 6.…...
编辑 13 注解)
ArcGIS Pro SDK (七)编辑 13 注解
ArcGIS Pro SDK (七)编辑 13 注解 文章目录 ArcGIS Pro SDK (七)编辑 13 注解1 注释构建工具2 以编程方式启动编辑批注3 更新批注文本4 修改批注形状5 修改批注文本图形6 接地到网格 环境:Visual Studio 2022 .NET6 …...

模拟面试001-Java开发工程师+简历+问题+回答
模拟面试001-Java开发工程师简历问题回答 目录 模拟面试001-Java开发工程师简历问题回答面试简历面试官题问求职者回答1. 关于Java编程和技术栈2. 关于XX在线购物平台项目3. 关于XX企业资源规划系统项目4. 团队协作与项目管理5. 个人发展与职业规划 参考资料 面试简历 **个人信…...

微信小程序 ——入门介绍及简单的小程序编写
目录 一、小程序入门 1.1 什么是小程序 1.2 小程序的优点 1.3 小程序注册 1.4 安装开发工具 1.5 创建第一个小程序 二、小程序目录结构及入门案例 2.1 目录结构 2.2 入门案例 2.2.1 创建界面 2.2.2 设置标题 2.2.3 编写WXML文件 2.2.4 编写JS文件 2.2.5 编写WXSS…...

ubuntu20.04安装lio-sam
1、依赖功能包安装 sudo apt install ros-noetic-robot-state-publisher sudo apt-get install ros-noetic-robot-localization libmetis-dev 2、boost版本 boost版本查看:cat /usr/include/boost/version.hpp | grep "BOOST_LIB_VERSION" boost版本为1.…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
