归并排序有多简单?一幅图教你看懂【C语言】

目录
归并排序的递归实现
代码实现
归并排序的非递归实现
代码实现
归并排序的思想很简单——分治法。简单地说,归并排序的是将序列拆分成几段子序列,将每一段子序列分别进行排序,排好之后再将有序的子序列归并(有点像合并两个有序数组)成为一个有序的序列。
例如要排序数列:10、6、7、1、3、9、4、2;

将序列拆分为 2 个子序列;
继续拆分;

继续拆分;

至此,每个子序列的长度都为 1 ,因为只有一个数,所以可认为是有序序列;
现将子序列两两归并,即合并两个有序序列;

继续归并;
 继续归并;
继续归并;
 以上就是归并排序的整个过程,很显然归并排序的实现应该离不开递归的思想。
以上就是归并排序的整个过程,很显然归并排序的实现应该离不开递归的思想。

归并排序的递归实现
归并排序的递归实现较为简单,需要注意的有两点:
1. 归并的过程并非在原数组上直接改动,而是开辟一个临时数组,在临时数组上进行排序,排好之后将临时数组的内容全部拷贝到原数组;
2. 代码中使用的是二路归并(如上图所示,每次将序列拆分为两个子序列)。
代码实现
void _MergeSort(int* a, int begin, int end, int* tmp)
{//递归的结束条件//当序列只有一个元素时或序列不存在时if (begin >= end)return;//将序列进行拆分 //[begin,mid] [mid+1,end]int mid = (begin + end) / 2;//拆分的过程_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);//以下为归并的过程int begin1 = begin, end1 = mid;int begin2 = mid+1, end2 = end;int i = begin;//归并:合并两个有序序列while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}//如果第二段序列先结束while (begin1 <= end1){tmp[i++] = a[begin1++];}//如果第一段序列先结束while (begin2 <= end2){tmp[i++] = a[begin2++];}//将临时数组的数据拷贝回原数组memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a,int n)
{//开辟一个临时数组int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}_MergeSort(a, 0, n - 1, tmp);//释放与置空free(tmp);tmp = NULL;
}归并排序的非递归实现
非递归与递归作用思想基本相同。递归实现时,因为拆分序列时采用的是递归的方式,所以通过传递参数就可以控制子序列的长度。但是非递归不行,非递归通过变量 rangeN 来控制序列的长度(或间隔),每次让 rangeN *= 2 例如:

但是由于 rangeN 每次都 *2 ,而我们排序的序列长度不可能总是 2 的倍数,所以 可能会有数组越界访问的风险。例如:

现将两个子序列归并,并将数据拷贝回原数组时,就会发生越界:
 当然这只是其中一种越界的可能情况——第二段序列发生越界,原因是右边界 end2 大于 n;
当然这只是其中一种越界的可能情况——第二段序列发生越界,原因是右边界 end2 大于 n;
实际操作中,一共会有三种情况导致越界:
两段序列的区间分别为: [begin1,end1] [begin2,end2]
1. end1 > n;
2. begin > n;
3.end2 > n;
所以,当这三种情况发生时,需要修正区间,以上述用例为例, end2 大于 n 时,令 end2 = n-1即可;
代码实现
void MergeSortNonR(int* a, int n)
{//开辟一个临时数组int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}int rangeN = 1;while (rangeN < n){// i 控制访问子序列的位置for (int i = 0; i < n; i += 2 * rangeN){//拆分为两段子序列//[begin1,end1] [begin2,end2]int begin1 = i, end1 = i + rangeN - 1;int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;int j = i;//判断是否发生越界的三种情况,如果有,就修正区间if (end1 >= n){end1 = n - 1;//将第二段序列改为不存在的序列即可begin2 = n;end2 = n - 1;}else if (begin2 >= n){//将第二段序列改为不存在的序列即可begin2 = n;end2 = n - 1;}else if (end2 >= n){//修正区间end2 = n-1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//如果第二段序列先结束while (begin1 <= end1){tmp[j++] = a[begin1++];}//如果第一段序列先结束while (begin2 <= end2){tmp[j++] = a[begin2++];}}//将临时数组的内容拷贝回原数组memcpy(a, tmp, sizeof(int) * n);//控制间隔rangeN *= 2;}//释放与置空free(tmp);tmp = NULL;
}相关文章:

归并排序有多简单?一幅图教你看懂【C语言】
目录 归并排序的递归实现 代码实现 归并排序的非递归实现 代码实现 归并排序的思想很简单——分治法。简单地说,归并排序的是将序列拆分成几段子序列,将每一段子序列分别进行排序,排好之后再将有序的子序列归并(有点像合并两…...
)
C++-Z字扫描实现(Zigzag Scan)
Z字扫描(Zigzag Scan) 将二维矩阵压缩成行输出: int index0; for(int i0;i<rowscols-1;i){//i是第几条对角线if(i&1){//odd,向下扫描for(int jmax(0,i-cols1);j<min(i,row-1);j){res[index]mtx[j][i-j];}//}else{//偶数,向上扫描for(int jmi…...

【华为机试真题详解 Python实现】求最大数字【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1示例 2题目解析参考代码前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即…...
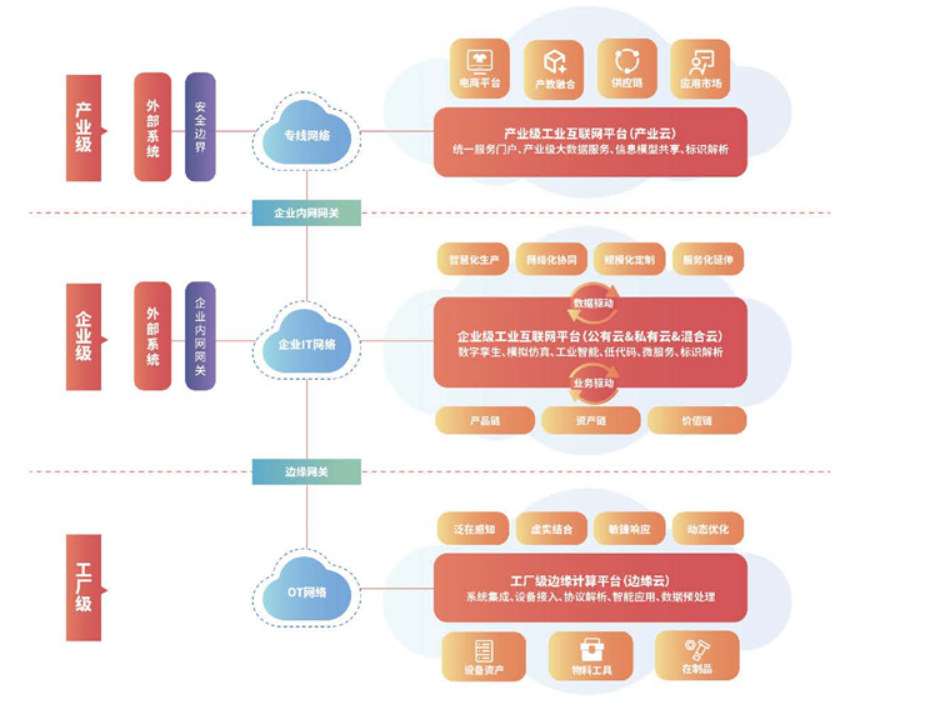
面对数万亿产业规模,如何掘金工业互联网?
近年来,加速工业互联网建设的声音越来越响亮。一方面,政策利好,持续驱动。从2017年的《国务院关于深化“互联网先进制造业” 发展工业互联网的指导意见》到《工业互联网创新发展三年行动计划(2021-2023年)》࿰…...
)
#ifdefine #define #endif (避免头文件被重复包含的真正含义)
宏定义 首先在谈论正式话题之前,需要先介绍一个基础概念,也是前提,那就是宏定义。 #define demo 1 #define PI 3.14我们都知道这样会将demo 在预处理阶段替换或者说展开为1,Pi 替换为3.14。 #define 宏定义一个标识符来表示一个…...

单片机能运行操作系统吗?
先直接上答案:可以!但是操作系统不是刚需,上操作系统比较占用单片机的资源,比如占用比较多的FLASH和RAM,间接增加了硬件成本,哪怕成本增加1毛钱,对于上量的产品,分分钟是一个工程师的…...
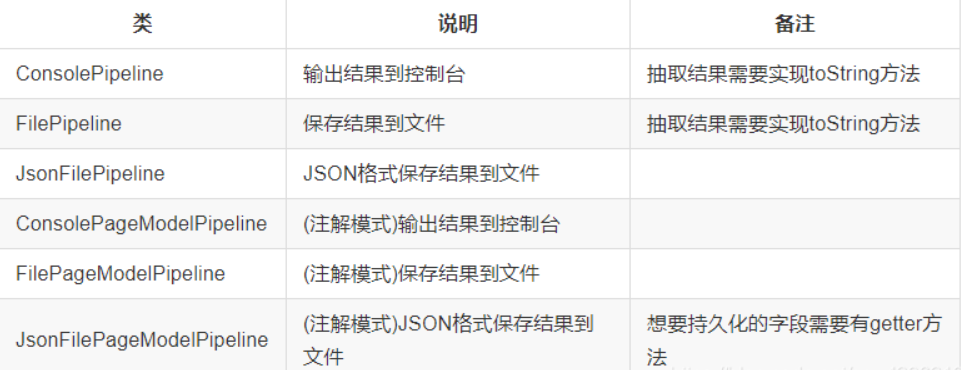
Python之webmagic爬虫优点与使用
一、webmagic的优点它更偏向于java的语法,对于熟悉java的工程师来说学习成本较低。提供多种选择器,如css选择器、xpath、正则等。有一个模块pipeline:可通过简单地配置,可以将爬虫抽取到的信息,持久化到文件、数据库等…...

代码随想录动态规划 || 121 122
Day42121. 买卖股票的最佳时机力扣题目链接给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返…...
C++STL库中不可或缺的部分—string(模拟实现)
前文大家好,本篇文章主要是讲解一下string一些常用接口的模拟实现。众所周知,在日常生活中,字符串无处不在,如just do it,中国,一坤年等,想要在计算机上将这些字符展现出来就需要用到string类,而对我们C程序…...

MySQL复合查询
文章目录基本查询回顾多表查询自连接子查询单行子查询多行子查询多列子查询在from子句中使用子查询合并查询unionunion all基本查询回顾 查询的员工部门表结构: mysql> show tables; ----------------- | Tables_in_scott | ----------------- | dept …...

PCIe 资料收集2
文章目录感官认识PCIe的存储空间PCIe 在 linux 下的驱动PCIe 验证1.PCIe 传递裸数据2.PCIe 转其他设备PCIe转其他总线RS232USB从用户空间理解PCIe感官认识 总线协议接口 视频介绍PCIe 视频介绍及PCIe文字介绍 PCIe上可以接各种控制器硬盘控制器硬盘声卡控制器音响咪头/耳机显…...
)
Linux网络编程(使用VScode远程登录ubuntu)
文章目录 前言一、SSH插件的安装1.SSH简单介绍2.SSH插件安装和配置步骤二、安装C/C++插件总结前言 本篇文章将带大家进行网络编程的准备工作,使用vscode进行远程登录ubuntu。为什么要使用vscode进行远程登录ubantu呢?因为有些小伙伴的电脑可能性能不够开启虚拟机后会导致电脑…...

如何提高项目估算精准度?关键看5大影响因子
如何让项目估算工作更加精准,我们需要重点关注5大调整因子。 1、功能点调整因子 首先需要对功能点因子进行调整,区分不同类型的系统特征值。 因为不同的系统,对项目开发的影响程度不同,一般我们把系统特征值分为14种类型ÿ…...

论文阅读笔记《Nctr: Neighborhood Consensus Transformer for Feature Matching》
核心思想 本文提出一种融合邻域一致性的Transfomer结构来实现特征点的匹配(NCTR)。整个的实现流程和思想与SuperGlue相似,改进点在于考虑到了邻域一致性。邻域一致性在许多的传统图像匹配和图匹配任务中都有应用,他基于一个很重要…...

上位机系统Ubuntu 20.04与下位机arduino UNO通讯
目录一、安装arduino IDE1.1安装方法1.1.1终端里命令下载(不推荐)1.1.2官网下载(不推荐)1.1.3论坛下载(不推荐)1.1.4系统应用商店(推荐!)1.2配置项目文件位置1.3测试IDE功…...

hive面试题
1、什么是Hive Hive是基于Hadoop的一个数据仓库工具,可以将结构化的数据文件映射为一张数据库表,并提供类SQL查询功能(HQL) 2、Hive的意义(最初研发的原因) 避免了去写MapReduce,提供快速开发的…...

【CUDA】《CUDA编程:基础与实践》CUDA加速的关键因素
CUDA事件计时 CUDA提供了一种基于CUDA事件(CUDA event)的计时方式,可用来给一段CUDA代码(可能包含主机代码和设备代码)计时。 对计时器的封装: class CUDATimeCost { public:void start() {elapsed_time_ 0.0;// 初始化cudaEventcheckCudaRuntime(cud…...
——双向循环链表)
数据结构【Golang实现】(四)——双向循环链表
目录0. 定义节点1. IsEmpty()2. Length()3. AddFromHead()4. AddFromTail()5. Insert()6. DeleteHead()7. DeleteTail()8. Remove()9. RemoveByValue()10. Contain()11. Traverse()0. 定义节点 type DLNode struct {Data anyPrev, Next *DLNode }// DoublyLoopLinkedLis…...
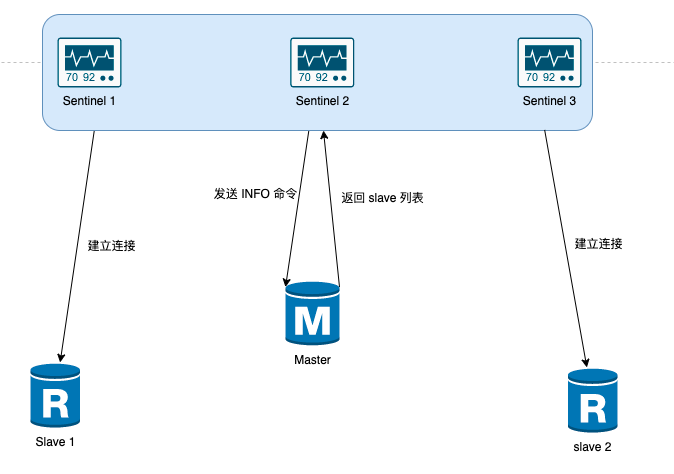
【Redis】高可用架构之哨兵模式 - Sentinel
Redis 高可用架构之哨兵模式 - Sentinel1. 前言2. Redis Sentinel 哨兵集群搭建2.1 一主两从2.2 三个哨兵3. Redis Sentinel 原理剖析3.1 什么哨兵模式3.2 哨兵机制的主要任务3.2.1 监控(1)每1s发送一次 PING 命令(2)PING 命令的回…...

图片的美白与美化
博主简介 博主是一名大二学生,主攻人工智能研究。感谢让我们在CSDN相遇,博主致力于在这里分享关于人工智能,c,Python,爬虫等方面知识的分享。 如果有需要的小伙伴可以关注博主,博主会继续更新的,…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
