代码随想录| 编辑距离
判断子序列[https://leetcode.cn/problems/is-subsequence/description/]
题意:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
思路:从动态规划, dp[i][j] 表示s的前i-1个元素和t的前j-1个元素相同的子序列元素的个数。
还要对dp初始化。dp[i][0] 表示在t空串的情况下,s的前i-1个字符串的相等的情况。 都设为0 ; dp[0][j] 表示在s为空串的情况下与s的前j-1个字符串相等的情况。
状态转移:
if(s[i-1] == t[j-1])
dp[i][j] = dp[i-1][j-1] +1 ; // 表示 个数加1 。
else
dp[i][j] = dp[i][j-1] ; // 表示现在的状态是s的前一个元素的状态。
不同子序列
题意:两个字符串s, t 统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
思路:dp[i][j] 表示在s的前i-1个字符的情况下,t的前j-1个字符出现的次数。
dp初始化:dp[i][0] 表示s的前i-1个字符,t空串出现的次数为1 。
dp[0][j]= 0 表示s为空串的情况 , t串出现的次数为0 。
因为有这样的例子: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
dp[i][j] = dp[i-1][j-1] + dp[i-1][j] ; // 由s的上一个字符来达到。
动态转移:
if(s[i-1] == t[j-1])
// 分别由上一个迭代的dp[i][j] 的个数和dp[i-1][j]表示删除掉s的当前遍历元素的个数组成。
dp[i][j] = dp[i-1][j-1] + dp[i-1][j] ;
else
dp[i][j] = dp[i-1][j] ;
代码
class Solution {
public:int numDistinct(string s, string t) {const int N = 1e3+10 ;// 可以映射为删除s的元素的方式使得s最后与t相等的个数vector<vector<uint64_t >> dp(s.size()+10 , vector<uint64_t>(t.size() + 10 , 0)) ; // dp[i][j] 表示在s的前i-1的子串(子序列)出现t的前j-1个子串的个数。 for(int i = 0 ; i < s.size() ;++ i){dp[i][0] = 1; // 表示s的前i-1个子串,如何删除达到空字符串。 }// dpfor(int j = 1 ; j < t.size() ; ++ j ){dp[0][j] = 0 ; // 表示空字符串无论如何删除都达到不了j的状态。 }for(int i=1 ; i<= s.size() ; ++ i)for(int j = 1 ; j <= t.size() ;++ j){if(s[i-1] == t[j-1]){dp[i][j] = dp[i-1][j-1] +dp[i-1][j] ; // 分别由上一个迭代的dp[i][j] 的个数和dp[i-1][j]表示删除掉s的当前遍历元素的个数组成。 }else{dp[i][j] = dp[i-1][j] ; }}for(int j = 0 ; j <= 3 ; ++ j){for(int i = 0 ; i <= 7 ; ++i){cout<<dp[i][j]<<" " ; }cout<<endl ; }return dp[s.size()][t.size()] ; }
};
两个字符串的删除操作
题意:给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
思路:dp[i][j] 表示word1在i-1和word2在j-1之前相同的最小步数。
动态转移:
当word1[i-1] == word2[j-1]
dp[i][j] = dp[i-1][j-1] ;
当word1[i-1] != word2[j-1]
dp[i][j] = min (dp[i-1][j] +1 , dp[i][j-1]+1 , dp[i-1][j-1] +2 ) ; // 包括删除word1这个i元素, 等于dp[i-1][j] 的状态 +1 加一表示加上删除操作。 dp[i][j-1] +1 ; 和表示dp[i-1][j] +1 和两个字符串 都要删除自己末尾的元素。
代码
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<uint64_t>> dp(word1.size()+10, vector<uint64_t>(word2.size()+10 , 0 )) ; // dp[i][j] 表示使word1的前i-1字符和word2的前j-1个字符的最小步数。 for(int i = 0 ; i <= word1.size() ; ++ i){dp[i][0] = i ; // 步数是i+1 删除i个字符串。 可以达到word2为空的状态。 }for(int j = 0 ; j <= word2.size() ; ++ j){dp[0][j] = j ; // 步数是j+1 ; 删除j个字符串, 可以达到word1为空的状态}for(int i = 1 ; i <= word1.size() ; ++ i)for(int j = 1 ; j <= word2.size() ; ++ j){if(word1[i-1] == word2[j-1]){dp[i][j] = dp[i-1][j-1] ; }else{dp[i][j] = min (dp[i-1][j] +1 ,min( dp[i][j-1] +1 , dp[i-1][j-1] +2 ) ) ; // 是要在dp[i-1 ] [j] 的状态下加1 。 和dp[i][j-1] 的状态下加1 或者 dp[i-1][j-1]的状态下加2中选一个最小的。 }}return dp[word1.size()][word2.size()] ; }
};
以上几个题是为最短编辑距离服务的
最短编辑距离:
给定两个单词word1和word2 。请返回将 word1 转换成 word2 所使用的最少操作数 。
- word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word2添加一个元素d,也就是相当于word1删除一个元素d,操作数大小一样!
思路:
dp[i][j] 表示在word1在i-1之前和 word2在j-1之前的最少操作次数。
如果word1[i-1] == word2[j-1] ; 那么
dp[i][j] =dp[i-1][j-1] ;
否则
dp[i][j] = min(dp[i-1][j] +1, dp[i][j-1] +1 , dp[i-1][j-1] +1 ) ; ; // dp[i-1][j-1] +1 表示修改 。
return dp[word1.size() ][word2.size()] ;
相关文章:

代码随想录| 编辑距离
判断子序列[https://leetcode.cn/problems/is-subsequence/description/] 题意:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 思路:从动态规划, dp[i][j] 表示s的前i-1个元素和t的前j-1个元素相同的子序列元素的个数。 还要对d…...

MOJO编程语言的编译与执行:深入编译器与解释器的工作原理
引言 MOJO编程语言以其面向对象的特性和简洁的语法而受到开发者的欢迎。在MOJO的世界中,编译器和解释器是两个核心组件,它们负责将MOJO代码转换为机器可执行的指令。本文将探讨MOJO编译器和解释器的工作原理,以及它们如何在MOJO编程过程中发…...

nginx-限制客户端并发数
文章目录 前言一、ngx_http_limit_conn_module二、指令介绍1. limit_conn_zone2.limit_conn3. limit_conn_log_level4. limit_conn_status 案例未限制限制 总结 前言 瞬时大量用户访问服务器,导致服务器超载而宕机。 恶意请求攻击服务器,导致服务器超载…...

Vatee万腾平台:智能生活的新选择
在科技飞速发展的今天,智能生活已经不再是遥不可及的梦想,而是逐渐渗透到我们日常生活的方方面面。Vatee万腾平台,作为智能科技领域的佼佼者,正以其创新的技术、丰富的应用场景和卓越的用户体验,成为智能生活的新选择&…...

白嫖A100-interLM大模型部署试用活动,亲测有效-2.Git
申明 以下部分内容来源于活动教学文档: Docs git 安装 是一个开源的分布式版本控制系统,被广泛用于软件协同开发。程序员的必备基础工具。 常用的 Git 操作 git init 初始化一个新的 Git 仓库,在当前目录创建一个 .git 隐藏文件夹来跟踪…...
LeetCode 60.排序排列(dfs暴力)
给出集合 [1,2,3,...,n],其所有元素共有 n! 种排列。 按大小顺序列出所有排列情况,并一一标记,当 n 3 时, 所有排列如下: "123""132""213""231""312""321" 给定…...

矩阵分析与应用1-矩阵代数基础
矩阵分析与应用1-矩阵代数基础 1 矩阵的基本运算2 矩阵的初等变换3 向量空间、线性映射与Hilbert空间4 内积与范数5 随机向量6 矩阵的性能指标7 逆矩阵与伪逆矩阵8 Moore-Penrose逆矩阵9 矩阵的直和与Hadamard积10 Kronecker积与Khatri-Rao积11 向量化与矩阵化12 稀疏表示与压缩…...

Vue的学习之生命周期
一、生命周期 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>Vue的学习</title><script src"vue.js" type"text/javascript" charset"utf-8"></script></head>&l…...
【MySQL】表的操作{创建/查看/修改/删除}
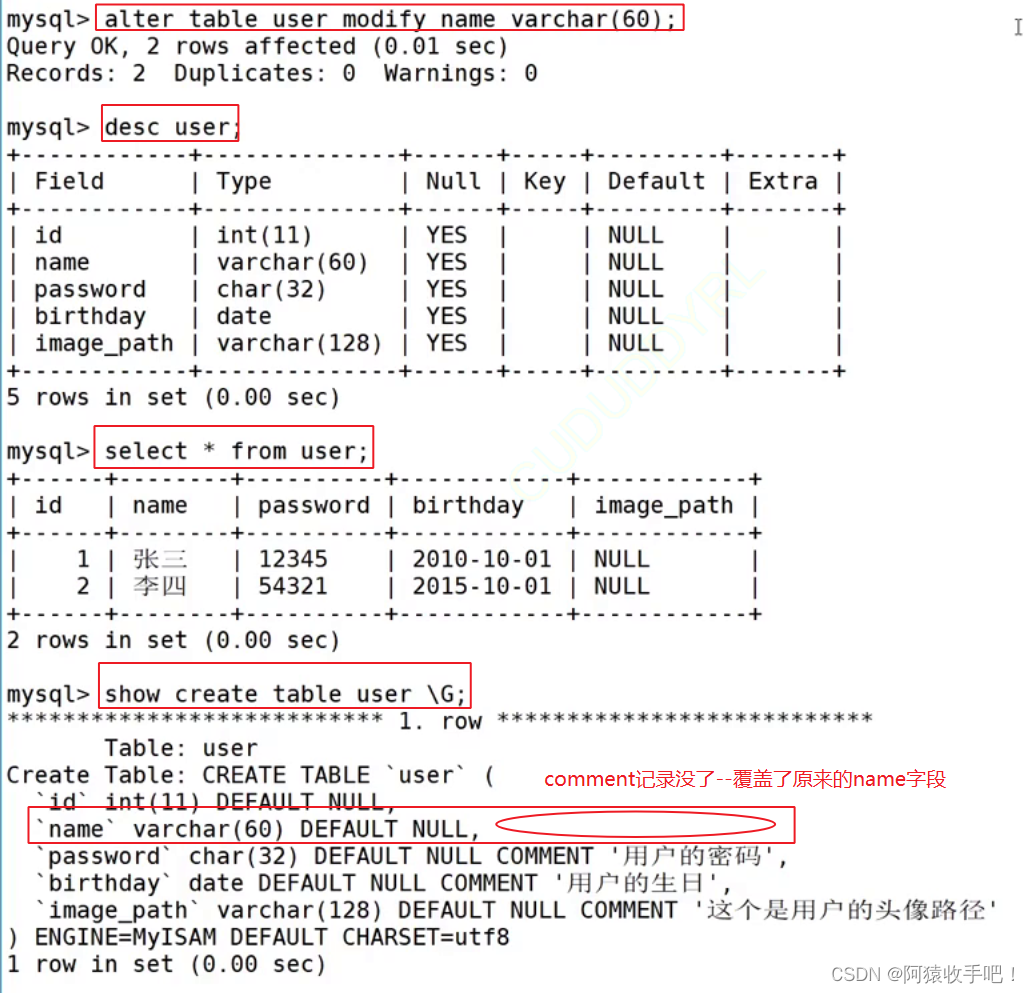
文章目录 1.创建表1.1comment:注释信息1.2存储引擎 2.查看表3.修改表3.1add添加列,对原数据无影响3.2drop删除列3.3modify修改列类型3.4change修改列名3.5rename [to]修改表名 4.删除表5.总结 1.创建表 CREATE TABLE table_name (field1 datatype,field…...

基于Python爬虫的城市二手房数据分析可视化
基于Python爬虫的城市二手房数据分析可视化 一、前言二、数据采集(爬虫,附完整代码)三、数据可视化(附完整代码)3.1 房源面积-总价散点图3.2 各行政区均价3.3 均价最高的10个小区3.4 均价最高的10个地段3.5 户型分布3.6 词云图四、如何更换城市一、前言 二手房具有价格普…...

这款新的 AI 语音助手击败了 OpenAI,成为 ChatGPT 最受期待的功能之一
OpenAI 推迟了 ChatGPT 令人印象深刻的语音模式,这让许多 AI 聊天机器人的粉丝感到不安,但他们现在可能已经被挖走了。法国人工智能开发商 Kyutai 推出了一款名为 Moshi 的实时语音 AI 助手。 Moshi 旨在通过语音(如 Alexa 或 Google Assista…...

CTS单测某个模块和测试项
1 ,测试单个模块命令 run cts -m <模块名> 比如:run cts -m CtsUsbTests模块名可以从测试报告中看,如下: 2, 测试单个测试项 run cts -m <模块名> -t <test_name> 比如:run cts -m ru…...

pytorch、pytorch_lightning、torchmetrics版本对应
目录 1.pytorch_lightning对应版本安装 2.PyTorch Lightning介绍 PyTorch Lightning 的作用: PyTorch Lightning 的基本用法: 报错:ModuleNotFoundError: No module named pytorch_lightning 这种报错一看就是缺了pytorch_lightning包&am…...

麒麟系统部署JeecgBoot
一、安装jdk 自带的即可,不必另外安装 二、安装MySQL 麒麟系统安装MySQL_麒麟系统安装万里数据库步骤-CSDN博客 三、安装Redis 麒麟系统安装Redis_麒麟上redis-CSDN博客 四、安装Nginx 1、下载 下载地址:https://redis.io/ 2、解压配置 tar .…...

要想贵人相助,首先自己得先成为贵人!
点击上方△腾阳 关注 转载请联系授权 在金庸江湖里,有两位大侠,一个是萧峰,一个是郭靖。 郭靖在《射雕英雄传》里是绝对的主角,在《神雕侠侣》当中也是重要的配角,甚至可以说是第二主角。 谈起郭靖,很多…...

使用块的网络 VGG
一、AlexNet与VGG 1、深度学习追求更深更大,使用VGG将卷积层组合为块 2、VGG块:3*3卷积(pad1,n层,m通道)、2*2最大池化层 二、VGG架构 1、多个VGG块后接全连接层 2、不同次数的重复块得到不同的架构&a…...

微信小程序性能与体验优化
1. 合理的设置可点击元素的响应区域大小; 比较常见的是页面的点击按钮太小,用户点击不到按钮,这样用户体验很不好。 2. 避免渲染页面耗时过长; 当页面渲染时间过长的话,会让用户感觉非常卡顿,当出现这种…...

Android14之获取包名/类名/服务名(二百二十三)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

FreeU: Free Lunch in Diffusion U-Net——【代码复现】
这篇文章发表于CVPR 2024,官网地址:ChenyangSi/FreeU: FreeU: Free Lunch in Diffusion U-Net (CVPR2024 Oral) (github.com) 一、环境准备 提前准备好python、pytorch环境 二、下载项目依赖 demo下有一个requirements.txt文件, pip inst…...

第三方商城对接重构(HF202407)
文章目录 项目背景一、模块范围二、问题方案1. 商品模块整体来说这块对接的不是太顺利,梳理了几条大概的思路: 2. 订单模块3. 售后4. 发票5. 结算单 经验总结 项目背景 作为供应商入围第三方商城成功,然后运营了一段时间,第三方通…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
