成人高考报名条件及收费标准详解
成人高考报名条件及收费标准详解
您想通过成人高考改变自己的命运,但不知道报名条件和收费标准?本文将为您详细介绍成人高考报名条件和收费标准,并为您提供专业的成人教育服务。
深圳成人高考www.shenzhixun.com

成人高考报名条件
成人高考报名条件主要包括三方面:年龄、学历和身体条件。
首先,年龄方面,报名者必须年满18周岁,具有完全民事行为能力。
其次,学历方面,报名者可以是高中毕业生、中专毕业生或同等学历的学生。
最后,身体条件方面,报名者必须身体健康,能够参加高考和学习。
成人高考收费标准
成人高考收费标准根据地区和学校的不同而异。一般来说,成人高考报名费为100-500元人民币,考试费为50-200元人民币。
深职训学校解决问题
您在成人高考报名和学习过程中遇到了问题?深职训学校为您提供专业的成人教育服务。
我们拥有经验丰富的教师和专业的教学设施,能够为您提供高质量的成人教育服务。
我们的成人高考报名服务包括:报名指导、考试培训、学习规划等。
同时,我们还提供了成人高考复习班,包括:课程设计、教学实施、学习监控等。
如果您在成人高考报名和学习过程中遇到了问题,随时找我们交流,我们很愿意听取并分享我们的经验。
深职训学校,您的成人教育合作伙伴。
相关文章:

成人高考报名条件及收费标准详解
成人高考报名条件及收费标准详解 您想通过成人高考改变自己的命运,但不知道报名条件和收费标准?本文将为您详细介绍成人高考报名条件和收费标准,并为您提供专业的成人教育服务。 深圳成人高考www.shenzhixun.com 成人高考报名条件 成人高考…...
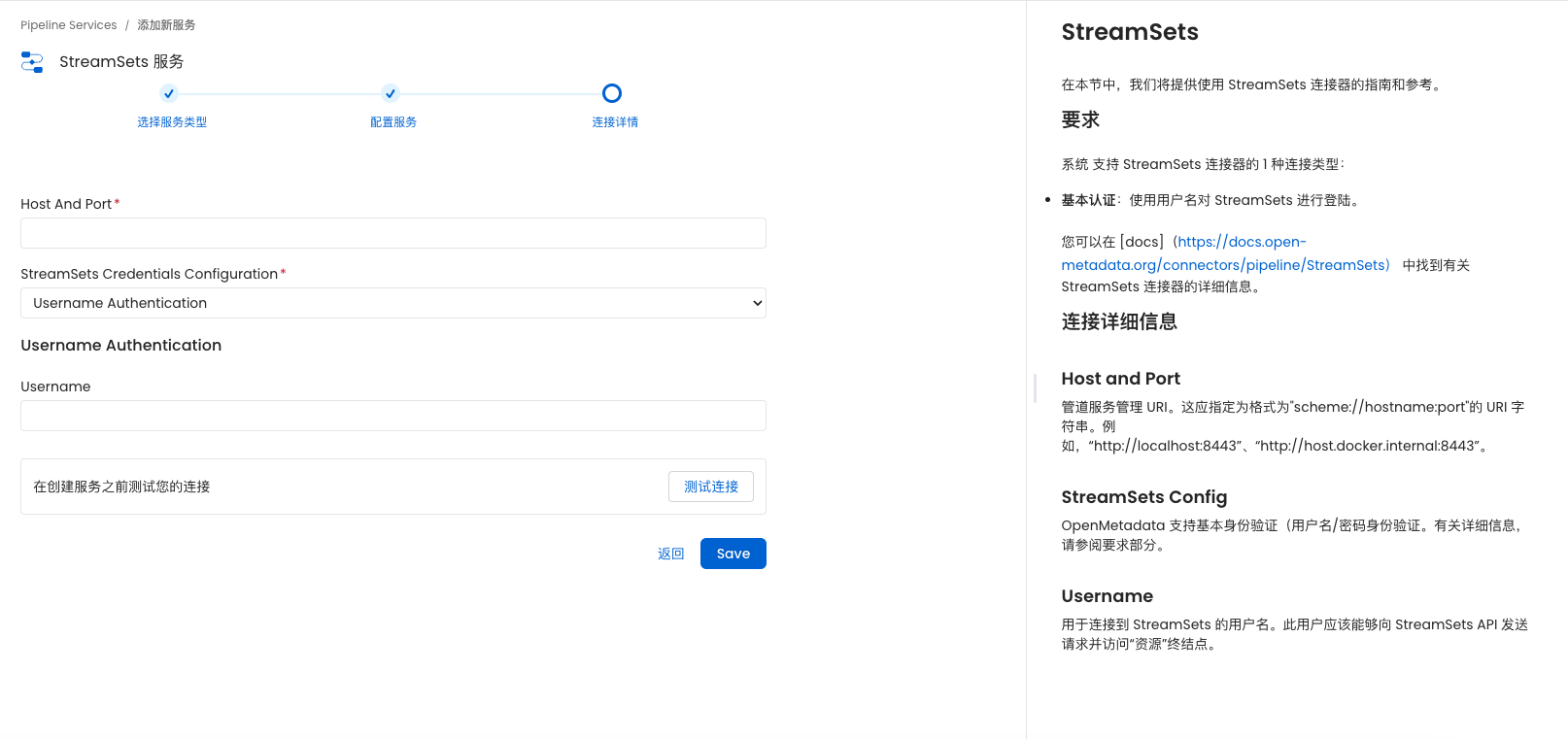
openmetadata1.3.1 自定义连接器 开发教程
openmetadata自定义连接器开发教程 一、开发通用自定义连接器教程 官网教程链接: 1.https://docs.open-metadata.org/v1.3.x/connectors/custom-connectors 2.https://github.com/open-metadata/openmetadata-demo/tree/main/custom-connector (一&…...

PostgreSQL 如何优化存储过程的执行效率?
文章目录 一、查询优化1. 正确使用索引2. 避免不必要的全表扫描3. 使用合适的连接方式4. 优化子查询 二、参数传递1. 避免传递大对象2. 参数类型匹配 三、减少数据量处理1. 限制返回结果集2. 提前筛选数据 四、优化逻辑结构1. 分解复杂的存储过程2. 避免过度使用游标 五、事务处…...

普中51单片机:数码管显示原理与实现详解(四)
文章目录 引言数码管的结构数码管的工作原理静态数码管电路图开发板IO连接图代码演示 动态数码管实现步骤数码管驱动方式电路图开发板IO连接图真值表代码演示1代码演示2代码演示3 引言 数码管(Seven-Segment Display)是一种常见的显示设备,广…...
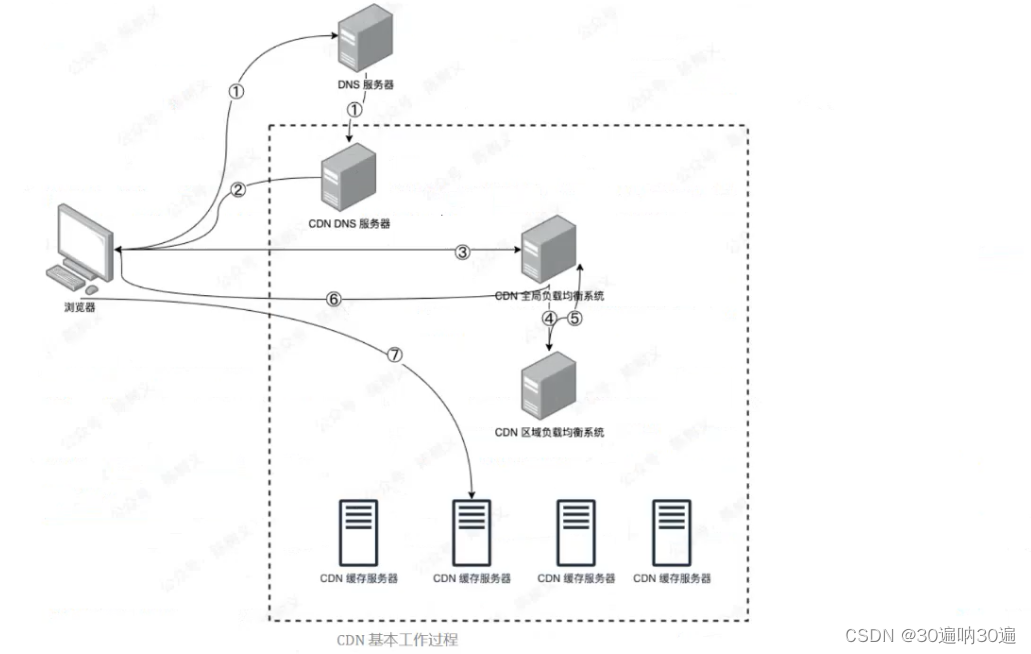
web缓存代理服务器
一、web缓存代理 web代理的工作机制 代理服务器是一个位于客户端和原始(资源)服务器之间的服务器,为了从原始服务器取得内容,客户端向代理服务器发送一个请求,并指定目标原始服务器,然后代理服务器向原始…...

容器:queue(队列)
以下是关于queue容器的总结 1、构造函数:queue [queueName] 2、添加、删除元素: push() 、pop() 3、获取队头/队尾元素:front()、back() 4、获取栈的大小:size() 5、判断栈是否为空:empty() #include <iostream> #include …...

探索 WebKit 的后台同步新纪元:Web Periodic Background Synchronization 深度解析
探索 WebKit 的后台同步新纪元:Web Periodic Background Synchronization 深度解析 随着 Web 应用逐渐成为我们日常生活中不可或缺的一部分,用户对应用的响应速度和可靠性有了更高的期待。Web Periodic Background Synchronization API(周期…...

ctfshow web入门 web338--web344
web338 原型链污染 comman.js module.exports {copy:copy };function copy(object1, object2){for (let key in object2) {if (key in object2 && key in object1) {copy(object1[key], object2[key])} else {object1[key] object2[key]}}}login.js var express …...

mupdf加载PDF显示中文乱码
现象 加载PDF显示乱码,提示非嵌入字体 non-embedded font using identity encoding调式 在pdf-font.c中加载字体 调试源码发现pdf文档的字体名字居然是GBK,估计又是哪个windows下写的pdf生成工具生成pdf 字体方法: static pdf_font_desc * load_cid…...

常用的限流工具Guava RateLimiter 或Redisson RRateLimiter
在分布式系统和高并发场景中,限流是一个非常常见且重要的需求。以下是一些常用的限流工具和库,包括它们的特点和使用场景: 1. Guava RateLimiter Google 的 Guava 库中的 RateLimiter 是一个简单且高效的限流工具,适用于单节点应…...
和循环神经网络(RNN) 的区别与联系)
卷积神经网络(CNN)和循环神经网络(RNN) 的区别与联系
卷积神经网络(CNN)和循环神经网络(RNN)是两种广泛应用于深度学习的神经网络架构,它们在设计理念和应用领域上有显著区别,但也存在一些联系。 ### 卷积神经网络(CNN) #### 主要特点…...

Unity【入门】场景切换和游戏退出及准备
1、必备知识点场景切换和游戏退出 文章目录 1、必备知识点场景切换和游戏退出1、场景切换2、鼠标隐藏锁定相关3、随机数和自带委托4、模型资源的导入1、模型由什么构成2、Unity支持的模型格式3、如何指导美术同学导出模型4、学习阶段在哪里获取模型资源 2、小项目准备工作需求分…...

Python 函数递归
以下是一个使用递归计算阶乘的 Python 函数示例 : 应用场景: 1. 动态规划问题:在一些需要逐步求解子问题并利用其结果的动态规划场景中,递归可以帮助直观地表达问题的分解和求解过程。 2. 遍历具有递归结构的数据:如递…...
如何配置 MyBatis 实现打印可执行的 SQL 语句)
MyBatis(27)如何配置 MyBatis 实现打印可执行的 SQL 语句
在开发过程中,打印可执行的SQL语句对于调试和性能优化是非常有帮助的。MyBatis提供了几种方式来实现SQL语句的打印。 1. 使用日志框架 MyBatis可以通过配置其内部使用的日志框架(如Log4j、Logback等)来打印SQL语句。这是最常用的方法。 Lo…...

3.js - 裁剪平面(clipIntersection:交集、并集)
看图 代码 // ts-nocheck// 引入three.js import * as THREE from three// 导入轨道控制器 import { OrbitControls } from three/examples/jsm/controls/OrbitControls// 导入lil.gui import { GUI } from three/examples/jsm/libs/lil-gui.module.min.js// 导入tween import …...

在5G/6G应用中实现高性能放大器的建模挑战
来源:Modelling Challenges for Enabling High Performance Amplifiers in 5G/6G Applications {第28届“集成电路和系统的混合设计”(Mixed Design of Integrated Circuits and Systems)国际会议论文集,2021年6月24日至26日,波兰洛迪} 本文讨…...

Perl 数据类型
Perl 数据类型 Perl 是一种功能丰富的编程语言,广泛应用于系统管理、网络编程、GUI 开发等领域。在 Perl 中,数据类型是编程的基础,决定了变量存储信息的方式以及可以对这些信息执行的操作。本文将详细介绍 Perl 中的主要数据类型࿰…...

网络协议 -- IP、ICMP、TCP、UDP字段解析
网络协议报文解析及工具使用介绍 1. 以太网帧格式及各字段作用 -------------------------------- | Destination MAC Address (48 bits) | -------------------------------- | Source MAC Address (48 bits) …...

【工具】豆瓣自动回贴软件
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 相比于之前粗糙丑陋的黑命令框版本,这个版本新增了UI界面,从此可以不需要再挨个去翻配置文件了。 另外,升级了隐藏浏…...

初学Spring之动态代理模式
动态代理和静态代理角色一样 动态代理的代理类是动态生成的 动态代理分为两大类: 基于接口的动态代理(JDK 动态代理)、基于类的动态代理(cglib) 也可以用 Java 字节码实现(Javassist) Prox…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
