【算法专题】双指针算法
1. 移动零
题目分析
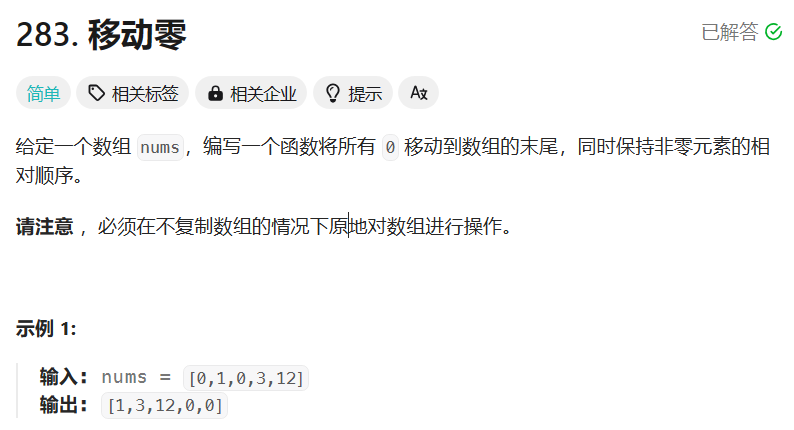
对于这类数组分块的问题,我们应该首先想到用双指针的思路来进行处理,因为数组可以通过下标进行访问,所以说我们不用真的定义指针,用下标即可。比如本题就要求将数组划分为零区域和非零区域,我们不妨定义两个指针cur和dest,cur不断向后遍历,dest则指向已处理区间内最后一个非零元素,当cur找到一个非零元素时,就把dest++并交换dest和cur对应的数组元素
那么在处理数组的过程中,数组被划分为了三块区域:
[0, dest] [dest+1, cur] [cur+1, n-1]
分别代表:非零区域、零区域、未处理区域
当处理结束后只剩下非零区域和零区域了,而我们也实现了题目的要求,把数组中的所有元素都移动到数组末尾,且不改变其他元素的次序
实现代码:
class Solution {
public:void moveZeroes(vector<int>& nums) {int dest = -1, cur = 0; // 我们一开始并不知道dest的位置,暂时定义为-1while(cur < nums.size()) {if(nums[cur] == 0) {cur++;}else if(nums[cur] != 0) {dest++;swap(nums[dest], nums[cur]);cur++;}}}
};2. 复写零
1089. 复写零 - 力扣(LeetCode)

题目描述:
依据题意,数组中的零是会被重复写一遍的,那么一旦数组中有0,数组后面肯定就会有元素被覆盖掉,所以我们肯定是不能从前向后进行处理的。
为了保证不漏掉元素,我们应该要找到最后一个没有被覆盖的元素,然后把这个元素填到数组最后面,接着向前遍历,如果碰到的元素是非零,就填一次,如果是零就填两次,这样就实现了把所有的零都复写一遍,显然这个过程我们还是需要两个指针来帮助我们完成覆盖的操作。
所以我们接下来要实现的就是:
1. 找到最后一个“复写”的数
两个指针cur和dest,cur向后遍历,当碰到0时,dest向后移动两位,否则向后移动一位,这样,当dest指向数组末尾时,cur指向的位置就是数组中最后一个需要复写的元素位置了
2. 从前向后进行复写
在第一步处理之后,dest指向了数组末尾,cur指向了最后一个要复写的下标,cur和dest开始从后往前移动,并把cur元素覆盖到dest位置上,如果cur元素为0,就覆盖两次
3. 边界情况
一般情况下,上述的第一步处理中,dest是能正常移动到n-1位置的,但是存在这样一种情况:
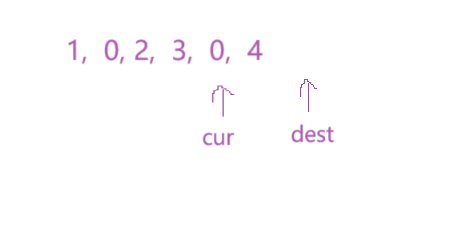
当数组内容如上所示时,第一步的操作就会出现问题,dest指向了数组长度之外的位置,我们需要对这种情况进行特殊处理
实现代码:
class Solution {
public:void duplicateZeros(vector<int>& arr) {int cur = 0, dest = -1;int n = arr.size();while(cur <= n - 1) // 找到最后一个复写元素{if(arr[cur]) dest++;else dest += 2;if(dest >= n - 1){break;}cur++;}if(dest == n) // 对特殊情况进行处理{arr[n - 1] = 0;cur--;dest -= 2;}while(cur >= 0) // 从后往前进行复写{if(arr[cur]) arr[dest--] =arr[cur--];else{arr[dest--] = 0;arr[dest--] = 0;cur--;}}}
};3. 快乐数
202. 快乐数 - 力扣(LeetCode)

题目分析
依题意,对于一个正整数,如果每次将其替换为每个位置上数字的平方和,那么这个数最终可能为1或进入无限循环。事实上,这一点我们是可以证明的,首先给大家讲一下鸽巢原理:如果有n个巢穴,n+1只鸽子,那么至少有一个巢穴是有两只鸽子的。然后接下来解决本题,n的范围如上,如果将其最大值替换为每个位置上数字的平方和,2^31-1 的值为2,147,483,647,就算把这十位数换成9,999,999,999,按照这个算法,结果也只有810。
也就是说,本题n取值范围内的所有数,经过处理得到的结果都不超过810,所以只要n经过811次变换,最后一定至少出现一次重复的元素,也就进入了循环。原因是:前810次n已经将所有变换的可能结果枚举了一遍,第811次的结果必定在前810次变换结果的集合之中,所以必定重复。
算法原理
经过上述证明,我们清楚了n经过足够多次数的变换,只可能进入重复循环或变为1,而1的平方和恒为1,也算一个循环。所以我们要判断一个数是不是快乐数,只需要判断在循环中,这个数是不是1即可。
这就要用到快慢指针算法了,fast指针一次移动两个单位,slow指针一次移动一个单位,则一旦fast和slow相遇,就说明已经在循环中了,此时仅需判断相遇时值是否为1即可。
代码如下:
class Solution {
public:// 进行变换int getsum(int n) {int sum = 0;while(n) {int tmp = n % 10;sum += tmp * tmp;n /= 10;}return sum;}bool isHappy(int n) {int fast = n, slow = n;do {// fast每次移动两个单位,slow移动一个单位fast = getsum(getsum(fast));slow = getsum(slow);} while(fast != slow);// 最后仅需判断相遇时值是否为1return fast == 1;}
};4. 盛水最多的容器
11. 盛最多水的容器 - 力扣(LeetCode)
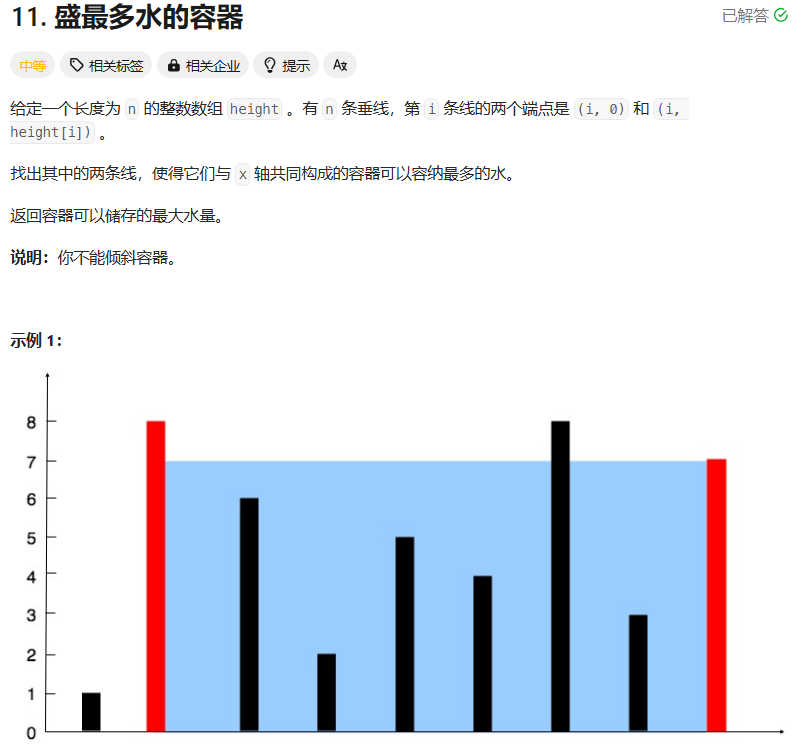

题目解析
根据题目示例,我们发现容器高度是由两端的柱子中较短的一根所决定的,设其高度为h,两根柱子的距离设为l,则我们要找的就是h*l最大的组合
算法原理
解法一 暴力解法
从起始位置开始,将所有的位置都枚举一遍,最后肯定能找到盛水最多的容器,时间复杂度是O(n^2)但这样做肯定是会超时的,我们必须想一种更优秀的方法
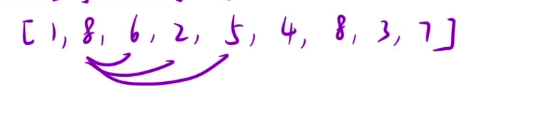
解法二 双指针算法

我们先用一个小区间来举例子,在题目解析中,我们看出了,容器高度由两端中较短的一方决定。在这个例子中,如果我们固定较短的柱子,移动另一端,可以发现,容器的容积是在减小的,问题在于:
1. 向内枚举,区间长度是一定减小的
2. 固定了短端,移动另一端,如果另一端比短端短,高度减小;就算比短端长,高度也不会变大
所以趋势是:l一定减小,h不变或减小,v = h * l,则容积也必定减小!
而如果我们固定较长的柱子,移动另一端,情况则有不同,如果短端找到更长的柱子,容器的容积是有可能增大的
所以我们可以定义两个指针left、right在区间的0和n-1位置,找到短的一方,计算出当前容积,移动长的一方,这样我们只需要遍历数组一遍就能够找到最大值,时间复杂度为O(n)
class Solution {
public:int maxArea(vector<int>& height) {int l = 0, r = height.size() - 1;int h, w;int v = 0;while(l != r) {h = height[l] < height[r] ? height[l] : height[r];w = r - l;int tmp = h * w;v = tmp > v ? tmp : v;if(height[l] < height[r]) l++;else r--;}return v;}
};5. 有效三角形的个数
611. 有效三角形的个数 - 力扣(LeetCode)

题意分析:
我们都知道,三角形的三条边满足任意两条边之和大于第三条边,但是还有一个更进一步的结论:假设a < b < c,则只要三个数满足a + b > c,就能保证任意两边之和大于第三条边。
因此本题就转化为了,找到数组中满足 a < b < c 且 a + b > c 的三元组个数。
算法原理:
解法一:暴力解法
用三层for循环列举出所有的三元组,然后判断是否满足构成三角形的条件,则时间复杂度:3*n^3,进行一下优化,如果我们先把数组排序,那么判断是否满足条件就只需要一次,时间复杂度为:n*logn + n^3,显然时间复杂度还是O(n^3),肯定是会超时的,我们需要想办法减小时间复杂度。
解法二:双指针算法
在前面我们分析过了,要找的是满足 a < b < c 且 a + b > c 的三元组个数,和解法一中的优化一样,我们先将数组进行排序,则c肯定就在数组的末端找了,所以我们不妨先固定c,再找符合条件的a、b即可。
可是如果我们还是用遍历的方式去找a和b,那时间复杂度根本就没有降低,还是O(n^3),所以必须换一个思路,既然 a < b ,我们不妨定义两个指针:left,right,分别从数组左右端移动,与上一道题类似的,我们要通过单调性来决定是移动left还是right!
如果 a + b > c,因为数组排过序,是单调递增的,left++过程中是始终满足 a + b > c 的,由于本题求的是三元组个数,没必要进行left++了,直接right - left求个数即可。之后我们再进行right--,当left == right时,说明这个c为最长边的情况列举完了,接着求下一个c为最长边的情况。
如果 a + b <= c,因为数组排过序,是单调递增的,如果我们让right--,a + b 只能更小,因此只能让left++,直到 a + b > c 或 left == right。
代码如下:
class Solution {
public:int triangleNumber(vector<int>& nums) {int a, b, c;int max = nums.size() - 1;int cnt = 0;sort(nums.begin(), nums.end());while(max > 1){int left = 0, right = max - 1;while(left != right){a = nums[left], b = nums[right], c = nums[max];if(a + b > c){cnt += right - left;right--;}else left++;}max--;}return cnt;}
};相关文章:

【算法专题】双指针算法
1. 移动零 题目分析 对于这类数组分块的问题,我们应该首先想到用双指针的思路来进行处理,因为数组可以通过下标进行访问,所以说我们不用真的定义指针,用下标即可。比如本题就要求将数组划分为零区域和非零区域,我们不…...

Lock与ReentrantLock
在 Java 中,Lock 接口和 ReentrantLock 类提供了比使用 synchronized 方法和代码块更广泛的锁定机制。 简单示例: import java.util.concurrent.locks.Lock; import java.util.concurrent.locks.ReentrantLock;public class ReentrantLockExample {pr…...
:紫光同芯嵌入式)
ARM/Linux嵌入式面经(十三):紫光同芯嵌入式
static关键字 static关键字一文搞懂这个知识点,真的是喜欢考!!! stm32启动时如何配置栈的地址 在STM32启动时配置栈的地址是一个关键步骤,这通常是在启动文件(如startup_stm32fxxx.s,其中xxx代表具体的STM32型号)中完成的。 面试者回答: STM32启动时配置栈的地址主…...
—— 说说你空窗期做了什么?)
名企面试必问30题(二十四)—— 说说你空窗期做了什么?
回答示例一 在空窗期这段时间,我主要进行了两方面的活动。 一方面,我持续提升自己的专业技能。我系统地学习了最新的软件测试理论和方法,深入研究了自动化测试工具和框架,例如 Selenium、Appium 等,并通过在线课程和实…...

基础权限储存
一、要求: 1、建立用户组shengcan,其id为2000工 2、建立用户组 caiwu,其id为2001 3、建立用户组 jishu,其id 为 2002 4、建立目录/sc,此目录是 shengchan 部门的存储目录,只能被 shengchan 组的成员操作,其他用户没有…...

Could not find a package configuration file provided by “roscpp“ 的参考解决方法
文章目录 写在前面一、问题描述二、解决方法参考链接 写在前面 自己的测试环境: Ubuntu20.04 ROS-Noetic 一、问题描述 编译程序时出现如下报错: -- Could NOT find roscpp (missing: roscpp_DIR) -- Could not find the required component roscpp.…...

运维系列.Nginx配置中的高级指令和流程控制
运维专题 Nginx配置中的高级指令和流程控制 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/…...

Virtualbox和ubuntu之间的关系
1、什么是ubuntu Ubuntu 是一个类似于 Windows 的操作系统,但它是基于 Linux 内核开发的开源操作系统 2、什么是Virtualbox VirtualBox 是一款虚拟机软件,使我们可以物理机上创建和运行虚拟机 也就是说,VirtualBox 提供了一个可以安装和运行其他操作系…...

【在Linux世界中追寻伟大的One Piece】HTTPS协议原理
目录 1 -> HTTPS是什么? 2 -> 相关概念 2.1 -> 什么是"加密" 2.2 -> 为什么要加密 2.3 -> 常见的加密方式 2.4 -> 数据摘要 && 数据指纹 2.5 -> 数字签名 3 -> HTTPS的工作过程 3.1 -> 只使用对称加密 3.2 …...
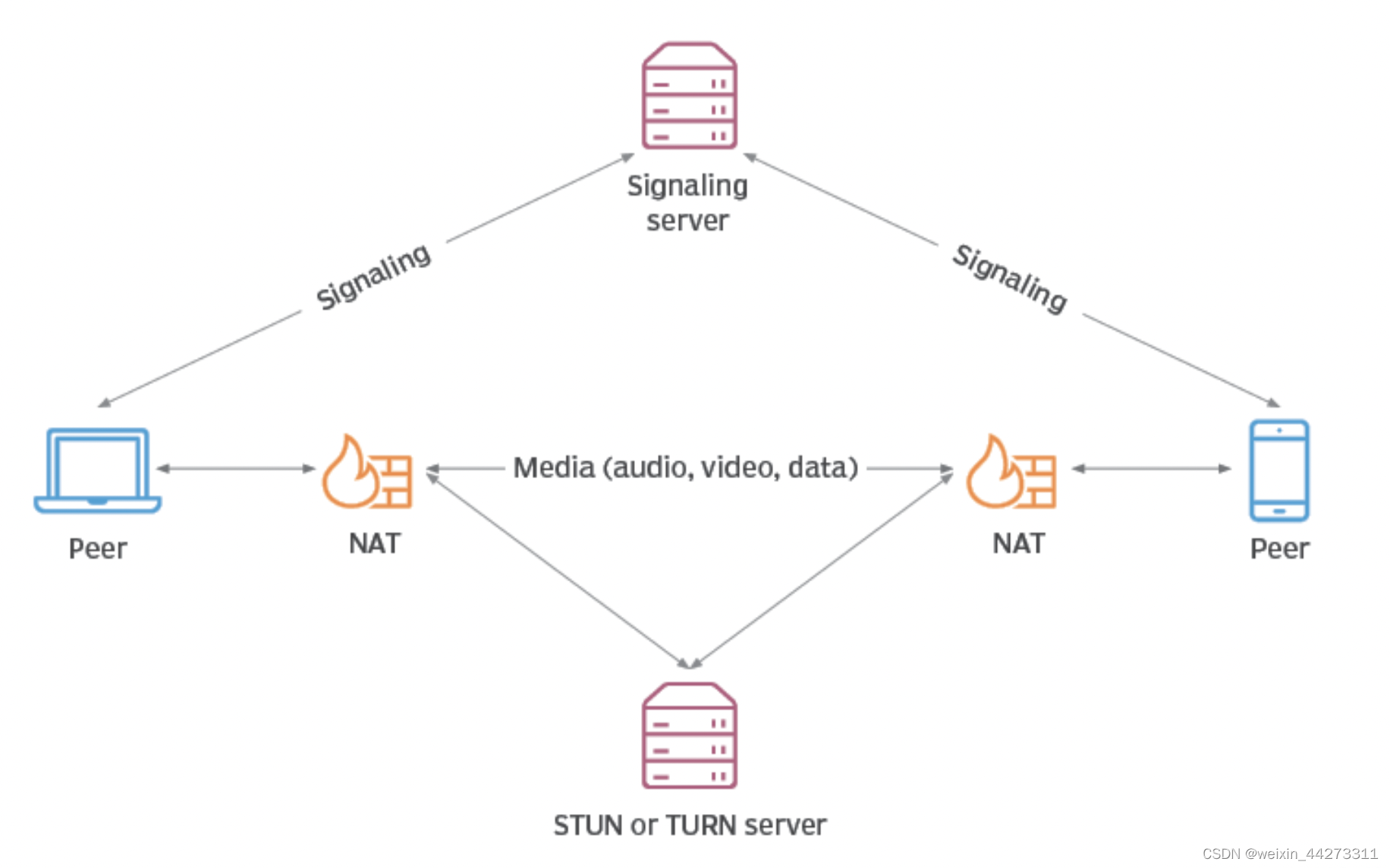
【WebRTC实现点对点视频通话】
介绍 WebRTC (Web Real-Time Communications) 是一个实时通讯技术,也是实时音视频技术的标准和框架。简单来说WebRTC是一个集大成的实时音视频技术集,包含了各种客户端api、音视频编/解码lib、流媒体传输协议、回声消除、安全传输等。对于开发者来说可以…...

【Unity】RPG2D龙城纷争(八)寻路系统
更新日期:2024年7月4日。 项目源码:第五章发布(正式开始游戏逻辑的章节) 索引 简介一、寻路系统二、寻路规则(角色移动)三、寻路规则(角色攻击)四、角色移动寻路1.自定义寻路规则2.寻…...

C++ 函数高级——函数重载——基本语法
作用:函数名可以相同,提高复用性 函数重载满足条件: 1.同一个作用域下 2.函数名称相同 3.函数参数类型不同 或者 个数不同 或者 顺序不同 注意:函数的返回值不可以作为函数重载的条件 示例: 运行结果:...

Go语言实现的端口扫描工具示例
Go语言实现的端口扫描工具示例 创建一个端口扫描工具涉及到网络编程和并发处理,下面是一个简单的Go语言实现的端口扫描工具示例。这个工具会扫描指定IP地址的指定范围内的端口。 请注意,使用端口扫描工具可能会违反某些网络的使用条款,甚至…...

SpringSecurity初始化过程
SpringSecurity初始化过程 SpringSecurity一定是被Spring加载的: web.xml中通过ContextLoaderListener监听器实现初始化 <!-- 初始化web容器--><!--设置配置文件的路径--><context-param><param-name>contextConfigLocation</param-…...

Python爬取股票信息-并进行数据可视化分析,绘股票成交量柱状图
为了使用Python爬取股票信息并进行数据可视化分析,我们可以使用几个流行的库:requests 用于网络请求,pandas 用于数据处理,以及 matplotlib 或 seaborn 用于数据可视化。 步骤 1: 安装必要的库 首先,确保安装了以下P…...

秋招突击——7/4——复习{}——新作{最长公共子序列、编辑距离、买股票最佳时机、跳跃游戏}
文章目录 引言复习新作1143-最长公共子序列个人实现 参考实现编辑距离个人实现参考实现 贪心——买股票的最佳时机个人实现参考实现 贪心——55-跳跃游戏个人实现参考做法 总结 引言 昨天主要是面试,然后剩下的时间都是用来对面试中不会的东西进行查漏补缺ÿ…...
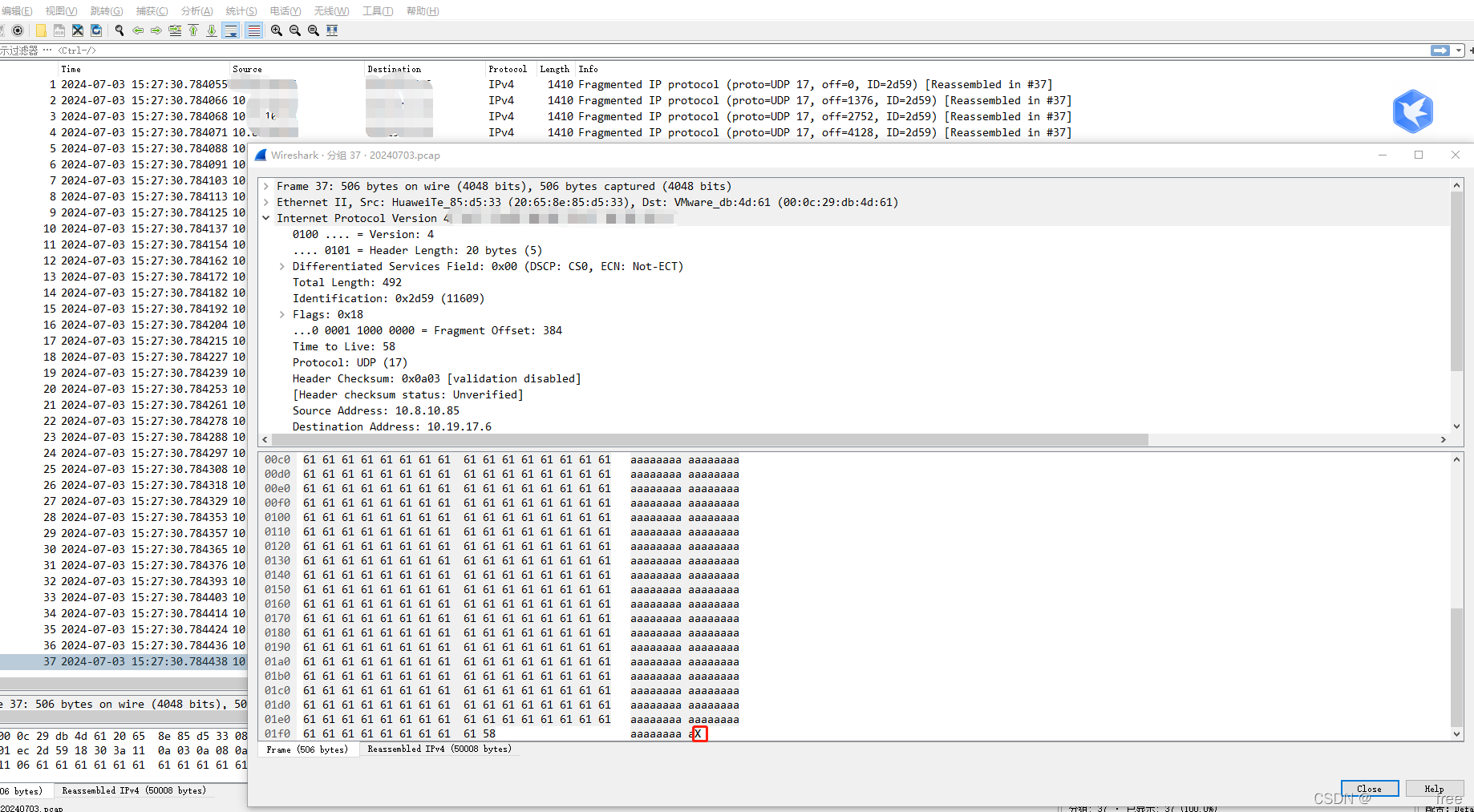
udp发送数据如果超过1个mtu时,抓包所遇到的问题记录说明
最近在测试Syslog udp发送相关功能,测试环境是centos udp头部的数据长度是2个字节,最大传输长度理论上是65535,除去头部这些字节,可以大概的说是64k。 写了一个超过64k的数据(随便用了一个7w字节的buffer)发送demo,打…...

电子电气架构 --- 智能座舱万物互联
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

笔记本电脑内存不够
笔记本电脑内存不够是众多笔记本用户面临的常见问题,尤其是对于一些需要处理大型文件或者运行复杂软件的用户,这个问题可能会严重影响笔记本的使用体验。那么,我们应该如何解决笔记本电脑内存不够的问题呢?本文将从几个方面进行详…...

Vue项目使用mockjs模拟后端接口
文章目录 操作步骤1. 安装 mockjs 和 vite-plugin-mock2. 安装 axios3. 创建mock路径4. 配置 viteMockConfig5. 编写第一个mock接口6. 创建 createProdMockServer7. 配置 axios8. 编写请求接口9. 在页面中使用 操作步骤 1. 安装 mockjs 和 vite-plugin-mock vite-plugin-mock …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
