简介空间复杂度
我们承接上一篇博客。我们写了时间复杂度之后,我们就要来介绍一下另一个相关复杂度了。空间复杂度。我觉得大家应该对空间复杂度认识可能比较少一些。我就是这样,我很少看见题目中有明确要求过空间复杂度的。但确实有这个是我们不可忽视的,所以我们要来学习和了解一下。
空间复杂度的含义
我们还是老样子,对于空间复杂度的含义,我们先用官方的解释来看一下:空间复杂度 (Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S (n)=O (f (n))。 比如直接 插入排序 的 时间复杂度 是O (n^2),空间复杂度是O (1) 。 而一般的递归算法就要有O (n)的空间复杂度了,因为每次递归都要存储返回信息。这是比较官方的解释了如果换成白话就是:空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。 就是一个代码在运行时需要临时创建的空间。可以理解为我原本只创建了40个字节的空间。然后再后面代码运行需要的时候又创建出来的空间大小,那么这就是空间复杂度了。当然有很多题在最开始创建的时候就给你确定的空间大小不能超过多少多少。所以我们这也是需要了解空间复杂度的必要性。
然后对于空间复杂度来说也是用大O表示法来表示的。并且因为前面已经讲过大O表示法了,那么我们这里就不在赘述了。接下来我们就还是直接来讲述一下如何计算空间复杂多了。
举例解释空间复杂度
示例1:
我们先来看一下我们上一篇博客也引用过就是冒泡排序。我们这里就来看看冒泡排序的空间复杂度是多少:
我们在前面说过空间复杂度是计算我们在代码运行时需要临时创建的空间大小,那么就是我们的空间复杂度。
我们看看冒泡排序的我们可以看一下这里它是否有重新创建一个新的空间?好像没有吧?因为这里面最多只是用那个是swap,就算是swap。他在内部重新创建了一个空间的话,那么也是个固定的,因为我们每次都可以直接重复利用,那么是不是我们这个冒泡排序的空间复杂度为零或者为一个常数? 然而我们在前面大o表示法中提及过,如果为常数的话,那么我们用大多表示法是不是都为O(1)。我们可以看到我们冒泡排序的空间复杂度和时间复杂度都为O(1)。所以大家也不要认为空间复杂度和时间复杂度是不相同的。
示例2:
接下来我们用的第二个例子就是我们上一篇也使用过的斐波那契数列。当然与上一篇博客的系数是有一点不相同的。因为我们要计算它的空间复杂度,所以稍微改变了一下,大家可以先看一下下面的照片,大概尝试着计算出这个代码的空间复杂度是多少?
我们可以看到这个代码里面在代码开头的时候就已经创建了一个空间了。在下面的for循环里面,我们对它的空间重新利用了一下。我们就在他后面都是创建新的空间。我们看一看这个。循环需要创建多少?是不是最主要的是就是我们的n。我们只需要确定了n的大小,那么我们就确定了我们还需要创建的空间大小了。然后我们也在前面说过大O表示法取最坏的结果。那么这个空间复杂度大家认为是多少呢?答案显而易见就是O(n)了。
示例3:
接下来我们再举一个例子,我相信大家就对空间复杂度的计算很了解了。上面我们也讲过递归的时间复杂度是如何计算的,那么接下来我们就计算递归的空间复杂度是如何计算的?
我们,大家来看一下这个递归。我们看递归嘛。肯定是会创建一个新的空间的。这里的递归是比较简单的,只创建一个。每一次都会创建一个,那么我们的这个递归是不是就是n啊。递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N) ?
这个递归是比较简单的,很容易看出它的空间复杂度是多少。我们的空间反度其实相对的话使用的比较少,除非一些考官在面试的时候会专门挑刺来考你。
总结
主要是大家需要了解一下和大概知道空间复杂度是如何计算的,这样就可以了。因为对于空间复杂度要求的话,其实题目还算比较少的,也像我们上面说过,除了一些在面试的时候需要考虑的话,至少我现在个人很少遇见对空间复杂度有要求的。总之大家还是需要了解一下如何计算嘛,然后这里就是今天这篇博客想与大家分享的吧。当然还有很多遗漏的东西,希望大家可以在评论区留言,然后我好补充。
相关文章:

简介空间复杂度
我们承接上一篇博客。我们写了时间复杂度之后,我们就要来介绍一下另一个相关复杂度了。空间复杂度。我觉得大家应该对空间复杂度认识可能比较少一些。我就是这样,我很少看见题目中有明确要求过空间复杂度的。但确实有这个是我们不可忽视的,所…...

windows server2016搭建AD域服务器
文章目录 一、背景二、搭建AD域服务器步骤三、生成可供java程序使用的keystore文件四、导出某用户的keytab文件五、主机配置hosts文件六、主机确认是否能ping通本人其他相关文章链接 一、背景 亲测可用,之前搜索了很多博客,啥样的都有,就是不介绍报错以…...
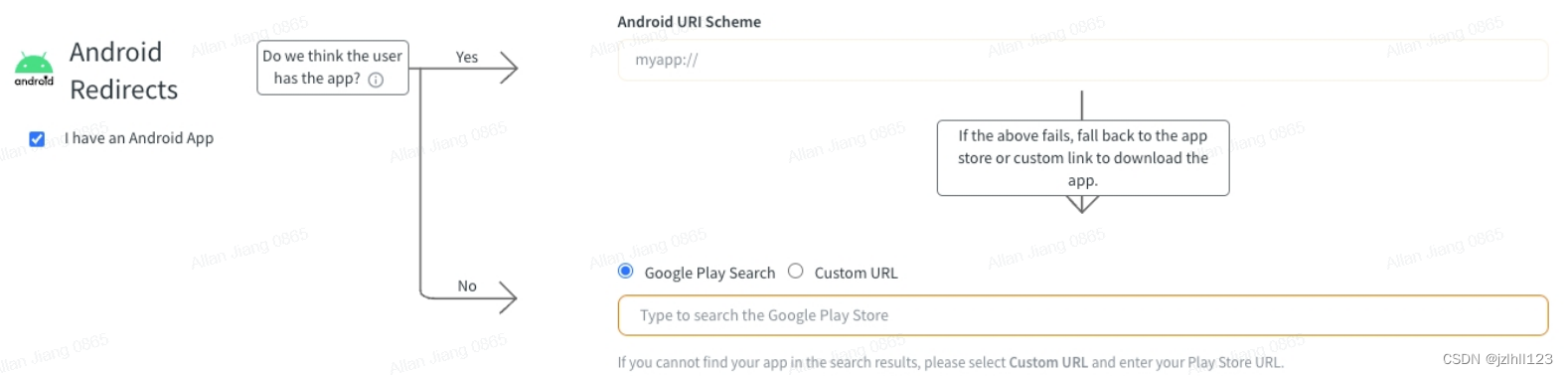
android deep links即scheme uri跳转以及googlePlay跳转配置
对于googlePlay的Custom URL就是googlePlay上APP网址: https://play.google.com/store/apps/details?idcom.yourapp如果是国内一些应用,则考虑market://包名等方式,自行百度。 对于Android URI Scheme: 首先需要在Manifest xm…...

QT5.14.2与Mysql8.0.16配置笔记
1、前言 我的QT版本为 qt-opensource-windows-x86-5.14.2。这是QT官方能提供的自带安装包的最近版本,更新的版本需要自己编译源代码,可点击此链接进行下载:Index of /archive/qt/5.14/5.14.2,选择下载 qt-opensource-windows-x86…...

判断是否为完全二叉树
目录 分析 分析 1.完全二叉树的概念:对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。 2.思路:可以采…...
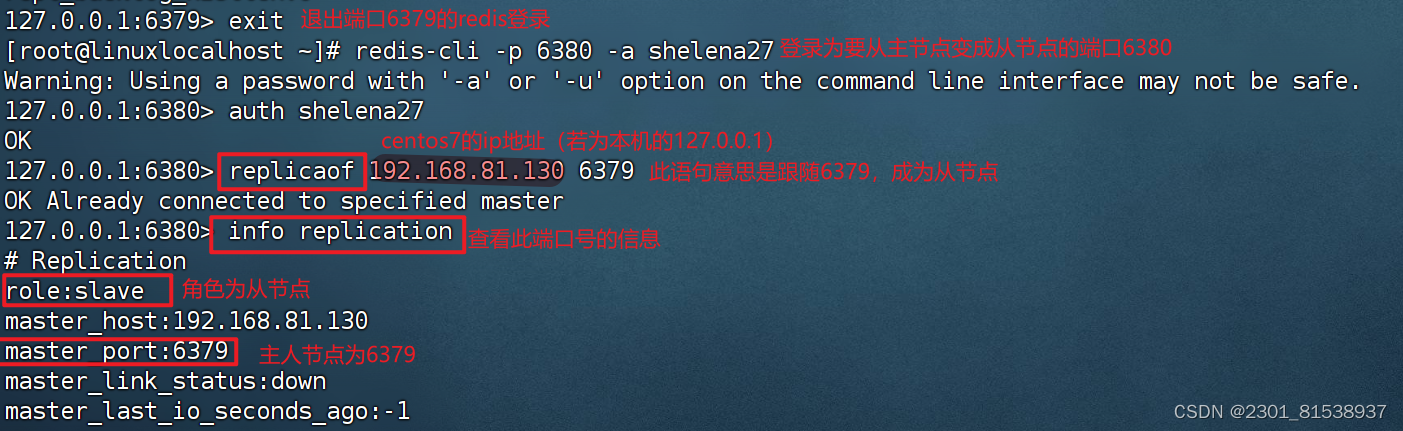
【笔记】记一次redis将从节点变成主节点 主节点变成从节点
1.连上虚拟机centos7 2.打开finalshell连接虚拟机 将从节点变为主节点 输出redis-cli -p 要变成主节点的从节点 -a此从节点的密码 输入 replicaof no one 查看端口状态 info replication 总结: redis-cli -p 端口号 -a 密码 replicaof no one info replicati…...

解析Java中1000个常用类:DoubleSummaryStatistics类,你学会了吗?
在线工具站 推荐一个程序员在线工具站:程序员常用工具(http://cxytools.com),有时间戳、JSON格式化、文本对比、HASH生成、UUID生成等常用工具,效率加倍嘎嘎好用。程序员资料站 推荐一个程序员编程资料站:程序员的成长之路(http://cxyroad.com),收录了一些列的技术教程…...

WAIC热点聚焦|新质生产力与低空经济
WAIC热点聚焦|新质生产力与低空经济 概览 # WAIC热点聚焦 | 新质生产力与低空经济## 1. 新质生产力定义与特点 - 新质生产力是在新的经济社会发展阶段中形成的,具有变革性和高增长潜力的生产能力。## 2. 低空经济概念与构成 ### 2.1 低空经济定义 - 低空经济是依托…...

Docker部署ETCD 3.5.14(保姆级图文教程)
系列文章目录 Docker部署Nginx 1.21.5(保姆级图文教程) Docker部署MySQL 8.3.0(保姆级图文教程) Docker部署ETCD 3.5.14(保姆级图文教程) 文章目录 一、环境二、拉取镜像2.1 查找 Docker Hub 上的 ETCD 镜像…...

2024年7月6日 (周六) 叶子游戏新闻
自动电脑内部录音器AutoAudioRecorder: 是一款免费的自动音频录制软件,可直接将电脑内部所有的声音录制成 mp3/wav 文件,包括音乐、游戏直播、网络会议、聊天通话等音频源。 卸载工具 HiBitUninstaller: Windows上的软件卸载工具 《不羁联盟》制作人&…...
之Requests库)
python爬虫入门(二)之Requests库
一、储备篇 1、requests库让我们可以通过python代码去构建和发送HTTP请求 2、第三方库,要先安装 python终端,输入pip install requests successfully installed:安装成功 requirement already satisfied: 说明已经安装过,无需…...

Git 操作补充:cherry-pick、变基
1. 挑选提交合并 git cherry-pick 对于多分支的代码库,将代码从一个分支转移到另一个分支是一种常见的需求,这可以分成两种情况:一种情况是,你需要另一个分支的所有代码变动,那么就采用 git merge;另一种情…...

在 PostgreSQL 中,如何处理大规模的文本数据以提高查询性能?
文章目录 一、引言二、理解 PostgreSQL 中的文本数据类型三、数据建模策略四、索引选择与优化五、查询优化技巧六、示例场景与性能对比七、分区表八、数据压缩九、定期维护十、总结 在 PostgreSQL 中处理大规模文本数据以提高查询性能 一、引言 在当今的数据驱动的世界中&…...
秋招提前批面试经验分享(下)
⭐️感谢点开文章👋,欢迎来到我的微信公众号!我是恒心😊 一位热爱技术分享的博主。如果觉得本文能帮到您,劳烦点个赞、在看支持一下哈👍! ⭐️我叫恒心,一名喜欢书写博客的研究生在读…...

零基础STM32单片机编程入门(七)定时器PWM波输出实战含源码视频
文章目录 一.概要二.PWM产生框架图三.CubeMX配置一个TIME输出1KHZ,占空比50%PWM波例程1.硬件准备2.创建工程3.测量波形结果 四.CubeMX工程源代码下载五.讲解视频链接地址六.小结 一.概要 脉冲宽度调制(PWM),是英文“Pulse Width Modulation”的缩写&…...

【ubuntu自启shell脚本】——在ubuntu中如何使用系统自带的启动应用程序设置开机自启自己的本地shell脚本
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、设置开机自启shell脚本1.使用 gnome-session-properties2.测试的shell例程代码 总结 前言 在Ubuntu系统中设置开机自启脚本是一种重要的自动化方法。开机自…...

nodejs配置国内镜像
# 设置淘宝镜像 npm config set registry https://registry.npmmirror.com# 查看镜像源 npm get registry...

【JavaEE】多线程进阶
🤡🤡🤡个人主页🤡🤡🤡 🤡🤡🤡JavaEE专栏🤡🤡🤡 文章目录 1.锁策略1.1悲观锁和乐观锁1.2重量级锁和轻量级锁1.3自旋锁和挂起等待锁1.4可…...

大模型LLM面试常见算法题-包括Attention和Transformer常见面试题
大模型: 位置编码有哪些? 介绍LoRA与QLoRA RAG和微调的区别是什么? 哪些因素会导致LLM的偏见? 什么是思维链(CoT)提示? Tokenizer的实现方法及原理 解释一下大模型的涌现能力?…...
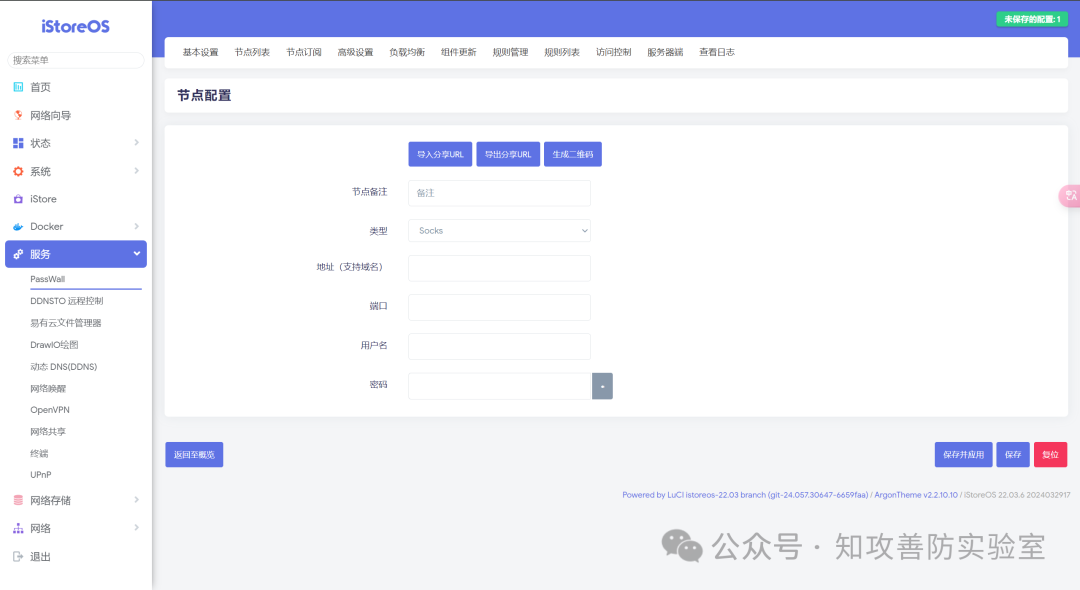
90元搭建渗透/攻防利器盒子!【硬件篇】
前言 以下内容请自行思考后进行实践。 使用场景 在某些情况下开软件进行IP代理很麻烦,并不能实现真正全局,而且还老容易忘记,那么为了在实景工作中,防止蓝队猴子封IP,此文正现。 正文 先说一下实验效果࿱…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
