AcWing 1260:二叉树输出
【题目来源】
https://www.acwing.com/problem/content/1262/
【题目描述】
树的凹入表示法主要用于树的屏幕或打印输出,其表示的基本思想是兄弟间等长,一个结点的长度要不小于其子结点的长度。
二叉树也可以这样表示,假设叶结点的长度为 1,一个非叶结点的长度等于它的左右子树的长度之和。
一棵二叉树的一个结点用一个字母表示(无重复),输出时从根结点开始:
每行输出若干个结点字符(相同字符的个数等于该结点长度),
如果该结点有左子树就递归输出左子树;
如果该结点有右子树就递归输出右子树。
假定一棵二叉树一个结点用一个字符描述,现在给出先序和中序遍历的字符串,用树的凹入表示法输出该二叉树。
【输入格式】
两行,每行是由大写字母组成的字符串(一行的每个字符都是唯一的),分别表示二叉树的先序遍历和中序遍历的序列。
【输出格式】
行数等于该树的结点数,每行的字母相同。
【数据范围】
输入字符串的长度均不超过26。
【输入样例】
ABCDEFG
CBDAFEG
【输出样例】
AAAA
BB
C
D
EE
F
G
【算法分析】
利用下图中的中序、后序遍历示意图,计算x、y值的过程,可参考确立下文代码中的参数。其中:
ile:中序遍历左端点位置,iri:中序遍历右端点位置
ple:后序遍历左端点位置,pri:后序遍历右端点位置

【算法代码】
#include <bits/stdc++.h>
using namespace std;string pre,in;
int a[30];int dfs(int l1, int r1, int l2, int r2) { //preorder & inorderif(l1==r1) {a[l1]=1;return a[l1];}int k=in.find(pre[l1]);if(k>l2) a[l1]+=dfs(l1+1,l1+k-l2,l2,k-1);if(k<r2) a[l1]+=dfs(l1+k-l2+1,r1,k+1,r2);return a[l1];
}int main() { cin>>pre>>in;dfs(0,pre.size()-1,0,in.size()-1);for(int i=0; i<pre.size(); i++) {for(int j=0; j<a[i]; j++)cout<<pre[i];cout<<endl;}return 0;
}/*
in:
ABCDEFG
CBDAFEGout:
AAAA
BB
C
D
EE
F
G
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/119108633
https://www.acwing.com/solution/content/184637/
相关文章:

AcWing 1260:二叉树输出
【题目来源】https://www.acwing.com/problem/content/1262/【题目描述】 树的凹入表示法主要用于树的屏幕或打印输出,其表示的基本思想是兄弟间等长,一个结点的长度要不小于其子结点的长度。 二叉树也可以这样表示,假设叶结点的长度为 1&…...

刷爆leetcode第十期
题目一 相同的树 给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 首先我们要来判断下它们的根是否相等 根相等的话是否它们的左子树相等 是否…...
Python28-7.5 降维算法之t-分布邻域嵌入t-SNE
t-分布邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)是一种用于数据降维和可视化的机器学习算法,尤其适用于高维数据的降维。t-SNE通过将高维数据嵌入到低维空间(通常是二维或三维)中&…...

一个最简单的comsol斜坡稳定性分析例子——详细步骤
一个最简单的comsol斜坡稳定性分析例子——详细步骤 标准模型例子—详细步骤 线弹性模型下的地应力平衡预应力与预应变、土壤塑性和安全系数求解的辅助扫描...

Java 变量类型
在Java中,变量类型包括基本数据类型和引用数据类型,每种类型有其特定的用途和存储方式。 ### 1. 基本数据类型 Java的基本数据类型包括整数类型、浮点类型、字符类型和布尔类型,它们分别是: - **整数类型**:用于存储…...
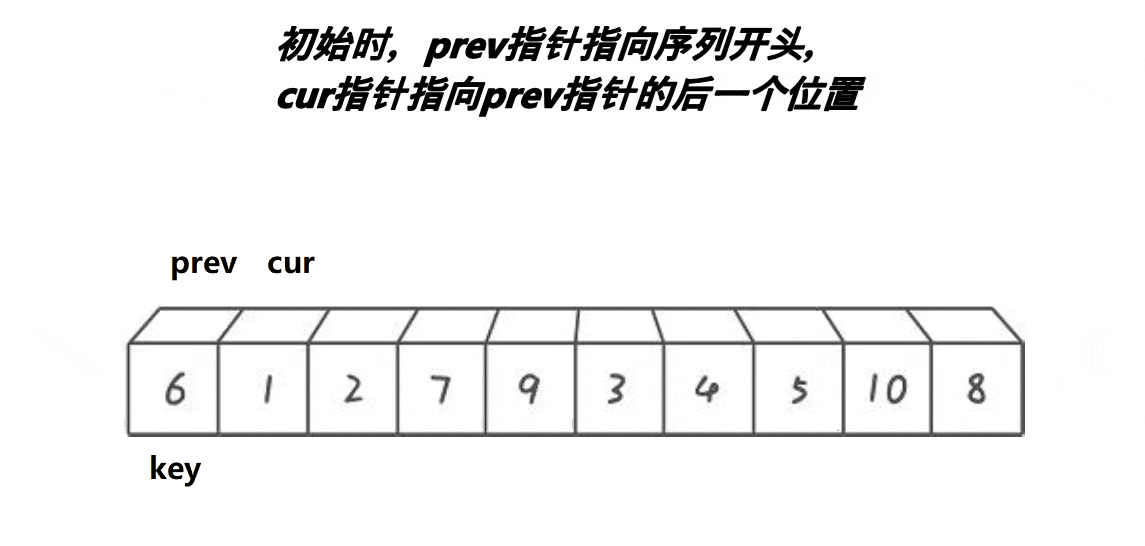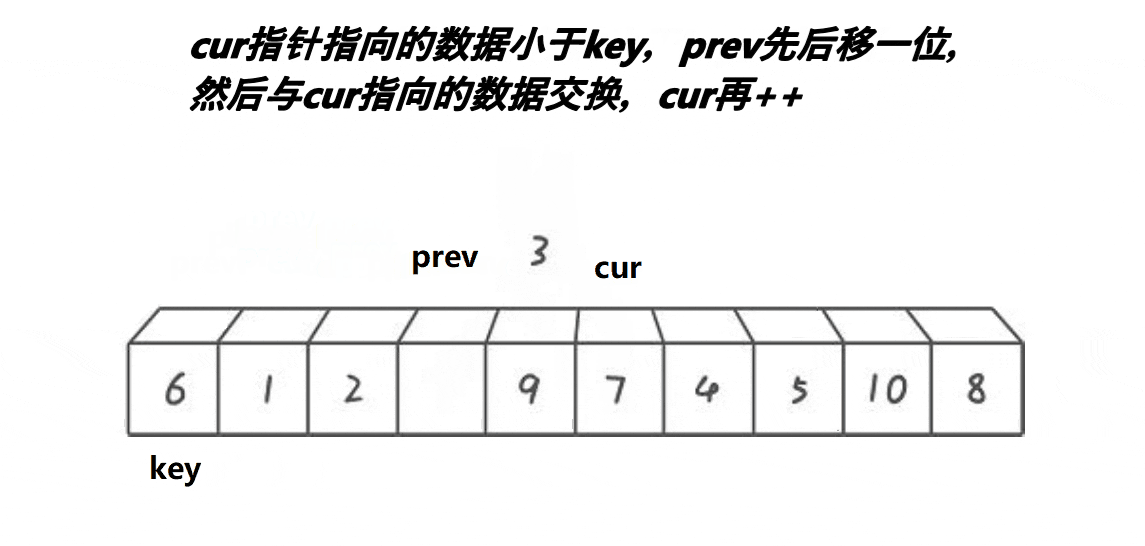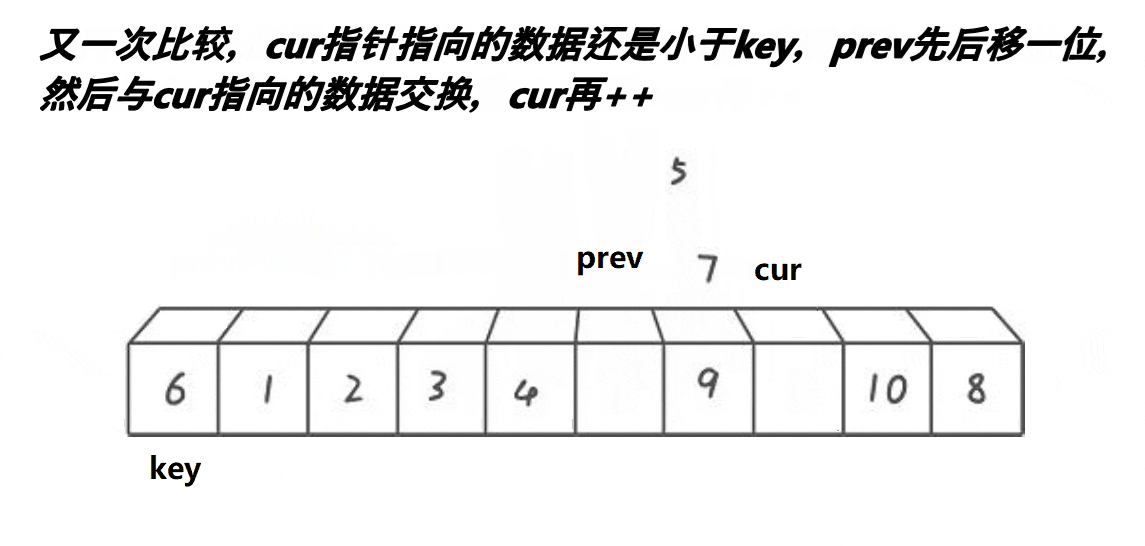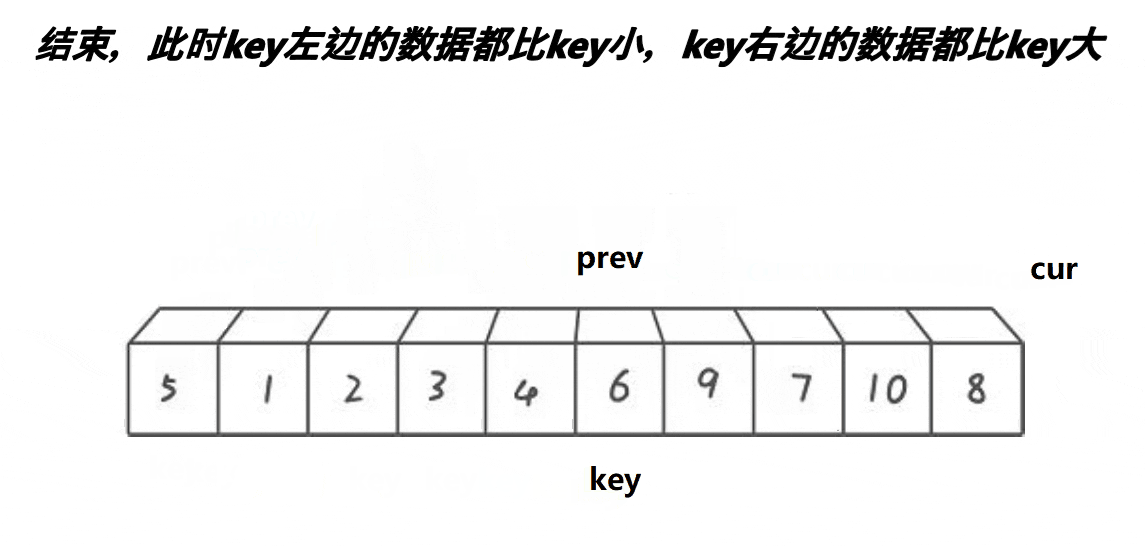
【排序算法】—— 快速排序
快速排序的原理是交换排序,其中qsort函数用的排序原理就是快速排序,它是一种效率较高的不稳定函数,时间复杂度为O(N*longN),接下来就来学习一下快速排序。 一、快速排序思路 1.整体思路 以升序排序为例: (1)、首先随…...
前端JS特效第22波:jQuery滑动手风琴内容切换特效
jQuery滑动手风琴内容切换特效,先来看看效果: 部分核心的代码如下: <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xm…...

redis的数据类型对应的使用场景
Redis提供了多种数据类型,每种数据类型都有其特定的适用场景。以下是Redis主要数据类型及其典型应用场景:1. 字符串(String) 应用场景:适用于存储简单的键值对数据,如用户基本信息、计数器(如网页访问次数&…...

ctfshow-web入门-命令执行(web118详解)Linux 内置变量与Bash切片
输入数字和小写字母,回显 evil input 查看源码,发现这里会将提交的参数 code 传给 system 函数 使用 burpsuite 抓包进行单个字符的模糊测试 fuzz: 发现过滤掉了数字和小写字母以及一些符号,下面框起来的部分是可用的 结合题目提…...

C语言 指针和数组——指针和二维数组之间的关系
目录 换个角度看二维数组 指向二维数组的行指针 按行指针访问二维数组元素 再换一个角度看二维数组 按列指针访问二维数组元素 二维数组作函数参数 指向二维数组的行指针作函数参数 指向二维数组的列指针作函数参数编辑 用const保护你传给函数的数据 小结 换个角度看…...
问题集锦1
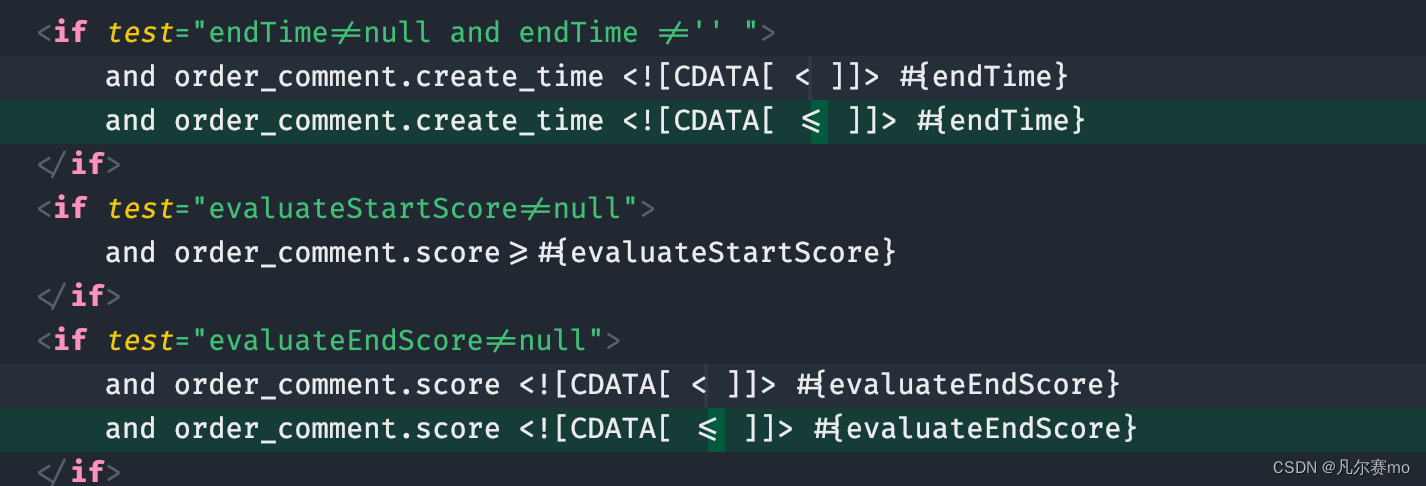
01.inner中使用JwtTokenUtil.getUserCode() 前端调用上传(java),上传使用加购 Overridepublic Boolean insertShoppingCart(InsertShoppingCartParamsDto dto) {// 通过userCode,itemCode和supplierCode来判断当前加购人添加到购物车的商品是…...

浅析MySQL-索引篇01
什么是索引? 索引是帮助存储引擎快速获取数据的一种数据结构,类似于数据的目录。 索引的分类 按数据结构分类: MySQL 常见索引有 BTree 索引、HASH 索引、Full-Text 索引。 Innodb是MySQL5.5之后的默认存储引擎,BTree索引类型也…...

2028年企业云存储支出翻倍,达到1280亿美元
根据Omdia的研究,到2028年,企业云存储支出将从去年的570亿美元翻一番以上,达到1280亿美元。该研究分析了基础设施即服务(IaaS)和平台即服务(PaaS)数据中心的收入,作为年度存储数据服…...

ActiViz中的颜色映射表vtkLookupTable
文章目录 一、简介二、VtkLookupTable的创建与初始化三、设置数据范围四、颜色映射设置五、不透明度设置六、自定义颜色映射七、 不连续性颜色映射八、 预设颜色映射方案九、可视化效果优化十、与其他VTK组件的整合十一、 动态调整映射表十二、保存和加载颜色映射表一、简介 V…...

【Spring AOP 源码解析前篇】什么是 AOP | 通知类型 | 切点表达式| AOP 如何使用
前言(关于源码航行) 在准备面试和学习的过程中,我阅读了还算多的源码,比如 JUC、Spring、MyBatis,收获了很多代码的设计思想,也对平时调用的 API 有了更深入的理解;但过多散乱的笔记给我的整理…...

Laravel HTTP客户端:网络请求的瑞士军刀
标题:Laravel HTTP客户端:网络请求的瑞士军刀 Laravel的HTTP客户端是一个功能强大的工具,它提供了一种简洁、直观的方式来发送HTTP请求。无论是与外部API集成,还是进行网络数据抓取,Laravel的HTTP客户端都能满足你的需…...

7月07日,每日信息差
第一、6 月份,北京、上海、广州和深圳的新建商品住宅成交量分别环比增加 21%、66%、48% 和 38%,均创年内新高 第二、2024 年世界人工智能大会上,上海向四家企业发放了首批无驾驶人智能网联汽车示范应用许可,这些企业可以在浦东部…...

ubuntu 网络常用命令
在Ubuntu中,有许多网络相关的常用命令。以下是一些主要命令及其用途: ifconfig:此命令用于显示和配置网络接口信息。你可以使用它来查看IP地址、子网掩码、广播地址等。 例如:ifconfig 注意:在新版本的Linux发行版中…...
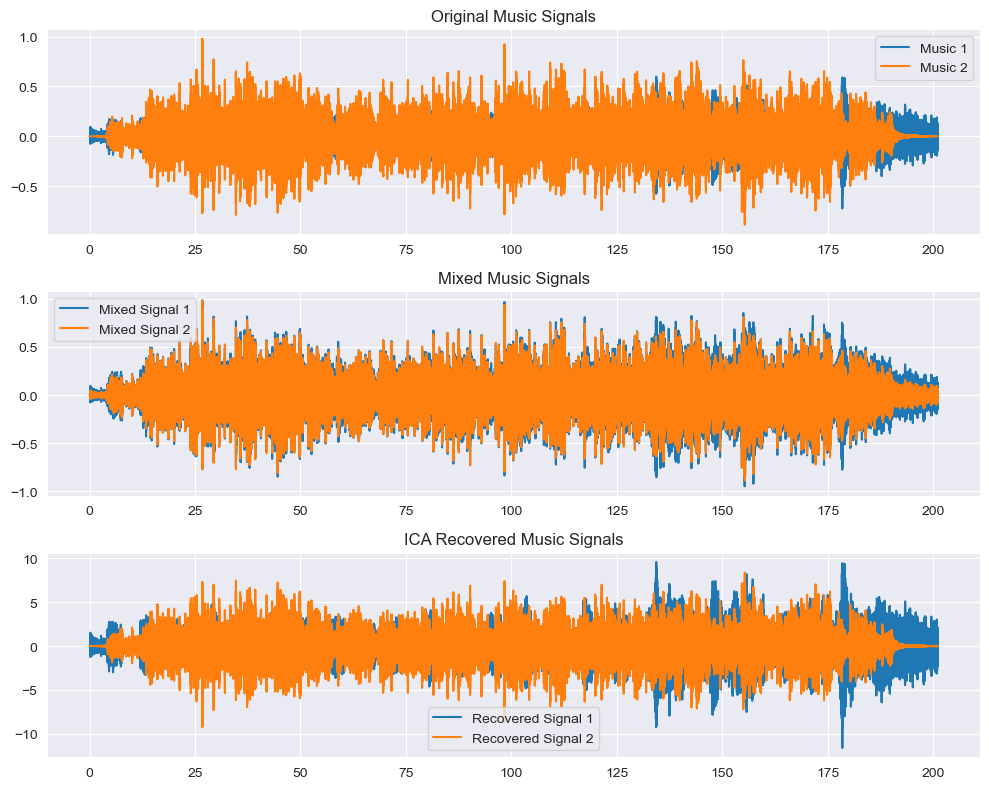
Python28-7.4 独立成分分析ICA分离混合音频
独立成分分析(Independent Component Analysis,ICA)是一种统计与计算技术,主要用于信号分离,即从多种混合信号中提取出独立的信号源。ICA在处理盲源分离(Blind Source Separation,BSS࿰…...

Spring Boot与Okta的集成
Spring Boot与Okta的集成 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中集成Okta,实现身份认证和授权的功能…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...
