cs231n 作业3
使用普通RNN进行图像标注
单个RNN神经元行为

前向传播:
反向传播:
def rnn_step_backward(dnext_h, cache):dx, dprev_h, dWx, dWh, db = None, None, None, None, Nonex, Wx, Wh, prev_h, next_h = cachedtanh = 1 - next_h**2dx = (dnext_h*dtanh).dot(Wx.T)dWx = x.T.dot(dnext_h*dtanh)dprev_h = (dnext_h*dtanh).dot(Wh.T)dWh = prev_h.T.dot(dnext_h*dtanh)db = np.sum(dnext_h*dtanh,axis=0)return dx, dprev_h, dWx, dWh, db
单层RNN神经元行为
RNN输出有两个方向,一个向上一层(输出层),一个向同层下一个时序,所以反向传播时两个梯度需要相加,输出层梯度可以直接求出(或是上一层中递归求出),所以使用dh(N,T,H)保存好,而同层时序梯度必须在同层中递归计算。

正向传播:
def rnn_forward(x, h0, Wx, Wh, b):h, cache = None, NoneN, T, D = x.shape_, H = h0.shapeh = np.zeros((N,T,H))h_next = h0cache = []for i in range(T):h[:,i,:], cache_next = rnn_step_forward(x[:,i,:], h_next, Wx, Wh, b)h_next = h[:,i,:]cache.append(cache_next)return h, cache
反向传播:
def rnn_backward(dh, cache):dx, dh0, dWx, dWh, db = None, None, None, None, Nonex, Wx, Wh, prev_h, next_h = cache[-1]_, D = x.shapeN, T, H = dh.shapedx = np.zeros((N,T,D))dh0 = np.zeros((N,H))dWx = np.zeros((D,H))dWh = np.zeros((H,H))db = np.zeros(H)dprev_h_ = np.zeros((N,H))for i in range(T-1,-1,-1):dx_, dprev_h_, dWx_, dWh_, db_ = rnn_step_backward(dh[:,i,:] + dprev_h_, cache.pop())dx[:,i,:] = dx_dh0 = dprev_h_dWx += dWx_dWh += dWh_db += db_return dx, dh0, dWx, dWh, db
使用LSTM进行图像标注
【LSTM】深入浅出讲解长短时记忆神经网络(结构、原理)
有三种方法应对梯度消失问题:
(1)合理的初始化权重值。初始化权重,使每个神经元尽可能不要取极大或极小值,以躲开梯度消失的区域。
(2)使用 ReLu 代替 sigmoid 和 tanh 作为激活函数。
(3)使用其他结构的RNNS,比如长短时记忆网络(LSTM)和 门控循环单元(GRU),这是最流行的做法。

单个LSTM神经元向前传播:
def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):next_h, next_c, cache = None, None, None_, H = prev_h.shapea = x.dot(Wx) + prev_h.dot(Wh) + bi,f,o,g = sigmoid(a[:,:H]),sigmoid(a[:,H:2*H]),sigmoid(a[:,2*H:3*H]),np.tanh(a[:,3*H:])next_c = f*prev_c + i*gnext_h = o*np.tanh(next_c)cache = [i, f, o, g, x, prev_h, prev_c, Wx, Wh, b, next_c]return next_h, next_c, cache
层LSTM神经元向前传播
def lstm_forward(x, h0, Wx, Wh, b):h, cache = None, NoneN,T,D = x.shapenext_c = np.zeros_like(h0)next_h = h0h, cache = [], []for i in range(T):next_h, next_c, cache_step = lstm_step_forward(x[:,i,:], next_h, next_c, Wx, Wh, b)h.append(next_h)cache.append(cache_step)h = np.array(h).transpose(1,0,2) #<-----------注意分析h存储后的维度是(T,N,H),需要转置为(N,T,H)return h, cache
单个LSTM神经元反向传播
def lstm_step_backward(dnext_h, dnext_c, cache):dx, dprev_h, dprev_c, dWx, dWh, db = None, None, None, None, None, Nonei, f, o, g, x, prev_h, prev_c, Wx, Wh, b, next_c = cachedo = dnext_h*np.tanh(next_c)dnext_c += dnext_h*o*(1-np.tanh(next_c)**2) #<-----------上面分析行为有提到这里的求法di, df, dg, dprev_c = (g, prev_c, i, f) * dnext_cda = np.concatenate([i*(1-i)*di, f*(1-f)*df, o*(1-o)*do, (1-g**2)*dg],axis=1)db = np.sum(da,axis=0)dx, dWx, dprev_h, dWh = (da.dot(Wx.T), x.T.dot(da), da.dot(Wh.T), prev_h.T.dot(da))return dx, dprev_h, dprev_c, dWx, dWh, db
层LSTM神经元反向传播
def lstm_backward(dh, cache):dx, dh0, dWx, dWh, db = None, None, None, None, NoneN,T,H = dh.shape_, D = cache[0][4].shapedx, dh0, dWx, dWh, db = \[], np.zeros((N, H), dtype='float32'), \np.zeros((D, 4*H), dtype='float32'), np.zeros((H, 4*H), dtype='float32'), np.zeros(4*H, dtype='float32')step_dprev_h, step_dprev_c = np.zeros((N,H)),np.zeros((N,H))for i in xrange(T-1, -1, -1):step_dx, step_dprev_h, step_dprev_c, step_dWx, step_dWh, step_db = \lstm_step_backward(dh[:,i,:] + step_dprev_h, step_dprev_c, cache[i])dx.append(step_dx) # 每一个输入节点都有自己的梯度dWx += step_dWx # 层共享参数,需要累加和dWh += step_dWh # 层共享参数,需要累加和db += step_db # 层共享参数,需要累加和dh0 = step_dprev_h # 只有最初输入的h0,即feature的投影(图像标注中),需要存储梯度dx = np.array(dx[::-1]).transpose((1,0,2))return dx, dh0, dWx, dWh, db
图像梯度:显著图和高效图像
『cs231n』作业3问题3选讲_通过代码理解图像梯度
图像生成:类别,反演和DeepDream
『cs231n』作业3问题4选讲_图像梯度应用强化
相关文章:

cs231n 作业3
使用普通RNN进行图像标注 单个RNN神经元行为 前向传播: 反向传播: def rnn_step_backward(dnext_h, cache):dx, dprev_h, dWx, dWh, db None, None, None, None, Nonex, Wx, Wh, prev_h, next_h cachedtanh 1 - next_h**2dx (dnext_h*dtanh).dot(…...
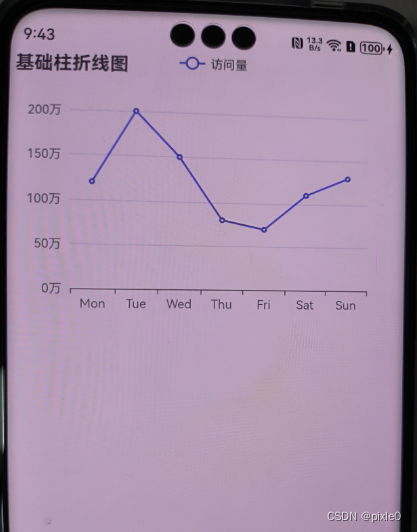
HarmonyOS Next系列之Echarts图表组件(折线图、柱状图、饼图等)实现(八)
系列文章目录 HarmonyOS Next 系列之省市区弹窗选择器实现(一) HarmonyOS Next 系列之验证码输入组件实现(二) HarmonyOS Next 系列之底部标签栏TabBar实现(三) HarmonyOS Next 系列之HTTP请求封装和Token…...

网上怎么样可以挣钱,分享几种可以让你在家赚钱的兼职项目
当今社会,压力越来越大,工作、家庭、生活等等,方方面面都需要钱,仅靠一份工作赚钱,已经很难满足我们的需求。所以很多人都会尝试做一些副业,兼职来补贴家用。 现在呢,有很多人都想在网上赚钱&am…...
)
【DevOps】运维过程中经常遇到的Http错误码问题分析(二)
目录 一、HTTP 错误400 Bad Request 1、理解 400 Bad Request 错误 2、排查 400 Bad Request 错误 3、常见的解决方法 二、HTTP 错误401 Unauthorized 1、理解 401 Unauthorized 错误 2、排查 401 Unauthorized 错误 3、常见的解决方法 一、HTTP 错误400 Bad Request …...
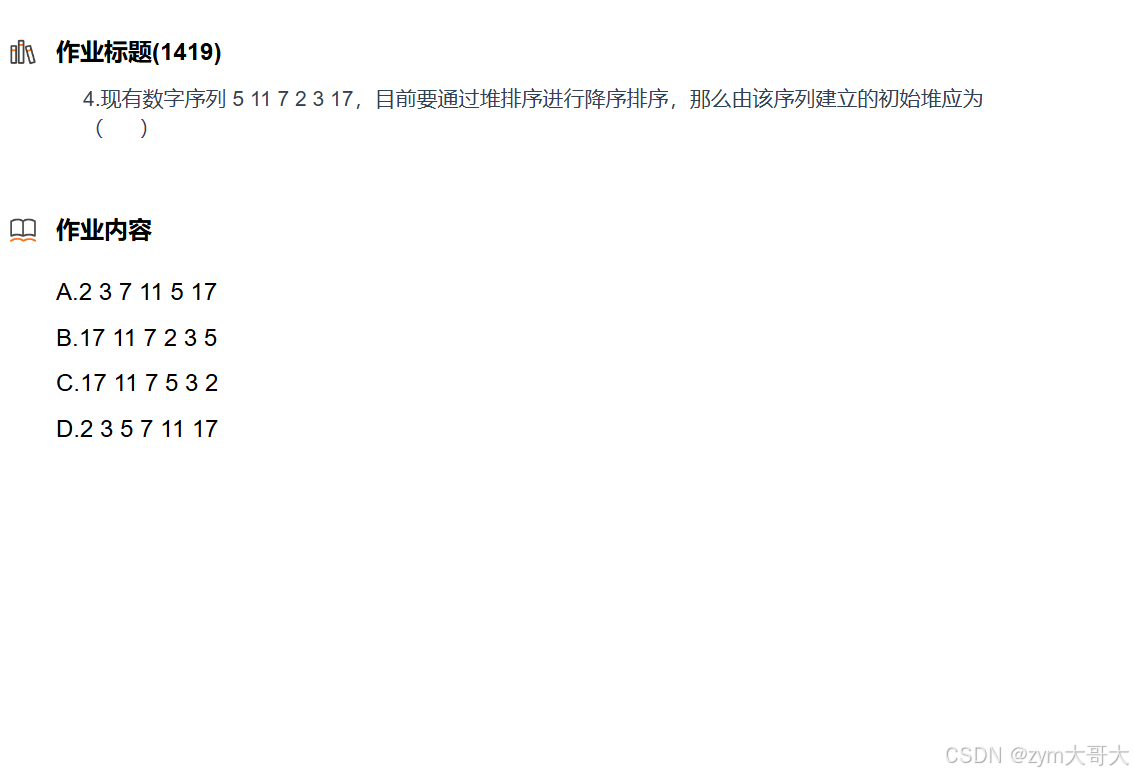
数据结构练习
1. 快速排序的非递归是通过栈来实现的,则前序与层次可以通过控制入栈的顺序来实现,因为递归是会一直开辟栈区空间,所以非递归的实现只需要一个栈的大小,而这个大小是小于递归所要的, 非递归与递归的时间复杂度是一样的…...

手动安装Ruby 1.9.3并升级RubyGems
手动安装Ruby 1.9.3并升级RubyGems ###Ruby 1.9.3 p125安装 wget http://ftp.ruby-lang.org/pub/ruby/1.9/ruby-1.9.3-p125.tar.gz \ && tar -xzvf ruby-1.9.3-p125.tar.gz \ && cd ruby-1.9.3-p125 \ && ./configure --with-openssl-dir/usr/lib/op…...

go语言day11 错误 defer(),panic(),recover()
错误: 创建错误 1)fmt包下提供的方法 fmt.Errorf(" 格式化字符串信息 " , 空接口类型对象 ) 2)errors包下提供的方法 errors.New(" 字符串信息 ") 创建自定义错误 需要实现error接口,而error接口…...

构建docker镜像实战
构建docker镜像 构建基础容器镜像(Base Image)是创建容器化应用程序的第一步。基础镜像提供了一个最低限度的操作系统环境,您可以在其上安装所需的软件包和应用程序。 Dockerfile语法说明 Dockerfile 是 Docker 构建镜像的描述文件&#x…...

生信算法9 - 正则表达式匹配氨基酸序列、核型和字符串
建议在Jupyter实践。 1. 使用正则表达式匹配指定的氨基酸序列 import re# 氨基酸序列 seq VSVLTMFRYAGWLDRLYMLVGTQLAAIIHGVALPLMMLI# 正则表达式匹配 match re.search(r[A|G]W, seq)# 打印match及匹配到开始位置和结束位置 print(match) # <re.Match object; span(10, …...

linux ext2文件系统浅析
文章目录 前言ext2内容概述实验准备二进制对比分析1 super block2 group desc3 block bitmap4 inode bitmap5 inode_tableinode 1inode 2inode 11inode 12 6 dir entry7 data区8 间接块9 块组 前言 网上关于ext2文件系统的博客有很多,但看完之后还是有些云里雾里&a…...

「树莓派入门」树莓派进阶02-传感器应用与交通灯项目
传感器是树莓派实现智能化的关键。通过本教程,你可以开始尝试使用传感器来增强树莓派的功能。 一、传感器在树莓派中的作用 传感器是树莓派与外界环境交互的重要工具。它们可以检测各种物理量,如光、声音、温度等,并将这些物理量转换为电信号,供树莓派读取和处理。 二、数…...

pytorch 指定GPU设备
使用os.environ["CUDA_VISIBLE_DEVICES"] 这种方法是通过环境变量限制可见的CUDA设备,从而在多个GPU的机器上只让PyTorch看到并使用指定的GPU。这种方式的好处是所有后续的CUDA调用都会使用这个GPU,并且代码中不需要显式地指定设备索引。 im…...

华为od-C卷200分题目6 - 5G 网络建设
华为od-C卷200分题目6 - 5G 网络建设 题目描述 现需要在某城市进行 5G 网络建设,已经选取 N 个地点设置 5G 基站,编号固定为 1 到 N,接下来需要各个基站之间使用光纤进行连接以确保基站能互联互通,不同基站之间架设光纤的成本各不…...
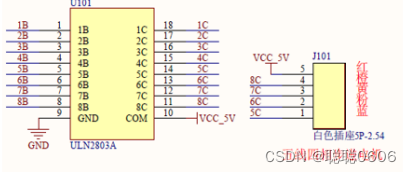
步进电机(STM32+28BYJ-48)
一、简介 步进电动机(stepping motor)把电脉冲信号变换成角位移以控制转子转动的执行机构。在自动控制装置中作为执行器。每输入一个脉冲信号,步进电动机前进一步,故又称脉冲电动机。步进电动机多用于数字式计算机的外部设备&…...

Node.js介绍 , 安装与使用
1.Node.js 1 什么是Node.js 官网:https://nodejs.org/zh-cn/ 中文学习网:http://nodejs.cn/learn1.Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。Node.js 使用了一个事件驱动、非阻塞式 I/O 的模型,使其轻量又高效。 2.前端的底层 html…...
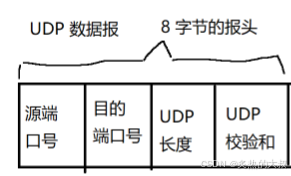
JavaEE初阶-网络原理1
文章目录 前言一、UDP报头二、UDP校验和2.1 CRC2.2 md5 前言 学习一个网络协议,最主要就是学习的报文格式,对于UDP来说,应用层数据到达UDP之后,会给应用层数据报前面加上UDP报头。 UDP数据报UDP包头载荷 一、UDP报头 如上图UDP的…...
)
leetcode秋招冲刺 (专题16--18)
专题16:分治 题目169:多数元素(YES) 解题思路:使用哈希表可以统计出现次数的性质,直接统计就行。 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊…...

学懂C#编程:实用方法——string字符串指定连接符拼接之 string.Join 的详细用法
在C#中,string.Join 方法用于将一个字符串数组或集合中的元素连接成一个单一的字符串,并在每个元素之间插入指定的分隔符。这个方法非常有用,特别是在需要将多个字符串合并成一个字符串时。以下是 string.Join 方法的详细用法: 方…...
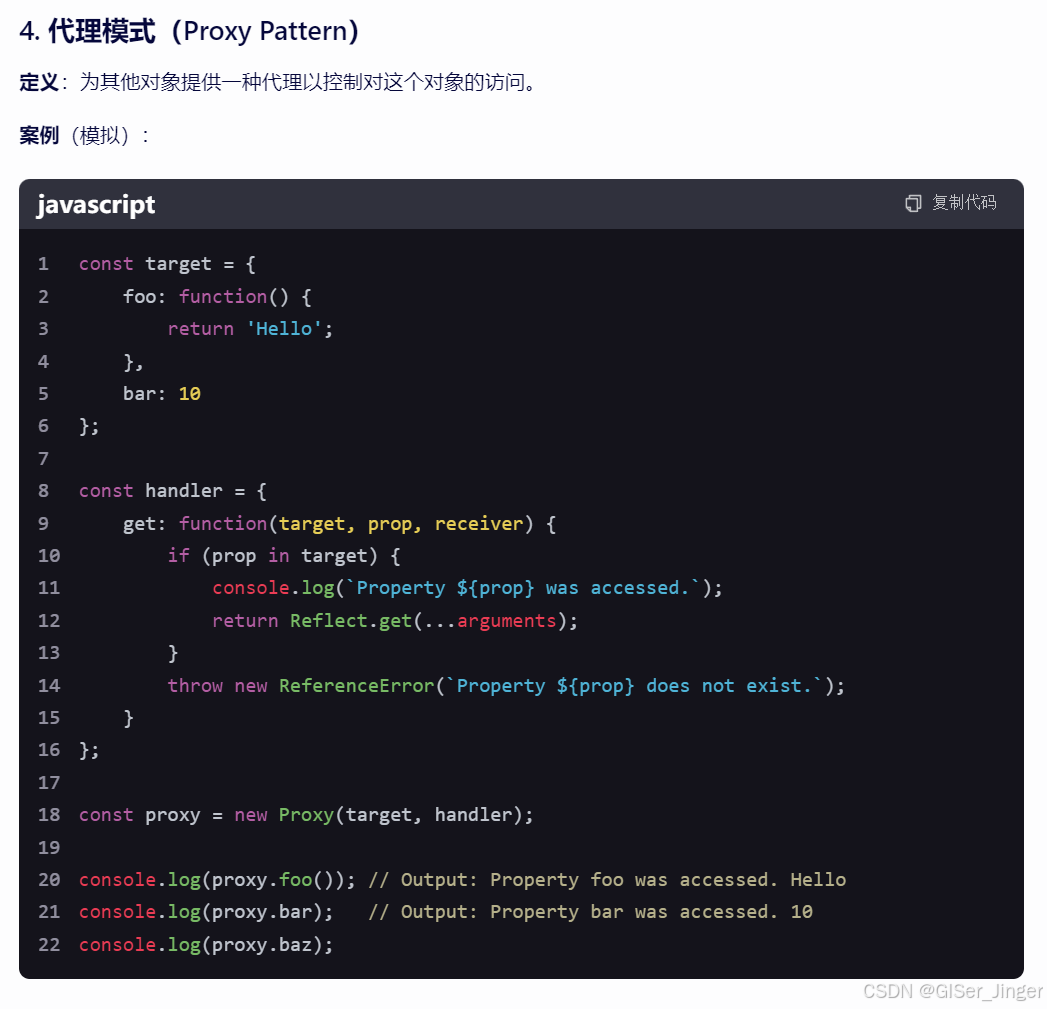
Javascript常见数据结构和设计模式
在JavaScript中,常见的数据结构包括两大类:原始数据类型(Primitive Types)和对象类型(Object Types)。对象类型又可以进一步细分为多种内置对象、数组、函数等。下面是一些JavaScript中常见的数据结构&…...

【ChatGPT】全面解析 ChatGPT:从起源到未来
ChatGPT 是由 OpenAI 开发的一个基于 GPT(Generative Pre-training Transformer)架构的聊天机器人。通过自然语言处理(NLP)技术,ChatGPT 能够理解和生成语言,与人类进行对话。本文将深入探讨其起源、发展、…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
