华为od-C卷200分题目6 - 5G 网络建设
华为od-C卷200分题目6 - 5G 网络建设
题目描述
现需要在某城市进行 5G 网络建设,已经选取 N 个地点设置 5G 基站,编号固定为 1 到 N,接下来需要各个基站之间使用光纤进行连接以确保基站能互联互通,不同基站之间架设光纤的成本各不相同,且有些节点之间已经存在光纤相连,请你设计算法,计算出能联通这些基站的最小成本是多少。
注意,基站的联通具有传递性,即基站 A 与基站 B 架设了光纤基站 B 与基站 C 也架设了光纤,则基站 A 与基站 C 视为可以互相联通
输入
第一行输入表示基站的个数 N,其中 0 < N <= 20
第二行输入表示具备光纤直连条件的基站对的数目 M,其中 0 < M < N * (N - 1) / 2
第三行开始连续输入 M 行数据,格式为 X Y Z P,其中 X Y 表示基站的编号,0 < X <= N, 0 < Y <= N 且 X 不等于 Y, Z 表示在 X Y 之间架设光纤的成本,其中 0 < Z < 100,P 表示是否已存在光纤连接,0 表示未连接, 1 表示已连接。
输出
如果给定条件,可以建设成功互联互通的 5G 网络,则输出最小的建设成本,
如果给定条件,无法建设成功互联互通的 5G 网络,则输出-1
样例输入 复制
3
3
1 2 3 0
1 3 1 0
2 3 5 0
样例输出 复制
4
提示
只需要在 1,2 以及 2,3 基站之间铺设光纤,其成本为 3+1=4
import java.util.*;class Point {int parent;int size = 1;int cost = 0;public Point(int parent) {this.parent = parent;}
}public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int m = sc.nextInt();int x, y, z, p;Point[] points = new Point[n + 1];for (int i = 1; i < points.length; i++) {points[i] = new Point(i);}ArrayList<int[]> list = new ArrayList<>();HashSet<Integer> set = new HashSet<>();for (int i = 0; i < m; i++) {x = sc.nextInt();y = sc.nextInt();z = sc.nextInt();p = sc.nextInt();set.add(x);set.add(y);if (p == 1) {add(points, x, y, 0);} else {list.add(new int[]{x, y, z});}}Collections.sort(list, Comparator.comparingInt(o -> o[2]));for (int[] ints : list) {add(points, ints[0], ints[1], ints[2]);}int parent = -1;for (int i = 1; i <= n; i++) {if (parent == -1) {parent = getParent(points, i);}if (parent != getParent(points, i)) {System.out.println(-1);return;}}System.out.println(points[parent].cost);}private static void add(Point[] points, int x, int y, int cost) {int parentX = getParent(points, x);int parentY = getParent(points, y);if (parentY == parentX) {return;}if (points[parentY].size <= points[parentX].size) {points[parentY].parent = points[parentX].parent;points[parentX].size += points[parentY].size;points[parentX].cost += cost + points[parentY].cost;} else {points[parentX].parent = points[parentY].parent;points[parentY].size += points[parentX].size;points[parentY].cost += cost + points[parentX].cost;}}public static int getParent(Point[] points, int index) {while (index != points[index].parent) {index = points[index].parent;}return index;}
}思路:主要就是并查集的思想,不断更新父节点,比较时比较size,哪个集合多哪个就作为父,先排序,按照成本排序,如果已经连接则跳过
相关文章:

华为od-C卷200分题目6 - 5G 网络建设
华为od-C卷200分题目6 - 5G 网络建设 题目描述 现需要在某城市进行 5G 网络建设,已经选取 N 个地点设置 5G 基站,编号固定为 1 到 N,接下来需要各个基站之间使用光纤进行连接以确保基站能互联互通,不同基站之间架设光纤的成本各不…...
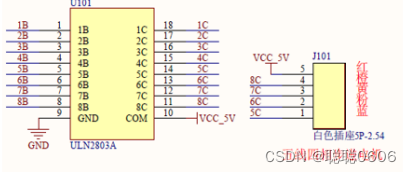
步进电机(STM32+28BYJ-48)
一、简介 步进电动机(stepping motor)把电脉冲信号变换成角位移以控制转子转动的执行机构。在自动控制装置中作为执行器。每输入一个脉冲信号,步进电动机前进一步,故又称脉冲电动机。步进电动机多用于数字式计算机的外部设备&…...

Node.js介绍 , 安装与使用
1.Node.js 1 什么是Node.js 官网:https://nodejs.org/zh-cn/ 中文学习网:http://nodejs.cn/learn1.Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。Node.js 使用了一个事件驱动、非阻塞式 I/O 的模型,使其轻量又高效。 2.前端的底层 html…...
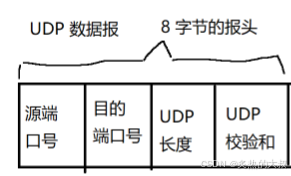
JavaEE初阶-网络原理1
文章目录 前言一、UDP报头二、UDP校验和2.1 CRC2.2 md5 前言 学习一个网络协议,最主要就是学习的报文格式,对于UDP来说,应用层数据到达UDP之后,会给应用层数据报前面加上UDP报头。 UDP数据报UDP包头载荷 一、UDP报头 如上图UDP的…...
)
leetcode秋招冲刺 (专题16--18)
专题16:分治 题目169:多数元素(YES) 解题思路:使用哈希表可以统计出现次数的性质,直接统计就行。 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊…...

学懂C#编程:实用方法——string字符串指定连接符拼接之 string.Join 的详细用法
在C#中,string.Join 方法用于将一个字符串数组或集合中的元素连接成一个单一的字符串,并在每个元素之间插入指定的分隔符。这个方法非常有用,特别是在需要将多个字符串合并成一个字符串时。以下是 string.Join 方法的详细用法: 方…...
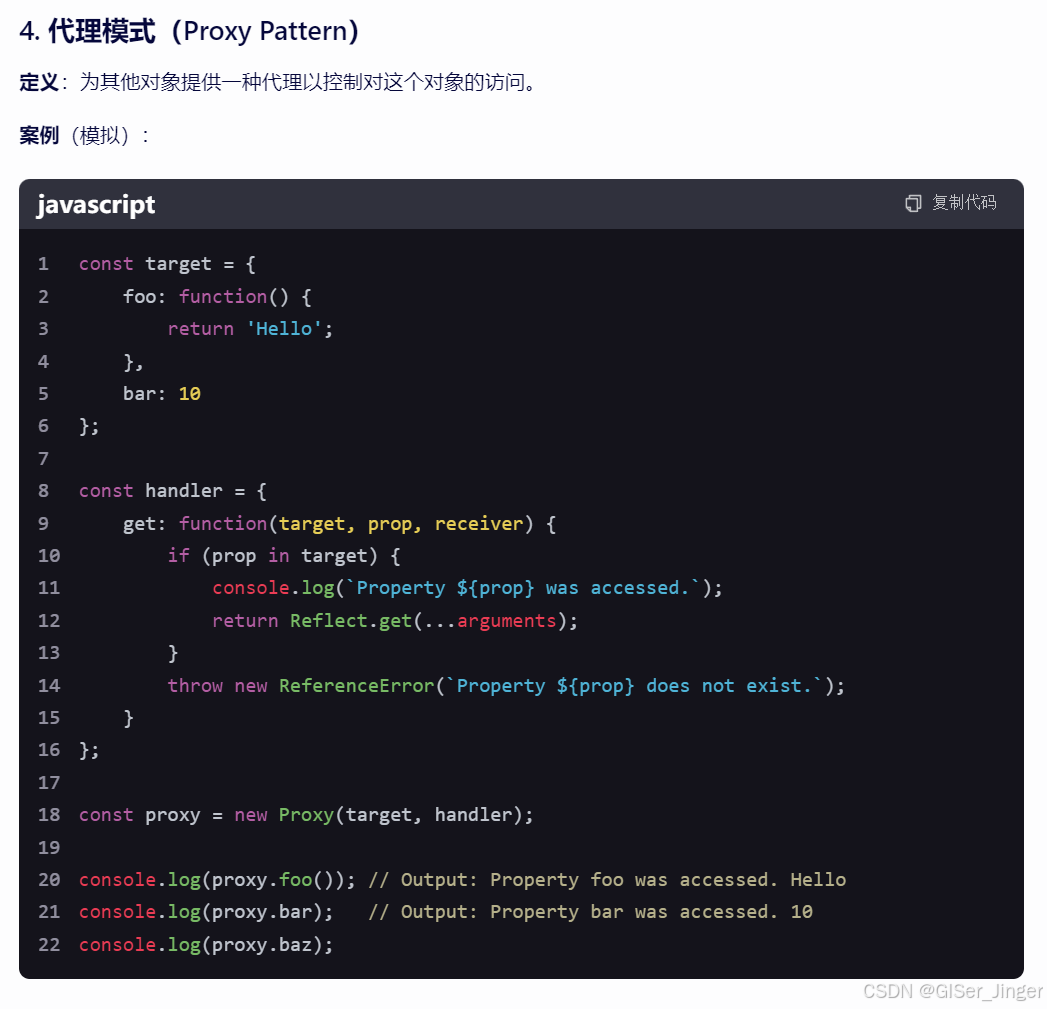
Javascript常见数据结构和设计模式
在JavaScript中,常见的数据结构包括两大类:原始数据类型(Primitive Types)和对象类型(Object Types)。对象类型又可以进一步细分为多种内置对象、数组、函数等。下面是一些JavaScript中常见的数据结构&…...

【ChatGPT】全面解析 ChatGPT:从起源到未来
ChatGPT 是由 OpenAI 开发的一个基于 GPT(Generative Pre-training Transformer)架构的聊天机器人。通过自然语言处理(NLP)技术,ChatGPT 能够理解和生成语言,与人类进行对话。本文将深入探讨其起源、发展、…...
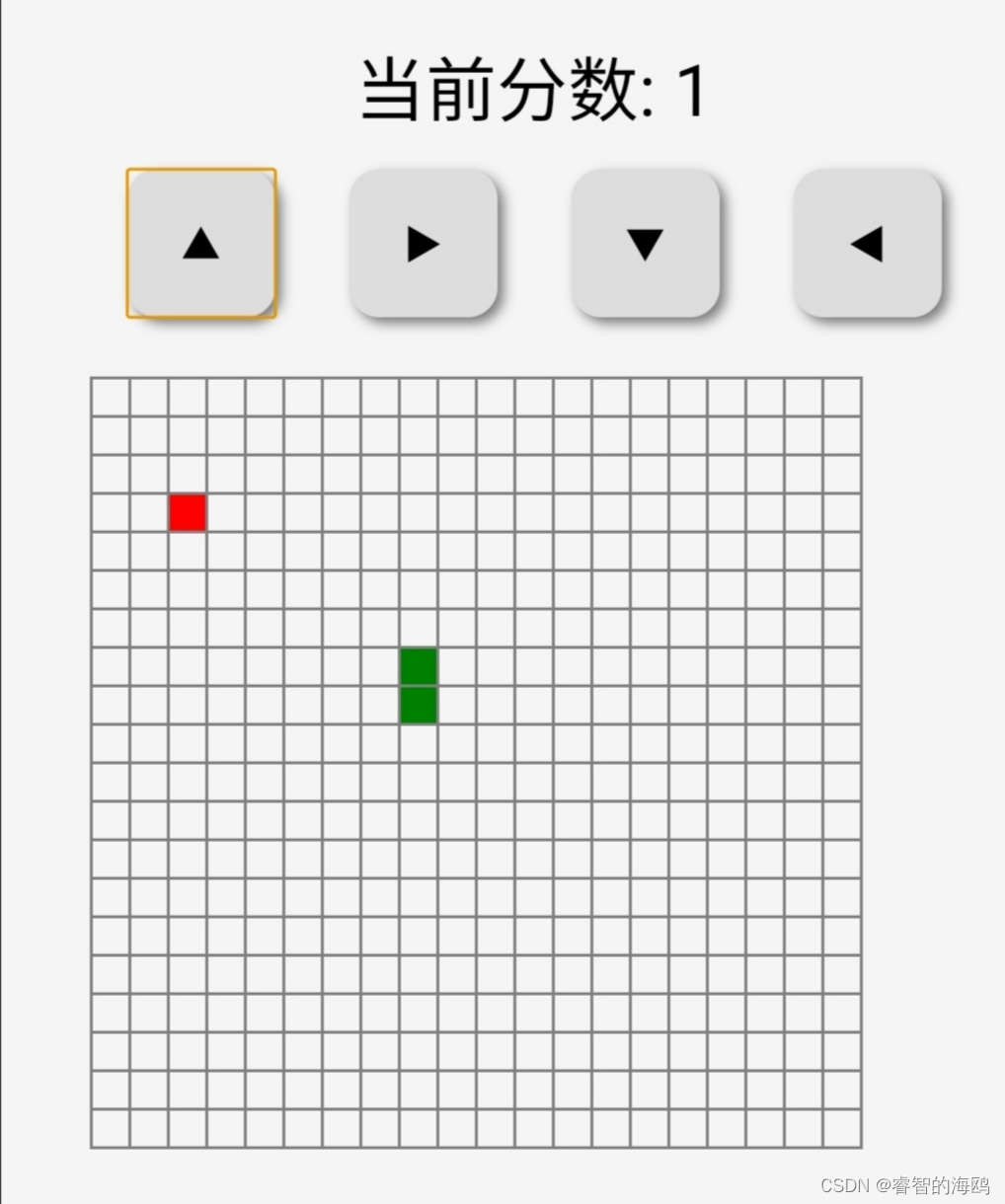
html+css+js贪吃蛇游戏
贪吃蛇游戏🕹四个按钮控制方向🎮 源代码在图片后面 点赞❤️关注🙏收藏⭐️ 互粉必回🙏🙏😍😍😍 源代码📟 <!DOCTYPE html> <html lang"en"&…...
新手必学:掌握Excel中这些常用公式,轻松提升数据处理能力
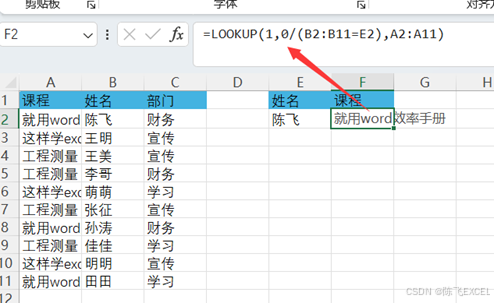
各位同学好,今天和大家来分享几个常用函数公式的典型用法。 1、提取指定条件的不重复名单 如下图所示,某公司课程比赛,同一员工有多个比赛项目。希望从左侧的列表中,提取出财务部的参赛人员名单。F2单元格输入以下公式࿰…...
经济寒冬:竞品凶猛,你的产品如何求生?
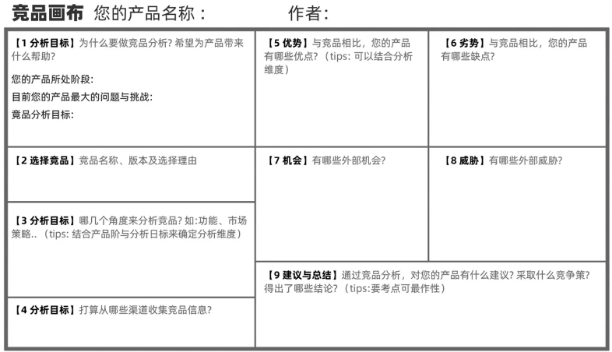
那些年曾被竞品干掉的产品 1997年到2010年左右是国内互联网行业的快速发展和多元化发展的时期,这一时期涌现出来一大批优秀的产品,市场竞争越来越激烈。苹果 在20 世纪 80 年代,乔布斯的苹果电脑,在当时可是PC行业的老大…...

信号量——Linux并发之魂
欢迎来到 破晓的历程的 博客 引言 今天,我们继续学习Linux线程本分,在Linux条件变量中,我们对条件变量的做了详细的说明,今天我们要利用条件变量来引出我们的另一个话题——信号量内容的学习。 1.复习条件变量 在上一期博客中&…...
详解)
自动驾驶中的逆透视变换(Inverse Perspective Mapping,IPM)详解
前言 IPM(Inverse Perspective Mapping,逆透视变换)图的历史可以追溯到计算机视觉和图像处理领域的发展。逆透视变换是一种用于消除图像中透视效应的技术,使得原本由于透视产生的形变得以纠正,进而更准确地描述和理解图像中的场景。比如在行车中的车道线检测,泊车中的常见…...

Python地震波逆问题解构算法复杂信号分析
🎯要点 🎯时域、时频域以及时间和频率相关联偏振特性分析三种算法 | 🎯时域波参数估计算法 | 🎯机器学习模型波形指纹分析算法 | 🎯色散曲线和频率相关波分析算法 | 🎯动态倾斜校正算法 | 🎯声…...
C语言 -- 深入理解指针(二)
C语言 -- 深入理解指针(二) 1. 数组名的理解2. 使用指针访问数组3. 一维数组传参的本质4. 冒泡排序5. 二级指针6. 指针数组7. 指针数组模拟二维数组8. 字符指针变量9. 数组指针变量2.1数组指针变量是什么?2.2 数组指针变量怎么初始化 10. 二维…...

HTTP协议详解
HTTP协议详解 一、HTTP协议概述二、网络基础与HTTP2.1 TCP/IP协议2.2 发送HTTP请求过程2.3 HTTP请求的组成部分 三、HTTP报文HTTP请求报文HTTP响应报文 结语 一、HTTP协议概述 HTTP,即超文本传输协议(Hypertext Transfer Protocol)ÿ…...

一年时间业绩增长2倍,茅台保健酒业公司在川销售的“三板斧”
执笔 | 尼 奥 编辑 | 扬 灵 作为土地面积全国第5、人口总数全国第3、GDP全国第6的产酒、销酒大省,四川酒类消费总额已达800亿元,其中白酒市场规模达到500亿元。 近年来,随着省外名酒提升对四川市场重视,其市场份额也从20年前的3%…...

土豆炒肉做法
菜单:土豆、葱、铁辣子、纯瘦肉、淀粉、生抽、酱油、刀、案板、十三香、盐巴、擦板 流程: 洗土豆,削皮,擦成条,用凉水过滤两遍淀粉,顺便放个燥里洗肉,切成条,按照生抽、酱油、淀粉、…...

VPS拨号服务器:独享的高效与安全
在当今互联网高速发展的时代,虚拟私人服务器(VPS)已成为许多企业和个人用户托管网站、应用程序的首选。特别是带有拨号功能的VPS服务器,以其独特的优势受到广泛关注。本文将深入探讨VPS拨号服务器的独享特性,以及它如何…...

网络安全设备——防火墙
网络安全设备防火墙是一种用来加强网络之间访问控制的特殊网络互联设备。以下是对防火墙的详细解释: 一、定义与基本概念 定义:防火墙是指设置在不同网络(如可信任的企业内部网和不可信的公共网)或网络安全域之间的一系列部件的…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...
