【DFS(深度优先搜索)详解】看这一篇就够啦
【DFS详解】看这一篇就够啦
- 🍃1. 算法思想
- 🍃2. 三种枚举方式
- 🍃2.1 指数型枚举
- 🍃2.2 排列型枚举
- 🍃2.3 组合型枚举
- 🍃3. 剪枝优化
- 🍃4. 图的搜索
- 🍃5. 来几道题试试手
- 🍃5.1 选数
- 🍃5.2 火柴棒等式
🚀欢迎互三👉: 2的n次方_💎💎
🚀所属专栏:数据结构与算法学习⭐⭐

🍃1. 算法思想
DFS算法的基本思想是从图中的某个顶点v出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,整个进程反复进行直到所有顶点都被访问为止。

从上图中可以直观的感受到这种思想
就是一条路走到黑的思想,走到无路可走再回退到上一层,再选择另一条路继续一直走,再回退,直到整个遍历完成,深度优先搜索一般是通过递归来实现的,“递”的过程就是往下搜的过程对应着深度,“归”的过程就是回溯,回退上一级
🍃2. 三种枚举方式
🍃2.1 指数型枚举
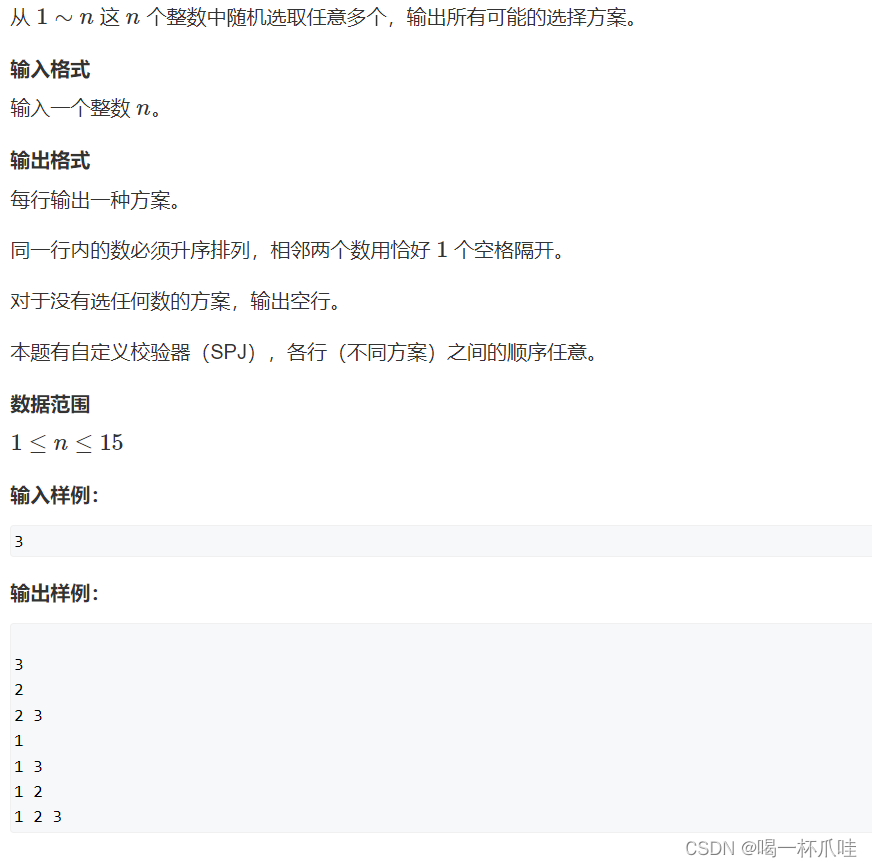
指数型枚举是指一共有n个数,每一个数都有两种状态,也就是选或不选,时间复杂度也就是2^n,指数级的
例如3个数的枚举时,每一个数都有选和不选两种状态,可以根据这个画出递归搜索树

接着用代码实现一下
#include <iostream>
using namespace std;
int n;
int vis[20];
void dfs(int x){//表示已经n个数都被判断过了,一种方案已经搜索完成if(x > n){for(int i = 1;i <= n;i++){if(vis[i] == 1)cout<<i<<" ";}cout<<'\n';return;}vis[x] = 2;//表示不选dfs(x+1);//继续搜下一个vis[x] = 0;//回溯vis[x] = 1;//表示选dfs(x+1);//继续搜下一个vis[x] = 0;//回溯}
int main(){cin>>n;dfs(1);return 0;
}
🍃2.2 排列型枚举
排列型枚举是一种生成给定集合所有可能排列的方法,其实在中学阶段我们就学过排列组合的问题,排列是区分顺序的,例如,同样是1 2 3三个数字,1,2, 3和 1,3,2是两种方案。
来看下面的一个例题:
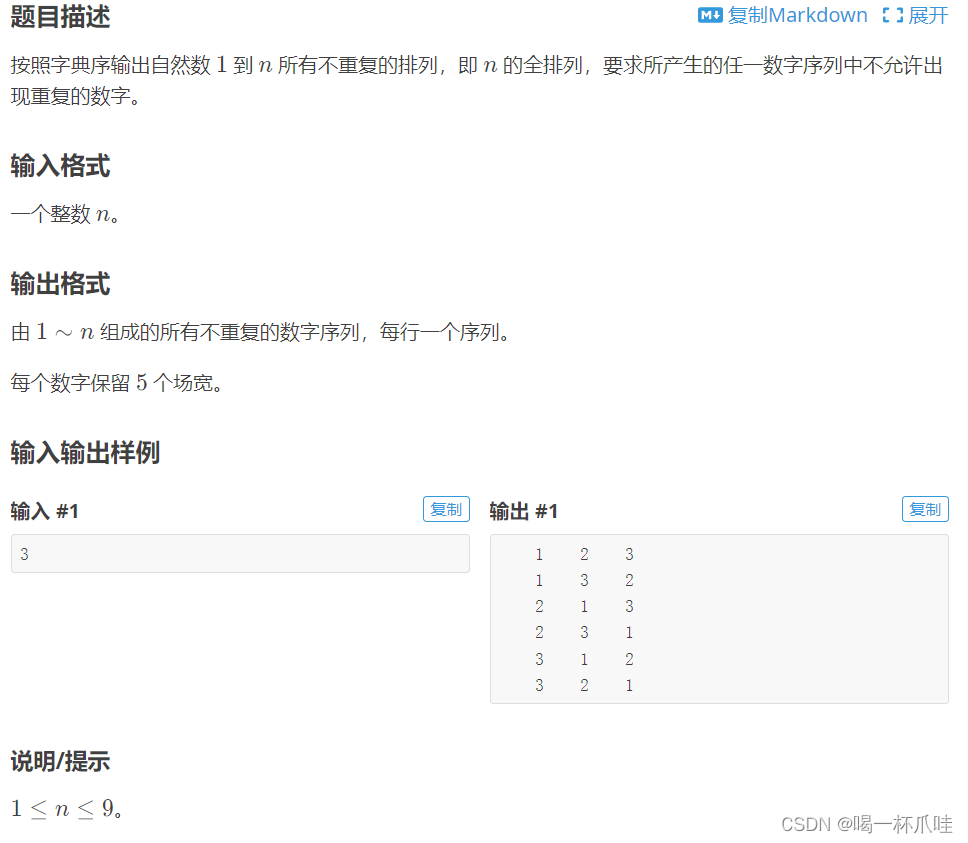
很简单,就是生成n个数字的全排列方案,在用代码实现的过程中,需要另外再开一个vis数组,表示状态,以此来区分是否被选过
#include <bits/stdc++.h>
using namespace std;
int vis[15];
int a[15];
int n;
void dfs(int x){//表示n个数字都已经选过了if(x > n){for(int i = 1;i <= n;i++){cout<<setw(5)<<a[i];//题目中要求5个场宽}cout<<'\n';return;}for(int i = 1;i <= n;i++){if(!vis[i]){vis[i] = 1;//选过标记为1a[x] = i;//表示该数字被选上了dfs(x+1);//继续选下一个数字vis[i] = 0;//回溯重置该数字的状态a[x] = 0;//,也可以不写,因为数据可以直接覆盖}}
}int main(){cin>>n;dfs(1);return 0;
}
也就是依次枚举n个数,当这n个数选出一种方案之后,就回溯,再判断其它分支
🍃2.3 组合型枚举
组合是从n个不同元素中取出m(m≤n)个元素的所有取法,组合不考虑元素的顺序。也就是 1 2 3 和 1 3 2是同一种方案
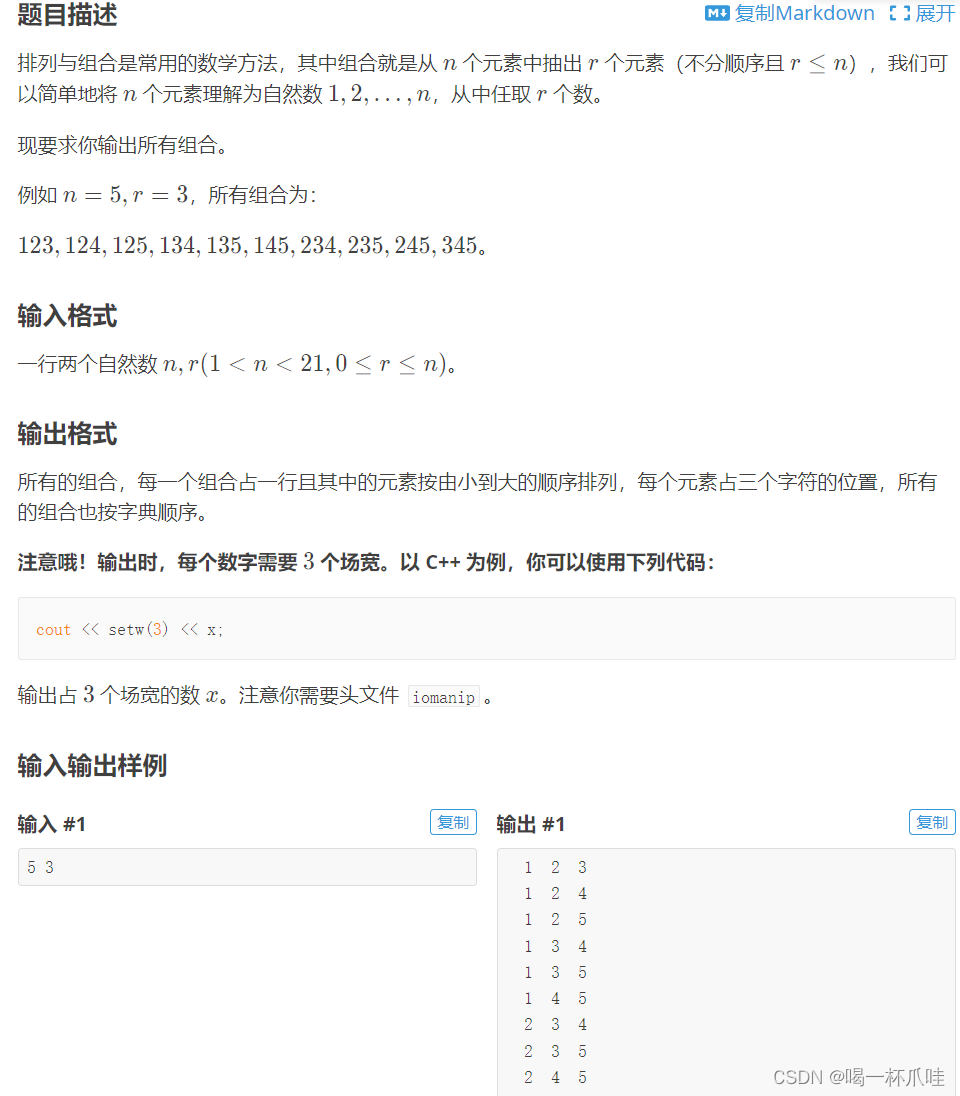
这次的dfs中采用了两个参数,一个表示枚举了几个数,一个表示从哪个数开始往后选,因为这次是组合型枚举,例如,在选了1 3 2之前,1 2 3肯定也已经选过了,所以不会有1 3 2这种情况出现,从哪个数开始往后选,都是选的比这个数字典序大的数,不存在字典数大的数排在字典数小的之前的情况,所以要记录从哪个数开始往后选
#include <bits/stdc++.h>
using namespace std;
int a[25];
int n,r;
void dfs(int x,int start){//已经选够的情况if(x > r){for(int i = 1;i<=r;i++){cout<<setw(3)<<a[i];}cout<<'\n';return;}for(int i = start;i<=n;i++){a[x] = i;dfs(x+1,i+1);//选下一个数字,并且下一个数字的字典序要比本次大,也就是从i+1开始往后选a[x] = 0;}
}
int main(){cin>>n>>r;dfs(1,1);return 0;
}
🍃3. 剪枝优化
在深度优先搜索(DFS)中,剪枝是一种常用的优化技术,用于减少不必要的搜索空间,从而提高搜索效率。剪枝的核心思想是在搜索过程中,尽早地识别和排除那些不可能产生解的路径或状态,从而避免在这些无效路径上浪费时间和资源。
dfs(深度优先搜索)其实是一种特别暴力的算法,也就是我们常说的暴力搜索,时间复杂度一般都是指数级或阶乘级的这样,这时,剪枝就显得尤为重要,不然特别容易超时

来看一道洛谷的典型题:P1088:火星人

这题是不是就是我们之前讲到的全排列类型的题,意思就是给出一个排列方式,按照字典序求这种方式以后的第几种排列
这次用Java实现一下:
public class Main {static int n = 0, r = 0;//n个数字,求第r中排列方式static int cnt = 0;//记录次数static int[] arr = new int[10010];static int[] mars = new int[10010];//火星人的排列static boolean[] vis = new boolean[10010];//记录状态static boolean falg = false;//记录状态,后面用于剪枝public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();r = sc.nextInt();for (int i = 1; i <= n; i++) {mars[i] = sc.nextInt();}dfs(1);}public static void dfs(int x) {//剪枝,后面的不用再去排列了if (falg) {return;}if (x > n) {cnt++;if (cnt == r + 1) {//表示已经找到了答案falg = true;for (int i = 1; i <= n; i++) {System.out.print(arr[i] + " ");}System.out.println();}return;}//和之前写的排列模板一样for (int i = 1; i <= n; i++) {//表示从火星人给出的排列方案开始往后搜索if (cnt == 0) {i = mars[x];}if (!vis[i]) {arr[x] = i;vis[i] = true;dfs(x + 1);vis[i] = false;}}}
}
这道题我们就很好的利用了剪枝进行优化,不然按照原来算法的时间复杂度肯定是会超时的,当我们找到目标方案之后,后面的方案就没必要进行搜索了,此时直接退出函数,也就是剪枝
每一题的剪枝方案需要具体题目具体分析。
🍃4. 图的搜索
步骤:
1.选择起始点:从图的某个顶点v开始。
2.标记当前顶点:将当前顶点v标记为已访问,以避免重复访问。
3.遍历邻接点:对于v的每个未访问的邻接点w,递归地执行DFS,从w开始。
4.回溯:当没有更多的邻接点可以遍历时,返回到上一步的顶点。
下面看一道例题:
洛谷1683:入门
图的存储:通过二维数组进行存储
怎么往四个方向进行搜索:定义两个方向数组

#include <iostream>
using namespace std;
const int N = 25;
char arr[N][N];
bool vis[N][N];
int res;
int x, y;
//方向数组,四个方向进行搜索
int dx[4] = { -1,0,1,0 };
int dy[4] = { 0,1,0,-1 };
void dfs(int m,int n){for(int i = 0;i < 4;i++){int a = m + dx[i];int b = n + dy[i];if(vis[a][b]) continue;if(arr[a][b] != '.')continue;//只能走"."if(a < 0 || a >= x) continue;//不能越界if(b < 0 || b >= y) continue;vis[a][b] = true;res++;dfs(a,b);//本题不需要回溯,直接往下搜}
}int main(){ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> y >> x;for (int i = 0; i < x; i++) {for (int j = 0; j < y; j++) {cin >> arr[i][j];}}for (int i = 0; i < x; i++) {for (int j = 0; j < y; j++) {//从起点开始搜索if (arr[i][j] == '@') {vis[i][j] = true;dfs(i, j);}}}cout << res + 1;//加上起点return 0;
}🍃5. 来几道题试试手
🍃5.1 选数
做题点这里👉 : 洛谷P1036

这道题其实还是之前讲过的组合型枚举,例如样例中是4个数里边选3个进行组合,只不过最后多了一个求和和素数判断
还用Java来实现一下:
public class Main {static int n = 0,k = 0;static int cnt = 0;static int[] arr = new int[50];static int[] res = new int[20];public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();k = sc.nextInt();for(int i = 1;i <= n;i++){arr[i] = sc.nextInt();}dfs(1,1);System.out.println(cnt);}public static boolean isPrime(int num){for(int i=2;i*i<=num;i++){if(num%i==0)return false;}return true;}public static void dfs(int x, int start){if(x == k + 1){int sum = 0;//求和for(int i =1;i <= k;i++){sum += res[i];}//判断素数,方案数+1if(isPrime(sum)){cnt++;}return;}for(int i = start;i <= n;i ++){res[x] = arr[i];dfs(x + 1,i + 1);res[x] = 0;}}
}
🍃5.2 火柴棒等式
做题点这里👉 : 洛谷1149

我们来实现一下:
import java.util.Scanner;
public class Main {static int[] match = new int[1000];static int[] arr = new int[1000];static int n = 0, cnt = 0;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();n -= 4;//等号和加号用的火柴棒match[0] = 6;match[1] = 2;match[2] = 5;match[3] = 5;match[4] = 4;match[5] = 5;match[6] = 6;match[7] = 3;match[8] = 7;match[9] = 6;//计算10以后的数字用到的火柴帮数量for (int i = 10; i < 1000; i++) {match[i] = match[i % 10] + match[i / 10];}dfs(1, 0);System.out.println(cnt);}public static void dfs(int x, int sum) {//超过给出的数量,剪枝if (sum > n) {return;}if (x > 3) {if (sum == n && arr[1] + arr[2] == arr[3]) {cnt++;}return;}for (int i = 0; i < 1000; i++) {arr[x] = i;dfs(x + 1, sum + match[i]);arr[x] = 0;}}
}

相关文章:

【DFS(深度优先搜索)详解】看这一篇就够啦
【DFS详解】看这一篇就够啦 🍃1. 算法思想🍃2. 三种枚举方式🍃2.1 指数型枚举🍃2.2 排列型枚举🍃2.3 组合型枚举 🍃3. 剪枝优化🍃4. 图的搜索🍃5. 来几道题试试手🍃5.1 选…...

java-spring boot光速入门教程(超详细!!)
目录 一、引言 1.1 初始化配置 1.2 整合第三方框架 1.3 后期维护 1.4 部署工程 1.5 敏捷式开发 二、SpringBoot介绍 spring boot 2.1 搭建一个spring boot工程 2.2 使用idea创建项目 2.3 在线创建姿势 2.4 项目的目录结构 2.5 项目的运行方式 2.6 yml文件格式 2…...

一、Prometheus和Grafana搭建
一、服务端Prometheus二进制安装 https://prometheus.io/下载过慢可使用迅雷下载 tar -zxvf prometheus-2.53.0.linux-amd64.tar.gz启动 ./prometheus --config.fileprometheus.yml将其配置为系统服务: vim /usr/lib/systemd/system/prometheus.service[Unit] D…...

从零开始的python学习生活
pycharm部分好用快捷键 变量名的定义 与之前学习过的语言有所不同的是,python中变量名的定义更加的简洁 such as 整形。浮点型和字符串的定义 money50 haha13.14 gaga"hello"字符串的定义依然是需要加上引号,也不需要写;了 字符…...

MSP学习
一、迁移资源调研 完成导入,类似完成选型分析 离线工具调研 账单 二、迁移计划 1、 ecs 确认开始构建迁移环境后,平台将锁定当前标记的迁移资源范围及源端、目标端资源配置信息,并以此为迁移环境构建及迁移实施的数据依据 目标账号…...

生产力工具|Endnote X9如何自动更新文件信息
一、以EndNote X9.2版本为例,打开EndNote文献管理软件。 二、在菜单栏找到“Edit→Preferences...”,点击打开,弹出一个“EndNote Preferences”窗口。 三、进行设置 在打开的窗口左侧选择“PDF Handing”,右边会出现自动导入文献…...

【python】字典、列表、集合综合练习
1、练习1(字典) 字典dic,dic {‘k1’:‘v1’, ‘k2’: ‘v2’, ‘k3’: [11,22,33]} (1). 请循环输出所有的key dic {"k1": "v1", "k2": "v2", "k3": [11, 22, 33]} for k in dic.keys():print(k)k1 k2 k3(2). 请循环输…...
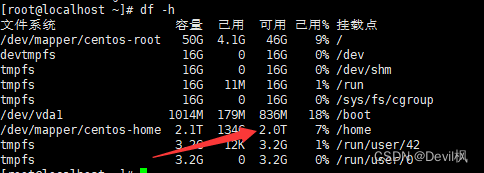
超融合服务器挂载硬盘--linux系统
项目中需要增加服务器的硬盘容量,通过超融合挂载了硬盘后,还需要添加到指定的路径下,这里记录一下操作步骤。 一:通过管理界面挂载硬盘 这一步都是界面操作,登录超融合控制云台后,找到对应的服务器&#…...

Kafka如何防止消息重复发送
Kafka 提供了几种方式来防止消息重复发送和处理。这些方式通常取决于生产者和消费者的设置和实现方式: 生产者端幂等性(什么是幂等性): 幂等性生产者:从 Kafka 0.11 版本开始引入了生产者端的幂等性支持。生产者可以通…...

数据库设计原则介绍
数据库设计是一个重要的过程,它涉及到创建一个逻辑结构来存储和管理数据。良好的数据库设计可以确保数据的完整性、一致性、性能和安全性。以下是一些关键的数据库设计原则: 1. 数据规范化 (Normalization) 目的:减少数据冗余、提高数据一致…...

反馈神经网络与不同类型的神经网络:BP神经网络,深度感知机,CNN,LSTM
反馈神经网络与不同类型的神经网络:BP神经网络,深度感知机,CNN,LSTM 在神经网络的研究和应用中,我们经常听到BP神经网络、深度感知机(MLP)、卷积神经网络(CNN)、长短期记…...

轮播图案例
丐版轮播图 <!DOCTYPE html> <html lang"zh-cn"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title> 基础轮播图 banner 移入移出</t…...

Spring 泛型依赖注入
Spring 泛型依赖注入,是利用泛型的优点对代码时行精简,将可重复使用的代码全部放到一个类之中,方便以后的维护和修改,同时在不增加代码的情况下增加代码的复用性。 示例代码: 创建实体类 Product package test.spri…...
C++ Linux调试(无IDE)
跨平台IDE编译调试C很方便,如QTCreate 、VSCode、Eclipse等,但是如果只能使用Shell控制台呢,gdb调试的优势就很明显了,在没有IDE的情况下,这个方式最有效。因为上手不是很难,特此整理 参考链接 目录 1、G…...

FFmpeg——视频拼接总结
最近需要做一个关于视频拼接的内容,需要将两个视频合成一个视频,使用opencv的话需要将视频读上来然后再写到文件了,这个会很消耗时间也没有必要。两个视频的编码格式是一样的,并不需要转码操作所以想法是直接将视频流补到后面&…...

springboot项目怎么样排除自带tomcat容器使用宝蓝德bes web中间件?
前言: 由于Spring Boot 1.x和2.x不兼容,BES提供了对应的Spring Boot Starter版本。 bes‑lite‑spring‑boot‑1.x‑starter.jar,适用于Spring Boot 1.x的版本。 bes‑lite‑spring‑boot‑2.x‑starter…...
和reactive())
响应式ref()和reactive()
文章目录 ref()reactive()ref对比reactivetoRefs与toRef ref() 作用:定义响应式变量。 语法:let xxxref(初始值)。 返回值:一个RefImpl的实例对象,简称ref对象或ref,ref对象的value属性是响应式的 注意点࿱…...

运维系列.Nginx中使用HTTP压缩功能
运维专题 Nginx中使用HTTP压缩功能 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_28550…...
vue3项目图片压缩+rem+自动重启等plugin使用与打包配置
一、Svg配置 每次引入一张 SVG 图片都需要写一次相对路径,并且对 SVG 图片进行压缩优化也不够方便。 vite-svg-loader插件加载SVG文件作为Vue组件,使用SVGO进行优化。 插件网站https://www.npmjs.com/package/vite-svg-loader 1. 安装 pnpm i vite-svg…...

数据库性能优化系统设计
设计一个数据库性能优化系统,目标是监测、诊断并改善数据库的运行效率,确保系统能够高效稳定地处理大量数据请求。以下是一个概要设计,包括关键模块、功能和实现思路: 1. 系统架构 分布式监控中心:采用分布式架构收集…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

