C++进阶-二叉树进阶(二叉搜索树)
1. 二叉搜索树
1.1 二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 2.若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 3.它的左右子树也分别为二叉搜索树
1.2 二叉搜索树操作

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
- 二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。- 二叉搜索树的插入
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
// 插入节点
// 返回值是布尔型,来判断是否插入成功
// 满足如果key和节点数据相比,小于走左子树,大于走右子树,等于则不插入,返回false
// 而最后结束的时插入到叶子节点
bool Insert(const K& key)
{//判断空树时的情况,直接开辟根节点if (_root == nullptr){// 开辟对象节点空间_root = new Node(key);return true;}// 寻找节点位置,从头结点位置开始寻找Node* cur = _root;// 记录cur的父亲节点Node* parent = nullptr;// 从头结点开始寻找插入的适当位置// 搜索二叉树的原则是满足如果key和节点数据相比// 小于走左子树,大于走右子树,等于则不插入,返回false// 结束条件找到叶子节点的左子树或者右子树(nullptr)while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}else{return false;}}// 开辟节点空间插入cur = new Node(key);if (key < parent->_key){parent->left = cur;}else{parent->right = cur;}return true;
}
- 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面3种情况:
- 一.删除叶子节点(要删除的节点无孩子节点)
- 二.删除左子树或者右子树为空的节点(要删除的结点只有左孩子结点或者只有右孩子节点)
- 三.删除的节点左右子树都不为空(要删除的节点有左、右孩子节点)
首先找到要删除的元素
//每次保留父亲节点,找到并且记录叶子节点
if (key < cur->_key)
{parent = cur;cur = cur->left;
}
else if (key > cur->_key)
{parent = cur;cur = cur->right;
}
else//相等的时候,找到了要删除的位置
{...
}
之后,在else的情况中
实质上在删除的时候的情况:
- 一情况的处理可以与二情况合在一起:
- cur的左子树为空,如果cur在parent左子树,将cur的右子树给parent的左子树,否则cur在parent的右子树,则将cur的右子树付parent的右子树。
- cur的右子树为空,如果cur在parent得到左子树,将cur的左子树付给parent的左子树,否则cur在parent的右子树,则将cur的左子树赋给parent的右子树。
else中也要分为要删除节点的左孩子为空或右孩子为空的情况:
- a.cur的左孩子为空
(1).其中,也要判断是否是头节点,另外判断
(2).cur不是头节点的情况
之后判断cur是parent的哪个孩子
直接将cur的右孩子变为头节点,相当于删除10
根据上面的描述,代码如下
// 左孩子为空if (cur->left == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的右孩子当作头节点_root = cur->right;}else{// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->right;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->right;}}// 删除节点,释放空间delete cur;}
- b.cur的左孩子为空的情况与a情况类似
(1).其中,也要判断是否是头节点,另外判断
(2).cur不是头节点的情况
之后判断cur是parent的哪个孩子
// 内部也分为两种情况:
// 1.是头节点
if (cur == _root)
{// 直接将cur的左孩子当作头节点_root = cur->left;
}
else
{// 2.不是头节点// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->left;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->left;}
}// 删除节点,释放空间
delete cur;
- 2.三情况的解决方式:
删除cur,找一个节点来替换,替换规则:cur的左子树的最大节点,右子树的最小节点,之后交换,直接删除,这种没有问题,在删除头节点会出现问题
所以要更改为交换之后,再要判断rightMin也要分为两种情况,rightMin在rightMinParent左孩子还是右孩子。
else//二.删除的节点左右子树都不为空{// 删除cur,找一个节点来替换// 替换规则:cur的左子树的最大节点,右子树的最小节点,之后交换// 这里用查找右子树的最左节点Node* rightMin = cur->right;Node* rightMinParent = cur;// 开始查找,结束条件左孩子为空,再去找自己,之后右子树while (rightMin->left){rightMinParent = rightMin;rightMin = rightMin->left;}// 交换// 数值交换swap(cur->_key, rightMin->_key);// rightMin也要分为两种情况// 一种是rightMin在rightMinParent左孩子,也就是rightMin左孩子为空if (rightMinParent->left == rightMin)//将rightMin右孩子赋值给父亲节点的左子树rightMinParent->left = rightMin->right;else//另外一种是rightMin在rightMinParent右孩子rightMinParent->right = rightMin->right;delete rightMin;}return true;
}
完成的删除的代码如下:
// 删除:有着三种情况
// 三种情况:1.删除叶子节点 2.删除左子树或者右子树为空的节点 3.删除的节点左右子树都不为空
//一情况的处理可以与二情况合在一起:
//cur的左子树为空,如果cur在parent左子树,将cur的右子树给parent的左子树,否则cur在parent的右子树,则将cur的右子树付parent的右子树
//cur的右子树为空,如果cur在parent得到左子树,将cur的左子树付给parent的左子树,否则cur在parent的右子树,则将cur的左子树赋给parent的右子树
bool erase(const K& key)
{Node* cur = _root;Node* parent = nullptr;// 首先找到需要删除的节点while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}else//相等的时候,找到了要删除的位置{//综合结合为两种情况://一.删除的节点有单个左子树或者右子树为空,或者全为空// 左孩子为空if (cur->left == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的右孩子当作头节点_root = cur->right;}else{// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->right;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->right;}}// 删除节点,释放空间delete cur;}else if (cur->right == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的左孩子当作头节点_root = cur->left;}else{// 2.不是头节点// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->left;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->left;}}// 删除节点,释放空间delete cur;}else//二.删除的节点左右子树都不为空{// 删除cur,找一个节点来替换// 替换规则:cur的左子树的最大节点,右子树的最小节点,之后交换// 这里用查找右子树的最左节点Node* rightMin = cur->right;Node* rightMinParent = cur;// 开始查找,结束条件左孩子为空,再去找自己,之后右子树while (rightMin->left){rightMinParent = rightMin;rightMin = rightMin->left;}// 交换// 数值交换swap(cur->_key, rightMin->_key);// rightMin也要分为两种情况// 一种是rightMin在rightMinParent左孩子,也就是rightMin左孩子为空if (rightMinParent->left == rightMin)//将rightMin右孩子赋值给父亲节点的左子树rightMinParent->left = rightMin->right;else//另外一种是rightMin在rightMinParent右孩子rightMinParent->right = rightMin->right;delete rightMin;}return true;}}return false;}
find的查找代码:
// 查找
bool find(const K& key)
{// 判断为空树时if (_root == nullptr){return false;}Node* cur = _root;while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){cur = cur->left;}else if (key > cur->_key){cur = cur->right;}else{return true;}}return false;
}输出:中序遍历:
这种写法,类外无法访问类内私有成员
更改代码如下:
可进行无参的访问:private中定义有参的,就可以调用私有成员的_root,在类内的public中重载方法InOrder(),在方法内调用有参的。
void InOrder(){InOrder(_root);cout << endl;}private:void InOrder(Node* root){if (root == nullptr){return;}InOrder(root->left);cout << root->_key << " ";InOrder(root->right);}Node* _root = nullptr;//对象指针};
1.3 二叉搜索树的具体实现
1.3.1 K模型
#pragma once
#include<iostream>
using namespace std;
// K模型namespace key
{// 二叉搜索树的实现形式与list类似// 先创建一个节点的类,类中有_key(节点的数据值)、*left(当前节点的左孩子地址)、*right(当前节点的右孩子地址)//节点类template <class K>struct BSTreeNode{K _key;BSTreeNode* left;BSTreeNode* right;//构造函数BSTreeNode(const K& key):_key(key),left(nullptr),right(nullptr){}};// 之后用创建的的节点类,来构造二叉搜索树,每一个节点都是一个节点指针// 二叉搜索树要保证,左孩子值小于父亲节点,右孩子节点大于父亲阶段,数据大小顺序(由小到大):左孩子,父亲,右孩子// 默认定义搜索树不允许冗余// 成员变量为节点指针template<class K>class BSTree{public:// 重命名一下typedef BSTreeNode<K> Node;public:// 构造函数BSTree() :_root(nullptr){}// 插入节点// 返回值是布尔型,来判断是否插入成功// 满足如果key和节点数据相比,小于走左子树,大于走右子树,等于则不插入,返回false// 而最后结束的时插入到叶子节点bool Insert(const K& key){//判断空树时的情况,直接开辟根节点if (_root == nullptr){// 开辟对象节点空间_root = new Node(key);return true;}// 寻找节点位置,从头结点位置开始寻找Node* cur = _root;// 记录cur的父亲节点Node* parent = nullptr;// 从头结点开始寻找插入的适当位置// 搜索二叉树的原则是满足如果key和节点数据相比// 小于走左子树,大于走右子树,等于则不插入,返回false// 结束条件找到叶子节点的左子树或者右子树(nullptr)while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}else{return false;}}// 开辟节点空间插入cur = new Node(key);if (key < parent->_key){parent->left = cur;}else{parent->right = cur;}return true;}// 删除:有着三种情况// 三种情况:1.删除叶子节点 2.删除左子树或者右子树为空的节点 3.删除的节点左右子树都不为空//一情况的处理可以与二情况合在一起://cur的左子树为空,如果cur在parent左子树,将cur的右子树给parent的左子树,否则cur在parent的右子树,则将cur的右子树付parent的右子树//cur的右子树为空,如果cur在parent得到左子树,将cur的左子树付给parent的左子树,否则cur在parent的右子树,则将cur的左子树赋给parent的右子树bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;// 首先找到需要删除的节点while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}else//相等的时候,找到了要删除的位置{//综合结合为两种情况://一.删除的节点有单个左子树或者右子树为空,或者全为空// 左孩子为空if (cur->left == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的右孩子当作头节点_root = cur->right;}else{// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->right;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->right;}}// 删除节点,释放空间delete cur;}else if (cur->right == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的左孩子当作头节点_root = cur->left;}else{// 2.不是头节点// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->left;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->left;}}// 删除节点,释放空间delete cur;}else//二.删除的节点左右子树都不为空{// 删除cur,找一个节点来替换// 替换规则:cur的左子树的最大节点,右子树的最小节点,之后交换// 这里用查找右子树的最左节点Node* rightMin = cur->right;Node* rightMinParent = cur;// 开始查找,结束条件左孩子为空,再去找自己,之后右子树while (rightMin->left){rightMinParent = rightMin;rightMin = rightMin->left;}// 交换// 数值交换swap(cur->_key, rightMin->_key);// rightMin也要分为两种情况// 一种是rightMin在rightMinParent左孩子,也就是rightMin左孩子为空if (rightMinParent->left == rightMin)//将rightMin右孩子赋值给父亲节点的左子树rightMinParent->left = rightMin->right;else//另外一种是rightMin在rightMinParent右孩子rightMinParent->right = rightMin->right;delete rightMin;}return true;}}return false;}// 查找bool find(const K& key){// 判断为空树时if (_root == nullptr){return false;}Node* cur = _root;while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){cur = cur->left;}else if (key > cur->_key){cur = cur->right;}else{return true;}}return false;}// 中序输出(由小到大排序)//类外不能访问私有成员 t1.InOrder(t1._root);/*void InOrder(Node *root){判断是否空树if (root == nullptr){return;}InOrder(root->left);cout << root._key << " ";InOrder(root->right);}*/void InOrder(){InOrder(_root);cout << endl;}private:void InOrder(Node* root){if (root == nullptr){return;}InOrder(root->left);cout << root->_key << " ";InOrder(root->right);}Node* _root = nullptr;//对象指针};}1.3.2 KV模型
#pragma once
#include<iostream>//KV模型(key_value模型)namespace key_value
{//节点类template <class K, class V>struct BSTreeNode{K _key;BSTreeNode<K, V>* left;BSTreeNode<K, V>* right;V _value;//构造函数BSTreeNode(const K& key, const V& value):_key(key),left(nullptr),right(nullptr),_value(value){}};// 之后用创建的的节点类,来构造二叉搜索树,每一个节点都是一个节点指针// 二叉搜索树要保证,左孩子值小于父亲节点,右孩子节点大于父亲阶段,数据大小顺序(由小到大):左孩子,父亲,右孩子// 默认定义搜索树不允许冗余// 成员变量为节点指针template<class K,class V>class BSTree{public:// 重命名一下typedef BSTreeNode<K,V> Node;public:// 构造函数BSTree() :_root(nullptr){}// 插入节点// 返回值是布尔型,来判断是否插入成功// 满足如果key和节点数据相比,小于走左子树,大于走右子树,等于则不插入,返回false// 而最后结束的时插入到叶子节点bool Insert(const K& key, const V& value){//判断空树时的情况,直接开辟根节点if (_root == nullptr){// 开辟对象节点空间_root = new Node(key, value);return true;}// 寻找节点位置,从头结点位置开始寻找Node* cur = _root;// 记录cur的父亲节点Node* parent = nullptr;// 从头结点开始寻找插入的适当位置// 搜索二叉树的原则是满足如果key和节点数据相比// 小于走左子树,大于走右子树,等于则不插入,返回false// 结束条件找到叶子节点的左子树或者右子树(nullptr)while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}else{return false;}}// 开辟节点空间插入cur = new Node(key, value);if (key < parent->_key){parent->left = cur;}else{parent->right = cur;}return true;}// 删除:有着三种情况// 三种情况:1.删除叶子节点 2.删除左子树或者右子树为空的节点 3.删除的节点左右子树都不为空//一情况的处理可以与二情况合在一起://cur的左子树为空,如果cur在parent左子树,将cur的右子树给parent的左子树,否则cur在parent的右子树,则将cur的右子树付parent的右子树//cur的右子树为空,如果cur在parent得到左子树,将cur的左子树付给parent的左子树,否则cur在parent的右子树,则将cur的左子树赋给parent的右子树bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;// 首先找到需要删除的节点while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}else//相等的时候,找到了要删除的位置{//综合结合为两种情况://一.删除的节点有单个左子树或者右子树为空,或者全为空// 左孩子为空if (cur->left == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的右孩子当作头节点_root = cur->right;}else{// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->right;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->right;}}// 删除节点,释放空间delete cur;}else if (cur->right == nullptr){// 内部也分为两种情况:// 1.是头节点if (cur == _root){// 直接将cur的左孩子当作头节点_root = cur->left;}else{// 2.不是头节点// 判断cur是parent的哪个孩子//cur是parent左孩子if (cur == parent->left){//cur的右子树赋给parent的左子树parent->left = cur->left;}else// cur是parent右孩子时{//cur的右子树赋给parent的右子树parent->right = cur->left;}}// 删除节点,释放空间delete cur;}else//二.删除的节点左右子树都不为空{// 删除cur,找一个节点来替换// 替换规则:cur的左子树的最大节点,右子树的最小节点,之后交换// 这里用查找右子树的最左节点Node* rightMin = cur->right;Node* rightMinParent = cur;// 开始查找,结束条件左孩子为空,再去找自己,之后右子树while (rightMin->left){rightMinParent = rightMin;rightMin = rightMin->left;}// 交换// 数值交换swap(cur->_key, rightMin->_key);// rightMin也要分为两种情况// 一种是rightMin在rightMinParent左孩子,也就是rightMin左孩子为空if (rightMinParent->left == rightMin)//将rightMin右孩子赋值给父亲节点的左子树rightMinParent->left = rightMin->right;else//另外一种是rightMin在rightMinParent右孩子rightMinParent->right = rightMin->right;delete rightMin;}return true;}}return false;}// 查找Node* find(const K& key){Node* cur = _root;while (cur){//每次保留父亲节点,找到并且记录叶子节点if (key < cur->_key){cur = cur->left;}else if (key > cur->_key){cur = cur->right;}else{// 找到了返回节点return cur;}}//没找到,返回节点,此时节点为空return cur;}// 中序输出(由小到大排序)// 类外不能访问私有成员 t1.InOrder(t1._root);//void InOrder(Node *root)//{// // 判断是否空树// if (root == nullptr)// {// return;// }// InOrder(root->left);// cout << root._key << " ";// InOrder(root->right);//}void InOrder(){InOrder(_root);cout << endl;}private:void InOrder(Node* root){if (root == nullptr){return;}InOrder(root->left);cout << root->_key << ":" << _root->_value;InOrder(root->right);}Node* _root = nullptr;//对象指针};void TestBSTree2(){BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("left", "左边");dict.Insert("insert", "插入");//...string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.find(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词,请重新输入" << endl;}}}void TestBSTree3(){// 统计次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉","苹果","草莓", "苹果","草莓" };BSTree<string, int> countTree;for (const auto& str : arr){auto ret = countTree.find(str);if (ret == nullptr){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();}
}
1.4 二叉搜索树的应用
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。- KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
该种方式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
1.5 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: l o g 2 N log_2 N log2N
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?那么我们后续章节学习的AVL树和红黑树就可以上场了。
相关文章:

C++进阶-二叉树进阶(二叉搜索树)
1. 二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值2.若它的右子树不为空,则右子树上所有节点的值都大于…...

【Unity小知识】UnityEngine.UI程序集丢失的问题
问题表现 先来说一下问题的表现,今天在开发的时候工程突然出现了报错,编辑器提示UnityEngine.UI缺少程序集引用。 问题分析与解决(一) 既然是程序集缺失,我们首先查看一下工程项目是否引用了程序集。在项目引用中查找一…...

CentOS 离线安装部署 MySQL 8详细教程
1、简介 MySQL是一个流行的开源关系型数据库管理系统(RDBMS),它基于SQL(Structured Query Language,结构化查询语言)进行操作。MySQL最初由瑞典的MySQL AB公司开发,后来被Sun Microsystems公司…...

云计算【第一阶段(28)】DNS域名解析服务
一、DNS解析的定义与作用 1.1、DNS解析的定义 DNS解析(Domain Name System Resolution)是互联网服务中的一个核心环节,它负责将用户容易记住的域名转换成网络设备能够识别和使用的IP地址。一般来讲域名比 IP 地址更加的有含义、也更容易记住…...

pygame 音乐粒子特效
代码 import pygame import numpy as np import pymunk from pymunk import Vec2d import random import librosa import pydub# 初始化pygame pygame.init()# 创建屏幕 screen pygame.display.set_mode((1920*2-10, 1080*2-10)) clock pygame.time.Clock()# 加载音乐文件 a…...

Leetcode 295.数据流的中位数
295.数据流的中位数 问题描述 中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。 例如 arr [2,3,4] 的中位数是 3 。例如 arr [2,3] 的中位数是 (2 3) / 2 2.5 。 实现 MedianFinder 类: Media…...

A59 STM32_HAL库函数 之 TIM扩展驱动 -- A -- 所有函数的介绍及使用
A59 STM32_HAL库函数 之 TIM扩展驱动 -- A -- 所有函数的介绍及使用 1 该驱动函数预览1.1 HAL_TIMEx_HallSensor_Init1.2 HAL_TIMEx_HallSensor_DeInit1.3 HAL_TIMEx_HallSensor_MspInit1.4 HAL_TIMEx_HallSensor_MspDeInit1.5 HAL_TIMEx_HallSensor_Start1.6 HAL_TIMEx_HallSe…...
【Unity】UGUI的基本介绍
Unity的UGUI(Unity User Interface)是Unity引擎内自带的UI系统,官方称之为UnityUI,是目前Unity商业游戏开发中使用最广泛的UI系统开发解决方案。以下是关于Unity的UGUI的详细介绍: 一、UGUI的特点 灵活性:…...

MySQL 9.0新特性:向量存储
MySQL 9.0 正式版已经发布,其中一个亮点就是向量(VECTOR)数据类型的支持,本文给大家详细介绍一下这个新功能。 向量类型 MySQL 9.0 增加了一个新的向量数据类型:VECTOR。它是一种可以存储 N 个数据项的数据结构&…...
选择数据源及非标准使用数据库)
ruoyi实用性改造--(四)选择数据源及非标准使用数据库
一、实用型数据直接访问/** 使用Druid中 application-druid.yml 中定义的副数据源Connection con=null; //手工调用Druid的配置访问Connection con2=null;try {//DruidDataSource ds = SpringUtils.getBean("masterDataSource");DruidDataSource ds = Spring…...

HMI 的 UI 风格创造奇迹
HMI 的 UI 风格创造奇迹...
如何安全隐藏IP地址,防止网络攻击?
当您想在互联网上保持隐私或匿名时,您应该做的第一件事就是隐藏您的 IP 地址。您的 IP 地址很容易被追踪到您,并被用来了解您的位置。下面的文章将教您如何隐藏自己,不让任何试图跟踪您的活动的人发现。 什么是 IP 地址? 首先&am…...

Windows10/11家庭版开启Hyper-V虚拟机功能详解
Hyper-V是微软的一款虚拟机软件,可以使我们在一台Windows PC上,在虚拟环境下同时运行多个互相之间完全隔离的操作系统,这就实现了在Windows环境下运行Linux以及其他OS的可能性。和第三方虚拟机软件,如VMware等相比,Hyp…...

202487读书笔记|《我有个拥抱,你要不要》——生活从来如此,你的态度赋予它意义
202487读书笔记|《我有个拥抱,你要不要》——生活从来如此,你的态度赋予它意义 《我有个拥抱,你要不要》作者一天到晚气fufu,挺有愛的小漫画,适合用来看图说话锻炼小语言,我看的很快乐也写得很痛快…...
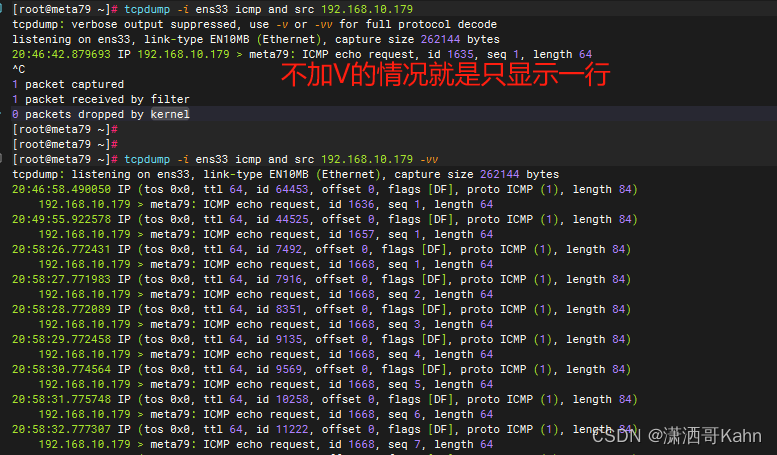
使用tcpdump抓取本本机的所有icmp包
1、抓取本机所有icmp包 tcpdump -i any icmp -vv 图中上半部分,是源主机tmp179无法ping通目标主机192.168.10.79(因为把该主机关机了)的状态,注意看,其中有unreachable 图中下半部分,是源主机tmp179可以p…...

Nginx:负载均衡小专题
运维专题 Nginx:负载均衡小专题 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/…...

新增多种图表类型,新增插件管理模块,DataEase开源数据可视化分析工具v2.8.0发布
2024年7月8日,人人可用的开源数据可视化分析工具DataEase正式发布v2.8.0版本。 这一版本的功能变动包括:图表方面,新增组合图、热力地图、符号地图、K线图等图表类型,并对已有的仪表盘、明细表、指标卡、富文本等图表类型进行了功…...
android perfetto使用技巧梳理
1 抓取方法 根据不同的配置参数,会显示不同的功能。 比如有的trace文件就无法显示线程状态信息,有的无法显示锁依赖信息等等,要看你的参数,我这个是很全的,基本够了,如果还想添加,可以命令行看…...

bond网络配置文件中zone
在bond网络配置文件中,zone是一个参数,用于指定bond设备所属的防火墙安全区域。它可以设置为一个字符串值,通常是一个自定义的区域名称。 防火墙安全区域是一种网络隔离和安全策略的概念,它可以将网络划分为不同的区域࿰…...

spring事务详解
事务管理方式 在Spring中,事务有两种实现方式,分别是编程式事务管理和声明式事务管理两种方式。 编程式事务管理: 编程式事务管理使用TransactionTemplate或者直接使用底层的PlatformTransactionManager。对于编程式事务管理,sp…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...











