【手撕数据结构】卸甲时/空间复杂度
目录
- 前言
- 时间复杂度
- 概念
- ⼤O的渐进表⽰法
- 小试牛刀
- 空间复杂度
前言
要想知道什么是空/时间复杂度,就得知道什么是数据结构。
这得分两层来理解。我们生活中处处存在数据,什么抖音热点上的国际大事,什么懂的都懂的雍正卸甲等等一系列我们用户看得到的,就是抖音存储在后台服务器的数据。但这些数据都有一个特点,那就是都在抖音的热搜榜单上,而这个榜单就是结构,保证数据在一个固定的位置里以便用户浏览。
此外有了数据结构,就离不开算法。那么我们刚刚说了,数据结构是把数据有规律的存储在一个结构中,那么怎么从结构中有效率的存取数据,这就是算法。
时间复杂度
有了算法,就存在时间复杂度和空间复杂度。因为计算机现在的内存越来越大,所以时间复杂度比空间复杂度更显得重要。所以我们先来了解时间复杂度
概念
时间复杂度,最重要的词就是时间,这里的时间就是指一个程序运行时的时间,如果时间复杂度越少,那么证明这个算法越好。时间复杂度计算用函数式T(N)表示
那为什么我们不提前算出这个程序的时间复杂度来写出最优解的代码呢?这里就涉及到计算机的问题。
- 因为程序运⾏时间和编译环境和运⾏机器的配置都有关系,⽐如同⼀个算法程序,⽤⼀个⽼编译
器进⾏编译和新编译器编译,在同样机器下运⾏时间不同。- 同⼀个算法程序,⽤⼀个⽼低配置机器和新⾼配置机器,运⾏时间也不同。
- 并且时间只能程序写好后测试,不能写程序前通过理论思想计算评估。
下面我们来看一段代码:
// 请计算⼀下Func1中count语句总共执⾏了多少
次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
}
这段代码如果根据count的执行次数来看的话应该是:
T (N) = N2 + 2 ∗ N + 10
• N = 10 T(N) = 130
• N = 100 T(N) = 10210
• N = 1000 T(N) = 1002010
这时候有人就说,那个int count=0不算吗;
这里我们就太小看我们的计算机了,我们计算机一秒钟cpu可以执行上亿次,这小小的一次当然可以忽略不计。所以说我们计算的时间复杂度并不准确,只是粗略估计而已,这时候我们就用一个新的符号表示.
⼤O的渐进表⽰法
⼤O符号(Big O notation):是⽤于描述函数渐进⾏为的数学符号;这里用来表示估算的时间复杂度。
那么这里还是跟T(N)一样算吗,如果是这样我们就没必要用另外一个符号来表示了。这里就涉及到算O的规则:
- 时间复杂度函数式T(N)中,只保留最⾼阶项,去掉那些低阶项,因为当N不断变⼤时,低阶项对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。
- 如果最⾼阶项存在且不是1,则去除这个项⽬的常数系数,因为当N不断变⼤,这个系数对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了
- T(N)中如果没有N相关的项⽬,只有常数项,⽤常数1取代所有加法常数。
那么再来看上面的T(N)=N^ 2 + 2 ∗ N + 10,这里的最高阶是N2所以去掉其他的低阶,复杂度就为(ON^2)
小试牛刀
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++
k)
{
++count;
}
printf("%d\n", count);
}
这里的T(N)=M+N,那我们再来算O(N),这里M和N都是同阶,所以不符合第一条规则,也没有对应第二条和第三条,所以为o(N+M),那么有人就问了,万一N比M大呢,是不是因该是O(N).这里问题就是,你怎么知道N比M大?万一是M比N大呢,所以保险起见我们都留下来。
// 计算strchr的时间复杂度?
const char * strchr ( const char* str, int character)
{
const char* p_begin = s;
while (*p_begin != character)
{
if (*p_begin == '\0')
return NULL;
p_begin++;
}
return p_begin;
}
这里我们是查找character在str中的位置,这里我补充一个知识点:
- 我们的O算的一般是一个算法的最坏情况下的复杂度
这里就可以分为三个复杂度:
1.最好情况
若要查找的字符在字符串第⼀个位置,则:
F (N) = 1,复杂度为o(1)
2.平均情况:
若要查找的字符在字符串中间位置,则:
F (N) = N/2,O(N/2)
3.最坏情况
若要查找的字符在字符串最后的⼀个位置,则:
F (N) = N,O(N)
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}

最坏情况下,又因为保留高阶去掉n/2(第一条),忽略系数(第二条),所以为ON^2
void func5(int n)
{
int cnt = 1;
while (cnt < n)
{
cnt *= 2;
}
}
当n=2时,执⾏次数为1
当n=4时,执⾏次数为2
当n=16时,执⾏次数为4
假设执⾏次数为 x ,则 2
x = n
因此执⾏次数: x = log n
因此:func5的时间复杂度取最差情况为:
O(log2 ^n)
不同书籍的表⽰⽅式不同,以上写法差别不⼤,我们建议使⽤ log n
空间复杂度
空间复杂度要注意的是,他的计算表示也是用O来表示,并且他的规则与时间复杂度一样遵守那三条规则
注意
函数运⾏时所需要的栈空间(存储参数、局部变量、⼀些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运⾏时候显式申请的额外空间来确定
例1:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
函数栈帧在编译期间已经确定好了,
只需要关注函数在运⾏时额外申请的空间。
BubbleSort额外申请的空间有
exchange等有限个局部变量,使⽤了常数个额外空间
因此空间复杂度为 O(1)
相关文章:

【手撕数据结构】卸甲时/空间复杂度
目录 前言时间复杂度概念⼤O的渐进表⽰法小试牛刀 空间复杂度 前言 要想知道什么是空/时间复杂度,就得知道什么是数据结构。 这得分两层来理解。我们生活中处处存在数据,什么抖音热点上的国际大事,什么懂的都懂的雍正卸甲等等一系列我们用户看得到的&a…...

消防认证-防火窗
一、消防认证 消防认证是指消防产品符合国家相关技术要求和标准,且通过了国家认证认可监督管理委员会审批,获得消防认证资质的认证机构颁发的证书,消防产品具有完好的防火功能,是住房和城乡建设领域验收的重要指标。 二、认证依据…...

C++进阶-二叉树进阶(二叉搜索树)
1. 二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值2.若它的右子树不为空,则右子树上所有节点的值都大于…...

【Unity小知识】UnityEngine.UI程序集丢失的问题
问题表现 先来说一下问题的表现,今天在开发的时候工程突然出现了报错,编辑器提示UnityEngine.UI缺少程序集引用。 问题分析与解决(一) 既然是程序集缺失,我们首先查看一下工程项目是否引用了程序集。在项目引用中查找一…...

CentOS 离线安装部署 MySQL 8详细教程
1、简介 MySQL是一个流行的开源关系型数据库管理系统(RDBMS),它基于SQL(Structured Query Language,结构化查询语言)进行操作。MySQL最初由瑞典的MySQL AB公司开发,后来被Sun Microsystems公司…...

云计算【第一阶段(28)】DNS域名解析服务
一、DNS解析的定义与作用 1.1、DNS解析的定义 DNS解析(Domain Name System Resolution)是互联网服务中的一个核心环节,它负责将用户容易记住的域名转换成网络设备能够识别和使用的IP地址。一般来讲域名比 IP 地址更加的有含义、也更容易记住…...

pygame 音乐粒子特效
代码 import pygame import numpy as np import pymunk from pymunk import Vec2d import random import librosa import pydub# 初始化pygame pygame.init()# 创建屏幕 screen pygame.display.set_mode((1920*2-10, 1080*2-10)) clock pygame.time.Clock()# 加载音乐文件 a…...

Leetcode 295.数据流的中位数
295.数据流的中位数 问题描述 中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。 例如 arr [2,3,4] 的中位数是 3 。例如 arr [2,3] 的中位数是 (2 3) / 2 2.5 。 实现 MedianFinder 类: Media…...

A59 STM32_HAL库函数 之 TIM扩展驱动 -- A -- 所有函数的介绍及使用
A59 STM32_HAL库函数 之 TIM扩展驱动 -- A -- 所有函数的介绍及使用 1 该驱动函数预览1.1 HAL_TIMEx_HallSensor_Init1.2 HAL_TIMEx_HallSensor_DeInit1.3 HAL_TIMEx_HallSensor_MspInit1.4 HAL_TIMEx_HallSensor_MspDeInit1.5 HAL_TIMEx_HallSensor_Start1.6 HAL_TIMEx_HallSe…...
【Unity】UGUI的基本介绍
Unity的UGUI(Unity User Interface)是Unity引擎内自带的UI系统,官方称之为UnityUI,是目前Unity商业游戏开发中使用最广泛的UI系统开发解决方案。以下是关于Unity的UGUI的详细介绍: 一、UGUI的特点 灵活性:…...

MySQL 9.0新特性:向量存储
MySQL 9.0 正式版已经发布,其中一个亮点就是向量(VECTOR)数据类型的支持,本文给大家详细介绍一下这个新功能。 向量类型 MySQL 9.0 增加了一个新的向量数据类型:VECTOR。它是一种可以存储 N 个数据项的数据结构&…...
选择数据源及非标准使用数据库)
ruoyi实用性改造--(四)选择数据源及非标准使用数据库
一、实用型数据直接访问/** 使用Druid中 application-druid.yml 中定义的副数据源Connection con=null; //手工调用Druid的配置访问Connection con2=null;try {//DruidDataSource ds = SpringUtils.getBean("masterDataSource");DruidDataSource ds = Spring…...

HMI 的 UI 风格创造奇迹
HMI 的 UI 风格创造奇迹...
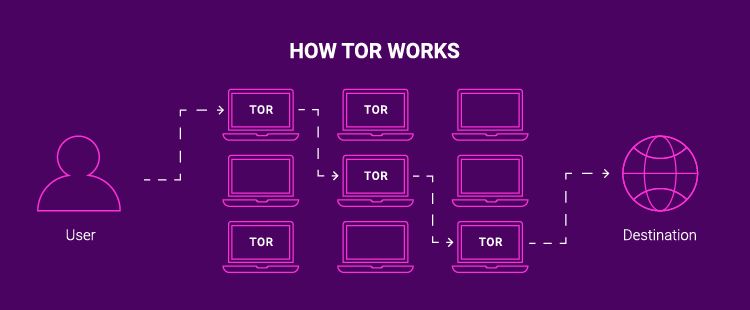
如何安全隐藏IP地址,防止网络攻击?
当您想在互联网上保持隐私或匿名时,您应该做的第一件事就是隐藏您的 IP 地址。您的 IP 地址很容易被追踪到您,并被用来了解您的位置。下面的文章将教您如何隐藏自己,不让任何试图跟踪您的活动的人发现。 什么是 IP 地址? 首先&am…...

Windows10/11家庭版开启Hyper-V虚拟机功能详解
Hyper-V是微软的一款虚拟机软件,可以使我们在一台Windows PC上,在虚拟环境下同时运行多个互相之间完全隔离的操作系统,这就实现了在Windows环境下运行Linux以及其他OS的可能性。和第三方虚拟机软件,如VMware等相比,Hyp…...

202487读书笔记|《我有个拥抱,你要不要》——生活从来如此,你的态度赋予它意义
202487读书笔记|《我有个拥抱,你要不要》——生活从来如此,你的态度赋予它意义 《我有个拥抱,你要不要》作者一天到晚气fufu,挺有愛的小漫画,适合用来看图说话锻炼小语言,我看的很快乐也写得很痛快…...
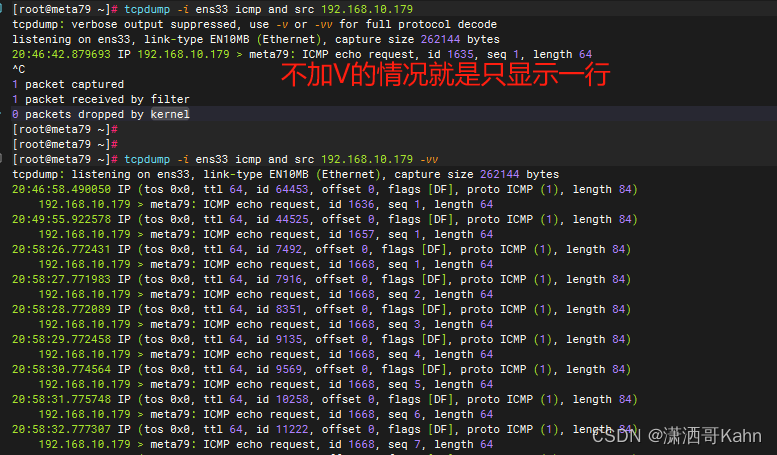
使用tcpdump抓取本本机的所有icmp包
1、抓取本机所有icmp包 tcpdump -i any icmp -vv 图中上半部分,是源主机tmp179无法ping通目标主机192.168.10.79(因为把该主机关机了)的状态,注意看,其中有unreachable 图中下半部分,是源主机tmp179可以p…...

Nginx:负载均衡小专题
运维专题 Nginx:负载均衡小专题 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/…...

新增多种图表类型,新增插件管理模块,DataEase开源数据可视化分析工具v2.8.0发布
2024年7月8日,人人可用的开源数据可视化分析工具DataEase正式发布v2.8.0版本。 这一版本的功能变动包括:图表方面,新增组合图、热力地图、符号地图、K线图等图表类型,并对已有的仪表盘、明细表、指标卡、富文本等图表类型进行了功…...
android perfetto使用技巧梳理
1 抓取方法 根据不同的配置参数,会显示不同的功能。 比如有的trace文件就无法显示线程状态信息,有的无法显示锁依赖信息等等,要看你的参数,我这个是很全的,基本够了,如果还想添加,可以命令行看…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
