代码随想录算法训练营:20/60
非科班学习算法day20 | LeetCode235:二叉搜索树的最近公共祖先 ,Leetcode701:二叉树的插入操作 ,Leetcode450:删除二叉搜索树的节点
介绍
包含LC的两道题目,还有相应概念的补充。
相关图解和更多版本:
代码随想录 (programmercarl.com)https://programmercarl.com/#%E6%9C%AC%E7%AB%99%E8%83%8C%E6%99%AF
一、LeetCode题目
1.LeetCode235:二叉搜索树的最近公共祖先
题目链接:235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
题目解析
和普通二叉树最大的区别就是搜索树是有序的,那么我们可以
c++代码如下:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/class Solution {
public:// 和普通二叉树比,肯定是不用遍历全部树// 那么怎样才可以找到结果呢TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (!root)return NULL;if (root->val == p->val || root->val == q->val) {return root;}if (root->val > p->val && root->val > q->val) {return lowestCommonAncestor(root->left, p, q);}if (root->val < p->val && root->val < q->val) {return lowestCommonAncestor(root->right, p, q);} elsereturn root;}
};注意点1:
2.Leetcode701:二叉搜索树的插入操作
题目链接:701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
题目解析
根据二叉搜索树的性质,可以进行单边搜索。题目中说任意的插入类型都可以,那么遇到空节点进行插入,而不需要调整树的结构。
C++代码如下:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (!root) {TreeNode* new_node = new TreeNode(val);return new_node;}if (root->val > val)root->left = insertIntoBST(root->left, val);if (root->val < val)root->right = insertIntoBST(root->right, val);return root;}
};注意点:搜索二叉树通常是单边搜索,那么这时候需要用值“接住”我们的递归函数;而且我们要明确,在这道题中递归是向下的,返回的类型是节点,节点可以拼接在上一层的节点上,这就是递归寻找的思路
3.Leetcode450:删除二叉搜索树中的节点
题目链接:450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
题目解析
删除的操作一定涉及到树的结构改变,但是通过自己画图理解可以发现,删除的不过是叶子节点或者中间(根)节点,那么就要分情况处理每一种,而且对于递归的逻辑就是我们需要返回需要的节点,将节点接住,构成新的树
C++代码如下:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:// 必有结构调整TreeNode* deleteNode(TreeNode* root, int key) {// 中止条件if (!root)return root;// 删除条件if (root->val == key) {// 模拟情况-左节点空右节点空if (!root->left && !root->right) {delete root;return nullptr;}// 模拟情况-左节点空右节点非空if (!root->left && root->right) {auto temp = root->right;delete root;return temp;} // return root->right;// 模拟情况-右节点空左节点非空if (!root->right && root->left) {auto temp = root->left;delete root;return temp;} // return root->left;// 模拟情况-左节点非空右节点非空if (root->left && root->right) {TreeNode* cur = root->right;while (cur->left != nullptr) {cur = cur->left;}cur->left = root->left;TreeNode* to_del = root;root = root->right;delete to_del;return root;}}if (root->val < key)root->right = deleteNode(root->right, key);if (root->val > key)root->left = deleteNode(root->left, key);return root;}
};注意点1:这里分情况是根据左右孩子节点的情况分类,因为找到需要的值之后,要根据他的节点情况将整颗孩子树移动;对于两边都不为空的节点,这里是将右节点作为补位的节点,实际上左节点也可以。
总结
打卡第20天,坚持!!!
相关文章:

代码随想录算法训练营:20/60
非科班学习算法day20 | LeetCode235:二叉搜索树的最近公共祖先 ,Leetcode701:二叉树的插入操作 ,Leetcode450:删除二叉搜索树的节点 介绍 包含LC的两道题目,还有相应概念的补充。 相关图解和更多版本: 代码随想录 (programmer…...

Apache Seata应用侧启动过程剖析——RM TM如何与TC建立连接
本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 Apache Seata应用侧启动过程剖析——RM & TM如何与TC建立连接 前言 看过官网 README 的第…...

Origin 的使用
官网:OriginLab - Origin and OriginPro - Data Analysis and Graphing Software 安装:Origin2022最新最详细的安装教程 学生免费:Origin 官方正版免费续期教程 更改语言:解决OriginPro2024学生版本的更改中文change language灰…...

MySQL相关知识点
目录 1. 基本概念2. 数据类型3. 数据库操作4. 表操作5. 数据操作6. 索引7. 约束8. 事务9. 存储过程和触发器10. 优化和性能调优11. 安全性12. 备份和恢复 MySQL 是一个广泛使用的 关系数据库管理系统 (RDBMS)。了解 MySQL 的主要知识点可以帮助你更好地设计、管理和优化数据库…...
)
第4章 Vite模块化与插件系统(二)
4.3 常用插件介绍 4.3.1 官方插件 vitejs/plugin-vue 用于支持 Vue.js 开发: npm install vitejs/plugin-vue --save-devimport vue from vitejs/plugin-vueexport default defineConfig({plugins: [vue()] })vitejs/plugin-react 用于支持 React 开发…...

前端传到后端的data数组中有些属性值为空
将前端输入框中的值全部放入data中传入后端,但是在后端查看发现后端接收到的数据有些属性值为空。 第一种情况:只有第一个属性为空,其余属性接收正常 可能原因:后端用来接收的 比如前端发送数据: 实际上前端发送的数…...
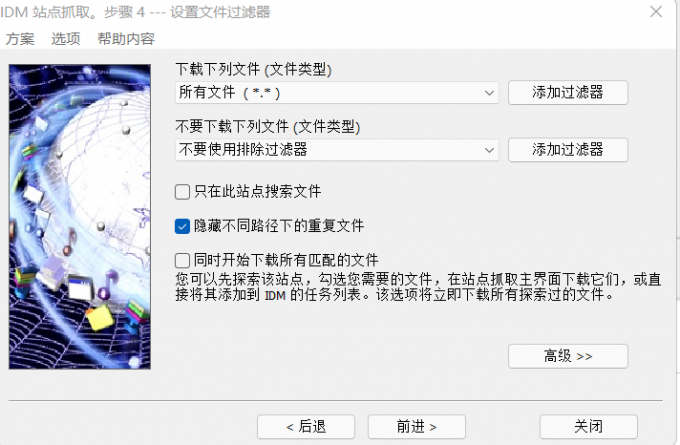
怎么批量下载网页里的图片和视频 如何批量下载一个网站的所有图片 如何批量下载网页视频文件 idm软件怎么下载
当我们在网站内需要下载大量图片时,一张一张的下载非常麻烦。这里推荐大家使用IDM这款网页图片下载工具。下面,我将介绍怎么批量下载网页里的图片和视频,如何批量下载一个网站的所有图片的解决方法。 一、怎么批量下载网页里的图片和视频 …...

Python面试题:在 Python 中,如何处理文件操作?
在Python中,文件操作(如读取和写入文件)是一个常见的任务。Python标准库提供了内置的函数和上下文管理器来简化文件操作。以下是处理文件操作的一些基本方法和示例: 打开和关闭文件 使用open()函数打开文件。该函数返回一个文件…...

红日靶机1
靶场环境 使用kali攻击web服务器,然后根据web服务器攻击其他域内的机器 这里很明确kali是攻击机,外网机器,局域网中的win7是web服务器,有2个网卡,通内网和外网,2k3以及2008r2是内网机器,不出网&…...

Windows电脑PC使用adb有线跟无线安装apk包
在Android开发中,经常需要使用ADB(Android Debug Bridge)来安装APK包到Android设备上,无论是通过有线连接还是无线连接。以下将分别介绍如何通过有线和无线方式使用ADB安装APK包。 有线连接安装APK 启用开发者选项和USB调试&…...

如何把harmonos项目修改为openharmony项目
一开始分不清harmonyos和openharmony,在harmonyos直接下载的开发软件,后面发现不对劲,打脑阔 首先你要安装对应版本的开发软件,鸿蒙开发是由harmonyos和openharmony官网两个的,找到对应的地方下载对应版本的开发软件&…...

【QT】Qt智能指针QPointer、QSharedPointer、QWeakPointer、QScopedPointer
QPointer QPointer can only point to QObject instances. It will be automatically set to nullptr if the pointed to object is destroyed. It is a weak pointer specialized for QObject. QPointer只能指向QObject实例。如果指向的对象被销毁,它将自动设置为 …...

设计模式探索:建造者模式
1. 什么是建造者模式 建造者模式 (Builder Pattern),也被称为生成器模式,是一种创建型设计模式。 定义:将一个复杂对象的构建与表示分离,使得同样的构建过程可以创建不同的表示。 建造者模式要解决的问题: 建造者模…...

[Go] 字符串遍历数据类型问题
字符串遍历问题 在使用for i,v:range str遍历字符串时 str[i]是unit8(byte)类型,返回的是单个字节 字符串在Go中是以字节序列的形式存储的,而 str[i] 直接访问了这个字节序列中的第 i 个字节。如果字符串中的字符是单字节的ASCII…...

HJ41 称砝码
HJ41 称砝码 提示:文章 文章目录 前言一、背景二、 2.1 2.2 总结 前言 前期疑问: 本文目标: 一、背景 这个题目之前是没有做出来的,我把之前没做出来的代码也记录一下 二、 2.1 之前的代码 #include <stdio.h>int m…...
如何使用Python脚本实现SSH登录
调试IDE:PyCharm Python库:Paramiko 首先安装Paramiko包到PyCharm,具体步骤为:在打开的PyCharm工具中,选择顶部菜单栏中“File”下的“Settings”,在设置对话框中,选择“Project”下的“Proje…...

2024年文化研究与数字媒体国际会议 (CRDM 2024)
2024年文化研究与数字媒体国际会议 (CRDM 2024) 2024 International Conference on Cultural Research and Digital Media 【重要信息】 大会地点:珠海 大会官网:http://www.iccrdm.com 投稿邮箱:iccrdmsub-conf.com 【注意:稿将…...

14-52 剑和诗人26 - RAG 和 VectorDB 简介
检索增强生成 (RAG) 和 VectorDB 是自然语言处理 (NLP) 中的两个重要概念,它们正在突破 AI 系统所能实现的界限。 在这篇博文中,我将深入探讨 RAG,探索其工作原理、应用、优势和局限性。 我们还将研究 VectorDB,这是一种专用于向…...

如果MySQL出现 “Too many connections“ 错误,该如何解决?
当你想要连接MySQL时出现"Too many connections" 报错的情况下,该如何解决才能如愿以偿呢?都是哥们儿,就教你两招吧! 1.不想重启数据库的情况下 你可以尝试采取以下方法来解决: 增加连接数限制:…...

论文阅读:Rethinking Interpretability in the Era of Large Language Models
Rethinking Interpretability in the Era of Large Language Models 《Rethinking Interpretability in the Era of Large Language Models》由Chandan Singh、Jeevana Priya Inala、Michel Galley、Rich Caruana和Jianfeng Gao撰写,探讨了在大型语言模型ÿ…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
