C#委托事件的实现
1、事件
在C#中事件是一种特殊的委托类型,用于在对象之间提供一种基于观察者模式的通知机制。
1.1、事件的发送方定义了一个委托,委托类型的声明包含了事件的签名,即事件处理器方法的签名。
1.2、事件的订阅者可以通过+=运算符来注册事件处理器。
1.3、当事件发送方触发事件时,所有注册的事件处理器会被依次调用。
2、委托事件的实现
2.1、事件发布类
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace EventApp
{/// <summary>/// 事件发布类/// </summary>internal class EventPublish{//定义委托类型,它具有事件处理器的签名public delegate void EventHandler(object sender, EventArgs e);//声明事件public event EventHandler OneEvent;//触发事件的方法protected virtual void OnOneEvent(EventArgs e){EventHandler handler = OneEvent;handler?.Invoke(this, e);}//示例方法,可以在需要的时候触发事件public void TriggerEvent(){OnOneEvent(EventArgs.Empty);}}
}
2.1、事件订阅类
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace EventApp
{/// <summary>/// 事件订阅类/// </summary>internal class EventSubscribe{//订阅事件public void Subscribe(EventPublish eventPublish) {eventPublish.OneEvent += EventPublish_OneEvent;}//事件处理函数private void EventPublish_OneEvent(object sender, EventArgs e){Console.WriteLine("Event is triggered!");}}
}
2.3、委托事件的实现
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Threading.Tasks;namespace EventApp
{internal class Program{static void Main(string[] args){EventPublish eventPublish = new EventPublish();EventSubscribe eventSubscribe = new EventSubscribe();//订阅事件eventSubscribe.Subscribe(eventPublish);Console.Write("Press <Enter> to trigger event\n");while (Console.ReadKey().Key != ConsoleKey.Enter) { Thread.Sleep(100); }//触发事件eventPublish.TriggerEvent();Console.ReadKey();}}
}
3、代码说明
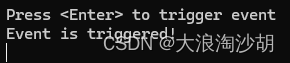
在这个例子中,EventPublish 类定义了一个委托 EventHandler 和一个基于该委托类型的事件 OneEvent。OnOneEvent 方法是触发事件的方法,它检查事件是否有注册的处理器,并按顺序调用它们。TriggerEvent 方法用于触发事件。EventSubscribe 类中的 Subscribe 方法用于订阅事件,并提供了事件处理器 EventHandler。在 Main 方法中,我们创建了 EventPublish 和 EventSubscribe 的实例,并通过 Subscribe 方法将 EventHandler 注册到 OneEvent 上。最后通过 TriggerEvent 方法触发了事件,控制台上输出了 “Event is triggered!”。
4、运行效果
相关文章:

C#委托事件的实现
1、事件 在C#中事件是一种特殊的委托类型,用于在对象之间提供一种基于观察者模式的通知机制。 1.1、事件的发送方定义了一个委托,委托类型的声明包含了事件的签名,即事件处理器方法的签名。 1.2、事件的订阅者可以通过运算符来注册事件处理器…...

Java策略模式在动态数据验证中的应用
在软件开发中,数据验证是一项至关重要的任务,它确保了数据的完整性和准确性,为后续的业务逻辑处理奠定了坚实的基础。然而,不同的数据来源往往需要不同的验证规则,如何在不破坏代码的整洁性和可维护性的同时࿰…...
)
【Linux】shell基础知识点(updating)
1.输出重定向2.多命令批量执行(; 、&&、 ||)3.脚本不同方式执行的区别(source、bash、sh、./)4.理解环境变量5.export6.引号的使用last.命令相关 1.输出重定向 3种数据流: stdin:标准输入…...

Python基础练习•二
# ## Python编程入门作业 # # ### 选择题 # 1. 假设等号右侧变量都已知的情况下,下列哪个语句在Python中是⾮法的?( B ) # A. x y z 1 # B. x (y z 1) # C. x, y y, x # D. x y # 2. 关于Python变量,下列…...

智慧科技照亮水利未来:深入剖析智慧水利解决方案如何助力水利行业实现高效、精准、可持续的管理
目录 一、智慧水利的概念与内涵 二、智慧水利解决方案的核心要素 1. 物联网技术:构建全面感知网络 2. 大数据与云计算:实现数据高效处理与存储 3. GIS与三维可视化:提升决策支持能力 4. 人工智能与机器学习:驱动决策智能化 …...

Vue3学习笔记(n.0)
vue指令之v-for 首先创建自定义组件(practice5.vue): <!--* Author: RealRoad1083425287qq.com* Date: 2024-07-05 21:28:45* LastEditors: Mei* LastEditTime: 2024-07-05 21:35:40* FilePath: \Fighting\new_project_0705\my-vue-app\…...
基于Spring Boot的在线考试系统
您好!我是专注于计算机技术研究的码农小野。如果您对在线考试系统感兴趣或有相关开发需求,欢迎随时联系我。 开发语言:Java 数据库:MySQL 技术:Spring Boot框架,Java技术 工具:Eclipse&…...

Day65 代码随想录打卡|回溯算法篇---组合总和II
题目(leecode T40): 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意:解集不能包含…...

C++ 入门03:函数与作用域
往期回顾: C 入门01:初识 C-CSDN博客C 入门02:控制结构和循环-CSDN博客 一、前言 在前面的文章学习中,我们了解了C语言的基础,包括如何定义变量来存储数据,以及如何利用输入输出流实现程序与用户之间的无缝…...

在Linux/Debian/Ubuntu中出现“Could not get lock /var/lib/dpkg/lock-frontend”问题的解决办法
在Linux/Debian/Ubuntu中出现“Could not get lock /var/lib/dpkg/lock-frontend”问题的解决办法 在使用 apt 或 apt-get 进行软件包管理时,有时会遇到以下错误提示: Could not get lock /var/lib/dpkg/lock-frontend - open (11: Resource temporari…...

odoo中的钩子 Hooks
钩子 钩子(Hooks)是一种在特定时间点或特定事件发生时执行自定义代码的机制。它们允许开发者在不修改核心代码的情况下,为Odoo添加自定义功能或扩展现有功能。以下是关于Odoo钩子的一些关键点和常见用法: 一、钩子的类型 pre_i…...

05.C1W4.Machine Translation and Document Search
往期文章请点这里 目录 OverviewWhat you’ll be able to do!Learning Objectives Transforming word vectorsOverview of TranslationTransforming vectors Align word vectorsSolving for RFrobenius normFrobenius norm squaredGradient K nearest neighborsFinding the tr…...
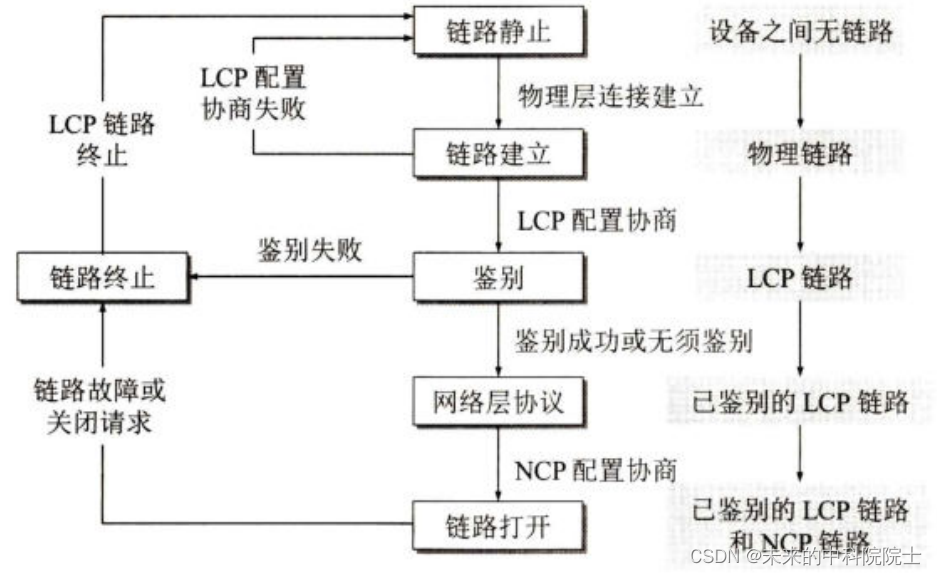
计算机网络——数据链路层(点对点协议PPP)
点对点协议PPP的概述 对于点对点的链路,目前使用得最广泛的数据链路层协议是点对点协议 PPP (Point-to-Point Protocol)。 它主要应用于两个场景: 用户计算机与ISP之间的链路层协议就是点对点协议 PPP,1999年公布了回以在以太网上运行的PPP协…...

信息安全概述
名词解释 大数据:指的是所涉及的资料量规模巨大到无法透过主流软件工具,在合理时间内达到撷取、管理、处理、并整理成为帮助企业经营决策更积极目的的资讯。 云计算:是指通过网络提供计算资源(如服务器、存储、数据库、软件开发…...

UE5.3-基础蓝图类整理一
常用蓝图类整理: 1、获取当前关卡名:Get Current LevelName 2、通过关卡名打开关卡:Open Level(by name) 3、碰撞检测事件:Event ActorBeginOverlap 4、获取当前player:Get Player Pawn 5、判断是否相等࿱…...

Python面试题: 如何在 Python 中实现一个线程池?
在 Python 中,实现线程池可以使用内置的 concurrent.futures 模块,该模块提供了一个高层次的接口来管理并发任务。ThreadPoolExecutor 类是实现线程池的主要工具。以下是一些使用示例,展示如何在 Python 中实现和使用线程池: 1. …...

☺初识c++(语法篇)☺
目录 一命名空间(namespace): 二cout与cin简述: 三缺省参数: 四函数重载: 五引用: 六内联函数: 七c中的nullptr简述: 一命名空间(namespace)࿱…...

process.env 管理 Vue 项目的环境变量(Vue项目中环境变量的配置及调用)
简述:在构建 Vue 应用时,管理配置是开发中的一个重要部分。不同的环境(如开发、测试和生产)往往需要不同的配置,例如 API、 基础 URL、第三方服务的密钥等。使用环境变量可以帮助我们更好地管理这些配置。这里将介绍如…...
)
算法工程师第六天(● 454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和 ● 总结 )
参考文献 代码随想录 一、四数相加 II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1&#…...

笔记:Newtonsoft.Json 自定义一个根据typeconverter转换的JsonConverter
在 Newtonsoft.Json 中创建一个根据 TypeConverter 转换的 JsonConverter 允许你在序列化和反序列化过程中利用 .NET 的 TypeConverter 机制。这种方式特别有用,当你想要为不直接支持 JSON 序列化的类型提供自定义的序列化逻辑时,比如第三方库中的类型或…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
