AFT:Attention Free Transformer论文笔记
原文链接
2105.14103 (arxiv.org)
原文翻译
Abstract
我们介绍了 Attention Free Transformer (AFT),这是 Transformer [1] 的有效变体,它消除了点积自注意力的需要。在 AFT 层,键key和值value首先与一组学习的位置偏差position biases相结合,其结果以元素方式与查询相乘。这种新操作的内存复杂度为线性 w.r.t。上下文大小和特征维度,使其与大输入和模型大小兼容。我们还引入了 AFT-local 和 AFT-conv,这是两个模型变体,它利用了局部性和空间权重共享的思想,同时保持全局连通性。我们在两个自回归建模任务(CIFAR10 和 Enwik8)以及图像识别任务(ImageNet-1K 分类)上进行了广泛的实验。我们表明 AFT 在所有基准测试中都表现出具有竞争力的性能,同时提供了出色的效率。
1 Introduction
以Transformers[1]为代表的自注意机制推动了各种机器学习问题的发展,包括语言理解[2,3]和计算机视觉应用[4 - 6]。与卷积神经网络(cnn)或循环神经网络(rnn)等经典模型架构不同,变形金刚可以在序列中的每对元素之间进行直接交互,这使得它们在捕获长期依赖关系方面特别强大。
然而,变压器需要很高的计算成本。这一挑战的原因是需要执行具有二次时间和空间复杂性的注意力操作,这涉及上下文大小。这使得transformer难以扩展到具有大上下文大小的输入。最近的许多工作都致力于解决transformer的可伸缩性问题[7 -13]。这里的共同思想是近似全注意力操作,使用的技术包括稀疏性、局域敏感散列、低秩分解、核近似等。
在本文中,我们提出了一个不使用或近似标准点积注意力的计算模块。因此,我们将我们的模型命名为不使用注意力的Transformer (AFT)。与点积注意力类似,AFT 由查询、键和值 (Q, K, V) 三个量的交互组成。不同之处在于,在 AFT 中,键和值(上下文)首先与一组可学习的位置偏执相结合然后使用元素乘法将查询与缩减的上下文相结合。有关说明,请参见图 2。
AFT 保留了在上下文中任意两个点之间的直接交互,这是点积注意力的主要优势。事实上,AFT 可以解释为执行注意力,其中注意力头的数量与模型特征维度相同,而注意力图不需要显式计算(详见第 3.1 节)。这导致内存复杂度线性 w.r.t。输入和模型大小。
Q、K、V 的重新排列计算排序在最近的“线性化注意力”工作中也被发现 [11, 13 –15]。不同之处在于 AFT 以元素方式组合 k 和 v,而所有线性注意力论文都依赖于矩阵点积。后一种方法导致复杂度与模型特征维度的二次方,这对大型模型大小不友好。有关 AFT 与其他变体相比的复杂性分析,请参见表 1。
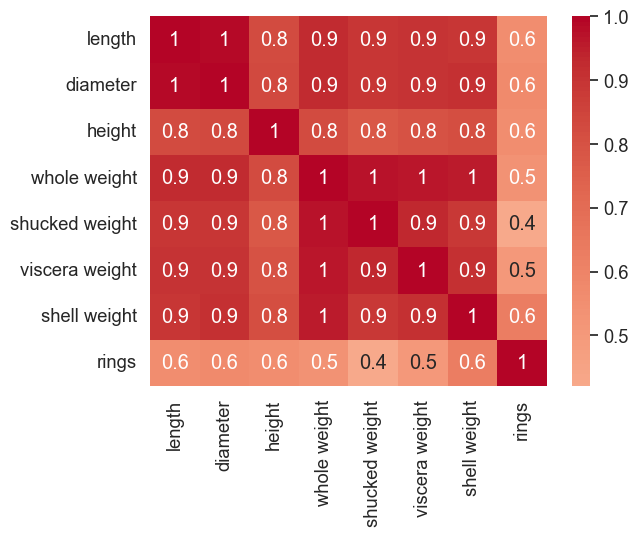
根据经验,我们观察到经过训练的 Transformer 往往表现出广泛的局部模式(见图 1)。这促使我们提出了两种 AFT 变体:AFT-local 和 AFT-conv。在 AFT-local 中,学习到的位置偏差被限制在局部区域,同时保持全局连接。AFT-conv 通过施加空间权重共享进一步扩展了这种设计,有效地使其成为具有全局感受野的 CNN 变体。我们表明,局部性约束不仅提供了更好的参数和计算效率,而且大大提高了模型在所有任务中的表现。
我们在图像自回归建模、字符级语言建模和图像分类任务上使用 AFT 进行了实验。我们表明,AFT 提供了具有竞争力的性能,通常匹配或击败标准 Transformer 和其他变体(的准确度),同时提供了出色的效率。我们还对 AFT 的几种设计选择进行了广泛的消融研究,并讨论了它的独特属性,例如与 Transformer的兼容性、稀疏性和输入大小的可变性。
2 Multi-Head Attention
Transformers 的核心是多头注意力 (MHA) 操作。在自注意模式下,给定一个输入序列 X ∈ R^T ×d 和头部的数量 h,MHA 对每个头部 i 执行缩放的点积注意力,定义为:

其中 W Q i ∈ R^d×dk , W K i ∈ R^d×dk , W V i ∈ R^d×dv 是头部 i 的线性变换,σ 是默认设置为 sof tmax 函数的非线性(应用于矩阵的每一行)。dk, dv 分别是键和值的维度。MHA 将 h 个注意力头的输出沿通道维度拼接起来,得到特征维度 hdv。除非另有说明,我们假设dk=dv和h=d/dk。这意味着查询、键和值在每个头内都是相同的维度,输出维度与输入的维度匹配。
3 Methodology
3.1 Attention Free Transformer
我们现在定义 Attention free Transformer (AFT),它是 MHA 的插件替换,而不需要更改 Transformer 的其他架构方面。给定输入 X,AFT 首先将它们线性变换为 Q = XW^Q, K=XW^K,V =XW^V ,然后进行以下操作 2:

其中 是元素乘积; σq 是应用于query的非线性,默认为 sigmoid; w ∈ RT ×T 是学习的成对位置偏差(参见图 2 的说明)。

简而言之,对于每个目标位置t, AFT执行value的加权平均值,其结果与query进行元素间乘法相结合。具体来说,相结合的权重只是由键和一组学习得到的成对位置偏差组成。这提供了不需要计算和存储昂贵的注意力矩阵的直接优势,同时像MHA那样维护查询和值之间的全局交互。为了进一步了解AFT与MHA的关系,我们可以将方程2改写为:

这里我们使用上标 i 来索引矩阵的特征维度; <·, · >; 表示向量的点积。在这个重新排列的形式中,我们能够再次根据注意力来表达 AFT。具体来说,对于每个位置,我们对每个维度都有一个注意力向量 ai t ∈ RT,由 Q、K、w 组成。换句话说,AFT 可以解释为执行隐式注意力,头部数量与特征维度一样多,其中注意力矩阵采用分解形式。
下略
相关文章:

AFT:Attention Free Transformer论文笔记
原文链接 2105.14103 (arxiv.org) 原文翻译 Abstract 我们介绍了 Attention Free Transformer (AFT),这是 Transformer [1] 的有效变体,它消除了点积自注意力的需要。在 AFT 层,键key和值value首先与一组学习的位置偏差position biases相结…...

Linux grep技巧 结合awk查询
目录 一. 前提1.1 数据准备1.2 数据说明 二. 查询2.1 统计每个加盟店搜索的次数 一. 前提 1.1 数据准备 ⏹file1.log 140 2024/07/08 12:35:01.547 c1server2 5485 [ERROR] SPLREQUEST seqNo11459,eventControllerPMT.payinfoforprc.test.search,oldest_data_search2 110 20…...

关于Qt模型插入最后一行数据中存在未填满的项,点击导致崩溃的解决办法
在使用Qt模型视图框架的时候,你可能会遇见这种情况:给QTableView设置设置模型的时候,网模型里面插入数据,因为数据是一行一行插入的,即要使用model的appandRow函数,但有时候最后一行数据没有填满一行&#…...
Interpretability 与 Explainability 机器学习
「AI秘籍」系列课程: 人工智能应用数学基础人工智能Python基础人工智能基础核心知识人工智能BI核心知识人工智能CV核心知识 Interpretability 模型和 Explainability 模型之间的区别以及为什么它可能不那么重要 当你第一次深入可解释机器学习领域时,你会…...

Vue3项目如何使用npm link本地测试组件库
一、组件库操作 1、在组件库项目中先运行npm run lib,其效果如下 2、在组件库项目中在运行npm link,其效果如下 会创建一个全局的软连接指向本地的组件库 二、Vue3项目使用 1、在项目中运行 npm link 组件名称(即:组件库packag…...
后端之路——阿里云OSS云存储
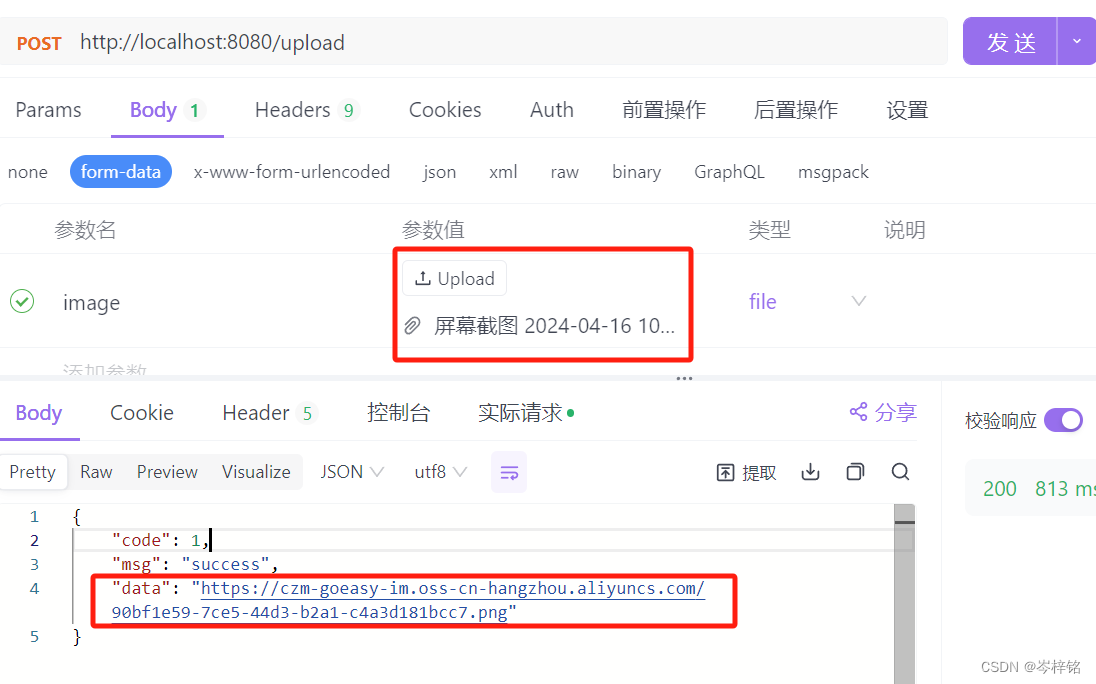
一、何为阿里云OSS 全名叫“阿里云对象存储OSS”,就是云存储,前端发文件到服务器,服务器不用再存到本地磁盘,可以直接传给“阿里云OSS”,存在网上。 二、怎么用 大体逻辑: 细分的话就是: 1、准…...

大模型/NLP/算法面试题总结2——transformer流程//多头//clip//对比学习//对比学习损失函数
用语言介绍一下Transformer的整体流程 1. 输入嵌入(Input Embedding) 输入序列(如句子中的单词)首先通过嵌入层转化为高维度的向量表示。嵌入层的输出是一个矩阵,每一行对应一个输入单词的嵌入向量。 2. 位置编码&…...

【atcoder】习题——位元枚举
题意:求i&M的popcount的和,i属于0……N 主要思路还是变加为乘。 举个例子N22,即10110 假设M的第3位是1,分析N中: 00110 00111 00100 00101 发现其实等价于 0010 0011 0000 0001 也就是左边第4位和第5…...
世界人工智能大会 | 江行智能大模型解决方案入选“AI赋能新型工业化创新应用优秀案例”
日前,2024世界人工智能大会暨人工智能全球治理高级别会议在上海启幕。本次大会主题为“以共商促共享,以善治促善智”,汇聚了上千位全球科技、产业界领军人物,共同探讨大模型、数据、新型工业化等人工智能深度发展时代下的热点话题…...

css浮动及清除浮动副作用的三种解决方法
css浮动及清除浮动副作用的三种解决方法 文章目录 css浮动及清除浮动副作用的三种解决方法一、浮动定义二、浮动元素设置三、清除浮动副作用方法一四、清除浮动副作用方法二五、清除浮动副作用方法三 一、浮动定义 浮动(Float)是CSS中一种布局技术&…...

图像类别生成数字标签
类别 COCO 2017数据集分类标签。coco2017数据集下载。 cls [background, person, bicycle, car, motorcycle, airplane, bus,train, truck, boat, traffic light, fire hydrant,stop sign, parking meter, bench, bird, cat, dog,horse, sheep, cow, elephant, bear, zebra,…...

【Python】已解决:SyntaxError: invalid character in identifier
文章目录 一、分析问题背景二、可能出错的原因三、错误代码示例四、正确代码示例五、注意事项 已解决:SyntaxError: invalid character in identifier 一、分析问题背景 在Python编程中,SyntaxError: invalid character in identifier是一个常见的编译…...

RDNet实战:使用RDNet实现图像分类任务(一)
论文提出的模型主要基于对传统DenseNet架构的改进和复兴,通过一系列创新设计,旨在提升模型性能并优化其计算效率,提出了RDNet模型。该模型的主要特点和改进点: 1. 强调并优化连接操作(Concatenation) 论文…...

Java小白入门到实战应用教程-介绍篇
writer:eleven 介绍 编程语言介绍 编程语言按照抽象层次和硬件交互的方式划分为低级编程语言和高级编程语言。 低级编程语言更接近计算机硬件层面,通常具有执行效率高的特点,但是由于注重计算机底层交互,所以编程难度相对较大。 高级编程…...

python脚本“文档”撰写——“诱骗”ai撰写“火火的动态”python“自动”脚本文档
“火火的动态”python“自动”脚本文档,又从ai学习搭子那儿“套”来,可谓良心质量👍👍。 (笔记模板由python脚本于2024年07月07日 15:15:33创建,本篇笔记适合喜欢钻研python和页面源码的coder翻阅) 【学习的细节是欢悦…...

若依 / ruoyi-ui:执行yarn dev 报错 esnext.set.difference.v2.js in ./src/utils/index.js
一、报错信息 These dependencies were not found: * core-js/modules/esnext.set.difference.v2.js in ./src/utils/index.js * core-js/modules/esnext.set.intersection.v2.js in ./src/utils/index.js * core-js/modules/esnext.set.is-disjoint-from.v2.js in ./src/utils…...

移动端Vant-list的二次封装,查询参数重置
Vant-list的二次封装 场景:在写项目需求的时候,移动端有用到vant-list组件。后续需求更新说要对列表数据页加搜索和筛选的功能。发现每次筛选完得在页面内手动重置一次查询参数。不方便,所以封了一层。 二次封装代码 <template><…...

SMU Summer 2024 Contest Round 2
[ABC357C] Sierpinski carpet - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路:通过因为图形的生成过程是完全一样的。可以通过递归,不断分形。函数process(x,y,k)定义为以坐标(x,y)为左上角,填充sqrt3(k)级的地毯。 int n; int c[800][800]; 默认全为…...

Qt:11.输入类控件(QLineEdit-单行文本输入控件、QTextEdit-多行文本输入控件、QComboBox-下拉列表的控件)
一、QLineEdit-单行文本输入控件: 1.1QLineEdit介绍: QLineEdit 是 Qt 库中的一个单行文本输入控件,不能换行。允许用户输入和编辑单行文本。 1.2属性介绍: inputMask 设置输入掩码,以限定输入格式。setInputMask(con…...

Qt 音频编程实战项目
一Qt 音频基础知识 QT multimediaQMediaPlayer 类:媒体播放器,主要用于播放歌曲、网络收音 机等功能。QMediaPlaylist 类:专用于播放媒体内容的列表。 二 音频项目实战程序 //版本5.12.8 .proQT core gui QT multimedia greate…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
