每日刷题(二分查找,匈牙利算法,逆序对)
目录
1.Saruman's Army
2.Catch That Cow
3.Drying
4.P3386 【模板】二分图最大匹配
5. Swap Dilemma
1.Saruman's Army
3069 -- Saruman's Army (poj.org)


这道题就是要求我们在给的的位置放入 palantir,每个 palantir有R大小的射程范围,要求求出最少需要安装多少个 palantir,才能将让所有的军队在射程范围内。
思路:
先将军队的位置排序,为二分做准备。
先枚举第一个位置,二分找到小于等于这个位置+R的位置,在此位置安装一个 palantir。
再从这个位置开始重复上述操作。直到索引i>n。
#include<iostream>
#include<algorithm>
#define ll long long
#define TEST int T;cin>>T;while(T--)
#define lowbit(x) x&(-x)
using namespace std;
const int N = 1500;
const int M = 1e9 + 2;
int base1 = 131, base2 = 13311;
ll a[N];
void solve()
{ll n,k;while(cin>>k>>n){if(k==-1) break;for(int i=1;i<=n;i++) cin>>a[i];ll ans=0;sort(a+1,a+1+n);int i=1;while(i<=n){ans++;//找安装的位置int pos=upper_bound(a+1,a+1+n,a[i]+k)-a-1;pos=upper_bound(a+1,a+1+n,a[pos]+k)-a;i=pos;}cout<<ans<<"\n";}
}
int main()
{solve();return 0;
}2.Catch That Cow
3278 -- Catch That Cow (poj.org)


给出我们起点和终点,要求我们求出从起点到终点最少需要几个操作。
操作1:当前位置+1
操作2:当前位置-1
操作3:传送到当前位置*2的位置
思路:
用bfs算法去搜索答案。注意不能乱搜索:
当当前位置大于终点位置,不能入队操作1和3
当当前位置小于0,不能入队操作3
当当前位置大于终点位置,才能入队操作2
#include<iostream>
#include<algorithm>
#include<queue>
#define ll long long
#define TEST int T;cin>>T;while(T--)
#define lowbit(x) x&(-x)
using namespace std;
const int N = 1500;
const int M = 200010;
int base1 = 131, base2 = 13311;
ll a[N],v[M];
struct node
{ll v,st;
};
void solve()
{ll n,k;cin>>n>>k;queue<node>q;node start,nextt;start.st=0,start.v=n;q.push(start);while(!q.empty()){node t=q.front();q.pop();if(t.v==k){cout<<t.st<<"\n";return;}if(t.v>0&&!v[t.v-1])nextt.v=t.v-1,nextt.st=t.st+1,q.push(nextt),v[t.v-1]=1;if(t.v<k&&!v[t.v+1])nextt.v=t.v+1,nextt.st=t.st+1,q.push(nextt),v[t.v+1]=1;if(t.v>0&&t.v<k&&!v[2*t.v])nextt.v=t.v*2,nextt.st=t.st+1,q.push(nextt),v[2*t.v]=1;}
}
int main()
{solve();return 0;
}3.Drying
3104 -- Drying (poj.org)


要求求出全部衣物都干的最短时间。
二分答案去求解,L为1,R为最湿的衣服的湿润度。
如何判断mid可行?
对衣服的湿润度排序,找到大于mid的衣服,将它减去,再除以烘干片每分钟可以减少的湿润度,向上取整。最后这个值要是小于mid,则这个值可行。
#include<iostream>
#include<algorithm>
#include<queue>
#include<math.h>
#define ll long long
#define TEST int T;cin>>T;while(T--)
#define lowbit(x) x&(-x)
using namespace std;
const int N = 150000;
const int M = 200010;
int base1 = 131, base2 = 13311;
ll n, k, a[N];
bool check(ll x) {ll ans = x;int pos = upper_bound(a + 1, a + 1 + n, x) - a;for (int i = pos; i <= n; i++) {ans -= (a[i] - x + k - 2) / (k - 1);if (ans < 0) return false;}return true;
}
void solve() {scanf("%lld", &n);for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);scanf("%lld", &k);sort(a + 1, a + 1 + n);if (k == 1) {cout << a[n] << "\n";return ;}ll l = 1, r = a[n], mid;while (l < r) {mid = l + r >> 1;if (check(mid)) { //这段时间可以烘干,再试试更短的时间r = mid;} else {l = mid + 1;}}cout << r << "\n";
}
int main() {solve();return 0;
}4.P3386 【模板】二分图最大匹配
P3386 【模板】二分图最大匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

匈牙利算法的板子题。
#include<iostream>
#include<algorithm>
#include<queue>
#include<math.h>
#include<cstring>
#define ll long long
#define TEST int T;cin>>T;while(T--)
#define lowbit(x) x&(-x)
using namespace std;
const int N = 100010;
const int M = 16000101;
int base1 = 131, base2 = 13311;
ll colour[N], head[N];
struct Node {int u, v, net;
} e[N << 2];
ll n, m, cnt = 0;
ll v[N];
vector<vector<ll> >f;
bool dfs(int x, int co) {if (v[x] == co) return false;v[x] = co;for (auto k : f[x]) {if (!head[k] || dfs(head[k], co)) {head[k] = x;return true;}}return false;
}
void solve() {cin >> n >> m >> cnt;f.resize(n + m + 1);for (int u, v; cnt; cnt--) {cin >> u >> v;f[u].push_back(v);}ll ans = 0;for (int i = 1; i <= n; i++) {if (dfs(i, i)) ans++;}cout << ans << "\n";
}
int main() {solve();return 0;
}5. Swap Dilemma
Problem - D - Codeforces


先将两个数组排序,再判断这两个数组是否相同,相同再进行下一步,反之直接输出NO。
求逆序对,分别讨论两个逆序对的奇偶性,奇偶性相同则输出YES,反之输出NO。
#include<iostream>
#include<algorithm>
#include<queue>
#include<math.h>
#include<cstring>
#include<map>
#define ll long long
#define TEST int T;cin>>T;while(T--)
#define lowbit(x) x&(-x)
using namespace std;
const int N = 100010;
const int M = 200010;
int base1 = 131, base2 = 13311;
ll n, rak1[N], rak2[N];
struct Node {ll v, id;
} e1[N], e2[N];
map<ll,ll>f1,f2;
bool cmp(Node a, Node b) {if (a.v == b.v) return a.id < b.id;return a.v < b.v;
}
void add1(int pos) {for (int i = pos; i <= n; i += lowbit(i)) f1[i]++;
}
void add2(int pos) {for (int i = pos; i <= n; i += lowbit(i)) f2[i]++;
}
ll ask1(int pos) {ll ans = 0;for (int i = pos; i >= 1; i -= lowbit(i)) ans += f1[i];return ans;
}
ll ask2(int pos) {ll ans = 0;for (int i = pos; i >= 1; i -= lowbit(i)) ans += f2[i];return ans;
}
void solve() {scanf("%lld", &n);f1.clear();f2.clear();for (int i = 1; i <= n; i++) {scanf("%lld", &e1[i].v), e1[i].id = i;}for (int i = 1; i <= n; i++) {scanf("%lld", &e2[i].v), e2[i].id = i;}sort(e1 + 1, e1 + 1 + n, cmp);sort(e2 + 1, e2 + 1 + n, cmp);for (int i = 1; i <= n; i++) {if (e1[i].v != e2[i].v) {cout << "NO\n";return;}rak1[e1[i].id] = i;rak2[e2[i].id] = i;}ll ans1 = 0, ans2 = 0;for (int i = 1; i <= n; i++) {int pos1, pos2;pos1 = rak1[i];pos2 = rak2[i];ans1 += ask1(n) - ask1(pos1);ans2 += ask2(n) - ask2(pos2);add1(pos1);add2(pos2);}if (abs(ans1 - ans2) % 2 != 0) {cout << "NO\n";} else {cout << "YES\n";}
}
int main() {TESTsolve();return 0;
}相关文章:

每日刷题(二分查找,匈牙利算法,逆序对)
目录 1.Sarumans Army 2.Catch That Cow 3.Drying 4.P3386 【模板】二分图最大匹配 5. Swap Dilemma 1.Sarumans Army 3069 -- Sarumans Army (poj.org) 这道题就是要求我们在给的的位置放入 palantir,每个 palantir有R大小的射程范围,要求求出最少…...

LLM应用构建前的非结构化数据处理(三)文档表格的提取
1.学习内容 本节次学习内容来自于吴恩达老师的Preprocessing Unstructured Data for LLM Applications课程,因涉及到非结构化数据的相关处理,遂做学习整理。 本节主要学习pdf中的表格数据处理 2.环境准备 和之前一样,可以参考LLM应用构建前…...
如何从数码相机恢复已删除的照片
照片恢复是恢复已删除照片的最佳工具,它带有恢复 RAW 照片的选项。在本文中,我们将解释如何恢复已删除的照片。 不仅对于专业摄影师,对于像我们这样喜欢捕捉回忆的人来说,瞬间相机都是重要的数码设备。遗憾的是,就像智…...
)
设计模式使用场景实现示例及优缺点(创建型模式——单例模式、建造者模式、原型模式)
创建型模式 单例模式(Singleton Pattern) 单例模式(Singleton Pattern)在Java中的使用场景与在其他编程语言中类似,其主要目的是确保一个类只有一个实例,并提供一个全局的访问点。以下是单例模式的一些常…...

LAMP万字详解(概念、构建步骤)
目录 LAMP Apache 起源 主要特点 软件版本 编译安装httpd服务器 编译安装的优点 操作步骤 准备工作 编译 安装 优化执行路径 添加服务 守护进程 配置httpd 查看 Web 站点的访问情况 虚拟主机 类型 部署基于域名的虚拟主机 为虚拟主机提供域名解析ÿ…...

金南瓜科技SECS/GEM:引领智能制造新潮流
引言 在当今快速发展的半导体行业中,智能制造和自动化生产已成为提升效率和降低成本的关键。金南瓜科技凭借其先进的SECS/GEM解决方案,正成为这一变革的先锋。 SECS/GEM:智能制造的核心 SECS/GEM(SEMI Equipment Communications …...
)
昇思训练营打卡第二十一天(DCGAN生成漫画头像)
DCGAN,即深度卷积生成对抗网络(Deep Convolutional Generative Adversarial Network),是一种深度学习模型,由Ian Goodfellow等人在2014年提出。DCGAN在生成对抗网络(GAN)的基础上,引…...

东方通Tongweb发布vue前端
一、前端包中添加文件 1、解压vue打包文件 以dist.zip为例,解压之后得到dist文件夹,进入dist文件夹,新建WEB-INF文件夹,进入WEB-INF文件夹,新建web.xml文件, 打开web.xml文件,输入以下内容 …...
)
spring xml实现bean对象(仅供自己参考)
对于spring xml来实现bean 具体代码: <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaL…...

MiniGPT-Med 通用医学视觉大模型:生成医学报告 + 视觉问答 + 医学疾病识别
MiniGPT-Med 通用医学视觉大模型:生成医学报告 视觉问答 医学疾病识别 提出背景解法拆解 论文:https://arxiv.org/pdf/2407.04106 代码:https://github.com/Vision-CAIR/MiniGPT-Med 提出背景 近年来,人工智能(AI…...

如何判断ip地址在同一个网段:技术解析与实际应用
在网络世界中,IP地址就像每个人的身份证一样,是识别和定位网络设备的关键。然而,仅仅知道IP地址还不足以完全理解其背后的网络结构和通信方式。特别是当我们需要判断两个或多个IP地址是否位于同一网段时,就需要借助子网掩码这一概…...
(传输控制协议))
linux高级编程(TCP)(传输控制协议)
TCP与UDP: TCP: TCP优点: 可靠,稳定 TCP的可靠体现在TCP在传递数据之前,会有三次握手来建立连接,而且在数据传递时,有确认、窗口、重传、拥塞控制机制,在数据传完后,还会断开连接用来节约系统…...

【常见开源库的二次开发】一文学懂CJSON
简介: JSON(JavaScript Object Notation)是一种轻量级的数据交换格式。它基于JavaScript的一个子集,但是JSON是独立于语言的,这意味着尽管JSON是由JavaScript语法衍生出来的,它可以被任何编程语言读取和生成…...

点云下采样有损压缩
转自本人博客:点云下采样有损压缩 点云下采样是通过一定规则对原点云数据进行再采样,减少点云个数,降低点云稀疏程度,减小点云数据大小。 1. 体素下采样(Voxel Down Sample) std::shared_ptr<PointClo…...
转义符号)
AutoHotKey自动热键(六)转义符号
转义符号 符号说明,, (原义的逗号). 注意: 在命令最后一个参数中的逗号不需要转义, 因为程序知道把它们作为原义处理. 对于 MsgBox 所有参数同样如此, 因为它会智能的处理逗号.%% (原义的百分号) (原义的重音符; 即两个连续的转义符产生单个原义字符);; (原义的分号). 注意: 仅…...

第16章 主成分分析:四个案例及课后习题
1.假设 x x x为 m m m 维随机变量,其均值为 μ \mu μ,协方差矩阵为 Σ \Sigma Σ。 考虑由 m m m维随机变量 x x x到 m m m维随机变量 y y y的线性变换 y i α i T x ∑ k 1 m α k i x k , i 1 , 2 , ⋯ , m y _ { i } \alpha _ { i } ^ { T } …...

股票分析系统设计方案大纲与细节
股票分析系统设计方案大纲与细节 一、引言 随着互联网和金融行业的迅猛发展,股票市场已成为重要的投资渠道。投资者在追求财富增值的过程中,对股票市场的分析和预测需求日益增加。因此,设计并实现一套高效、精准的股票分析系统显得尤为重要。本设计方案旨在提出一个基于大…...

.gitmodules文件
.gitmodules文件在Git仓库中的作用 .gitmodules 文件是 Git 版本控制系统中用来跟踪和管理子模块的配置文件。子模块允许你将一个 Git 仓库嵌套在另一个仓库中,这样可以方便地管理多个项目之间的依赖关系。 在 .gitmodules 文件中,通常会记录每个子模块…...

STM32 SPI世界:W25Q64 Flash存储器的硬件与软件集成策略
摘要 在嵌入式系统设计中,选择合适的存储解决方案对于确保数据的安全性和系统的可靠性至关重要。W25Q64 Flash存储器因其高性能和大容量成为STM32微控制器项目中的热门选择。本文将深入探讨STM32与W25Q64 Flash存储器的硬件连接、软件集成以及SPI通信的最佳实践。 …...
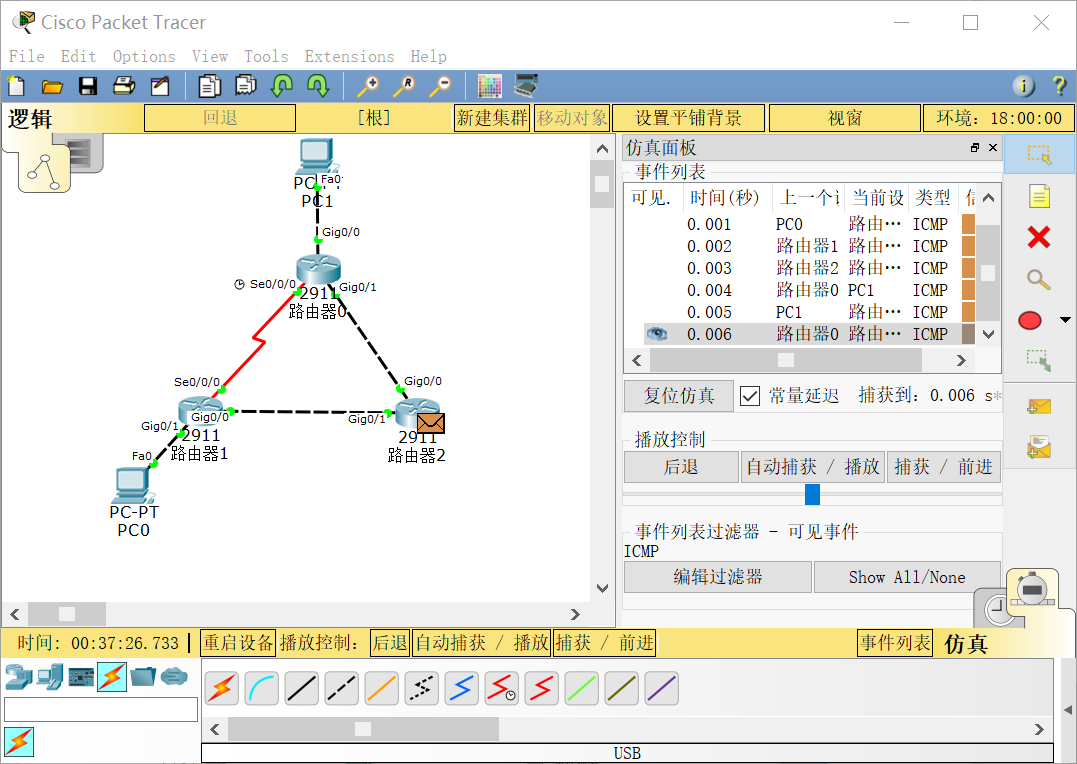
【计算机网络仿真】b站湖科大教书匠思科Packet Tracer——实验17 开放最短路径优先OSPF
一、实验目的 1.验证OSPF协议的作用; 二、实验要求 1.使用Cisco Packet Tracer仿真平台; 2.观看B站湖科大教书匠仿真实验视频,完成对应实验。 三、实验内容 1.构建网络拓扑; 2.验证OSPF协议的作用。 四、实验步骤 1.构建网…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
