redhat7.x 升级openssh至openssh-9.8p1
1.环境准备:
OS系统:redhat 7.4

2.备份配置文件:
cp -rf /etc/ssh /etc/ssh.bak
cp -rf /usr/bin/openssl /usr/bin/openssl.bak
cp -rf /etc/pam.d /etc/pam.d.bak
cp -rf /usr/lib/systemd/system /usr/lib/systemd/system.bak

3.安装GCC编译器
GCC离线安装包如下:
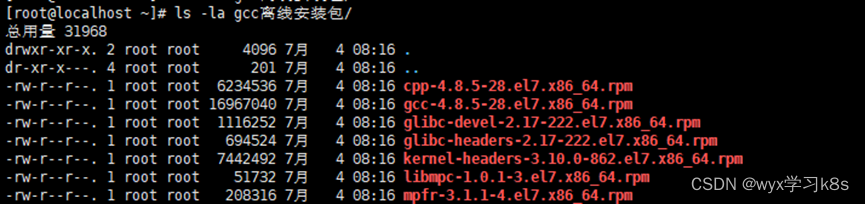
我们可以按照下列顺序依次安装:
rpm -ivh mpfr-3.1.1-4.el7.x86_64.rpm
rpm -ivh libmpc-1.0.1-3.el7.x86_64.rpm
rpm -ivh kernel-headers-3.10.0-862.el7.x86_64.rpm
rpm -ivh glibc-headers-2.17-222.el7.x86_64.rpm
rpm -ivh glibc-devel-2.17-222.el7.x86_64.rpm
rpm -ivh cpp-4.8.5-28.el7.x86_64.rpm
rpm -ivh gcc-4.8.5-28.el7.x86_64.rpm
也可以直接用这一条rpm -ivh *.rpm --nodeps --force安装

安装完成后,用gcc -v验证

4. 编译安装per(安装openssl需要)
安装包为:perl-5.34.0.tar.gz

解压:tar -zxvf perl-5.34.0.tar.gz
cd perl-5.34.0
安装配置:./Configure -des -Dprefix=/usr/local/perl
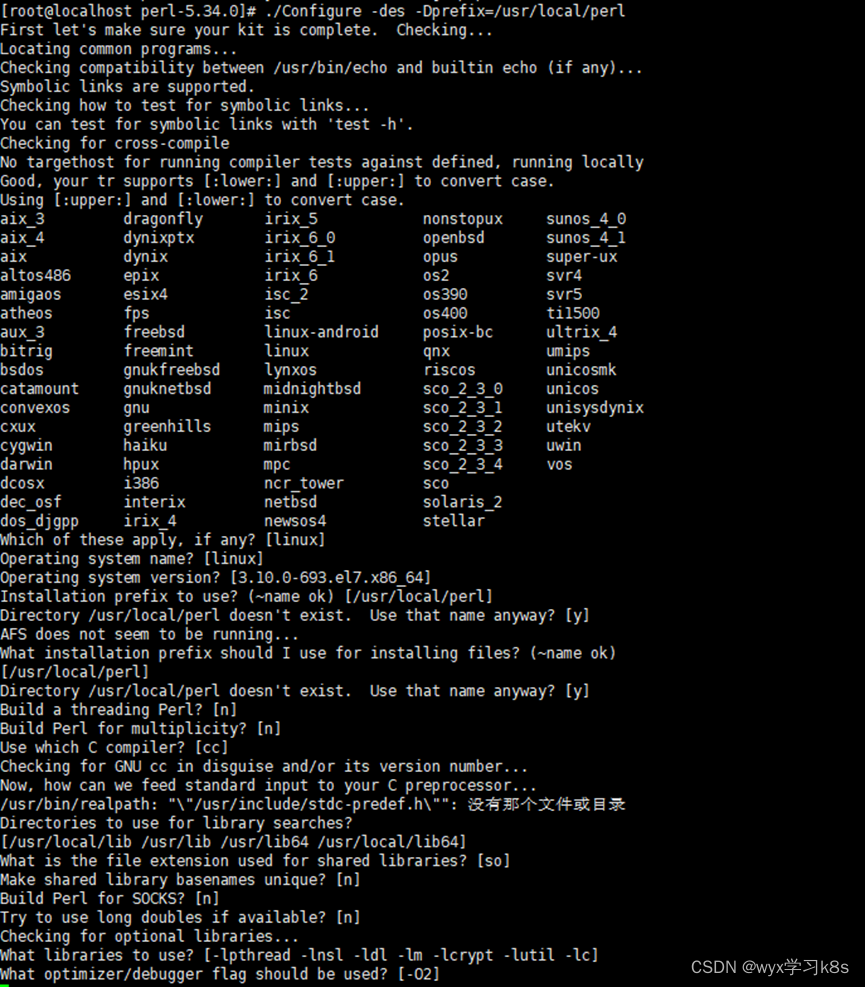
编译安装:make && make test && make install (这一步在make test步骤有点慢,大概15分钟左右)

添加环境变量:
echo "export PERL_HOME=/usr/local/perl" >> /etc/profile
echo "export PATH=\$PERL_HOME/bin:\$PATH" >> /etc/profile
source /etc/profile
版本验证:perl -v
5. 编译升级zlib
安装包为:zlib-1.3.1.tar.gz

解压:tar -zxvf zlib-1.3.1.tar.gz

安装配置:cd zlib-1.3.1 && ./configure --prefix=/usr/local/zlib
编译:make -j 2
测试软件:make test

安装:make install
添加库文件:echo '/usr/local/zlib/lib' >> /etc/ld.so.conf.d/zlib.conf
ldconfig -v

6. 编译升级openssl
安装包为:openssl-1.1.1v.tar.gz

解压:tar -zxvf openssl-1.1.1v.tar.gz
安装配置:cd openssl-1.1.1v && ./config --prefix=/usr/local/openssl -d shared

编译:make -j 2
安装:make install
添加库文件:echo '/usr/local/ssl/lib' >> /etc/ld.so.conf
ldconfig -v |grep ssl
mv /usr/bin/openssl /usr/bin/openssl.bak
ln -s /usr/local/openssl/bin/openssl /usr/bin/openssl
ln -s /usr/local/openssl/lib/libssl.so.1.1 /usr/lib64/libssl.so.1.1
ln -s /usr/local/openssl/lib/libcrypto.so.1.1 /usr/lib64/libcrypto.so.1.1
openssl version
![]()
7. 编译安装openssh
安装包为:openssh-9.8p1.tar.gz

解压安装包:tar -zxvf openssh-9.8p1.tar.gz
卸载旧的sshd服务(切记不能重启或者关掉远程工具):yum remove openssh

配置安装:cd openssh-9.8p1 && ./configure --prefix=/usr/local/openssh --sysconfdir=/etc/ssh --with-pam --with-ssl-dir=/usr/local/openssl/ --with-zlib=/usr/local/zlib
编译以及安装:make -j 4 && make install
cp contrib/redhat/sshd.init /etc/init.d/sshd
ll /etc/init.d/
chkconfig --add sshd
配置文件修改:
echo "X11Forwarding yes" >> /etc/ssh/sshd_config
echo "X11UseLocalhost no" >> /etc/ssh/sshd_config
echo "XAuthLocation /usr/bin/xauth" >> /etc/ssh/sshd_config
echo "UseDNS no" >> /etc/ssh/sshd_config
echo 'PermitRootLogin yes' >> /etc/ssh/sshd_config
echo 'PubkeyAuthentication yes' >> /etc/ssh/sshd_config
echo 'PasswordAuthentication yes' >> /etc/ssh/sshd_config
将新的配置复制到指定目录:
cp -rf /usr/local/openssh/sbin/sshd /usr/sbin/sshd
cp -rf /usr/local/openssh/bin/ssh /usr/bin/ssh
cp -rf /usr/local/openssh/bin/ssh-keygen /usr/bin/ssh-keygen
版本验证:ssh -V

sshd服务重启:systemctl restart sshd
systemctl status sshd
reboot重启服务器后能再次连接,查看服务正常systemctl status sshd

碰到的报错:在make install 安装openssh时碰到文件权限太大,需要用下面命令修改文件权限后再次make install

[root@localhost openssh-9.8p1]# chmod 600 /etc/ssh/ssh_host_rsa_key
[root@localhost openssh-9.8p1]# chmod 600 /etc/ssh/ssh_host_ecdsa_key
[root@localhost openssh-9.8p1]# chmod 600 /etc/ssh/ssh_host_ed25519_key
注意:附件脚本升级的openssh是带pam模块的,之前测试是没有带pam模块,pam-devel rpm包时直接放在gcc里面一同安装了。
相关文章:

redhat7.x 升级openssh至openssh-9.8p1
1.环境准备: OS系统:redhat 7.4 2.备份配置文件: cp -rf /etc/ssh /etc/ssh.bak cp -rf /usr/bin/openssl /usr/bin/openssl.bak cp -rf /etc/pam.d /etc/pam.d.bak cp -rf /usr/lib/systemd/system /usr/lib/systemd/system.bak 3.安装…...

Spring Cloud Eureka
引入:远程调用时,url是写死的 String url "http://127.0.0.1:9090/product/" orderInfo.getProductId(); 解决思路: 比如(医院,学校等)机构的电话号码发生变化,就需要通知各个使⽤…...

threejs
1.场景清空,释放内容 // 假设你已经有一个Three.js的场景对象scene// 函数:清空场景中的所有对象 function clearScene(scene) {while(scene.children.length > 0){const object scene.children[0];if(object.isMesh) {// 如果有几何体和材质&#…...

将pytorch 模型封装为c++ api 例子
在 PyTorch 中,通常使用 Python 来定义和训练模型,但是可以将训练好的模型导出为 TorchScript,然后在 C 中加载和使用。以下是一个详细的过程,展示了如何将 PyTorch 模型封装成 C API: 步骤 1: 定义和训练模型&#x…...

珠宝迷你秤方案
珠宝迷你秤作为一种便携式电子称重设备,因其小巧、便携、精度高等特点,广泛应用于各种需要精确称重的场景。可能这个目前在国内使用的人比较少,但在西方国家珠宝迷你秤却是可以用来送礼的物品。因为珠宝迷你秤的外观跟手机外观大多相似&#…...

边缘概率密度、条件概率密度、边缘分布函数、联合分布函数关系
目录 二维随机变量及其分布离散型随机变量连续型随机变量边缘分布边缘概率密度举例边缘概率密度 条件概率密度边缘概率密度与条件概率密度的区别边缘概率密度条件概率密度举个具体例子 参考资料 二维随机变量及其分布 离散型随机变量 把所有的概率,都理解成不同质量…...

软件架构之系统分析与设计方法(2)
软件架构之系统分析与设计方法(2) 8.4 面向对象的分析与设计8.4.1 面向对象的基本概念8.4.2 面向对象分析8.4.3 统一建模语言 8.5 用户界面设计8.5.1 用户界面设计的原则8.5.2 用户界面设计过程 8.6 工作流设计8.6.1 工作流设计概述8.6.2 工作流管理系统 8.7 简单分…...

AD确定板子形状
方法1 修改栅格步进值,手动绘制 https://cnblogs.com/fqhy/p/13768031.html 方法2 器件摆放确定板子形状 https://blog.csdn.net/Mark_md/article/details/116445961...

CSS【详解】边框 border,边框-圆角 border-radius,边框-填充 border-image,轮廓 outline
边框 border border 是以下三种边框样式的简写: border-width 边框宽度 —— 数值 px(像素),thin(细),medium(中等),thick(粗)border-style 边框线型 —— none【默认值…...

Error: EBUSY: resource busy or locked, rmdir...npm install执行报错
Error: EBUSY: resource busy or locked, rmdir...npm install执行报错 你一个文件夹目录开了两个cmd命令行(或者powershell),关掉一个就好了。...

Hot100-排序
1.快排 215. 数组中的第K个最大元素 - 力扣(LeetCode) (1)第k大的元素在排序数组中的位置是nums.length - k。 假设我们有一个数组nums [3, 2, 1, 5, 6, 4],并且我们想找到第2大的元素。 步骤 1:排序数…...
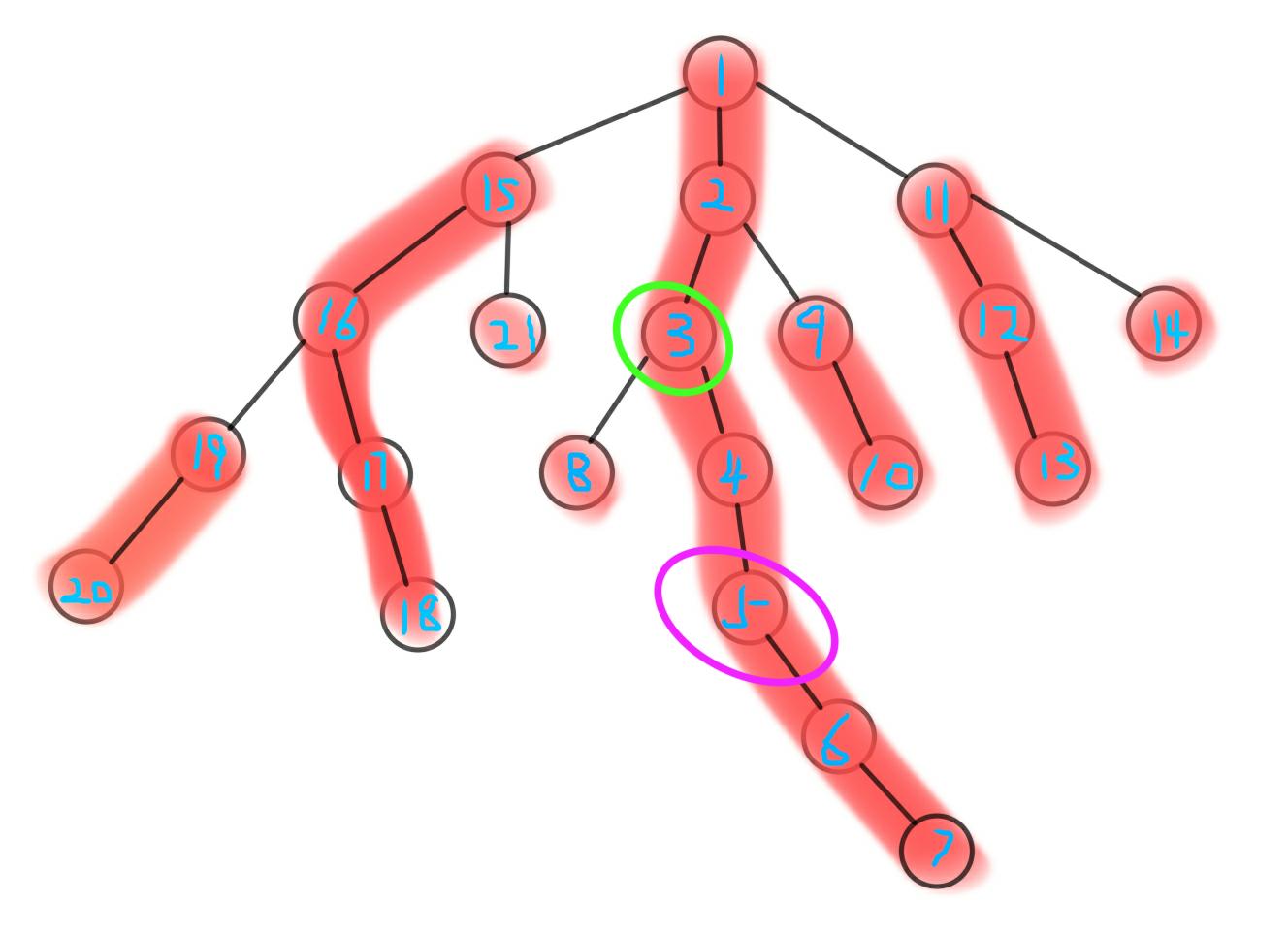
树链剖分相关
树链剖分这玩意儿还挺重要的,是解决静态树问题的一个很好的工具~ 这里主要介绍一下做题时经常遇到的两个操作: 1.在线求LCA int LCA(int x,int y){while(top[x]!top[y])if(dep[top[x]]>dep[top[y]]) xfa[top[x]];else yfa[top[y]];return dep[x]&l…...

如何将Grammarly内嵌到word中(超简单!)
1、下载 安装包下载链接见文章结尾 官网的grammarly好像只能作为单独软件使用,无法内嵌到word中🧐🧐🧐 2、双击安装包(安装之前把Office文件都关掉) 3、安装完成,在桌面新建个word文件并打开 注…...

OTG -- 用于FPGA的ULPI接口芯片USB3320讲解(续)
目录 1 背景 2 USB3320在FPGA上的应用 1 背景 最近使用FPGA驱动USB PHY实现高速USB功能,为了方便,购买了一块微雪的USB3300子板,发现怎么都枚举不了,使用逻辑分析仪抓取波形,和STM32F407USB3300波形进行对比…...

了解劳动准备差距:人力资源专业人员的战略
劳动准备差距是一个紧迫的问题,在全球人事部门回应,谈论未开发的潜力和错过的机会。想象一下,人才和需求之间的悬崖之间有一座桥,这促使雇主思考:我们是否为员工提供了足够的设备来应对未来的考验? 这种不…...

SAP PS学习笔记02 - 网络,活动,PS文本,PS文书(凭证),里程碑
上一章讲了PS 的概要,以及创建Project,创建WBS。 SAP PS学习笔记01 - PS概述,创建Project和WBS-CSDN博客 本章继续讲PS的后续内容。包括下面的概念和基本操作,以及一些Customize: - 网络(Network…...

Github 2024-07-07php开源项目日报 Top9
根据Github Trendings的统计,今日(2024-07-07统计)共有9个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量PHP项目9Blade项目2JavaScript项目1Laravel:表达力和优雅的 Web 应用程序框架 创建周期:4631 天开发语言:PHP, BladeStar数量:75969 个Fork数…...
第二十六天 | 452. 用最少数量的箭引爆气球、435. 无重叠区间、763. 划分字母区间)
算法训练(leetcode)第二十六天 | 452. 用最少数量的箭引爆气球、435. 无重叠区间、763. 划分字母区间
刷题记录 452. 用最少数量的箭引爆气球思路一思路二 435. 无重叠区间763. 划分字母区间 452. 用最少数量的箭引爆气球 leetcode题目地址 思路一 先按起始坐标从小到大排序。排序后找交集并将交集存入一个数组中,遍历气球数组从交集数组中找交集,找到与…...

Ubuntu 下 Docker安装 2024
Ubuntu 下 Docker安装 2024 安装1.卸载老版本2.更新apt包索引3.安装必要工具包4.添加Docker GPG秘钥5.配置仓库源6.安装Docker Engine7.启动docker 国内镜像源下架的解决办法1.修改文件 /etc/docker/daemon.json2.换源3.查看是否换源成功4.重启 安装 1.卸载老版本 sudo apt-ge…...
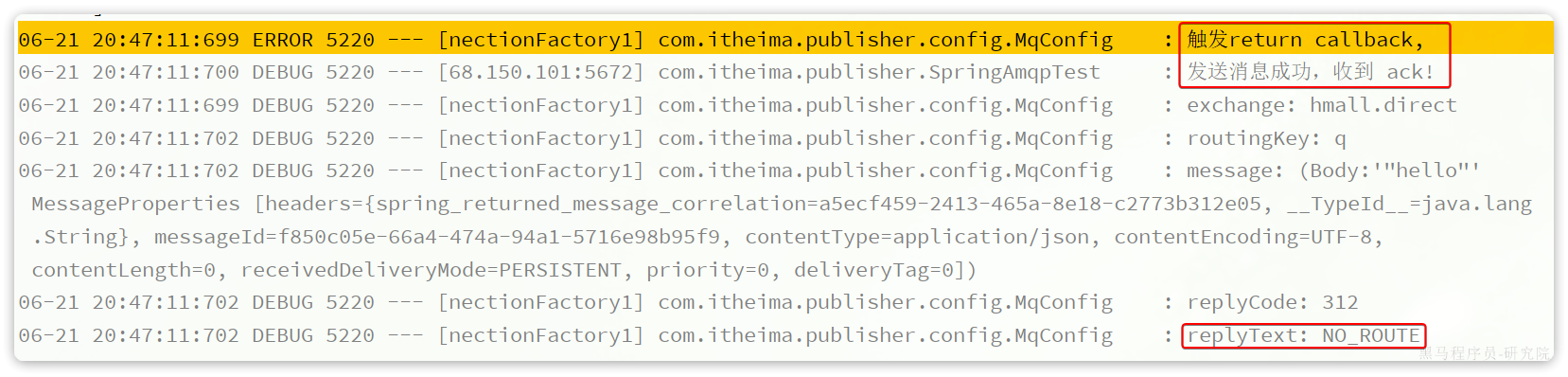
发送者的可靠性
这篇文章是了解MQ消息的可靠性,即:消息应该至少被消费者处理1次 那么问题来了: 我们该如何确保MQ消息的可靠性?如果真的发送失败,有没有其它的兜底方案? 首先,我们一起分析一下消息丢失的可能…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
