【蓝桥杯集训·每日一题】AcWing 4309. 消灭老鼠
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 最大公约数
一、题目
1、原题链接
4309. 消灭老鼠
2、题目描述
约翰的农场可以看作一个二维平面。
农场中有 n 个老鼠,在毁坏着农田。
第 i 个老鼠的位置坐标为 (xi,yi)。
不同老鼠可能位于同一位置。
在 (x0,y0) 处,装有一个双向发射的激光枪,该位置没有老鼠。
激光枪每次发射都可以将穿过点 (x0,y0) 的某一条直线上的所有老鼠都消灭掉。
请问,为了消灭所有老鼠,至少需要激光枪发射几次。
输入格式
第一行包含三个整数 n,x0,y0,表示共有 n 只老鼠,激光枪的位置为 (x0,y0)。
接下来 n 行,每行包含两个整数 xi,yi,表示第 i 只老鼠的位置为 (xi,yi)。
输出格式
一个整数,表示激光枪的最少发射次数。
数据范围
前 5 个测试点满足 1≤n≤5。
所有测试点满足 1≤n≤1000,−104≤xi,yi≤104。输入样例1:
4 0 0 1 1 2 2 2 0 -1 -1输出样例1:
2输入样例2:
2 1 2 1 1 1 0输出样例2:
1
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)我们可以先将发射点移动到原点,当某些点与发射点构成的直线的斜率相同时,说明可以将这些点上的老鼠一起消灭掉。
(2)由于可能有些点在x轴或者y轴上,所以计算斜率可能会出现除数为0的情况,所以我们用点对来存储每个点的斜率(即分子分母约分后最简分数形式的点对(分子与分母),也就是同时除以它俩的最大公约数)。而针对一条直线,可以同时消灭一、三象限或二、四象限点上在该直线上的所有老鼠,所以我们可以将二、四象限的点来原点对称到第一、四象限(针对两个点,如果某个点经过原点对称变换后和另外一个点重合,说明两点在同一条直线上),所以,这样我们只需要统计第一、四象限有多少个点对即可。
(3)最后统计一共有多少个不同的点对即可。
2、时间复杂度
时间复杂度为O(nlogn)(求最大公约数时间复杂度O(logn))
3、代码详解
#include <iostream>
#include <set>
#include <utility>
using namespace std;
typedef pair<int,int> PII; //存储每个点对
set<PII> s; //set去重来统计点对个数
int n,x0,y0;
//欧几里得算法求最大公约数
int gcd(int a,int b){return b?gcd(b,a%b):a;
}
int main(){cin>>n>>x0>>y0;while(n--){int x,y;cin>>x>>y;x-=x0,y-=y0; //将该点坐标更新成以(x0,y0)为原点的坐标系中点的坐标int d=gcd(x,y); //求两者的最大公约数x/=d,y/=d; //将y/x分子分母约分(分子分母同时除两者的最大公约数)后的点对放入set中if(x<0) x=-x,y=-y; //将第二、三象限的点原点对称到第一、四象限s.insert({x,y});}cout<<s.size();return 0;
}
三、知识风暴
最大公约数
- 求最大公约数可以利用欧几里得算法:即
gcd(a,b)=gcd(b,a mod b)。
相关文章:

【蓝桥杯集训·每日一题】AcWing 4309. 消灭老鼠
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴最大公约数一、题目 1、原题链接 4309. 消灭老鼠 2、题目描述 约翰的农场可以看作一个二维平面。 农场中有 n 个老鼠,在毁坏着农田。 第 i 个老鼠的位置坐标为…...

FPGA实现CSI-2 解码MIPI视频 2line 720P分辨率 OV5647采集 提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...
)
JS面试题收集(持续更新好中...)
1.JavaScript 中的垃圾回收机制 定义:指一块被分配的内存既不能使用,又不能回收,直到浏览器进程结束。 JavaScript在创建对象时会为它们分配内存,不再使用时会自动释放内存,这个过程称为垃圾收集。 四种常见的内存泄…...

2023携程面试题
Java I/O 面试前需要准备: 1. Java 八股文:了解常考的题型和回答思路; 2. 算法:刷 100-200 道题,记住刷题最重要的是要理解其思想,不要死记硬背,碰上原题很难,但 大多数的解题思…...

CANoe中使用CAPL函数接口调用Vflash文件
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...
三天吃透计算机网络面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
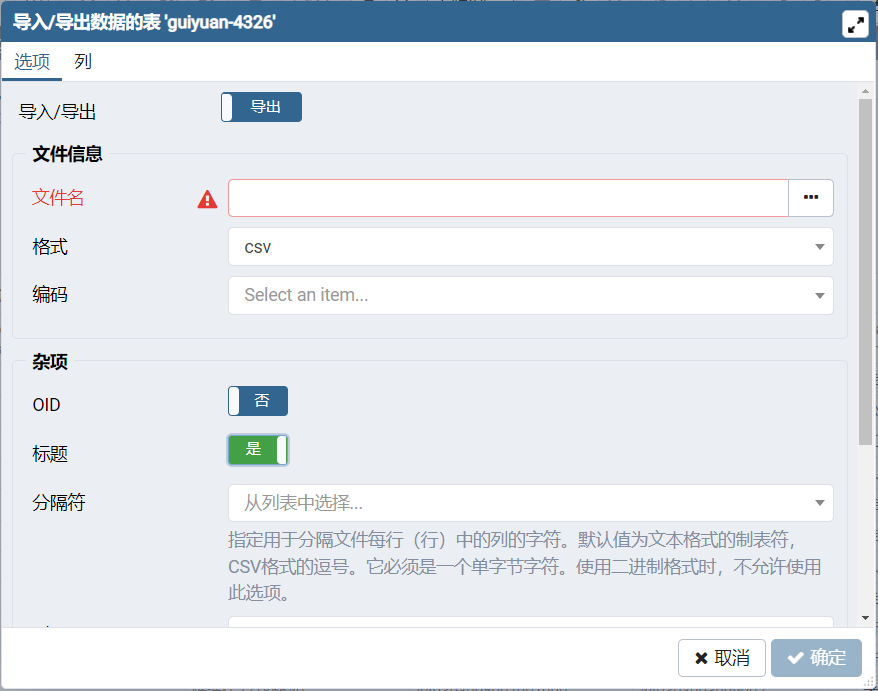
shp数据添加wkt字段并导出成csv,leaflet绘制使用
准备的东西:软件2跟软件3具体怎么有这些软件需要自行百度postgresql postgis相关 1.shp数据 2.软件2 3.软件3 1.数据导入 首先你得有软件2的数据库,即postgresql数据库,然后通过postgis的插件进行连接并导入数据, 导入数据…...
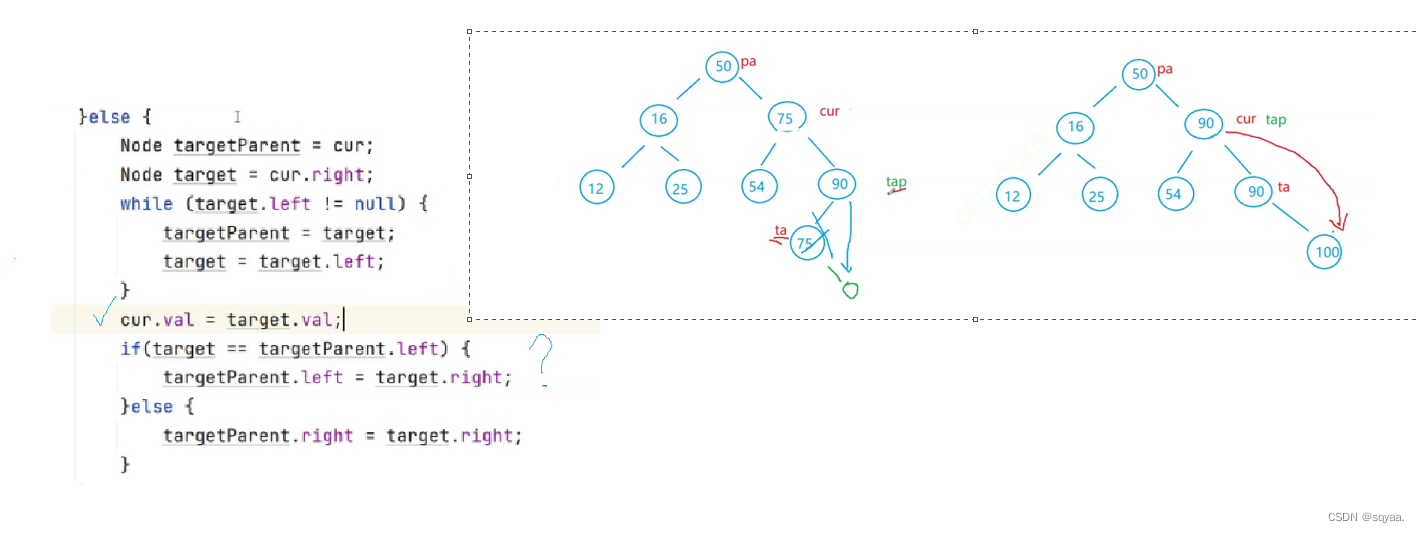
Java——二叉树的最近公共祖先及二叉搜索树介绍
目录 二叉树的最近公共祖先 题目 思路一:如果给定的是一颗二叉搜索树, 思路二:假设是孩子双亲表示法 二叉搜索树 定义Node类 查找 删除 插入 二叉树的最近公共祖先 题目 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百…...

Stable Diffusion加chilloutmixni真人图片生成模型,AI绘图杀疯了
上期图文教程,我们分享过AI绘图大模型Stable Diffusion以及中文版本文心AI绘画大模型的基础知识以及代码实现,截至到目前为止。Stable Diffusion模型已经更新到了V2.1版本,其文生图大模型也越来越火,其在2022年底,由AI绘制的图片被荣为国际大奖,让大家对AI绘画大模型也越…...

Matplotlib 绘图实用大全
本文只介绍最简单基本的画图方法 预设 要想画出来的图有些逼格,首先应该进行如下设置 plt.rcParams[font.sans-serif][SimHei] #画图时显示中文字体 plt.rcParams[axes.unicode_minus] False #防止因修改成中文字符,导致某些 unicode 字符不能…...
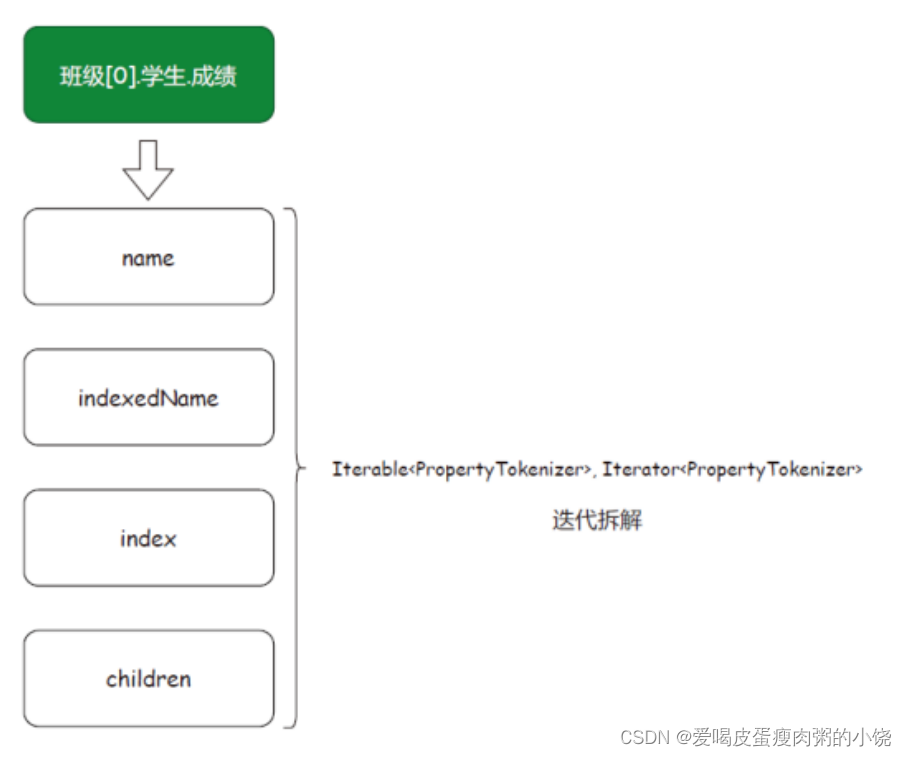
MyBatis源码用了哪些设计模式?
MyBatis源码用了哪些设计模式?前言一、创建型模式工厂模式单例模式建造者模式二、结构型模式适配器模式代理模式组合模式装饰器模式三、行为型模式模板模式策略模式迭代器模式总结前言 在 MyBatis 的两万多行的框架源码中,使用了大量的设计模式对工程架…...

【16.整数转罗马数字】
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例…...

前端小技巧
1.html 1.1 网站自动刷新 应用场景: 网页定期自动刷新(现在基本淘汰了,采用ajax);自动跳转到指定页面,这个自动跳转的好处就是不需要JS调用,属于纯html网页自动跳转 v7-网站自动刷新 你可以…...
Servlet2.0
文章目录更方便的部署方式安装插件使用插件验证程序常见访问出错的解决方案404错误405错误500错误空白页面无法访问此网站在文章 TomcatServlet初识中,我们通过七个大的步骤才可以完成一个简单的Servlet程序,这个过程无疑是非常繁琐的,那么我…...

【c++】继承
目录 一、继承的表现 子类对父类成员的访问权限 二、父类与子类之间的相互赋值 三、继承的作用域 如果是父类和子类构成隐藏呢? 四、子类的成员函数怎么写 1.default构造函数 2.析构函数 所以析构函数不需要我们显式调用。 五、继承与友元函数 六、继承与静…...

minio安装配置和使用(二)客户端安装
安装minio客户端mcli 命令如下: dnf install https://dl.minio.org.cn/client/mc/release/linux-amd64/mcli-20230128202938.0.0.x86_64.rpm 安装完成,在/usr/local/bin/下新增了mcli命令 mcli是对minio进行管理的命令。功能丰富, 基本格式…...

【如何使用Arduino设置GRBL和控制CNC机床】
【如何使用Arduino设置GRBL和控制CNC机床】 前言1. 什么是GRBL?2. 所需硬件3. 如何安装GRBL4. GRBL 配置5. GRBL 控制器5.1 如何使用通用 G 代码发送器5.2 波特率5.3 电机方向5.4 步进比例系数5.5 限位开关5.6 数控机床的归位设置6. 结论前言 如果您正在考虑或正在制造自己的…...
项目测试——博客系统
文章目录项目测试——博客系统项目简介项目功能测试计划web自动化测试1. 测试用例2.web自动化测试说明项目测试——博客系统 项目简介 博客系统主要分为8大模块,分别是注册页,登录页,编辑页,修改页,个人主页…...
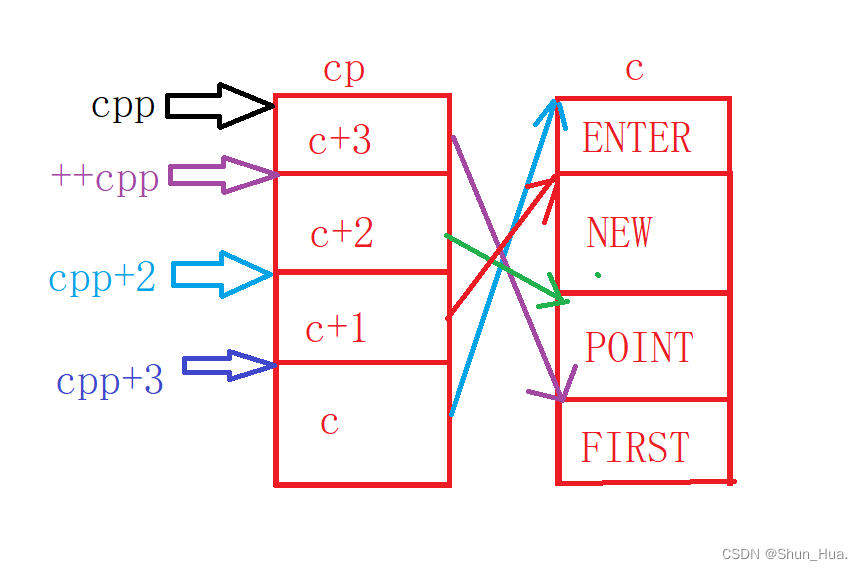
【C习题】经典数组与指针面试题(万字)
文章目录一. 一维数组二.字符数组三.字符指针四.二维数组五.指针笔试题一. 一维数组 首先说明:需熟记以下三个规则。 规则1.&数组名指的是取出整个数组的地址。 规则2.数组名被单独放在sizeof内部,计算的是整个数组的大小。 说明:这里的单…...
【ArcGIS Pro二次开发】(13):ProWindow的用法
ProWindow是ArcGIS Pro SDK中的一个WPF控件,具有以下特点: 可扩展性:ProWindow提供了丰富的API和样式,可以轻松地扩展和自定义ArcGIS Pro应用程序的UI。 可定制性:ProWindow支持多种UI控件和布局方式,可以…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
