了解股票沽空及其风险
什么是股票沽空?
股票沽空是一种投资策略,投资者通过借入股票并在市场上卖出,期望在未来以更低的价格买回股票,以赚取价差收益。这一策略在市场下跌时尤为常见,因为投资者可以从股票价格的下跌中获利。
股票沽空的时机
理想的沽空时机通常是在市场趋势明朗的情况下,尤其是跟随大型机构或知名投资者的行动。例如,在1997-1998年的亚洲金融风暴和2008年的国际金融海啸期间,许多投资者通过沽空股票获利 。
沽空的风险
与购买股票不同,股票沽空具有更高的风险。购买股票时,最大损失仅为投资金额,但沽空的潜在亏损是无限的。例如,如果沽空价值HKD 100,000的股票,而该股票价格升至HKD 1,000,000,投资者将面临HKD 900,000的亏损 。
对冲策略
对冲是一种通过持有不同资产以减少投资风险的策略。例如,投资者可以通过购买期权、期货或其他衍生工具来对冲股票的潜在风险。期权和期货是常见的对冲工具,可以帮助投资者在市场波动中保护他们的投资 。
替代沽空的工具
除了直接沽空股票,投资者还可以使用其他工具来实现类似的效果,如购买认沽期权(Put options)、卖出认购期权(Call options)或购买反向ETF等。这些工具可以在股票价格下跌时获利,同时限制潜在的损失 。
沽空的总结与建议
股票沽空作为一种高风险高回报的投资策略,需要投资者具备较高的市场判断力和风险承受能力。在选择沽空或其他对冲工具时,投资者应充分了解其运作原理和潜在风险,并根据自身的投资目标和风险承受能力做出决策 。 同时投资者也需要获得正确与即时的数据来作出正确的投资抉择。Alltick API提供实时与历史的市场数据,帮助投资者轻松了解外汇,贵金属,能源,股票,加密货币的实时及历史市场数据和走势,从而作出明智的投资抉择。
对于散户投资者,尤其是那些经验不足的投资者,建议在进行沽空或使用其他衍生工具前,先进行充分的市场研究和风险评估,并考虑咨询专业的财务顾问以制定合理的投资策略。
相关文章:

了解股票沽空及其风险
什么是股票沽空? 股票沽空是一种投资策略,投资者通过借入股票并在市场上卖出,期望在未来以更低的价格买回股票,以赚取价差收益。这一策略在市场下跌时尤为常见,因为投资者可以从股票价格的下跌中获利。 股票沽空的…...

【Sql Server修改列类型错误信息:对象名依赖于列】
Sql Server修改列类型错误信息:对象名依赖于列 报错信息解决方法测试sql语句 报错信息 修改表中列类型,发生报错如下: [SQL Server]对象DF__Forecast___isCal__4E746892 依赖于 列isCalcFinished。 (5074) [42000] [Microsoft][ODBC Driver…...

【ACM珠海分会,IEEE Fellow加盟,CPS出版】第四届管理科学和软件工程国际学术会议(ICMSSE 2024,7月19-21)
第四届管理科学和软件工程国际学术会议(ICMSSE 2024)由ACM珠海分会,广州番禺职业技术学院主办;全国区块链行业产教融合共同体,AEIC学术交流中心承办,将于2024年7月19-21日于广州召开。 会议旨在为从事管理与软件工程领域的专家学…...

kmeans.fit_predict 和 kmeans.fit有什么区别
KMeans 是 scikit-learn 库中用于执行 K-means 聚类算法的类。fit_predict 和 fit 是该类中的两个方法,的主要区别在于返回的内容和用途。 kmeans.fit: 用途: 用于训练 K-means 模型。输入: 接受一个特征矩阵(通常是二维数组)作为输入。输出:…...
香港优才计划续签难吗?一次性说清楚优才续签要求,不在香港居住也能续签成功!
香港优才计划续签难吗?这个问题对考虑申请优才的人来说,还是挺重要的。我们申请优才,最关注的2个问题,一个是获批,还有一个就是续签了。 毕竟我们费那么大功夫申请优才,可不只是为了一个为期3年的香港临时…...

react获取访问过的路由历史记录
看了下,好像没有很好的解决方案,之前的useHistory现在也用不了了, chatgpt说使用useMatch,也报错 看了下浏览器原生的。本来浏览器就会限制这个histroy的读取,只能获取length https://developer.mozilla.org/zh-CN/…...

基于深度学习的点云降噪
基于深度学习的点云降噪是一种利用深度学习模型处理三维点云数据,以去除噪声并恢复点云的原始形状和细节的方法。点云数据广泛应用于自动驾驶、机器人导航、3D扫描和虚拟现实(VR)等领域,因此高质量的点云数据处理至关重要。以下是…...

数据结构-二叉搜索树与红黑树
4.二叉搜索树 又叫二叉查找树、有序二叉树、排序二叉树。树中任意一个结点,其左子树的每个节点值都要小于该节点,其右子树的每个节点值都要大于该节点 作用:能够进行快速查找、插入、删除操作 4.1 二叉搜索树的时间复杂度 注:二…...

52771-009P 同轴连接器
型号简介 52771-009P是Southwest Microwave的连接器。这款连接器外导体外壳、耦合螺母和电缆夹紧螺母都采用了不锈钢 UNS-S30300 材料。不锈钢具有优异的耐腐蚀性和机械强度,能够保证连接器在各种恶劣环境下都能稳定工作。 型号特点 中心触点、外壳、衬套固定环&am…...

鸿蒙语言基础类库:【@ohos.util.Vector (线性容器Vector)】
线性容器Vector 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 Vect…...

使用Python绘制堆积面积图
使用Python绘制堆积面积图 堆积面积图效果代码 堆积面积图 堆积面积图是面积图的一种扩展,通过堆积多个区域展示不同类别数据的累积变化。常用于显示不同部分对整体的贡献。 效果 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pQbW4F…...

代码还原动态调试之 pstree 乘法变加法
乘法编译后,生成加法汇编,提升CPU执行效率; 406a: 85 ff test %edi,%edi // x ? 0406c: 0f 84 7e 00 00 00 je 40f0 <__sprintf_chkplt0x1980>*/int digits, div;if (x ! 0) {/*4072: 89 fd …...
)
C++:获取当前可执行核心数(开辟线程)
sysconf(_SC_NPROCESSORS_ONLN) 是一个在 POSIX 兼容系统上广泛使用的函数,它用于获取当前系统上可用的处理器(CPU 核心)的数量。这个函数是 sysconf 函数的一个特定调用,其中 _SC_NPROCESSORS_ONLN 是一个常量,指定了…...

【简历】吉林某985大学:JAVA实习简历指导,面试通过率相当低
注:为保证用户信息安全,姓名和学校等信息已经进行同层次变更,内容部分细节也进行了部分隐藏 简历说明 这份简历是一个顶级985吉林大学的同学投Java职位的简历。因为学校是顶级985,所以他的大厂简历通过率是比较高的,…...

C#中的MD5摘要算法与哈希算法
文章目录 一、哈希算法基础二、MD5 算法原理三、MD5摘要算法四、哈希算法五、C#实现示例MD5算法示例哈希算法示例字符串MD5值对比 六、总结 一、哈希算法基础 哈希算法是一种单向密码体制,它将任意长度的数据转换成固定长度的字符串。这种转换是不可逆的࿰…...

使用 python 构建企业级高可用海量爬虫调度系统
一、引言 在大数据时代,信息的获取与分析成为了企业决策的重要依据。对于营销行业而言,实时抓取和分析竞争对手动态、市场趋势以及用户反馈等数据,是制定有效策略的关键。然而,构建一个高可用的、能够处理海量数据的爬虫调度系统…...

IDEA常用技巧荟萃:精通开发利器的艺术
1 概述 在现代软件开发的快节奏环境中,掌握一款高效且功能全面的集成开发环境(IDE)是提升个人和团队生产力的关键。IntelliJ IDEA,作为Java开发者的首选工具之一,不仅提供了丰富的编码辅助功能,还拥有高度…...

GD32F303之CAN通信
1、CAN时钟 GD32F303主时钟频率最大是120Mhz,然后APB1时钟最大是60Mhz,APB2时钟最大是120Mhz,CAN挂载在APB1总线上面 所以一般CAN的时钟频率是60Mhz,这个频率和后面配置波特率有关 2、GD32F303时钟配置 首先我们知道芯片有几个时钟 HXTAL:高速外部时钟࿱…...

postgres 的dblink使用,远程连接数据库
一.安装下载 dblink create extension if not exists dblink 查看是否已经安装 select * from pg_extension;二.运行,查询数据 其中,第一个参数是dblink名字,也可以是连接字符串。 第二个参数是要执行的SQL查询语句。AS子句用于指定返回结…...

短视频矩阵系统是什么?怎么搭建短视频矩阵系统?一文了解矩阵模式
在数字时代,短视频已成为信息传播的新宠,而短视频矩阵系统则是品牌和个人在短视频领域取得突破的重要工具。那么,短视频矩阵系统究竟是什么?如何搭建这样一个高效的系统?它又能够解决哪些问题呢?本文将为您…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

GC1808:高性能音频ADC的卓越之选
在音频处理领域,高质量的音频模数转换器(ADC)是实现精准音频数字化的关键。GC1808,一款96kHz、24bit立体声音频ADC,以其卓越的性能和高性价比脱颖而出,成为众多音频设备制造商的理想选择。 GC1808集成了64倍…...

【前端实战】如何让用户回到上次阅读的位置?
目录 【前端实战】如何让用户回到上次阅读的位置? 一、总体思路 1、核心目标 2、涉及到的技术 二、实现方案详解 1、基础方法:监听滚动,记录 scrollTop(不推荐) 2、Intersection Observer 插入探针元素 3、基…...
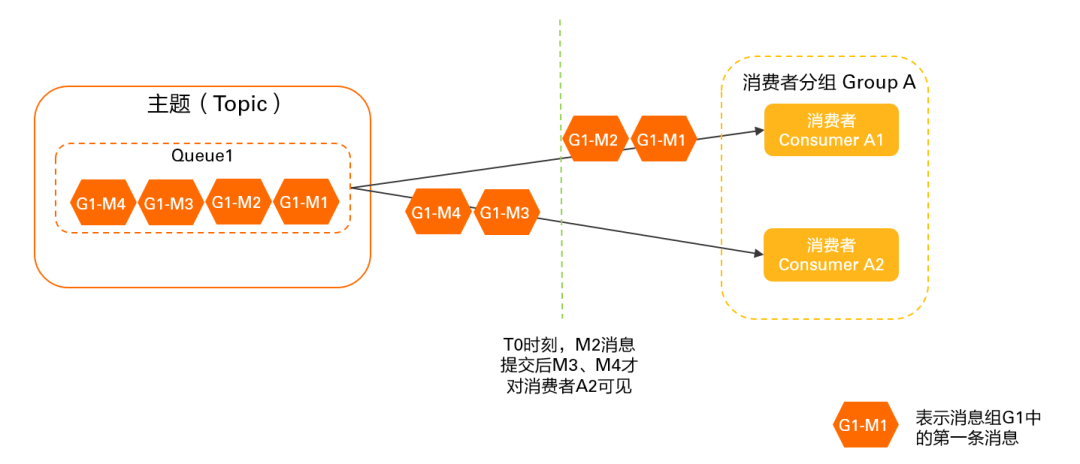
RocketMQ 客户端负载均衡机制详解及最佳实践
延伸阅读:🔍「RocketMQ 中文社区」 持续更新源码解析/最佳实践,提供 RocketMQ 专家 AI 答疑服务 前言 本文介绍 RocketMQ 负载均衡机制,主要涉及负载均衡发生的时机、客户端负载均衡对消费的影响(消息堆积/消费毛刺等…...

Razor编程中@Helper的用法大全
文章目录 第一章:Helper基础概念1.1 Helper的定义与作用1.2 Helper的基本语法结构1.3 Helper与HtmlHelper的区别 第二章:基础Helper用法2.1 无参数Helper2.2 带简单参数的Helper2.3 带默认值的参数2.4 使用模型作为参数 第三章:高级Helper用法…...
