Codeforces Round 954 (Div. 3)
🚀欢迎来到本文🚀
🍉个人简介:陈童学哦,彩笔ACMer一枚。
🏀所属专栏:Codeforces
本文用于记录回顾本彩笔的解题思路便于加深理解。
📢📢📢传送阵
- A. X Axis
- 解题思路:
- AC代码:
- B. Matrix Stabilization
- 解题思路:
- AC代码:
- C. Update Queries
- 解题思路:
- AC代码:
- D. Mathematical Problem
- 解题思路:
- AC代码:
- E. Beautiful Array
- 解题思路:
- AC代码:
A. X Axis
You are given three points with integer coordinates x 1 x_1 x1, x 2 x_2 x2, and x 3 x_3 x3 on the X X X axis ( 1 ≤ x i ≤ 10 1 \leq x_i \leq 10 1≤xi≤10). You can choose any point with an integer coordinate a a a on the X X X axis. Note that the point a a a may coincide with x 1 x_1 x1, x 2 x_2 x2, or x 3 x_3 x3. Let f ( a ) f(a) f(a) be the total distance from the given points to the point a a a. Find the smallest value of f ( a ) f(a) f(a).
The distance between points a a a and b b b is equal to ∣ a − b ∣ |a - b| ∣a−b∣. For example, the distance between points a = 5 a = 5 a=5 and b = 2 b = 2 b=2 is 3 3 3.

Input
Each test consists of multiple test cases. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 3 1 \leq t \leq 10^3 1≤t≤103) — the number of test cases. Then follows their descriptions.
The single line of each test case contains three integers x 1 x_1 x1, x 2 x_2 x2, and x 3 x_3 x3 ( 1 ≤ x i ≤ 10 1 \leq x_i \leq 10 1≤xi≤10) — the coordinates of the points.

Output
For each test case, output the smallest value of f ( a ) f(a) f(a).

解题思路:
可以通过暴力枚举出来最佳的那个点,然后计算答案,但是这里我们其实可以发现f(a)的最小值其实就是a为x1、x2、x3三个点中从小到大排序中间的那个点。
AC代码:
#include<bits/stdc++.h>
#define look(x) cout << #x << " == " << x << "\n"
using namespace std;
using i64 = long long;
using ld = long double;
const int N = 2e5 + 10;
const int MOD1 = 1e9 + 7;
const int MOD2 = 998244353;
void solve(){int a[3];cin >> a[0] >> a[1] >> a[2];sort(a,a + 3);cout << a[1] - a[0] + a[2] - a[1] << "\n";
}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while(t --){solve();}return 0;
}
B. Matrix Stabilization
You are given a matrix of size n × m n \times m n×m, where the rows are numbered from 1 1 1 to n n n from top to bottom, and the columns are numbered from 1 1 1 to m m m from left to right. The element at the intersection of the i i i-th row and the j j j-th column is denoted by a i j a_{ij} aij.
Consider the algorithm for stabilizing matrix a a a:
- Find the cell ( i , j ) (i, j) (i,j) such that its value is strictly greater than the values of all its neighboring cells. If there is no such cell, terminate the algorithm. If there are multiple such cells, choose the cell with the smallest value of i i i, and if there are still multiple cells, choose the one with the smallest value of j j j.
- Set a i j = a i j − 1 a_{ij} = a_{ij} - 1 aij=aij−1.
- Go to step 1 1 1.
In this problem, cells ( a , b ) (a, b) (a,b) and ( c , d ) (c, d) (c,d) are considered neighbors if they share a common side, i.e., ∣ a − c ∣ + ∣ b − d ∣ = 1 |a - c| + |b - d| = 1 ∣a−c∣+∣b−d∣=1.
Your task is to output the matrix a a a after the stabilization algorithm has been executed. It can be shown that this algorithm cannot run for an infinite number of iterations.

Input
Each test consists of multiple sets of input data. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of sets of input data. This is followed by their description.
The first line of each set of input data contains two integers n n n and m m m (KaTeX parse error: Expected 'EOF', got '&' at position 33: …100, n \cdot m &̲gt; 1) — the number of rows and columns of matrix a a a.
The next n n n lines describe the corresponding rows of the matrix. The i i i-th line contains m m m integers a i 1 , a i 2 , … , a i m a_{i1}, a_{i2}, \ldots, a_{im} ai1,ai2,…,aim ( 1 ≤ a i j ≤ 1 0 9 1 \leq a_{ij} \leq 10^9 1≤aij≤109).
It is guaranteed that the sum of n ⋅ m n \cdot m n⋅m over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.

Output
For each set of input data, output n n n lines with m m m numbers in each line — the values of the cells of matrix a a a after the stabilization algorithm.

解题思路:
从上往下从左往右依次遍历,如果当前数满足条件(严格大于它上、下、左、右的四个数)时,就将当前数设置为它上、下、左、右的四个数中的最大值。
AC代码:
#include<bits/stdc++.h>
#define look(x) cout << #x << " == " << x << "\n"
using namespace std;
using i64 = long long;
using ld = long double;
const int N = 2e5 + 10;
const int MOD1 = 1e9 + 7;
const int MOD2 = 998244353;
int g[110][110];
void solve(){int n,m;cin >> n >> m;for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){cin >> g[i][j];}}for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){if(g[i][j] > g[i - 1][j] && g[i][j] > g[i + 1][j] && g[i][j] > g[i][j + 1] && g[i][j] > g[i][j - 1]){g[i][j] = max({g[i - 1][j],g[i + 1][j],g[i][j - 1],g[i][j + 1]});}}}for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){cout << g[i][j] << " ";}cout << "\n";}for(int i = 0;i < 110;i ++){for(int j = 0;j < 110;j ++){g[i][j] = 0;}}
}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while(t --){solve();}return 0;
}
C. Update Queries
Let’s consider the following simple problem. You are given a string s s s of length n n n, consisting of lowercase Latin letters, as well as an array of indices i n d ind ind of length m m m ( 1 ≤ i n d i ≤ n 1 \leq ind_i \leq n 1≤indi≤n) and a string c c c of length m m m, consisting of lowercase Latin letters. Then, in order, you perform the update operations, namely, during the i i i-th operation, you set s i n d i = c i s_{ind_i} = c_i sindi=ci. Note that you perform all m m m operations from the first to the last.
Of course, if you change the order of indices in the array i n d ind ind and/or the order of letters in the string c c c, you can get different results. Find the lexicographically smallest string s s s that can be obtained after m m m update operations, if you can rearrange the indices in the array i n d ind ind and the letters in the string c c c as you like.
A string a a a is lexicographically less than a string b b b if and only if one of the following conditions is met:
- a a a is a prefix of b b b, but a ≠ b a \neq b a=b;
- in the first position where a a a and b b b differ, the symbol in string a a a is earlier in the alphabet than the corresponding symbol in string b b b.

Input
Each test consists of several sets of input data. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of sets of input data. Then follows their description.
The first line of each set of input data contains two integers n n n and m m m ( 1 ≤ n , m ≤ 1 0 5 1 \leq n, m \leq 10^5 1≤n,m≤105) — the length of the string s s s and the number of updates.
The second line of each set of input data contains a string s s s of length n n n, consisting of lowercase Latin letters.
The third line of each set of input data contains m m m integers i n d 1 , i n d 2 , … , i n d m ind_1, ind_2, \ldots, ind_m ind1,ind2,…,indm ( 1 ≤ i n d i ≤ n 1 \leq ind_i \leq n 1≤indi≤n) — the array of indices i n d ind ind.
The fourth line of each set of input data contains a string c c c of length m m m, consisting of lowercase Latin letters.
It is guaranteed that the sum of n n n over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105. Similarly, the sum of m m m over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.\

Output
For each set of input data, output the lexicographically smallest string s s s that can be obtained by rearranging the indices in the array i n d ind ind and the letters in the string c c c as you like.

解题思路:
我们想得到字典序最小的字符串,首先的话我们肯定是尽量想让字符串c中字典序小的字母尽可能的去替换原字符串索引位置靠前的字母,这样才能保证字典序最小,但是我们需要考虑到问题就是题目所给的索引数组ind中的数可能是相等的,也就意味着如果出现两个相同索引连续出现两次以上的话,当我们先去用字符串c中字典序更小的字母去替换的时候下次再次替换时会导致这个地方的字典序不是最小的。那么考虑如何解决这个弊端呢,这里可以考虑使用双指针,当出现两个相同以上的索引时,我们可以先从字符串c的尾指针先开始替换,这样就能保证下次替换的时候是字典序更小的字母替换更大的,而不是字典序小的被字典序大的替换掉。
AC代码:
#include<bits/stdc++.h>
#define look(x) cout << #x << " == " << x << "\n"
using namespace std;
using i64 = long long;
using ld = long double;
const int N = 2e5 + 10;
const int MOD1 = 1e9 + 7;
const int MOD2 = 998244353;
void solve(){int n,m;cin >> n >> m;string s1,s2;cin >> s1;int n1 = s1.size();s1 = '?' + s1;
// look(s1);vector<int> a(m + 1);for(int i = 1;i <= m;i ++){cin >> a[i];}cin >> s2;int n2 = s2.size();sort(s2.begin(),s2.end());
// look(s2);s2 = '?' + s2;
// look(s2);sort(a.begin() + 1,a.end());int l = 1,r = n2;
// look(a[1]);
// look(a[2]);for(int i = 1;i <= m;i ++){if(i != m && a[i] == a[i + 1]){
// look(s1);s1[a[i]] = s2[r];r --;} if(i == m){s1[a[i]] = s2[l];break;}if(a[i] != a[i + 1]){
// look(i);
// look(s1);s1[a[i]] = s2[l];l ++;}}
// look(s1);cout << s1.substr(1,n1) << "\n";}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while(t --){solve();}return 0;
}
D. Mathematical Problem
You are given a string s s s of length KaTeX parse error: Expected 'EOF', got '&' at position 3: n &̲gt; 1, consisting of digits from 0 0 0 to 9 9 9. You must insert exactly n − 2 n - 2 n−2 symbols + + + (addition) or × \times × (multiplication) into this string to form a valid arithmetic expression.
In this problem, the symbols cannot be placed before the first or after the last character of the string s s s, and two symbols cannot be written consecutively. Also, note that the order of the digits in the string cannot be changed. Let’s consider s = 987009 s = 987009 s=987009:
- From this string, the following arithmetic expressions can be obtained: 9 × 8 + 70 × 0 + 9 = 81 9 \times 8 + 70 \times 0 + 9 = 81 9×8+70×0+9=81, 98 × 7 × 0 + 0 × 9 = 0 98 \times 7 \times 0 + 0 \times 9 = 0 98×7×0+0×9=0, 9 + 8 + 7 + 0 + 09 = 9 + 8 + 7 + 0 + 9 = 33 9 + 8 + 7 + 0 + 09 = 9 + 8 + 7 + 0 + 9 = 33 9+8+7+0+09=9+8+7+0+9=33. Note that the number 09 09 09 is considered valid and is simply transformed into 9 9 9.
- From this string, the following arithmetic expressions cannot be obtained: + 9 × 8 × 70 + 09 +9 \times 8 \times 70 + 09 +9×8×70+09 (symbols should only be placed between digits), 98 × 70 + 0 + 9 98 \times 70 + 0 + 9 98×70+0+9 (since there are 6 6 6 digits, there must be exactly 4 4 4 symbols).
The result of the arithmetic expression is calculated according to the rules of mathematics — first all multiplication operations are performed, then addition. You need to find the minimum result that can be obtained by inserting exactly n − 2 n - 2 n−2 addition or multiplication symbols into the given string s s s.

Input
Each test consists of multiple test cases. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of test cases. Then follows their description.
The first line of each test case contains a single integer n n n ( 2 ≤ n ≤ 20 2 \leq n \leq 20 2≤n≤20) — the length of the string s s s.
The second line of each test case contains a string s s s of length n n n, consisting of digits from 0 0 0 to 9 9 9.

Output
For each test case, output the minimum result of the arithmetic expression that can be obtained by inserting exactly n − 2 n - 2 n−2 addition or multiplication symbols into the given string.

解题思路:
长度为n的字符串插入n-2个符号,首先n为2是就是当前字符串转换为十进制数的结果,否则的话就是n-1个数字与n-2个符号之间的运算,n个字符组成n-1个数,显然必有一个数为两位数其余都为一位数,那么当n > 2时我们可以从左往右依次枚举相邻两位组成一个两位数时的与其他数进行加、乘运算的最小值,如果有0出现那么最小值必然为0,其次有1出现的话相乘能让结果不变,其余数均相加即可让值最小,最后在枚举的所有情况中取最小值即位答案。
AC代码:
#include<bits/stdc++.h>
#define look(x) cout << #x << " == " << x << "\n"
using namespace std;
using i64 = long long;
using ld = long double;
const int N = 2e5 + 10;
const int MOD1 = 1e9 + 7;
const int MOD2 = 998244353;
void solve(){int n;cin >> n;string s;cin >> s;if(n == 2){cout << stoi(s) << "\n";return;}int ans = 1e9;map<int,int> mp;for(int i = 0;i < n - 1;i ++){int x = stoi(s.substr(i,2));int sum = 0;sum += x;mp[i] = 1;mp[i + 1] = 1;for(int i = 0;i < n;i ++){if(!mp[i]){int y = (s[i] - '0');if(y == 0){cout << "0\n";return;}if(sum == 1){sum *= y;continue;} if(y != 1){sum += y;}}}ans = min(ans,sum);mp.clear();}cout << ans << "\n";
}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while(t --){solve();}return 0;
}
E. Beautiful Array
You are given an array of integers a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an and an integer k k k. You need to make it beautiful with the least amount of operations.
Before applying operations, you can shuffle the array elements as you like. For one operation, you can do the following:
- Choose an index 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n,
- Make a i = a i + k a_i = a_i + k ai=ai+k.
The array b 1 , b 2 , … , b n b_1, b_2, \ldots, b_n b1,b2,…,bn is beautiful if b i = b n − i + 1 b_i = b_{n - i + 1} bi=bn−i+1 for all 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n.
Find the minimum number of operations needed to make the array beautiful, or report that it is impossible.

Input
Each test consists of several sets of input data. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of sets of input data. Then follows their description.
The first line of each set of input data contains two integers n n n and k k k ( 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105, 1 ≤ k ≤ 1 0 9 1 \leq k \leq 10^9 1≤k≤109) — the size of the array a a a and the number k k k from the problem statement.
The second line of each set of input data contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an ( 1 ≤ a i ≤ 1 0 9 1 \leq a_i \leq 10^9 1≤ai≤109) — the elements of the array a a a.
It is guaranteed that the sum of n n n over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.

Output
For each set of input data, output the minimum number of operations needed to make the array beautiful, or − 1 -1 −1 if it is impossible.

解题思路:
要构造漂亮数组,首先如果一个数出现的次数如果为偶数的话,我们就不需要进行操作,否则的话我们需要使用一个map里套vector的map<int,vector>的结构来将ai%k相等的数存在同一个vector中,因为只有余数相等的两个数才能通过相加或相减若干倍的k才能得到。然后我们遍历map这个结构,如果有两个以上的vector的大小为奇数的话那么我们必然无法构造漂亮数组,因为我们最多将一个数放在整个数组的中间来让这个数成为回文中心而不用依靠两两配对完成,而出现两个以上的奇数大小的vector时,两个vector各自中多出来的那个数必然无法通过加减k来完成配对,所以此时必然无法完成构造。而如果上述条件满足的话,当vector的大小为偶数时,我们只需要从小到大依次取两个数使得两个数的差值尽可能的小,这样我们的操作数也会尽可能的小,但是当vector的大小为奇数时我们处理结果时会有些麻烦,因为我们不知道vector中的哪个数作为中心数能够使得结果最佳,如果我们暴力枚举vector中的每个数字作为中心数的话复杂度必然会爆炸,所以这里我们考虑使用前缀、后缀记录值的巧妙方法来降低复杂度。
AC代码:
#include<bits/stdc++.h>
#define look(x) cout << #x << " == " << x << "\n"
using namespace std;
using i64 = long long;
using ld = long double;
const int N = 2e5 + 10;
const int MOD1 = 1e9 + 7;
const int MOD2 = 998244353;
void solve(){int n,k;cin >> n >> k;vector<int> a(n + 1);map<int,int> mp;for(int i = 1;i <= n;i ++){cin >> a[i];mp[a[i]] ++;}map<int,vector<int>> mv;for(auto [x,y] : mp){if(y & 1){mv[x % k].push_back(x);}}i64 ans = 0;int res = 0;for(auto [x,y] : mv){if(y.size() & 1){res ++;if(res > 1){cout << "-1\n";return;}}sort(y.begin(),y.end());if(y.size() % 2 == 0){for(int i = 1;i < y.size();i += 2){int x = y[i] - y[i - 1];ans += x / k;}}else if(y.size() > 1){int m = (int)y.size();vector<i64> sum1(m);vector<i64> sum2(m);sum1[1] = y[1] - y[0];for(int i = 3;i < m;i += 2){sum1[i] = sum1[i - 2] + y[i] - y[i - 1];}sum2[m - 2] = y[m - 1] - y[m - 2];for(int i = m - 4;i >= 0;i -= 2){sum2[i] = sum2[i + 2] + y[i + 1] - y[i];}i64 tmp = min(sum1[m - 2],sum2[1]);for(int i = 2;i < m - 2;i += 2){tmp = min(tmp,sum1[i - 1] + sum2[i + 1]);}ans += tmp / k;}}cout << ans << "\n";}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while(t --){solve();}return 0;
}
相关文章:

Codeforces Round 954 (Div. 3)
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,彩笔ACMer一枚。 🏀所属专栏:Codeforces 本文用于记录回顾本彩笔的解题思路便于加深理解。 📢📢📢传送阵 A. X Axis解…...

【Django】报错‘staticfiles‘ is not a registered tag library
错误截图 错误原因总结 在django3.x版本中staticfiles被static替换了,所以这地方换位static即可完美运行 错误解决...
LeetCode 算法:二叉树的最近公共祖先 III c++
原题链接🔗:二叉树的最近公共祖先 难度:中等⭐️⭐️ 题目 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点…...

Windows CMD 命令汇总表
Windows CMD 命令汇总表 Windows CMD 命令汇总表目录操作磁盘操作文件操作其他命令FTP 命令高级系统命令批处理命令网络命令安全和权限命令 Windows CMD 命令指南目录操作MD - 创建子目录CD - 切换当前目录RD - 删除子目录DIR - 显示目录内容PATH - 设置可执行文件的搜索路径TR…...

【python+appium】自动化测试
pythonappium自动化测试系列就要告一段落了,本篇博客咱们做个小结。 首先想要说明一下,APP自动化测试可能很多公司不用,但也是大部分自动化测试工程师、高级测试工程师岗位招聘信息上要求的,所以为了更好的待遇,我们还…...
vue 数据类型
文章目录 ref 创建:基本类型的响应式数据reactive 创建:对象类型的响应式数据ref 创建:对象类型的响应式数据ref 对比 reactive将一个响应式对象中的每一个属性,转换为ref对象(toRefs 与 toRef)computed (根据计算进行修改) ref 创…...
)
MySQL(基础篇)
DDL (Data Definition Language) 数据定义语言,用来定义数据库对象(数据库,表, 字段) DML (Data Manipulation Languag) 数据操作语言,用来对数据库表中的数据进行增删改 DQL (Data Query Language) 数据查询语言,用…...
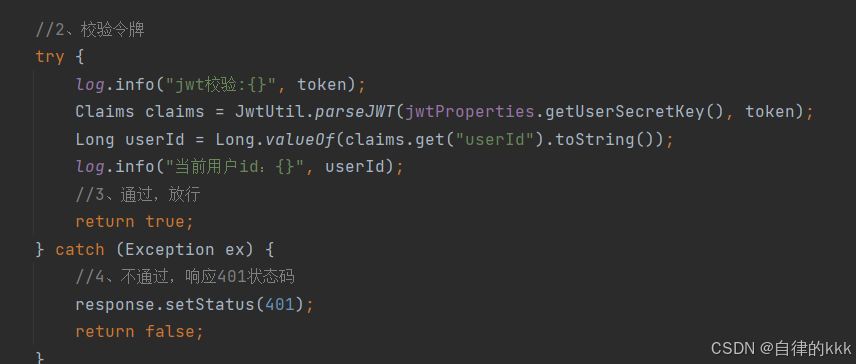
springboot中通过jwt令牌校验以及前端token请求头进行登录拦截实战
前言 大家从b站大学学习的项目侧重点好像都在基础功能的实现上,反而一个项目最根本的登录拦截请求接口都不会写,怎么拦截?为什么拦截?只知道用户登录时我后端会返回一个token,这个token是怎么生成的,我把它…...

从零开始开发视频美颜SDK:实现直播美颜效果
因此,开发一款从零开始的视频美颜SDK,不仅可以节省成本,还能根据具体需求进行个性化调整。本文将介绍从零开始开发视频美颜SDK的关键步骤和实现思路。 一、需求分析与技术选型 在开发一款视频美颜SDK之前,首先需要进行详细的需求…...

极验语序点选验证码识别(一)
注意,本文只提供学习的思路,严禁违反法律以及破坏信息系统等行为,本文只提供思路 极验文字点选验证码不必多说,很多小伙伴,借助标注工具或者打码平台标注完数据集后,使用开源的目标检测网络即可完成,欢迎收看我之前的文章: Pytorch利用ddddocr辅助识别点选验证码 或者使…...
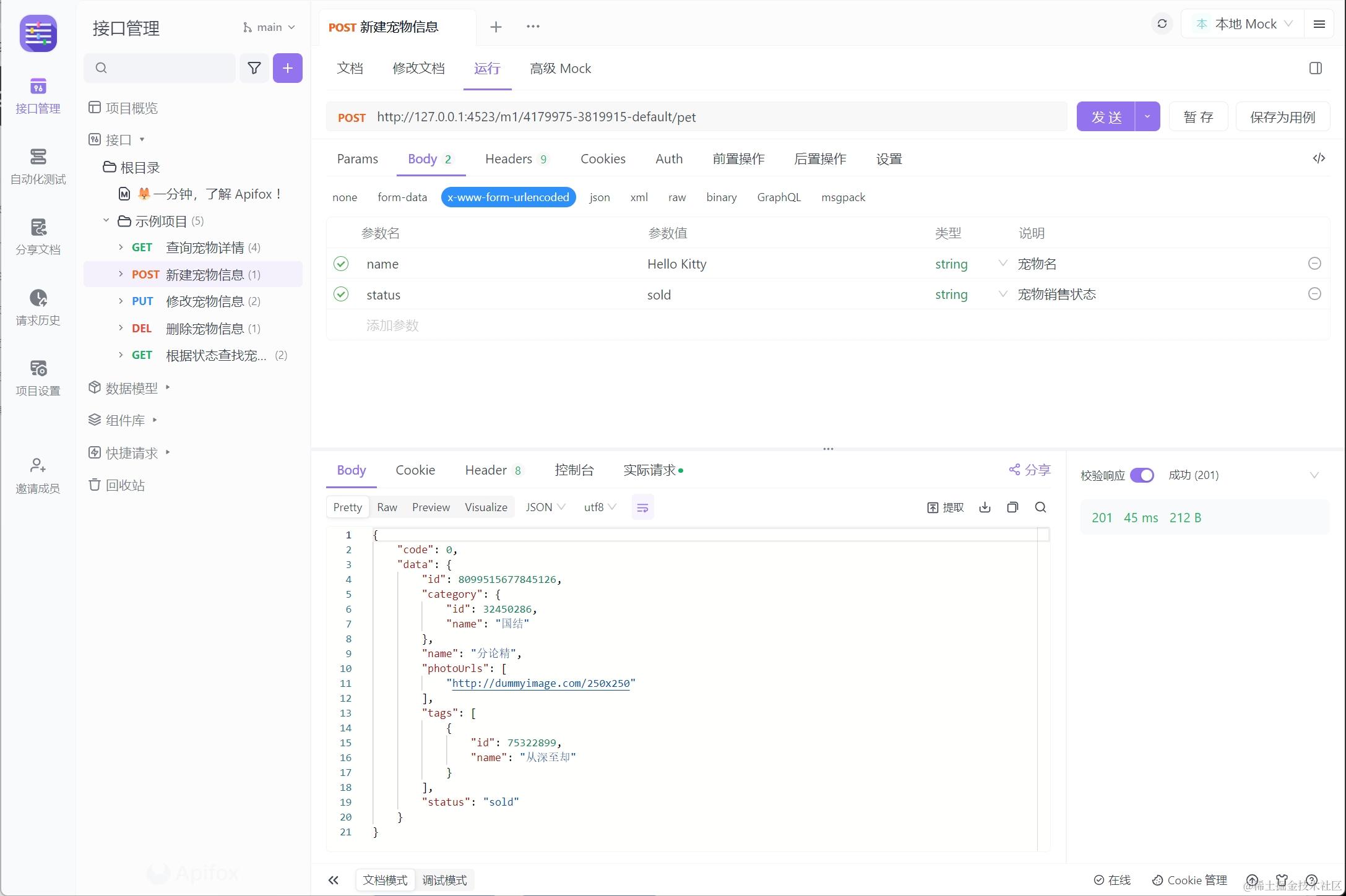
什么是 HTTP POST 请求?初学者指南与示范
在现代网络开发领域,理解并应用 HTTP 请求 方法是基本的要求,其中 "POST" 方法扮演着关键角色。 理解 POST 方法 POST 方法属于 HTTP 协议的一部分,主旨在于向服务器发送数据以执行资源的创建或更新。它与 GET 方法区分开来&…...
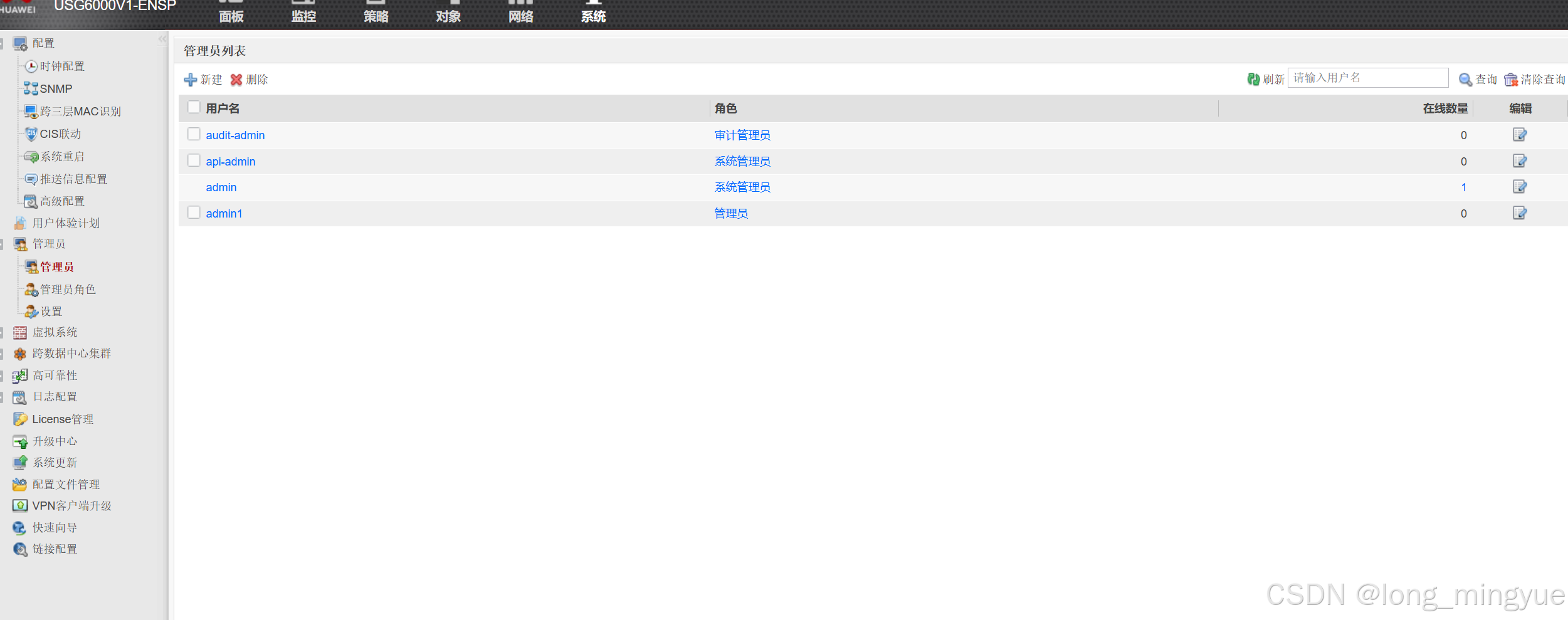
第一次作业
任务需求:1.DMz区内的服务器,办公区仅能在办公时间内(9-18)可以访问,生产区的设备全天可以访问 2.生产区不允许访问互联网,办公区和游客区可以访问互联网 3.办公区设备10.0.2.10不允许访问DMZ区的FTP服务器和http服务器,仅能ping通…...

【机器学习】12.十大算法之一支持向量机(SVM - Support Vector Machine)算法原理讲解
【机器学习】12.十大算法之一支持向量机(SVM - Support Vector Machine)算法原理讲解 一摘要二个人简介三基本概念四支持向量与超平面4.1 超平面(Hyperplane)4.2 支持向量(Support Vectors)4.3 核技巧&…...

使用 `useAppConfig` :轻松管理应用配置
title: 使用 useAppConfig :轻松管理应用配置 date: 2024/7/11 updated: 2024/7/11 author: cmdragon excerpt: 摘要:本文介绍了Nuxt开发中useAppConfig的使用,它便于访问和管理应用配置,支持动态加载资源、环境配置切换、权限…...
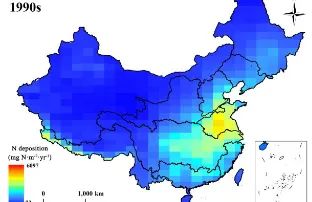
中国内陆水体氮沉降数据集(1990s-2010s)
全球大气氮沉降急剧增加对内陆水生态系统产生不良影响。中国是全球三大氮沉降热点地区之一,为了充分了解氮沉降对中国内陆水体的影响,制定合理的水污染治理方案,我们需要清楚的量化内陆水体的氮沉降通量。为此,我们利用LMDZ-OR-IN…...

qml 实现一个带动画的switch 按钮
一.效果图 》 二.qml 代码 import QtQuick 2.12 import QtQuick.Controls 2.12Switch {id: controlimplicitWidth: 42implicitHeight: 20indicator: Rectangle {id: bkRectangleanchors.fill: parentx: control.leftPaddingy: parent.height / 2 - height / 2radius: height …...
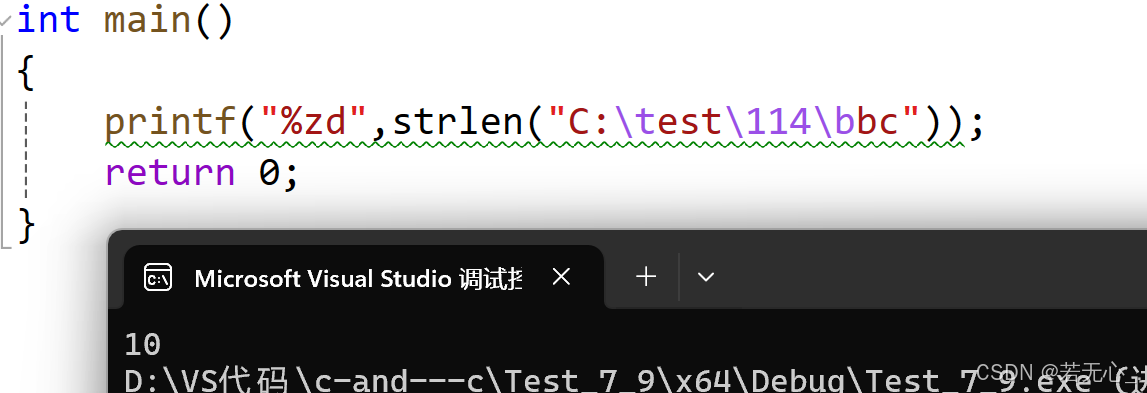
C语言基本概念
C语言是什么? 1.人与人之间 自然语言 2.人与计算机之间 计算机语言 例如C、Java、Go、Python 在计算机语言中 1.解释型语言:Python 2.编译型语言:C/C 编译和链接 C语言源代码都是文本文件.c,必须通过编译器的编译和链接器的…...

同轴多芯旋转电连接器1
什么是旋转电连接器? 旋转电连接器,亦称电气旋转接头或滑环,主要用于电气工程领域。其作用是在固定部件与旋转部件之间传输电信号、电源或数据,从而避免因旋转而引起的电线拉伤或缠结问题。这类连接器对于需要在旋转的同时进行电…...

android 消除内部保存的数据
在Android中,有多种方式可以消除应用内部保存的数据。这些数据可能存储在SharedPreferences、SQLite数据库、文件(包括缓存文件)或Content Providers中。以下是几种常见的方法来消除这些数据: SharedPreferences: 要删…...
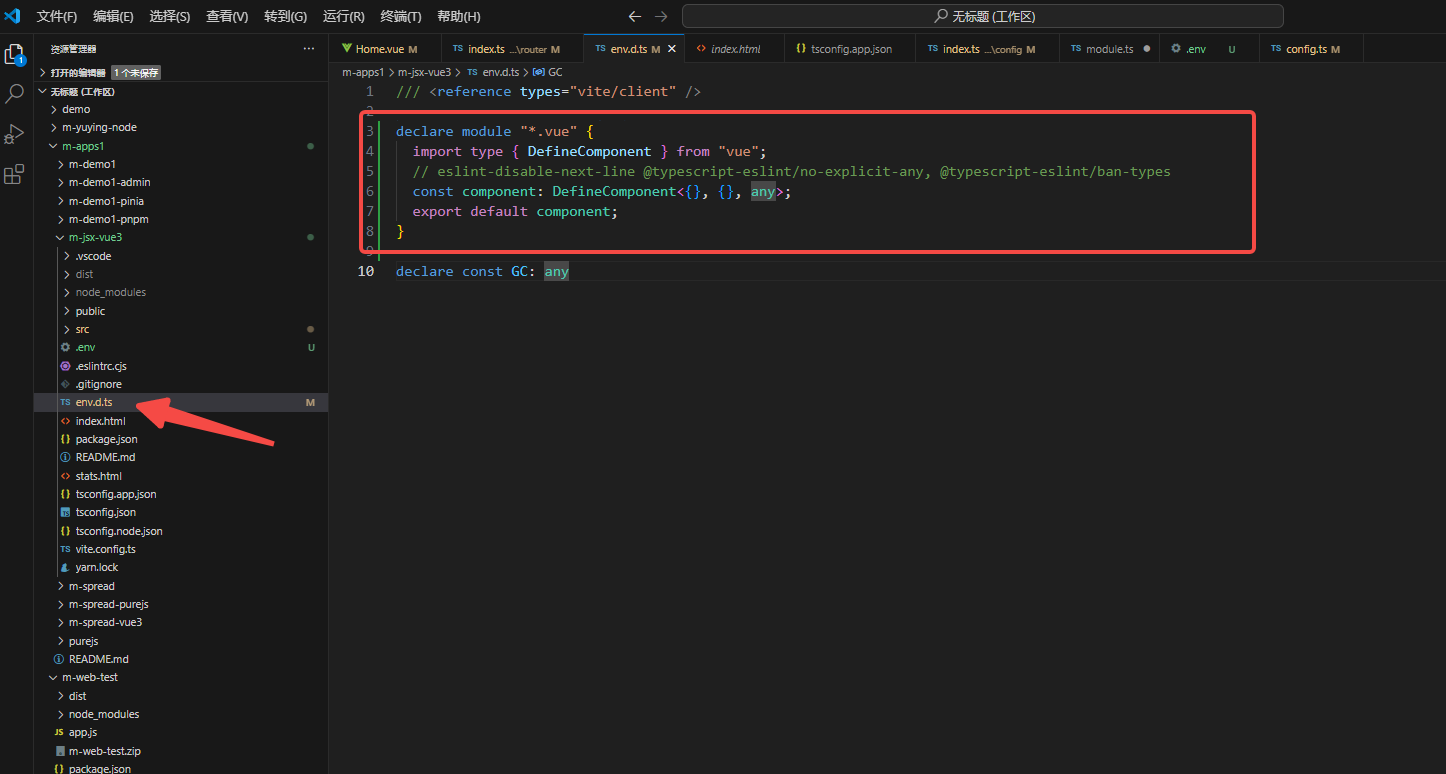
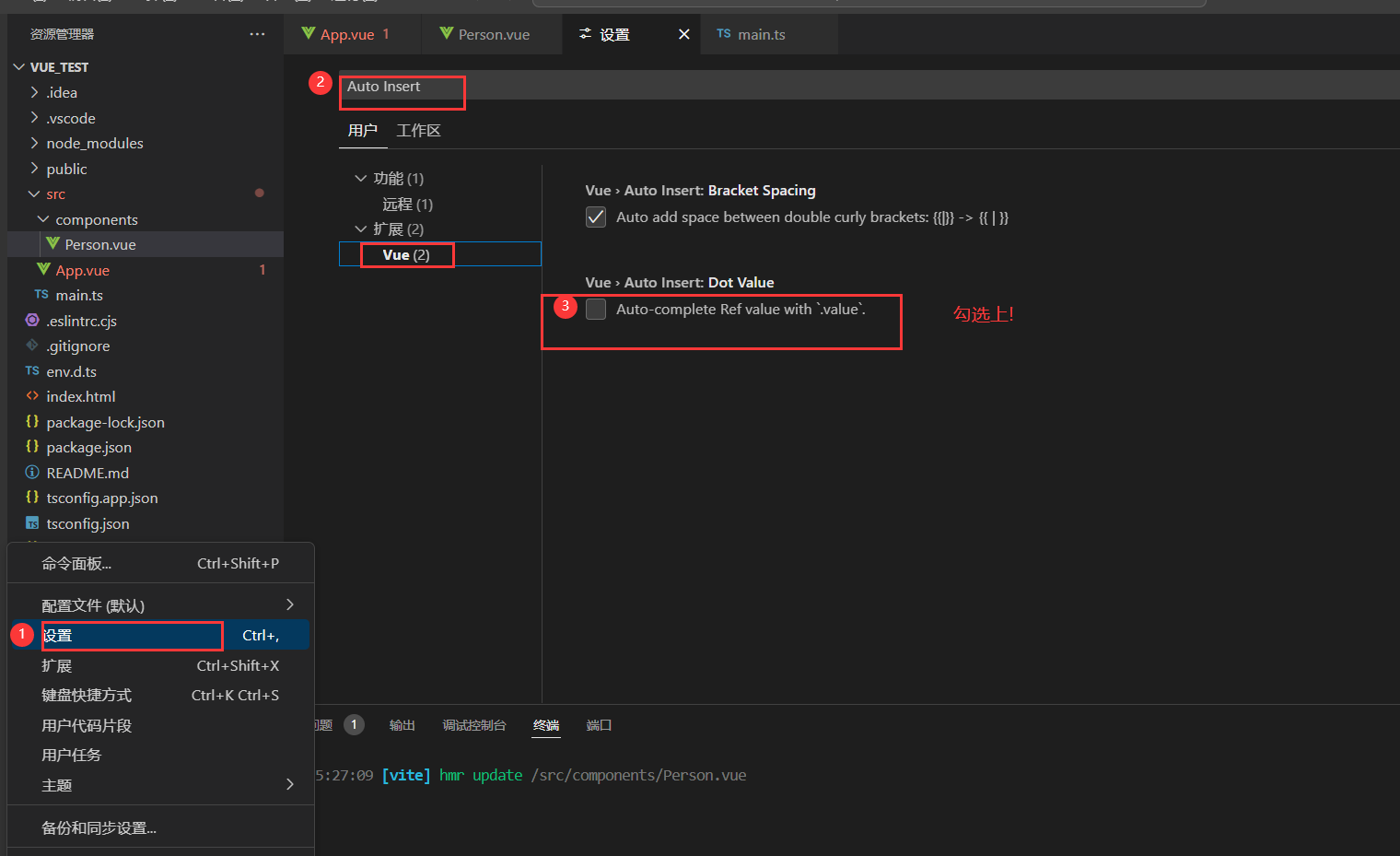
vue3 ts 报错:无法找到模块“../views/index/Home.vue”的声明文件
解决办法: env.d.ts 新增代码片段: declare module "*.vue" {import type { DefineComponent } from "vue";// eslint-disable-next-line typescript-eslint/no-explicit-any, typescript-eslint/ban-typesconst component: Define…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
