排序(二)——快速排序(QuickSort)
欢迎来到繁星的CSDN,本期内容包括快速排序(QuickSort)的递归版本和非递归版本以及优化。

一、快速排序的来历
快速排序又称Hoare排序,由霍尔 (Sir Charles Antony Richard Hoare) ,一位英国计算机科学家发明。霍尔本人是在发现冒泡排序不够快的前提下,发明了快速排序。不像希尔排序等用名字命名排序方法,霍尔直接将其命名为快速排序,但时至今日,快速排序仍然是使用最广泛最稳定的排序算法。
二、快速排序主代码
快速排序是如何实现的呢?私以为思想和二叉树的前序遍历类似。
(没有看过二叉树的看这里:一文带你入门二叉树!-CSDN博客)
void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}快速排序采用了分治的思想,之前在排序(一)提到过,如果将数组拆成一个个小块再排序,会比一整个数组集体排序来的快。快排也正是利用这一点,从零到整地排序整个数组,并确定好分拆端点的最终位置,使得每一组的排序结束都是最终位置,无需再调整。而由于不知道数组需要被拆分成几块,类似于二叉树的递归遍历,快排也需要递归来帮助拆分和子数组排序。
下面阐述PartSort1这个函数是如何进行单趟排序的了。
三、快速排序(递归版单趟排序)
Part1 Hoare法
先上动图:

可以注意到,PartSort的参数是数组a,数组最左端元素的下标left,最右端元素的下标right。
key就是子数组(即left~right范围内)的第一个元素。
整个流程如下:
1、right向左遍历,直到找到一个小于key的值,停下。
2、left向右遍历,直到找到一个大于key的值,停下。
3、两者交换。
4、重复上述流程,直到left与right相遇,交换key和最后相遇处的下标mid。
5、随后返回mid,并利用mid继续将[left,right]区间分割为[left,mid-1]和[mid+1,right]区间,当不能分割的时候,该数组排序完毕。
问题讲解
如何确保key交换后所在的位置就是最终位置?
首先,从一个升序数组来看,对于其中任何一个元素(除首尾两个),该元素左侧均更小,右侧均更大。换句话说,保证左侧比key元素更小,右侧比key元素更大,即得到了这一元素的位置。
不难发现,被left遍历过的地址都是比key小的,被right遍历过的地址都是比key大的,因为如有left发现比key大,或者right发现比key小,都已进行过交换。
唯一需要判定的,就是最后一个元素是否比key小。
(1)left遇到right
当right停下,说明right所处位置的元素应该比key小。
那么left撞到right的时候,一定是right所处的位置,保证了该位置比key小。
(2)right遇到left
当left停下,说明已经交换完毕,此时left所处位置的元素比key小。
两种情况本质相同,都是保证了停下的那一方所处位置比key小。
int PartSort1(int* arr, int begin, int end)
{int left = begin, right = end;int key = begin;while (left < right){//left<right防止越界//使用>=而不是>防止数据出现死循环while (left < right && arr[right] >= arr[key])//寻找比key小的值{right--;}while (left < right && arr[left] <= arr[key])//寻找比key大的值{left++;}swap(&arr[left], &arr[right]);}int mid = left;swap(&arr[key], &arr[mid]);return mid;
}Part2 挖坑法
先上动图: 
挖坑法和hoare法的差别不大,思路都是将key的位置安排在最终位置后,再分段快排。
但挖坑法的确会比hoare法更加容易理解。
坑的位置就代表相遇位置,每“交换”一次,就将坑位换到被交换的位置,最后坑落在哪里,就将key值填入。
和hoare法不同的是,挖坑法需要多一个临时变量储存key值,在进行操作的时候只需要赋值,而不是swap交换。
int PartSort2(int* a, int left, int right) {int key = a[left];int hole = left;while (left < right) {while (left < right && a[right] >= key) {right--;}swap(&a[right], &a[hole]);hole = right;while (left < right && a[left] <= key) {left++;}swap(&a[left], &a[hole]);hole = left;}int mid = hole;a[hole] = key;return mid;
}Part3 双指针法
怎么能够让双指针缺席呢!

本质和前面两种没有区别,只是遍历的方向不同,前两种都是左右两侧开始遍历,而双指针法从一端开始遍历。prev代表比key小的值,cur去遍历,并确保prev的下一个位置上比key大,将较大的元素集体向后驱赶。
int PartSort3(int* a, int left, int right) {int fast = left;int slow = left;int key = a[left];while (fast <= right) {if(a[fast] < key)swap(&a[++slow], &a[fast]);fast++;}swap(&a[slow], &a[left]);return slow;
}总结
Part123三种办法没有高下之分,都可以作为QuickSort的一部分使用。
可以说QuickSort的代码实现和理解复杂程度并不如之前说的堆排那么抽象,但是性能确实优秀。
四、快速排序(非递归版)
我们知道,递归占据了大量的栈帧空间,尽管市面上大部分编译器已经增强了递归的性能,致使用递归的快排和不用递归的快排时间上差别不大,但递归空间上的占据却不可忽视。快排非递归版应运而生。
这一部分需要用到栈的知识,如果还没看,可以查看:栈和队列的介绍与实现-CSDN博客
非递归版本最重要的是,如何实现数组的分割,与进行多次排序。
利用好之前学过的数据结构,我们可以想起栈与队列,我们用栈来演示。
void QuickSortno(int* a, int left, int right) {Stack ps;StackInit(&ps);StackPush(&ps, left);StackPush(&ps, right);while (!StackEmpty(&ps)) {int end = StackTop(&ps);StackPop(&ps);int begin = StackTop(&ps);StackPop(&ps);int key=PartSort1(a, begin, end);if (key + 1 < end) {StackPush(&ps, key+1);StackPush(&ps, end);}if (key - 1 > begin) {StackPush(&ps, begin);StackPush(&ps, key-1);}}StackDestroy(&ps);
}有点像层序遍历,我们将待排序的子数组的两端,放入栈中,每两个为一组弹出并进行单趟排序,排序完毕后,将新增的两个子数组的两端放入栈中。循环往复,便可以得到结果。
本质思想还是一致的。
五、快速排序的优化
快速排序的最坏情况是升序/降序的数组,复杂度都达到了O(n^2)。
经研究表明,问题出在基准值上,也就是每次排序时最左端的数据。如果将基准值改为数组内的随机值,平均情况将比最好情况只糟39%,比只取最左端数据为基准值要好很多。
所以优化的第一个方向在于调整基准值。
三数取中法
int GetMidi(int* a, int left, int right)
{int midi = (left + right) / 2;// left midi rightif (a[left] < a[midi]){if (a[midi] < a[right]){return midi;}else if (a[left] < a[right]){return right;}else{return left;}}else // a[left] > a[midi]{if (a[midi] > a[right]){return midi;}else if (a[left] < a[right]){return left;}else{return right;}}
}代码很长,实际作用就是在left,(left+right)/2,right三个数中间取中间数,很好地做了分割。正如之前所述,越能将数组分割为两半,便越可以以更高的效率去排序。
小区间优化
优化的第二个方向在于快排的最后几层递归上。
无论递归多少次,我们都要在最后几层递归上耗费大量的时间与空间(只需要看区间数量,便可以知道需排序的区间呈指数级增长)。
递归是大招,但是更适合大场面,所以我们有以下优化:
if (left >= right)return;↓
if (right-left<=10)
{InsertSort(a+left, right - left+1);return;
}没错,就如排序(一)中提到的,如果数组元素比较少,插入排序的复杂度体现不出来。
这意味着我们可以在这个时候直接使用插入排序(当然希尔排序也是可以的,可为什么不全部都直接用希尔排序呢?)
感受一下优化过的和未优化过的:
优化前:

优化后:
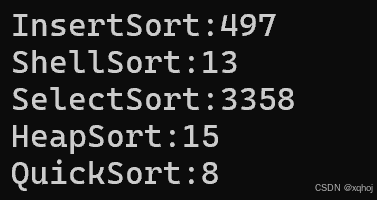
在10w量级的数据里,优化前后效率提升显著,相信量级更大的时候会更体现出优势。
本篇内容到此结束,谢谢大家的观看!
觉得写的还不错的可以点点关注,收藏和赞,一键三连。
我们下期再见~
往期栏目: 排序(一)——冒泡排序、直接插入排序、希尔排序(BubbleSOrt,InsertSort,ShellSort)-CSDN博客
相关文章:

排序(二)——快速排序(QuickSort)
欢迎来到繁星的CSDN,本期内容包括快速排序(QuickSort)的递归版本和非递归版本以及优化。 一、快速排序的来历 快速排序又称Hoare排序,由霍尔 (Sir Charles Antony Richard Hoare) ,一位英国计算机科学家发明。霍尔本人是在发现冒泡排序不够快…...
<数据集>穿越火线cf人物识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:3440张 标注数量(xml文件个数):3440 标注数量(txt文件个数):3440 标注类别数:1 标注类别名称:[person] 使用标注工具:labelImg 标注规则:对…...

a+=1和a=a+1的区别
文章目录 a1 和a a1的区别一、实例代码二、代码解释三、总结 a1 和a a1的区别 一、实例代码 public class Test {public static void main(String[] args) {byte a 10; // a a 1; // a (byte) (a 1);a 1;System.out.println(a);} }上面的对变量a进行加一操作时&a…...
)
设计模式使用场景实现示例及优缺点(结构型模式——桥接模式)
结构型模式 桥接模式(Bridge Pattern) 桥接模式(Bridge Pattern)是一种结构型设计模式,其主要目的是“将抽象与实现解耦,使得两者可以独立地变化”。这种模式通过提供抽象化和实现化之间的桥接结构&#…...

Spring——自动装配Bean
自动装配是Spring满足bean依赖的一种方式 Spring会在上下文中自动寻找,并自动给bean装配属性 在Spring中有三种装配的方式: 1. 在xml中显示配置 2. 在java中显示配置 3. 隐式的自动装配bean【重要】 测试 记得创建Cat、Dog、People类 public clas…...

云端典藏:iCloud中个人收藏品目录的智能存储方案
云端典藏:iCloud中个人收藏品目录的智能存储方案 在数字化生活不断推进的今天,个人收藏品的管理也趋向于电子化和云端化。iCloud作为苹果公司提供的云服务,为个人收藏品目录的存储和管理提供了一个安全、便捷、跨设备的解决方案。本文将详细…...

安全开发基础篇-数据溢出
上一节我们简单讲解了多语言的数据类型,我们只需要知道这个概念,并且在不同语言有不同的规矩就好。这节讲数据溢出,严格说应该是字符串溢出和整数溢出。 在软件开发中,字符串和整数溢出漏洞是常见的安全问题,它们可能…...

Scanner工具类
扫描控制台输入 1.nextLine nextLine() 方法会扫描输入流中的字符,直到遇到行末尾的换行符 \n,然后将该行的内容作为字符串返回,同时,nextLine() 会将 Scanner 对象的位置移动到下一行的开头,以便下一次读取数据时从下…...

springboot3 集成GraalVM
目录 安装GraalVM 配置环境变量 Pom.xml 配置 build包 测试 安装GraalVM Download GraalVM 版本和JDK需要自己选择 配置环境变量 Jave_home 和 path 设置setting.xml <profile><id>graalvm-ce-dev</id><repositories><repository><id&…...
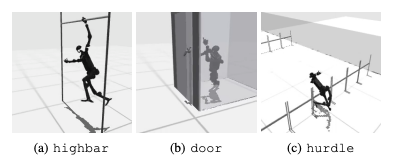
HumanoidBench——模拟仿人机器人算法有未来
概述 论文地址:https://arxiv.org/pdf/2403.10506 仿人机器人具有类似人类的外形,有望在各种环境和任务中为人类提供支持。然而,昂贵且易碎的硬件是这项研究面临的挑战。因此,本研究开发了使用先进模拟技术的 HumanoidBench。该基…...
)
实现前端用户密码重置功能(有源码)
引言 密码重置功能是任何Web应用程序中至关重要的一部分。当用户忘记密码时,密码重置功能可以帮助他们安全地重设密码。本文将介绍如何使用HTML、CSS和JavaScript(包括Vue.js)来实现前端的密码重置功能。 1. 项目结构 首先,我们…...

《双流多依赖图神经网络实现精确的癌症生存分析》| 文献速递-基于深度学习的多模态数据分析与生存分析
Title 题目 Dual-stream multi-dependency graph neural network enables precise cancer survival analysis 《双流多依赖图神经网络实现精确的癌症生存分析》 01 文献速递介绍 癌症是全球主要的死亡原因,2020年约有1930万新发癌症病例和近1000万癌症相关死亡…...

【Hive SQL 每日一题】在线峰值人数计算
文章目录 测试数据需求说明需求实现 测试数据 -- 创建 user_activity 表 DROP TABLE IF EXISTS user_activity ; CREATE TABLE user_activity (user_id STRING,activity_start TIMESTAMP,activity_end TIMESTAMP );-- 插入数据 INSERT INTO user_activity VALUES (user1, 2024…...

谷粒商城学习笔记-18-快速开发-配置测试微服务基本CRUD功能
文章目录 一,product模块整合mybatis-plus1,引入依赖2,product启动类指定mapper所在包3,在配置文件配置数据库连接信息4,在配置文件中配置mapper.xml映射文件信息 二,单元测试1,编写测试代码&am…...

机器学习库实战:DL4J与Weka在Java中的应用
机器学习是当今技术领域的热门话题,而Java作为一门广泛使用的编程语言,也有许多强大的机器学习库可供选择。本文将深入探讨两个流行的Java机器学习库:Deeplearning4j(DL4J)和Weka,并通过详细的代码示例帮助…...

MongoDB教程(一):Linux系统安装mongoDB详细教程
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 文章目录 引言一、Ubuntu…...

leetcode74. 搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非严格递增顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。…...

Redis 布隆过滤器性能对比分析
redis 实现布隆过滤器实现方法: 1、redis 的 setbit 和 getbit 特点:对于某个bit 设置0或1,对于大量的值需要存储,非常节省空间,查询速度极快,但是不能查询整个key所有的bit,在一次请求有大量…...

Java List不同实现类的对比
List不同实现类的对比 文章目录 List不同实现类的对比实现类之一ArrayList实现类之二 LinkedList实现类之三 Vector练习 java.util.Collection用于存储一个一个数据的框架子接口:List存储有序的、可重复的数据(相当于动态数组) ArrayList lis…...

【C语言】 —— 预处理详解(下)
【C语言】 —— 预处理详解(下) 前言七、# 和 \##7.1 # 运算符7.2 ## 运算符 八、命名约定九、# u n d e f undef undef十、命令行定义十一、条件编译11.1、单分支的条件编译11.2、多分支的条件编译11.3、判断是否被定义11.4、嵌套指令 十二、头文件的包…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
