【LeetCode】快乐数
目录
- 一、题目
- 二、解法
- 完整代码
一、题目
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
1 <= n <= 231 - 1
二、解法
简单粗暴的解法,模拟,将出现过的数字放入set中,如果遇到重复的了,就直接返回False为了防止绕圈
完整代码
class Solution:def isHappy(self, n: int) -> bool:man = nst = set()while man not in st:st.add(man)if man == 1:return Trueelse:new_man = 0while man != 0:tmp = man % 10man //= 10new_man += tmp * tmpman = new_manreturn False
相关文章:

【LeetCode】快乐数
目录 一、题目二、解法完整代码 一、题目 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变…...

大模型未来发展深度分析
大模型未来发展方向的深度探讨 近年来,人工智能技术的飞速发展,特别是大模型技术的崛起,为全球科技产业带来了前所未有的变革。大模型,以其强大的推理能力、创意生成能力和情绪智能,正在逐步成为推动社会经济发展的核…...
[线性RNN系列] Mamba: S4史诗级升级
前言 iclr24终于可以在openreview上看预印本了 这篇(可能是颠覆之作)文风一眼c re组出品;效果实在太惊艳了,实验相当完善,忍不住写一篇解读分享分享。 TL;DR (overview) Structured State-Sp…...

【鸿蒙学习笔记】元服务
官方文档:元服务规格 目录标题 什么是元服务特征第一个元服务-案例介绍创建项目源码启动模拟器启动entry创建卡片出发元服务 什么是元服务 特征 免安装分包预加载老化和更新机制 第一个元服务-案例介绍 创建项目 源码 Entry Component struct WidgetCard {buil…...

LIS+找规律,CF 582B - Once Again...
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 582B - Once Again... 二、解题报告 1、思路分析 考虑朴素做法对T *n的数组求LIS 但是T * n可达1e9 思考一下,最优解无非就是几个循环节拼接,我们最差情况下对sqrt(T)个a[]求LIS即…...
——开发:数据拆分——实施过程、应用特点)
数据赋能(145)——开发:数据拆分——实施过程、应用特点
实施过程 数据拆分的实施过程通常涉及以下几个关键步骤: 确定拆分目标和需求: 明确数据拆分的目的和需求,例如是为了减少数据处理的复杂性、提高查询效率还是为了满足特定的业务需求。根据需求确定拆分后的数据结构和拆分规则。选择拆分方法…...

【漏洞复现】Splunk Enterprise for Windows 任意文件读取漏洞 CVE-2024-36991
声明:本文档或演示材料仅用于教育和教学目的。如果任何个人或组织利用本文档中的信息进行非法活动,将与本文档的作者或发布者无关。 一、漏洞描述 Splunk Enterprise 是一款强大的机器数据管理和分析平台,广泛应用于企业中,用于实…...

FastAPI -- 第一弹
Hello World 经典的 Hello World 安装 pip install fastapi pip install "uvicorn[standard]"main.py from typing import Unionfrom fastapi import FastAPIapp FastAPI()app.get("/") def read_root():return {"Hello": "World"}…...

C++入门基础篇(1)
欢迎大家来到海盗猫鸥的博客—— 断更许久,让我们继续好好学习吧! 目录 1.namespace命名空间 命名空间的存在价值: 命名空间的定义: 命名空间的使用: 2.C输入输出函数 使用: 3.缺省参数 4.函数重载…...

基于html开发的在线网址导航在线工具箱源码
基于html开发的在线网址导航在线工具箱源码,将全部文件复制到服务器,入口文件是index.html 如需修改网址,可修改index.html 如需修改关于页面,可修改about里面的index页面 源码下载:https://download.csdn.net/down…...

【密码学】大整数分解问题和离散对数问题
公钥密码体制的主要思想是通过一种非对称性,即正向计算简单,逆向计算复杂的加密算法设计,来解决安全通信。本文介绍两种在密码学领域内最为人所熟知、应用最为广泛的数学难题——大整数分解问题与离散对数问题 一、大整数分解问题 …...

解析 pdfminer layout.py LAParams类及其应用实例
解析 pdfminer layout.py LAParams类及其应用实例 引言类的定义1. line_overlap2. char_margin3. word_margin4. line_margin5. boxes_flow6. detect_vertical7. all_texts 类的初始化参数验证类的表示总结 引言 在这篇文章中,我们将解析一个叫做 LAParams 的类。这…...

Redis官方可视化管理工具
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl RedisInsight是一个Redis可视化工具,提供设计、开发和优化 Redis 应用程序的功能。RedisInsight分为免费的社区版和一个付费的企业版,免费版具有基本…...

android 固定图片大小
在Android中,固定图片大小可以通过多种方法实现,这些方法主要涉及到ImageView控件的使用、Bitmap类的操作,以及第三方库(如Glide)的辅助。以下是几种常见的方法: 1. 使用ImageView控件 在Android的布局文…...

操作系统——内存管理(面试准备)
虚拟内存 单片机没有操作系统,每次写完代码,都需要借助工具把程序烧录进去,这样程序才能跑起来。 另外,单片机的CPU是直接操作内存的物理地址。 在这种情况下,想在内存中同时运行两个程序是不可能的,如果第…...

vue3实现vuedraggable实现拖拽到垃圾桶图标位置进行删除
当使用Vue 3和vuedraggable库时,你可以按照以下方式实现拖拽到垃圾桶图标位置进行删除的功能: 首先,确保你已经安装了vuedraggable库。如果没有安装,可以通过以下命令进行安装: vuedraggable 和vue-draggable-plus使…...

MySQL向自增列插入0失败问题
问题 在一次上线时,发现通过脚本添加的状态表中,待提交的状态不正确,本来应该是0,线上是101。 原因 默认情况下,MySQL对应自增列,认为0和null等价(因为mysql认为0不是最佳实践不推荐使用&…...
Python:Python基础知识(注释、命名、数据类型、运算符)
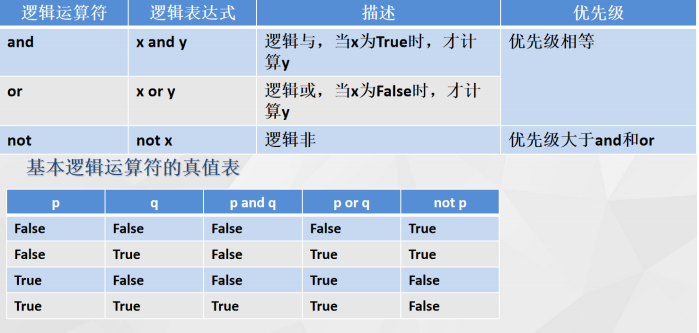
.注释 Python有两种注释方法:单行注释和多行注释。单行注释以#开头,多行注释以三个单引号 或三个双引号 """ 开头和结尾。 2.命名规则 命名规则: 大小写字母、数字、下划线和汉字等字符及组合; 注意事项: 大小写敏感、首…...
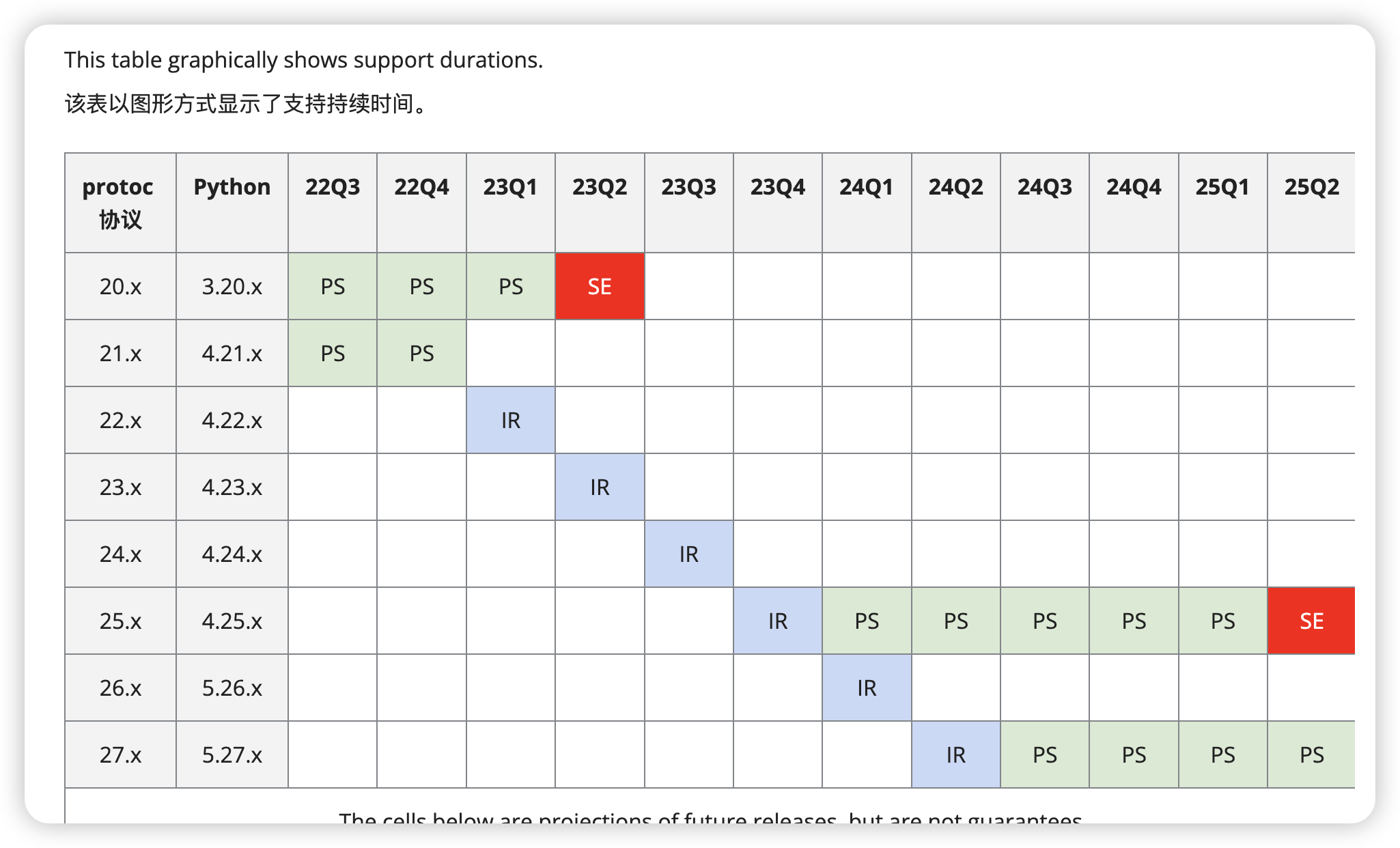
Protobuf: 大数据开发中的高效数据传输利器
作为一名大数据开发者,我经常需要处理海量的数据传输和存储。在这个过程中,选择一个高效、可靠的数据序列化工具至关重要。今天,我想和大家分享一下我在项目中使用 Protobuf 的经历。 目录 故事背景Protobuf 简介优点: 实战案例示…...

MySQL 面试相关问题
写在前面: 不喜勿喷,暴躁作者又不求你给钱【没办法,遇见的狗喷子太多了🐶】欢迎大家在评论区留言,指正文章中的信息错误有一些其他相关的问题,可以直接评论区留言,作者看到会及时更新到文章末尾…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
