【密码学】大整数分解问题和离散对数问题
公钥密码体制的主要思想是通过一种非对称性,即正向计算简单,逆向计算复杂的加密算法设计,来解决安全通信。本文介绍两种在密码学领域内最为人所熟知、应用最为广泛的数学难题——大整数分解问题与离散对数问题
一、大整数分解问题
(1)问题的定义
假设 𝑁 是一个合数,且 𝑁=𝑝×𝑞,其中 𝑝 和 𝑞 都是大于1的大质数(又叫素数)。大整数分解问题的目标是,仅给定 𝑁,找到 𝑝 和 𝑞。更一般地,问题是找到所有质数因子,而不仅仅局限于两个因子的情况。
【注】质数(Prime Number)是指在大于1的自然数中,除了1和它本身以外不再有其他因数的数。换句话说,质数只能被1和它自身整除。例如,2、3、5、7、11、13等都是质数。
(2)非对称性的体现
- 正向计算容易:找到两个大素数并计算它们的乘积是非常简单的。现代计算机可以迅速地找到这样的素数并对它们执行乘法操作。
- 逆向计算困难:然而,给定𝑛来找出它的两个素数因子𝑝和𝑞是非常困难的。随着𝑛的位数增加,分解𝑛所需的计算资源呈指数级增长。当前的算法,在分解大整数时需要耗费大量的时间和计算能力,这使得在合理的时间内分解大整数变得不切实际。
(3)密钥生成与加解密简述
① 密钥生成算法
随机选择两个大素数p和q;计算;计算欧拉函数
;选择一个整数e,使得1 < e < φ(N),且e与φ(N)互质;计算d作为e关于φ(N)的模逆元,即找到d满足de ≡ 1 (mod φ(N));
- 公钥是(N, e),其中N是模数,e是加密指数;
- 私钥是(d, N),其中d是解密指数,N同样是模数。
② 加密算法
发送方使用接收方的公钥对明文
进行加密,生成密文
加密过程通常表示为
③ 解密算法
接收方使用自己的私钥对密文
进行解密,恢复出明文
解密过程表示为

二、离散对数问题
(1)问题的定义
给定一个有限域 G,以及该域中的一个生成元(或称为基)一个元素
,离散对数问题可以这样表述:
对于任意给定的G中的非零元素,找到一个整数,使得
的
次方模上
等于
,即
如果这样的 存在,则称
为
相对于基
的离散对数。这里的“离散”一词,是因为群G通常是一个离散集合,而不是连续的。
【注】G称为模 𝑝 的有限域,其中 𝑝 必须是一个素数。这样所有加法、减法、乘法和除法运算的结果都会被取模 𝑝 来确保结果仍然在这个有限域内。
有关离散对数更直观的介绍可以去看可汗学院的视频:The discrete logarithm problem
也有国内搬运的版本:什么是离散的对数问题?
(2)非对称性的体现
- 正向计算容易:计算
是非常直接且快速的,可以通过快速幂算法在多项式时间内完成。
- 逆向计算困难:然而,给定𝑔和𝑦,找到𝑥是非常困难的,特别是在𝑝非常大的情况下。目前没有已知的多项式时间算法能够解决这个问题,尽管存在一些算法可以优化搜索过程,但当𝑝足够大时,这些算法仍然需要指数级的时间。
(3)密钥生成与加解密简述
① 密钥生成算法
以ElGamal加密算法为例。
-
选择一个大素数 p 、一个原根 g 和模 p。原根意味着 g 的所有幂次模 p 将遍历所有非零的模 p 的剩余类。
-
选择私钥
,这是一个小于
的随机整数。
-
计算公钥
,其中
。
公钥是,而私钥是
② 加密算法
假设 Alice 想要向 Bob 发送一条消息 ,并且 Bob 的公钥是
:
-
选择一个随机数 𝑘,其中 1<𝑘<𝑝−1
-
计算第一个加密分量
-
计算第二个加密分量
加密后的消息是
③ 解密算法
Bob 收到加密消息后,使用他的私钥
来解密:
-
计算中间值
-
计算消息
这里的 是指 𝑠 在模 𝑝 下的乘法逆元,也就是说,找到一个数 𝑧,使得

相关文章:

【密码学】大整数分解问题和离散对数问题
公钥密码体制的主要思想是通过一种非对称性,即正向计算简单,逆向计算复杂的加密算法设计,来解决安全通信。本文介绍两种在密码学领域内最为人所熟知、应用最为广泛的数学难题——大整数分解问题与离散对数问题 一、大整数分解问题 …...

解析 pdfminer layout.py LAParams类及其应用实例
解析 pdfminer layout.py LAParams类及其应用实例 引言类的定义1. line_overlap2. char_margin3. word_margin4. line_margin5. boxes_flow6. detect_vertical7. all_texts 类的初始化参数验证类的表示总结 引言 在这篇文章中,我们将解析一个叫做 LAParams 的类。这…...

Redis官方可视化管理工具
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl RedisInsight是一个Redis可视化工具,提供设计、开发和优化 Redis 应用程序的功能。RedisInsight分为免费的社区版和一个付费的企业版,免费版具有基本…...

android 固定图片大小
在Android中,固定图片大小可以通过多种方法实现,这些方法主要涉及到ImageView控件的使用、Bitmap类的操作,以及第三方库(如Glide)的辅助。以下是几种常见的方法: 1. 使用ImageView控件 在Android的布局文…...

操作系统——内存管理(面试准备)
虚拟内存 单片机没有操作系统,每次写完代码,都需要借助工具把程序烧录进去,这样程序才能跑起来。 另外,单片机的CPU是直接操作内存的物理地址。 在这种情况下,想在内存中同时运行两个程序是不可能的,如果第…...

vue3实现vuedraggable实现拖拽到垃圾桶图标位置进行删除
当使用Vue 3和vuedraggable库时,你可以按照以下方式实现拖拽到垃圾桶图标位置进行删除的功能: 首先,确保你已经安装了vuedraggable库。如果没有安装,可以通过以下命令进行安装: vuedraggable 和vue-draggable-plus使…...

MySQL向自增列插入0失败问题
问题 在一次上线时,发现通过脚本添加的状态表中,待提交的状态不正确,本来应该是0,线上是101。 原因 默认情况下,MySQL对应自增列,认为0和null等价(因为mysql认为0不是最佳实践不推荐使用&…...
Python:Python基础知识(注释、命名、数据类型、运算符)
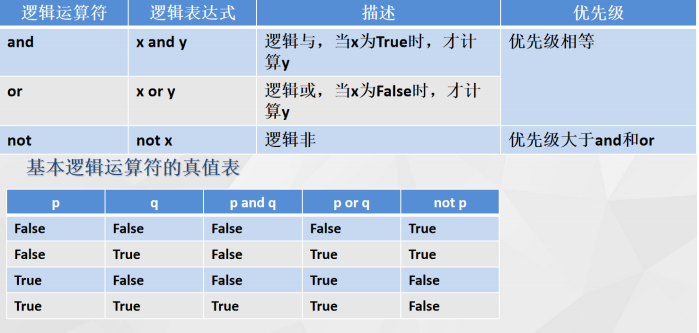
.注释 Python有两种注释方法:单行注释和多行注释。单行注释以#开头,多行注释以三个单引号 或三个双引号 """ 开头和结尾。 2.命名规则 命名规则: 大小写字母、数字、下划线和汉字等字符及组合; 注意事项: 大小写敏感、首…...
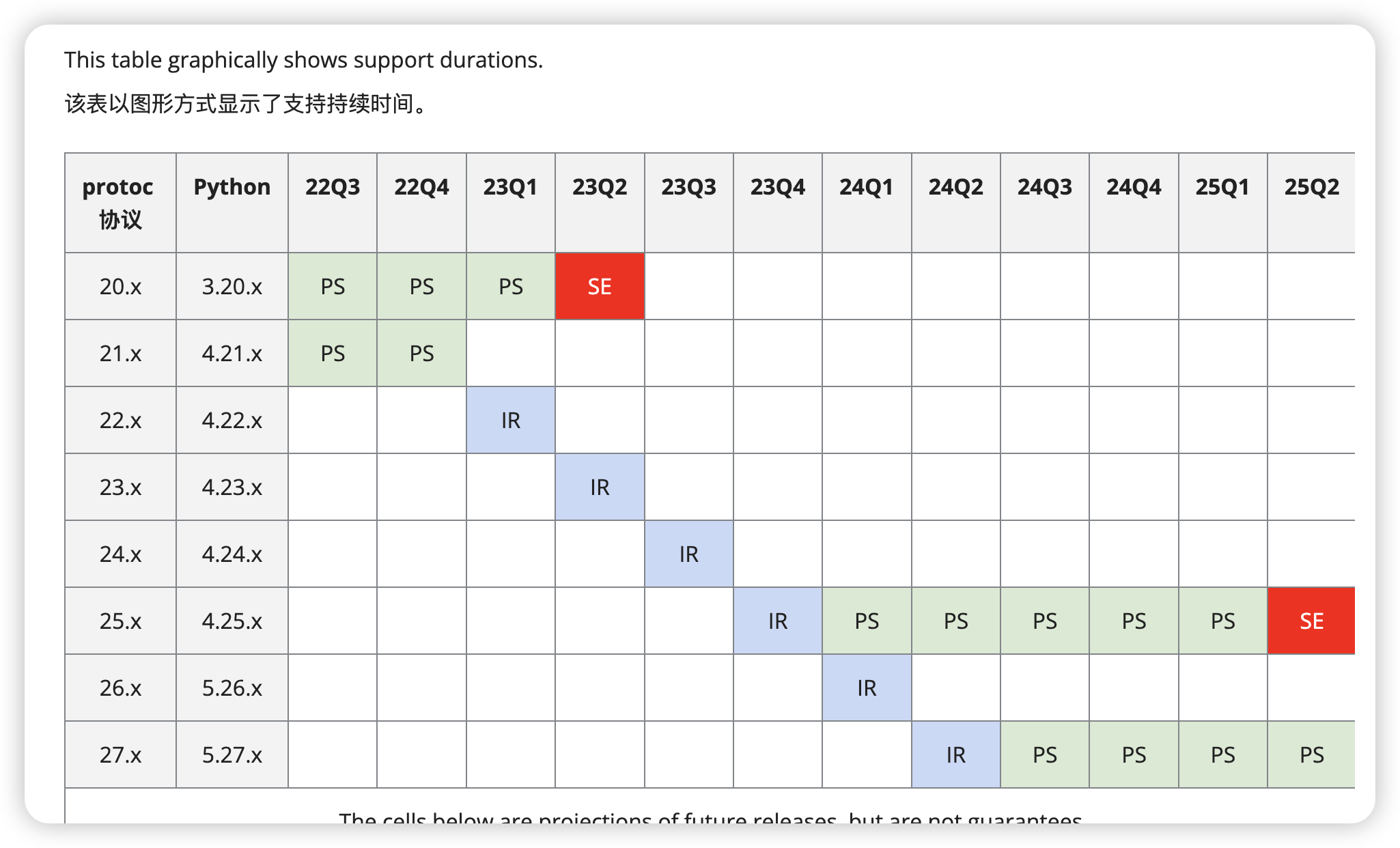
Protobuf: 大数据开发中的高效数据传输利器
作为一名大数据开发者,我经常需要处理海量的数据传输和存储。在这个过程中,选择一个高效、可靠的数据序列化工具至关重要。今天,我想和大家分享一下我在项目中使用 Protobuf 的经历。 目录 故事背景Protobuf 简介优点: 实战案例示…...

MySQL 面试相关问题
写在前面: 不喜勿喷,暴躁作者又不求你给钱【没办法,遇见的狗喷子太多了🐶】欢迎大家在评论区留言,指正文章中的信息错误有一些其他相关的问题,可以直接评论区留言,作者看到会及时更新到文章末尾…...

java org.aeonbits.owner库介绍
org.aeonbits.owner 是一个用于简化Java应用程序配置管理的库。它通过使用接口和注解来定义和读取配置,使得配置管理更加简洁和类型安全。以下是对这个库的一些主要特性和功能的介绍: 主要特性 类型安全的配置: OWNER 库允许开发者使用接口定义配置,从而提供了编译时的类型…...
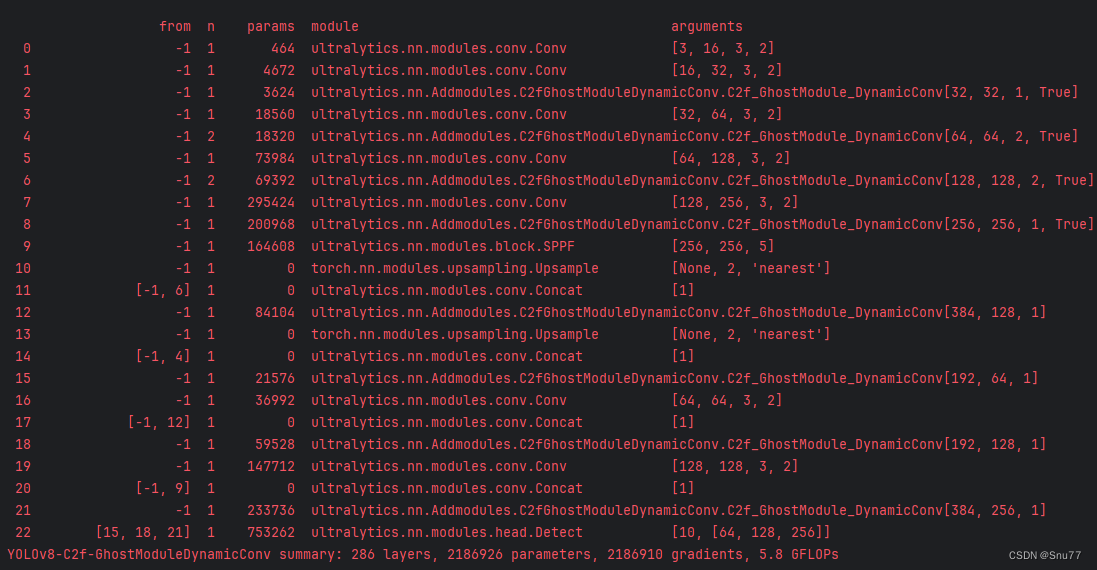
YOLOv10改进 | 添加注意力机制篇 | 添加LSKAttention大核注意力机制助力极限涨点
一、本文介绍 在这篇文章中,我们将讲解如何将LSKAttention大核注意力机制应用于YOLOv10,以实现显著的性能提升。首先,我们介绍LSKAttention机制的基本原理,它主要通过将深度卷积层的2D卷积核分解为水平和垂直1D卷积核࿰…...

学习笔记——动态路由——IS-IS中间系统到中间系统(特性之路由撤销)
6、路由撤销 ISIS路由协议的路由信息是封装在LSP报文中的TLV中的,但是它对撤销路由的处理和OSPF的处理方式类似。 在ISIS中撤销一条路由实则是将接口下的ISIS关闭: 撤销内部路由: 在ISIS中路由信息是由IP接口TLV和IP内部可达性TLV共同来描…...
)
智能无人机控制:STM32微控制器与机器学习集成(内附资料)
智能无人机控制结合了STM32微控制器的实时处理能力和机器学习算法的决策能力,以实现更高级的自主飞行和任务执行。以下是智能无人机控制系统的概述,包括系统架构、关键组件、集成方法和示例代码。 系统概述 智能无人机控制系统利用STM32微控制器进行实…...

力扣 454四数相加
这个题给了四个数组,可以两两判断,就类比两数相加那道题了 对于num1 num2 用unordered_map存储,key是num1,num2中数字相加之和,value是值出现的次数 for(int a:num1) {for(int b:num2 {map[ab]; 最后要计算四个数…...

Java面试题系列 - 第9天
题目:深入探讨Java中的设计模式及其应用场景 背景说明:设计模式是软件工程中解决问题的常见方案,它们提供了经过验证的模板,帮助开发者解决在软件设计过程中遇到的特定问题。在Java中,熟悉并正确应用设计模式能够显著…...

数据结构【顺序表】
目录 线性表 顺序表 概念与结构 分类 静态顺序表 动态顺序表 动态顺序表的实现 在头文件中创建结构体 初始化顺序表 销毁顺序表(可以留到后面再看) 尾插数据 申请空间 打印顺序表数据 头插数据 尾删除数据 头删除数据 在指定位置插…...

【JavaScript 报错】未捕获的类型错误:Uncaught TypeError
🔥 个人主页:空白诗 文章目录 一、错误原因分析1. 调用不存在的方法2. 访问未定义的属性3. 数据类型不匹配4. 函数参数类型不匹配 二、解决方案1. 检查方法和属性是否存在2. 使用可选链操作符3. 数据类型验证4. 函数参数类型检查 三、实例讲解四、总结 在…...
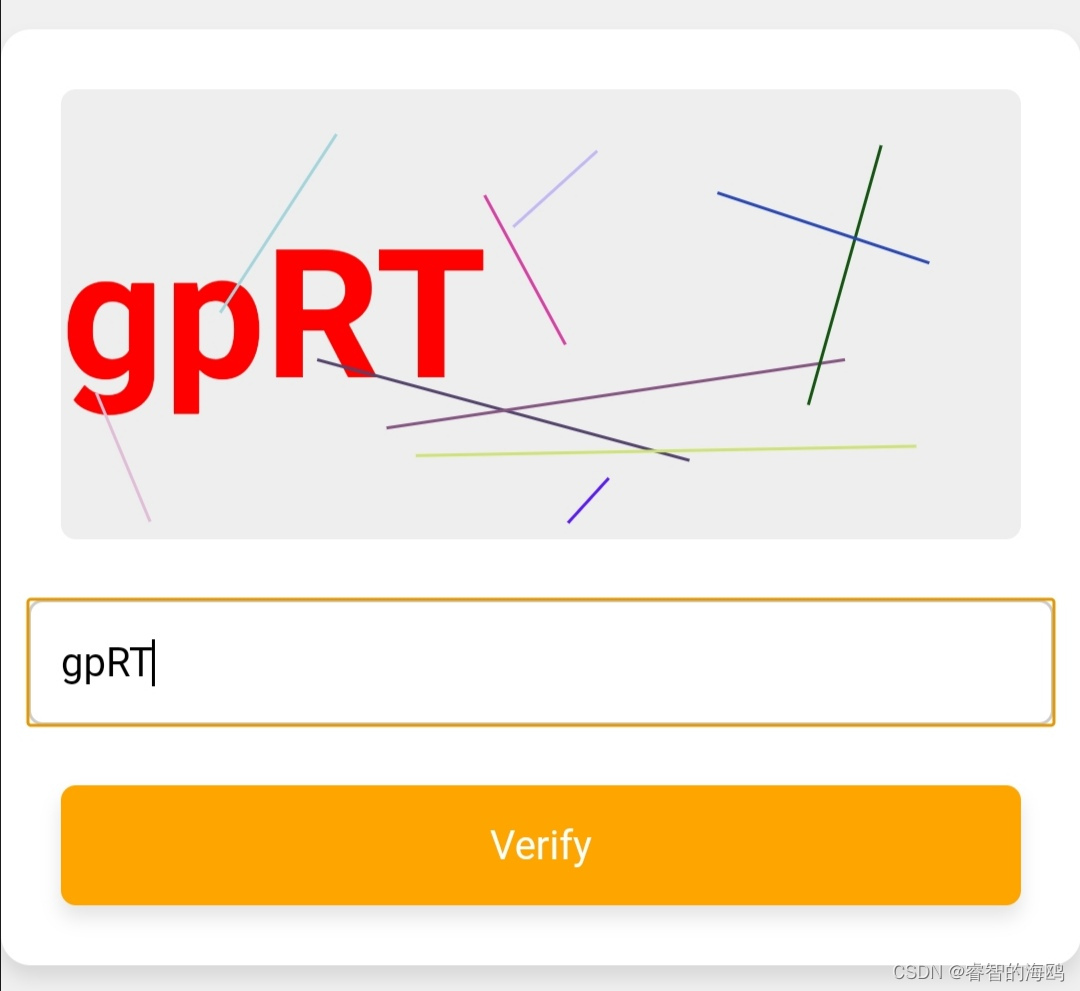
html+css+js随机验证码
随机画入字符、线条 源代码在图片后面 点赞❤️关注😍收藏⭐️ 互粉必回 图示 源代码 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"…...

WPS打开PDF文件的目录
WPS打开PDF文件的目录 其实WPS中PDF文件并没有像Word那样标准的目录,但是倒是有书签,和目录一个效果 点击左上角书签选项,或者使用Alt Shift 1快捷键即可...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
