递推(C语言)
文章目录
- 1.斐波那契数列
- 2.太波那契数列
- 3.二维递推问题
- 4.实战
- 4.1 力扣509 斐波那契数
- 4.2 力扣70 爬楼梯
- 4.3 力扣119 杨辉三角||
递推最通俗的理解就是数列,递推和数列的关系就好比 算法 和 数据结构 的关系,数列有点
像数据结构中的线性表(可以是顺序表,也可以是链表,一般情况下是顺序表),而递推就是一
个循环或者迭代的枚举过程。
递推本质上是数学问题,所以有同学问算法是不是需要数学非常好,也并不是,你会发现
这些数学只不过是初中高中我们学烂的东西,高考都经历了,这些东西又何足为惧!?
1.斐波那契数列
斐波那契数(通常用F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面
的每一项数字都是前面两项数字的和。也就是:
F(0)=0,F(1)=1
F(n)=F(n -1)+ F(n- 2),其中n>1,给定n(0 ≤n≤ 30),请计算 F(n)
拿到这个题目,我们首先来看题目范围,最多不超过 30,那是因为斐波那契数的增长速度很
快,是指数级别的。所以如果n 很大,就会超过 c语言 中32位整型的范围。这是一个最基础的递
推题,递推公式都已经告诉你了,我们要做的就是利用一个循环来实现这个递推。
我们只需要用一个 F[31]数组,初始化好 F[0]和 F[1],然后按照给定的公式循环计算就可以。
int febonacci(int n) { int F[30] = {0,1}; for (int i = 2; i < 30; i++) { F[i] = F[i - 1] + F[i - 2]; } return F[29]
}
2.太波那契数列
泰波那契序列Tn定义如下:
T(0) = 0, T(1) = 1,T(2)=1
且在 n>2的条件下 T(n)=T(n-1)+T(n-2)+T(n-3),给你整数n,请返回第n个泰波那契
数T(n)的值。
如果已经理解斐波那契数列,那么这个问题也不难,只不过初始化的时候,需要初始化前三个数,
并且在循环迭代计算的时候,当前数的值需要前三个数的值累加和。像这样:
int tribonacci(int n) { int F[30] = {0,1,1}; for (int i = 3; i < 30; i++) { F[i] = F[i - 1] = F[i - 2] + F[i - 3]; } return F[29];
}
3.二维递推问题
像斐波那契数列这种问题,是一个一维的数组来解决的,有些时候,一维解决不了的时候,我
们就需要升高一个维度来看问题了。
长度为n(1<n<40)的只由’A’、'C’、"M’三种字符组成的字符串(可以只有其中一种或两种字
但绝对不能有其他字符)且禁止出现 M 相邻的情况,问这样的串有多少种?
考虑长度为n,且以’A’ 结尾的串有f[n][0]种、以’C’ 结尾的串有f[n][1]种、以’’ 结尾的串有
f[n][2]种
4.实战
4.1 力扣509 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。
int fib(int n){if(n == 0){return 0;}else if (n == 1){return 1;}return fib(n - 1) + fib(n - 2);
}
4.2 力扣70 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
int climbStairs(int n) { int f[46]; f[0] = 1; f[1] = 1; for(int i = 2; i <= n; i++){ f[i] = f[i - 1] + f[i - 2]; } return f[n];
}
4.3 力扣119 杨辉三角||
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
int* getRow(int rowIndex, int* returnSize) { int f[34][34]; for(int i = 0; i <= rowIndex; i++){ for(int j = 0; j <= i; j++){ if(j ==0 || j == i){ f[i][j] = 1; } else { f[i][j] = f[i - 1][j] + f[i - 1][j - 1]; } } } int* ret = (int *)malloc (sizeof(int) * (rowIndex + 1)); for(int j = 0; j <= rowIndex; j++){ ret[j] = f[rowIndex][j]; } *returnSize = rowIndex + 1; return ret;
}
相关文章:
)
递推(C语言)
文章目录 1.斐波那契数列2.太波那契数列3.二维递推问题4.实战4.1 力扣509 斐波那契数4.2 力扣70 爬楼梯4.3 力扣119 杨辉三角|| 递推最通俗的理解就是数列,递推和数列的关系就好比 算法 和 数据结构 的关系,数列有点 像数据结构中的线性表(可以是顺序表&…...
安卓微信8.0之后如何利用缓存找回的三天之前不可见的朋友圈图片
安卓微信8.0之后如何利用缓存找回的三天之前不可见的朋友圈图片 复习了下安卓程序的知识,我们会了解到,安卓程序清楚数据的时候有两个选项 一个是清除全部数据一个是清除缓存。 清除全部数据表示清除应用数据缓存。 对于安卓微信8.0之后而言࿰…...
 总结(九))
ES6 Class(类) 总结(九)
ES6 中的 class 是一种面向对象编程的语法糖,提供了一种简洁的方式来定义对象的结构和行为。 JavaScript 语言中,生成实例对象的传统方法是通过构造函数。下面是一个例子。 function Point(x, y) {this.x x;this.y y; } Point.prototype.toString fu…...

使用 Vue.js 和 Element Plus 实现自动完成搜索功能
使用 Vue.js 和 Element Plus 实现自动完成搜索功能 一、前言1.环境准备2.组件配置3.后端数据请求4.样式5.总结 一、前言 在前端开发中,实现自动完成(autocomplete)功能可以极大地提升用户体验,特别是在需要用户输入和选择内容的…...

SpringBoot自定义starter
SpringBoot自定义starter 1、SpringBoot之starter机制 1.1、什么是自定义starter SpringBoot中的starter是一种非常重要的机制(自动化配置),能够抛弃以前繁杂的配置,将其统一集成进starter,应用者只需要在maven中引入starter依赖&#…...

深入探索大语言模型
深入探索大语言模型 引言 大语言模型(LLM)是现代人工智能领域中最为重要的突破之一。这些模型在自然语言处理(NLP)任务中展示了惊人的能力,从文本生成到问答系统,无所不包。本文将从多个角度全面介绍大语…...
)
querylist多线程采集curlMulti时,报错Curl error(60)
前言 在使用querylist多线程采集的时候,报错: Curl error(60)。测试了下用http时没有问题,https时有问题。其原因在于多线程采集库引用的另一个库有问题。需要手动更改。 解决 找到:vendor/ares333/php-curl/src/Curl.php 文件,…...

Python数据分析~~美食排行榜
目录 1.模块的导入和路径的选择 2.访问前面五行数据 3.按照条件进行筛选 4.获取店铺评分里面的最高分 5.打印对应的店铺的名字 1.模块的导入和路径的选择 # 导入pandas模块,简称为pd import pandas as pd # 使用read_csv()函数 # TODO 读取路径"/Users/fe…...

Linux下解压.tar.gz文件
.tar.gz 是一种常用的压缩包格式,尤其在Unix、Linux以及macOS系统中非常普遍。这个格式结合了两种不同的功能: Tar (.tar): “Tar” 是“Tape Archive”的缩写,最初是为了将数据备份到磁带上而设计的。Tar命令可以将多个文件和目录打包成一个…...

【电商选品干货】差异化卖点要这样打造,80%商家却做不到
今天就给大家说说,如何去挖掘产品的差异化卖点?我们要找差异化卖点,就是因为我们的产品转化率不足,通常有下面几点原因: 1、产品差异化卖点不足,商家占比30% 2、流量和产品卖点不匹配,商家占比…...

LabVIEW比例压力控制阀自动测试系统
开发了一套基于LabVIEW编程和PLC控制的比例控制阀自动测试系统。该系统能够实现共轨管稳定的超高压供给,自动完成比例压力控制阀的耐久测试、流量滞环测试及压力-流量测试。该系统操作简便,具有高精度和高可靠性,完全满足企业对自动化测试的需…...

运营商认证API在Java、Python、PHP中的使用教程
随着数字化浪潮的推进,实名认证已深入我们生活的方方面面,从线上购物到电子资金转移,手机号已成为注册账号的主要凭证。然而,这也带来了身份验证的难题和手机号被盗用注册账号的风险。在信息爆炸的时代背景下,确保每个…...

用虚拟机,可以在x86的电脑上虚拟出arm的电脑吗
1.用虚拟机,可以在x86的电脑上虚拟出arm的电脑吗 是的,可以在x86的电脑上使用虚拟机技术虚拟出ARM架构的电脑。以下是通过虚拟机实现x86电脑上虚拟ARM电脑的几个关键步骤: 选择合适的虚拟化软件:通常,你可以使用如QE…...

富格林:可信观念摆脱暗箱陷阱
富格林指出,投资者产生的暗箱亏损多半是由于被不可信观念的迷惑影响,以为真的可以毫不费力就能赚钱,最后发现连交易的本金都打水漂了。事实上,投资市场并不像大家想得那么简单。要想安全实现交易成功,避免暗箱陷阱&…...
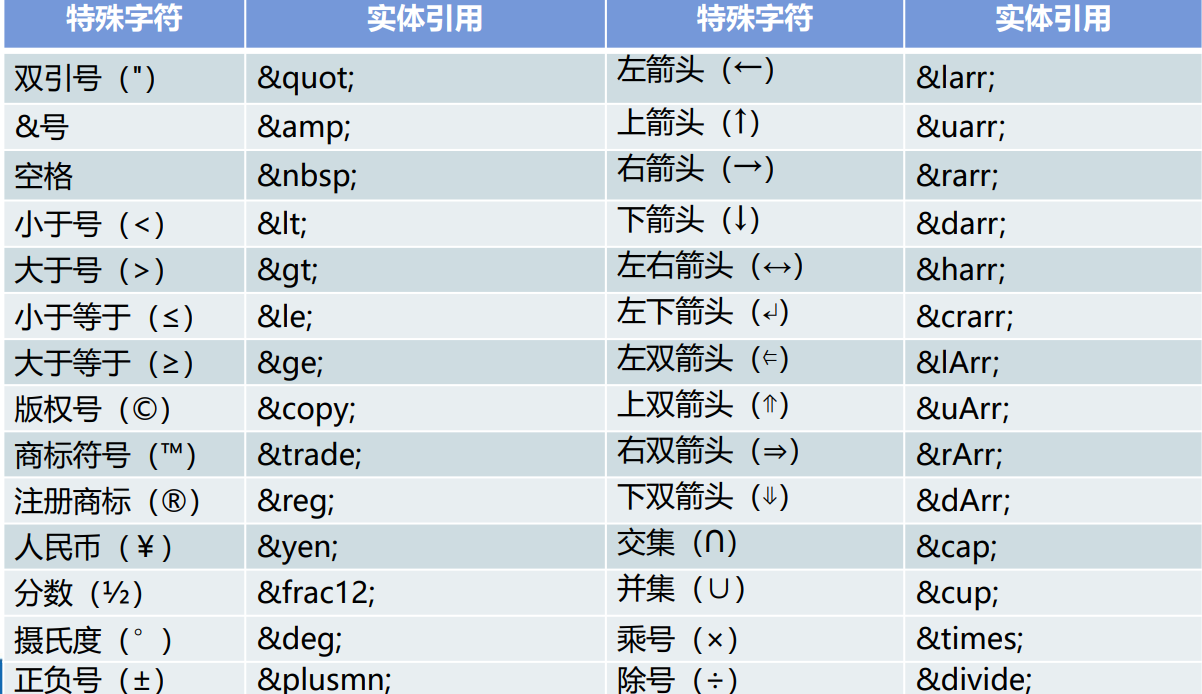
WEB前端01-HTML5基础(01)
一.WEB相关概念 软件架构 C/S: Client/Server (客户端/服务器端):在用户本地有一个客户端程序,在远程有一个服务器端程序 优点:用户体验好 缺点:开发、安装,部署,维护麻烦 B/S: Br…...

JUC-常见方法与线程的状态
常见方法 start()与run() 主线程直接调用某个线程t1的run()方法,run方法也会执行,但是并不会启动新的线程,而是有主线程调用的run方法,必须使用start才能启动新线程,但是start只能调用一次。 sleep()与yield() sle…...

如果你酿的酒是黄色,说明肯定是 “糊锅”了。
刚刚酿出的酒一般都是清澈见底的,如果你酿的酒是黄色,说明肯定是 “糊锅”了。这样的酒不仅颜色是黄的,而且还能闻到一股特别浓厚的 焦糊味。 这样的酒,米酒小哥是非常非常熟悉的,因为刚开始学习酿酒的那段时 间&#…...

国漫推荐07
玄幻、奇幻 1.侠岚系列 《侠岚》(第1至6季) 《画江湖之侠岚》(侠岚第7季) 2.《斗破苍穹》 三十年河东,三十年河西,莫欺少年穷! 3.《武动乾坤》(第1至4季) 4.《妖神记》…...

力扣刷题35.搜索查找位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出: 2示例 2: 输入:…...

setContentView 流程
setContentView 流程 Activity -> setContentView 开发者设置入口PhoneWindow -> setContentView mWindow 在 attach 时初始化为 PhoneWindow,同时PhoneWindow也是Window唯一的实现类PhoneWindow -> installDecor 这一步的作用是 初始化DecorView, 把Deco…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
